第23章 图形的相似 习题课件(共237张PPT) 2024-2025学年数学华东师大版九年级上册
文档属性
| 名称 | 第23章 图形的相似 习题课件(共237张PPT) 2024-2025学年数学华东师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 10:31:42 | ||
图片预览











文档简介
(共237张PPT)
第1课时 成比例线段
第23章 图形的相似
一、选择题
1.如果2a=-3b,那么=( B )
A.- B.- C.5 D.-1
2.下列线段的长度成比例的是( A )
A.1cm、2cm、3cm、6cm
B.2cm、3cm、4cm、5cm
C.1.5cm、2.5cm、4cm、5cm
D.1.1cm、2.2cm、3.3cm、4.4cm
B
A
3.若==(b+d≠0),则的值为( A )
A. B. C.1 D.
4.若a,b,c,d是成比例线段,其中a=3cm,c=6cm,d=4cm,则b的长为( D )
A.8cm B.cm C.4cm D.2cm
A
D
5.若==≠0,则下列各式正确的是( B )
A.2x=3y=4z B.=
C.= D.=
B
二、填空题
6.(1)已知一矩形的长a=1.35m,宽b=60cm,则a∶b= 9∶4 ;
(2)已知点P在线段AB上,且AP∶PB=2∶5,则AB∶PB= 7∶5 ,AP∶AB= 2∶7 .
9∶4
7∶5
2∶7
三、解答题
7.(1)求比例(1-2x)∶(5-x2)=2∶x中的x的值;
解:由比例的性质,得:x(1-2x)=2(5-x2),
∴x-2x2=10-2x2,
∴x=10.
(2)已知==2,求和的值;
解:∵==2,
∴a=2b,c=2d,
∴==,
==.
(3)已知线段a,b,c满足==,且a+2b+c=26.
①求a,b,c的值;
②若线段x是线段6a,b的比例中项,求x的值.
解:①设===k(k≠0),
则a=3k,b=2k,c=6k,
∵a+2b+c=26,
∴3k+2×2k+6k=26,解得k=2,
∴a=3×2=6,
b=2×2=4,
c=6×2=12;
②∵线段x是线段6a,b的比例中项,
∴x2=6ab=6×6×4=144,
∴x=12.
8.若点M在线段AB上,点N在线段BA的延长线上,AB=18,==,求线段MN的长.
解:根据题意画图得:
∵AB=18,==,
∴AM=AB=8,AN=4AB=72,
∴MN=AN+AM=80,
答:线段MN的长为80.
一、选择题
9.若三角形三边长之比为a∶b∶c=3∶4∶5,且a-b+c=12,则这个三角形的周长为( D )
A.12 B.18 C.24 D.36
D
二、填空题
10.正方形ABCD的两条对角线相交于点O,则AO∶AB∶AC= 1∶∶2 .
1∶∶2
三、解答题
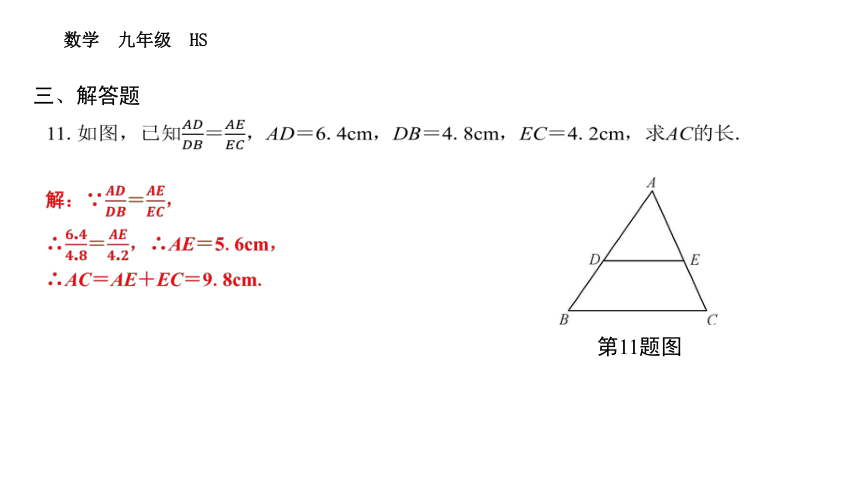
11.如图,已知=,AD=6.4cm,DB=4.8cm,EC=4.2cm,求AC的长.
第11题图
解:∵=,
∴=,∴AE=5.6cm,
∴AC=AE+EC=9.8cm.
12.如图,已知Rt△ABC中,∠ACB=90°,BC=8cm,AC=6cm,CD是斜边AB上的高,求CD∶AB的值.
第12题图
解:在Rt△ABC中,由勾股定理得:
AB==10cm,
由面积公式得:
S△ABC=AC·BC=AB·CD,
∴CD==cm,
∴CD∶AB=∶10=.
解答题
13.已知(a+b)∶(b+c)∶(c+a)=7∶14∶9,
(1)求a∶b∶c;
解:∵(a+b)∶(b+c)∶(c+a)=7∶14∶9,
∴设a+b=7k,b+c=14k,c+a=9k,
∴a=k,b=6k,c=8k,
(1)a∶b∶c=1∶6∶8;
(2)求的值.
(2)==-.
谢 谢 观 看
第2课时 平行线分线段成比例
第23章 图形的相似
一、选择题
1.如图,直线a∥b∥c,点A,B在直线a上,点C,D在直线c上,线段AC,BD分别交直线b于点E,F,则下列线段的比值与一定相等的是( B )
第1题图
A. B. C. D.
B
2.如图,已知AD∥BE∥CF,且AB=4,BC=5,EF=4,则DE=( C )
第2题图
A.5 B.3 C.3.2 D.4
C
3.如图,在△ABC中,DE∥BC,AD=5,BD=10,AE=4,则AC=( D )
第3题图
A.8 B.9 C.10 D.12
D
4.如图,在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB=( C )
第4题图
A.3∶8 B.3∶5 C.5∶8 D.2∶5
C
二、填空题
5.如图,已知AB∥CD∥EF,AF、BE相交于O,若AO=OD=DF=3cm,BE=10cm,则BO的长为 cm .
第5题图
cm
6.如图,已知a∥b∥c,AC∶CO∶OF=2∶1∶4,BE=35,那么BD= 10 .
第6题图
10
三、解答题
7.如图,已知AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若=,DE=6,求EF的长.
第7题图
解:∵AD∥BE∥CF,
∴=,
∵=,DE=6,
∴=,∴EF=9.
8.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)若AD=5,DB=6,EC=12,求AE的长;
解:(1)∵DE∥BC,
∴=,即=,
解得AE=10;
第8题图
(2)若AB=10,AD=4,AE=6,求EC的长.
解:(2)∵DE∥BC,
∴=,即=,
解得AC=15,
∴EC=AC-AE=9.
一、填空题
9.如图,在△ABC中,AB=AC,F为BC的三等分点,EF⊥BC交AB于E,若BE=2,则AB= 3 .
第9题图
3
二、解答题
10.如图,已知点O是△ABC中BC边的中点,且=,求的值.
第10题图
解:如图,过点B作BF∥AC交DE于点F,
∵BF∥AC,
∴∠FBO=∠C,∠BFO=∠CEO,
∵O为BC的中点,
∴BO=CO,
在△OBF和△OCE中,
,
∴△OBF≌△OCE(AAS),∴BF=CE,
∵=,∴=,
又∵BF∥AE,
∴==,
∴=,
∴==.
解答题
11.请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA,交BA的延长线于E,….
(1)请按照上面的证明思路,写出该证明的剩余部分;
(1)证明:如图2,过C作CE∥DA,交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,∴∠ACE=∠E,
∴AE=AC,∴=;
(2)如图3,已知在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
(2)解:∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,∴=,即=,
∴BD=BC=,
∴AD==,
∴C△ABD=AB+BD+AD=.
谢 谢 观 看
第3课时 专题黄金分割
第23章 图形的相似
一、选择题
1. 如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽、AB为长的矩形面积为S2,则S1与S2之间的大小关系为( A )
A.S1=S2
B.S1>S2
C.S1<S2
D.不能确定
第1题图
A
2.若点C是线段AB的黄金分割点,AB=8cm,AC>BC,则AC的长为( C )
A.cm B.2(-1)cm
C.4(-1)cm D.6(-1)cm
3.已知线段AB=1,C是AB的黄金分割点,AC>BC,则BC的长为( C )
A.-1 B. C. D.
4.在长度为1的线段上找到两个黄金分割点P,Q,则PQ=( D )
A. B. C.3- D.-2
C
C
D
二、填空题
5.把10米长的线段进行黄金分割,则分成的较长的线段长为 (5-5) 米.
6.点C是线段AB上的黄金分割点(AC>BC),若AC=+1,则BC的长是 2 .
(5-5)
2
三、解答题
7.若线段AB=4cm,点C是线段AB的黄金分割点,AC>BC,求AC-BC的值.
解:∵点C是线段AB的黄金分割点,AC>BC,
∴AC=AB=(2-2)cm,
∴BC=AB-AC=(6-2)cm,
∴AC-BC=(4-8)cm.
8.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长xcm与身高lcm的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为多少?(精确到1cm)
第8题图
解:由题意得x=165×0.60=99,
设需要穿的高跟鞋的高度是ycm,
则根据黄金分割的定义,
得=0.618,解得y≈8,
答:她应穿的高跟鞋的高度大约为8cm.
9.如图,△ABC是顶角为36°的等腰三角形,已知底与腰的比为的三角形是黄金三角形,若△ABC、△BDC、△DEC都是黄金三角形,且AB=4,求DE的长.
第9题图
解:∵△ABC是黄金三角形,
∴BC=AB=2-2,
∵△BCD是黄金三角形,
∴CD=BC=6-2,
∵△DEC是黄金三角形,
∴DE=CD=6-2,
即DE的长为6-2.
一、填空题
10.著名数学家华罗庚(1910-1985)倡导优选法,就是对生产和科学试验中提出的问题,根据数学原理,通过尽可能少的试验次数,迅速求得最佳方案的方法.这个数学原理就是利用中国古代黄金分割比值的近似值0.618乘以任意一个数,所得的另一个数,就是最佳的方案.某医院急诊室的护士利用体温表给病人量体温,按常规测一次体温需3分钟时间,实际上是 1.854 分钟时测的体温,同3分钟时测的体温一样,这 1.854 分钟与 1.146 分钟之间的分界点,就是用优选法产生出来的.
1.854
1.854
1.146
二、解答题
11.如果一个矩形的宽与长的比值为,那么称这个矩形为黄金矩形.如图,将矩形ABCD剪掉一个正方形ADFE后,剩余的矩形BCFE(BC>BE)是黄金矩形,则原矩形ABCD是否为黄金矩形?请说明理由.
第11题图
解: 原矩形ABCD是黄金矩形,
理由: 设矩形BCFE的长BC=x,
∵矩形BCFE为黄金矩形,
∴宽BE=x,
∵四边形AEFD是正方形,
∴AE=EF=BC=x,
∴AB=x+x=x,
∴==,
∴原矩形ABCD是黄金矩形.
解答题
12.如图,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(1)解:在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF-PA=PD-PA=-1,
DM=AD-AM=2-(-1)=3-;
第12题图
(2)求证:AM2=AD·DM;
(2)证明:∵AM2=(-1)2=6-2,AD·DM=2(3-)=6-2,
∴AM2=AD·DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
(3)解:∵AM2=AD·DM,==,
∴点M是AD的黄金分割点.
谢 谢 观 看
第4课时 相似图形
第23章 图形的相似
一、选择题
1.下列说法正确的是( C )
A.菱形都是相似图形
B.各边对应成比例的多边形是相似多边形
C.等边三角形都是相似三角形
D.矩形都是相似图形
C
2.若五边形ABCDE∽五边形A1B1C1D1E1,且=3,则五边形A1B1C1D1E1与五边形ABCDE的相似比是( B )
A.3∶1 B.1∶3
C.1∶9 D.无法确定
3.已知矩形ABCD中,AB=4,BC=3,下列矩形与矩形ABCD相似的是( A )
A. B.
C. D.
B
A
二、填空题
4.一个四边形的各边长之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为 20 cm.
5. ABCD和 EFGH中,AB=3,BC=5,∠B=40°,EF=6,要使 ABCD∽ EFGH,则FG= 10 ,∠F= 40° .
6.如图,已知四边形ABCD与四边形A'B'C'D'相似,则∠B'= 60° .
20
10
40°
60°
第6题图
三、解答题
7.如图,等腰梯形ABCD与等腰梯形A'B'C'D'相似,∠A'=65°,A'B'=6cm,AB=8cm,AD=5cm,试求梯形ABCD的各角的度数与A'D',B'C'的长.
第7题图
解:∵等腰梯形ABCD与等腰梯形A'B'C'D'相似,∠A'=65°,
∴∠A=∠A'=65°,∠B=∠A=65°,∠D=∠C=180°-65°=115°,
∵等腰梯形ABCD与等腰梯形A'B'C'D'相似,
∴=,即=,
∴A'D'=cm,
∴B'C'=A'D'=cm.
8.如图,有一块长为2m、宽为1m的矩形玻璃ABCD,为了保护玻璃,需要镶上宽10cm的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?
第8题图
解:不相似,理由如下:
∵AB=2m,AD=1m,
∴EF=2-0.1×2=1.8m,
∴EN=1-0.1×2=0.8m,
∴==0.9,==0.8,
∵≠,
∴边框的内外边缘所成的矩形不相似.
一、填空题
9.下列说法正确的有 ②④ .(填序号)
①在两个边数相同的多边形中,如果各对应边成比例,那么这两个多边形相似;②两个矩形有一组邻边对应成比例,这两个矩形相似;③有一个角对应相等的平行四边形都相似;④有一个角对应相等的菱形都相似.
10.将一张报纸对折后,若对折后的半张报纸和整张报纸相似,则整张报纸的长和宽的比是 ∶1 .
②④
∶1
二、解答题
11.如图,矩形花坛ABCD的宽AB=20米,长AD=30米.现计划在该花坛四周修筑小路,使小路四周所围成的矩形A'B'C'D'与矩形ABCD相似,并且相对的两条小路的宽相等,试问小路的两个宽x与y的比值是多少?
第11题图
解:根据题意得A'B'=AB+2y,A'D'=AD+2x,
∵矩形A'B'C'D'∽矩形ABCD,
∴A'B'∶A'D'=AB∶AD,
∴(20+2y)∶(30+2x)=20∶30,
∴=,
即小路的两个宽x与y的比值是.
解答题
12.已知矩形ABCD中,AD=3,AB=1.
(1)若EF把矩形分成两个小的矩形,如图所示,其中矩形ABEF与矩形ABCD相似,求AF∶AD;
解:(1)设AF=x,
∵矩形ABEF与矩形ABCD相似,AD=3,AB=1,
∴=,即=,解得x=,
∴AF∶AD=∶3=1∶9;
第12题图
(2)若在矩形ABCD内不重叠地放两个长是宽的3倍的小矩形,且每个小矩形的每条边与矩形ABCD的边平行,求这两个小矩形的周长和的最大值.
解:(2)两个小矩形的放置情况有如下几种:
①如图1,两个小矩形都“竖放”,
在这种放法下,周长和最大的两个小矩形,两边长分别为1和 ,
此时两个小矩形的周长和的最大值为 ;
第12题图
图1
图1
②如图2、图3,两个小矩形都“横放”,
此时两个小矩形的周长和的最大值为:
2(a+3a)+2[1-a+3(1-a)]=8;
图2
图3
图2
图3
③如图4,两个小矩形一个“横放”,一个“竖放”,
此时两个小矩形的周长和为:
2(a+3a)+2(3-a+)=8+,
∵0<3a≤1,即0<a≤,
∴当a=时,两个小矩形的周长和最大,为 ,
综上所述,这两个小矩形的周长和的最大值为.
图4
图4
谢 谢 观 看
第5课时 相似三角形
第23章 图形的相似
一、选择题
1.(1)已知△ABC∽△DEF,AB∶DE=3∶1,AB=6,则DE的长为( B )
A.18 B.2 C.54 D.
(2)已知△ADE∽△ABC,且相似比为,若DE=8,则BC的长是( D )
A. B.6 C.8 D.12
B
D
2.如图,在△ABC中,DE∥BC,AD=3BD,DE=3,则BC的长为( C )
第2题图
A.1 B. C.4 D.6
C
3.如图,AB∥CD,若AB=12,CD=4,AO=9,则CO的长是( B )
第3题图
A. B.3 C.4.5 D.6
B
二、填空题
4.若△ABC∽△A'B'C',∠A=50°,∠C=110°,则∠B'的度数为 20° .
5.如图,在△ABC中,AB=4,AC=3,D是AB边上的一点,若△ABC∽△ACD,则AD的长为 .
第5题图
20°
6.如图,AB∥CD,AC,BD,EF相交于点O,则图中相似的三角形共有 3 对.
第6题图
3
三、解答题
7.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
第7题图
解:∵△ADE∽△ABC,
∴==,
∵DE=4,BC=12,CD=9,AD=3,
∴AC=AD+CD=12,
∴==,
∴AE=4,AB=9,
∴BE=AB-AE=5.
8.如图,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:
(1)∠AED和∠ADE的度数;
解:(1)∵DE∥BC,∠C=40°,
∴∠AED=∠C=40°,
∵∠A=45°,
∴∠ADE=180°-∠A-∠AED=95°;
第8题图
(2)DE的长.
解:(2)∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵AE=50cm,EC=30cm,BC=70cm,
∴=,
∴DE=cm.
一、填空题
9.如图,在矩形ABCD中,作DF⊥AC,垂足为F,延长DF交边AB于点E,在图中一定和△DFC相似的三角形有 5 个.
第9题图
5
10.如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则的值是 .
第10题图
二、解答题
11.如图,在 ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,求AC的长.
第11题图
解:如图,延长FE交CB的延长线于点H,
∵四边形ABCD是平行四边形,
∴BC=AD=AF+DF=6cm,BC∥AD,
∴∠EAF=∠EBH,∠AFE=∠BHE,
∵E为AB的中点,∴AE=BE,
∴△AFE≌△BHE(AAS),
∴BH=AF=2cm,∴CH=BH+BC=8cm,
∵BC∥AD,
∴AG∶CG=AF∶CH,
即3∶CG=2∶8,∴CG=12cm,
∴AC=AG+CG=15cm.
解答题
12.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
①当=时,=;
②当=时,=;
③当=时,=;
….
猜想当=时,的值,并说明理由.
第12题图
解:猜想:当=时,=,理由如下:
如图,过点D作DG∥BE,交AC于点G,
则==,
∴=,∴EG=nAE,
∵AD是△ABC的中线,且DG∥BE,
∴EG=CG,∴AC=(2n+1)AE,
∴=.
谢 谢 观 看
第6课时 相似三角形的判定(1)
第23章 图形的相似
一、选择题
1.下列条件中,一定能判断两个等腰三角形相似的是( C )
A.都含有一个40°的内角
B.都含有一个50°的内角
C.都含有一个60°的内角
D.都含有一个70°的内角
C
2.如图,在△ABC中,D,E分别为AC、BC边上的点,若∠1=∠2=∠3,则图中相似的三角形共有( D )
第2题图
A.1对 B.2对 C.3对 D.4对
D
3.如图,在△ABC中,D、E分别为AB、AC边上的点,且∠AED=∠B,AD=3,AC=6,DB=5,则AE的长度为( D )
第3题图
A. B. C. D.4
D
二、填空题
4.如图,要使△ABC∽△ACD,需补充的条件是 ∠ACD=∠B(或∠ADC=∠ACB) .(写出一种即可)
第4题图
∠ACD=∠B(或∠ADC=
∠ACB)
5.如图,D为△ABC的AB边上的一点,∠DCA=∠B,若AC=cm,AB=3cm,则AD的长为 2cm .
第5题图
2cm
三、解答题
6.如图,点D,E在BC上,且FD∥AB,FE∥AC,求证:△ABC∽△FDE.
第6题图
证明:∵FD∥AB,FE∥AC,
∴∠B=∠FDE,∠C=∠FED,
∴△ABC∽△FDE.
7.如图,已知△PQR是等边三角形,∠APB=120°,求证:△PAQ∽△BPR.
第7题图
证明:∵△PQR是等边三角形,
∴∠PQR=∠PRQ=60°,
∴∠PQA=∠BRP=120°,
∵∠PQR是△PQA的外角,
∴∠PQR=∠APQ+∠PAQ=60°,
∵∠APB=120°,
∴∠PAQ+∠PBR=60°,
∴∠APQ=∠PBR,
∴△PAQ∽△BPR.
8.如图,在 ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
第8题图
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠C+∠D=180°,∠BAF=∠AED,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
一、填空题
9.如图,直线y=-2x+4与x轴,y轴分别相交于A,B两点,C为OB上一点,若∠1=∠2,则S△ABC= 3 .
第9题图
3
10.如图,在 ABCD中,AD=10cm,CD=6cm,E为AD上一点,若BE=BC,CE=CD,则DE= 3.6 cm.
第10题图
3.6
二、解答题
11.如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.
(1)求证:△COM∽△CBA;
(1)证明:∵A与C关于直线MN对称,
∴AC⊥MN,∠COM=90°,
在矩形ABCD中,∠B=90°,
∴∠COM=∠B,
又∵∠MCO=∠ACB,
∴△COM∽△CBA;
第11题图
(2)求线段OM的长.
(2)解:∵在Rt△CBA中,AB=6,BC=8,
∴AC==10,∴OC=5,
∵△COM∽△CBA,
∴=,即=,
∴OM=.
解答题
12.如图,已知正方形DEFG内接于Rt△ABC,EF在斜边BC上,EH⊥AB于H,求证:
(1)△ADG≌△HED;
证明:(1)如图,
∵四边形DEFG为正方形,
∴∠EDG=90°,DG=ED,
∴∠1+∠2=90°,
∵EH⊥AB,
∴∠2+∠3=90°,
∴∠1=∠3,
∵∠A=∠EHD=90°,DG=ED,
∴△ADG≌△HED(AAS);
第12题图
(2)EF2=BE·FC.
证明:(2)∵四边形DEFG为正方形,
∴∠DEF=∠EFG=90°,DE=GF=EF,
∴∠DEB=∠CFG=90°,
在Rt△ABC中,∠B+∠C=90°,
在Rt△BDE中,∠B+∠2=90°,
∴∠2=∠C,
∴△BDE∽△GCF,
∴=,
∵DE=GF=EF,
∴=,
∴EF2=BE·FC.
谢 谢 观 看
第7课时 相似三角形的判定(2)
第23章 图形的相似
一、选择题
1.下列条件中,不能判定△ABC和△DEF相似的是( D )
A.∠A=∠D=70°,∠B=60°,∠E=50°
B.∠A=∠D=70°,∠C=50°,∠E=50°
C.∠A=∠D=70°,AB=12cm,AC=15cm,ED=16cm,DF=20cm
D.∠A=∠D=70°,AB=12cm,AC=15cm,ED=16cm,EF=20cm
D
2.如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( D )
第2题图
A.AB∥CD B.∠A=∠D
C.= D.=
D
二、填空题
3.如图,若= ,则△OAC∽△OBD.
第3题图
4.如图,△ABC中,D为AB上一点,若AC2=AD·AB,则△ABC∽ △ACD .
第4题图
△ACD
5.如图,在四边形ABCD中,已知∠A=∠CBD,AB=15cm,AD=20cm,BD=18cm,BC=24cm,则CD的长为 cm.
第5题图
三、解答题
6.如图,已知∠BAE=∠CAD,AB=18,AC=48,AE=15,AD=40,求证:△ABC∽△AED.
第6题图
证明:∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,
即∠BAC=∠EAD,
∵AB=18,AC=48,AE=15,AD=40,
∴==,
∴△ABC∽△AED.
7.如图,在△ABC中,BD⊥AC于点D,DE⊥AB于点E,BD·DE=BE·CD,求证:△BCD∽△BDE.
第7题图
证明:∵BD⊥AC,DE⊥AB,
∴∠BDC=∠BED=90°,
∵BD·DE=BE·CD,
∴=,
∴△BCD∽△BDE.
8.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,△ABC和△DEF的顶点都在边长为1的小正方形的格点上.
(1)∠ABC= °,BC= ;
解:(1)135,2;
第8题图
(2)判断△ABC与△DEF是否相似,若相似,请说明理由.
解:(2)△ABC∽△DEF.理由如下:
∵AB=2,BC=2,DE=,EF=2,
∴==,
又∵∠ABC=∠DEF=135°,
∴△ABC∽△DEF.
一、填空题
9.如图,∠A=∠B=90°,AB=7,BC=3,AD=2,在边AB上取点P,使得△PAD与△PBC相似,则满足条件的AP长为 2.8或1或6 .
第9题图
2.8或1或6
二、解答题
10.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CF=3FD.
(1)求证:△ABE∽△DEF;
(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴==2,==2,
∴=,
又∵∠A=∠D=90°,
∴△ABE∽△DEF;
第10题图
(2)△ABE与△EBF相似吗?为什么?
(2)解:△ABE∽△EBF,理由如下:
∵△ABE∽△DEF,
∴==,∠ABE=∠DEF,
∵∠AEB+∠ABE=90°,
∴∠AEB+∠DEF=90°,∴∠BEF=90°,
又∵=,∠A=90°,
∴==,∠A=∠BEF=90°,
∴△ABE∽△EBF.
解答题
11.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,P、Q两点同时出发,设移动时间为ts.
(1)当t为何值时,△PBQ是等腰三角形?
(1)∵△PBQ是等腰三角形,∠B=90°,
∴BP=BQ,即6-t=2t,解得t=2,
∴当t=2时,△PBQ是等腰三角形;
第11题图
解:由题意得BP=(6-t)cm,BQ=2tcm,
(2)当t为何值时,△PBQ的面积为5cm2?
(2)S△PBQ=BP·BQ=(6-t)·2t=5,
即(t-1)(t-5)=0,解得t=1或5,
∴当t=1或5时,△PBQ的面积为5cm2;
(3)当t为何值时,△PBQ和△ABC相似?
(3)①若△BPQ∽△BAC,则=,
即=,解得t=3;
②若△BPQ∽△BCA,则=,
即=,解得t=1.2,
综上所述,当t=3或1.2时,△PBQ和△ABC相似.
谢 谢 观 看
第8课时 相似三角形的判定(3)
第23章 图形的相似
一、选择题
1.甲三角形的三边长分别为9,6,12,乙三角形的三边长分别为4,6,8,则这两个三角形( C )
A.一定不相似 B.不一定相似
C.一定相似 D.无法判断是否相似
C
2.在下列条件中,不能判断△ABC与△DEF相似的是( B )
A.==
B.=且∠B=∠E
C.=且∠A=∠D
D.∠A=∠D,∠B=∠E
B
3.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与如图所示的△ABC相似的三角形所在的网格图形是( B )
第3题图
A
B
C
D
B
二、填空题
4.已知在△ABC中,AB=4,BC=5,CA=6.
(1)如果DE=10,那么当EF= 12.5 ,FD= 15 时,△DEF∽△ABC;
(2)如果DE=10,那么当EF= 12 ,FD= 8 时,△FDE∽△ABC.
5.在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,则当= 2 时,△ABC∽△DEF.
12.5
15
12
8
2
三、解答题
6.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
(1)AB=12,BC=15,AC=24,A'B'=25,B'C'=40,C'A'=20;
解:(1)△ABC∽△C'A'B',理由如下:
∵==,==,==,
∴==,
∴△ABC∽△C'A'B';
(2)AB=3,BC=4,AC=5,A'B'=12,B'C'=16,C'A'=20.
解:(2)△ABC∽△A'B'C',理由如下:
∵==,==,==,
∴==,
∴△ABC∽△A'B'C'.
7.如图,在由边长为1的小正方形组成的网格中有A、B、C、D、E五个点,问△ABC与△ADE是否相似?为什么?
第7题图
解:△ABC∽△ADE,理由如下:
由图可知,AB==2,BC=10,
AC==2,AE=2,AD=,
DE==,
∴===,
∴△ABC∽△ADE.
一、填空题
8.如图,在Rt△ABC和Rt△ACD中,∠ACB=∠ADC=90°,AC=,AD=2,则当AB= 3或3 时,△ABC与△ACD相似.
第8题图
3或3
9.如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为 3 .
第9题图
3
二、解答题
10.如图,点B、D、E在同一条直线上,BE与AC相交于点F,==.
(1)求证:∠BAD=∠CAE;
(1)证明:∵==,
∴△ABC∽△ADE,∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,
∴∠BAD=∠CAE;
第10题图
(2)若∠BAD=21°,求∠EBC的度数;
(2)解:∵△ABC∽△ADE,
∴∠ABC=∠ADE,
∵∠ABC=∠ABE+∠EBC,
∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=21°;
(3)连接EC,求证:△ABD∽△ACE.
(3)证明:由(1)知∠BAD=∠CAE,
又∵=,即=,
∴△ABD∽△ACE.
解答题
11.如图,在平面直角坐标系中,梯形OABC的边OA在x轴上,OC在y轴上,OA∥BC,点E在对角线OB上,点D在OC上,直线DE与x轴交于点F,已知OE=2EB,CB=3,OA=6,BA=3,OD=5.
第11题图
(1)证明:如图,过点B作BG⊥OA于点G,
∴四边形OCBG是矩形,
∴BG=OC,OG=BC=3,AG=OA-OG=3,
由勾股定理,得BG==6,
∴OC=BG=6,
由勾股定理,得OB==3,
∵OE=2EB,∴OE=OB=2,
∵==,且∠DOE=∠BOC,
∴△ODE∽△OBC;
(1)求证:△ODE∽△OBC;
(2)在y轴上找一点P,使得△PFO∽△ODE,直接写出点P的坐标.
(2)解:∵△ODE∽△OBC,
∴∠OED=∠OCB=90°,
∴∠OED=∠FOD=90°,DE==,
又∵∠ODE=∠FDO,∴△DOE∽△DFO,
∴=,即=,∴FO=10,
∵△PFO∽△ODE,
∴=,即=,∴PO=20,
∴点P的坐标为(0,20)或(0,-20).
谢 谢 观 看
第9课时 专题相似三角形的判定
第23章 图形的相似
解答题
1. 如图,在△ABC中,∠C=90°,DE⊥AB于点E,DF⊥BC于点F,DF交AB于点H,求证:△DEH∽△BCA.
第1题图
证明:∵DE⊥AB,DF⊥BC,
∴∠D+∠DHE=∠B+∠BHF=90°,
∵∠BHF=∠DHE,
∴∠D=∠B,
又∵∠DEH=∠C=90°,
∴△DEH∽△BCA.
2.如图,点D在△ABC的边AB上,AD=1,BD=2,AC=,求证:△ACD∽△ABC.
第2题图
证明:∵==,=,
∴=,
∵∠A=∠A,
∴△ACD∽△ABC.
3.如图,△ABC中,D、E分别在边AB、AC上,AD=2BD,AE=2CE,=,求证:△ABC与△ADE相似.
第3题图
证明:∵AD=2BD,AE=2CE,
∴=,=,
∵=,
∴==,
∴△ADE∽△ABC.
4.如图,在矩形ABCD中,BC=12cm,AB=8cm,P、Q分别是AB、BC上的两动点.若点P自点A出发,以1cm/s的速度沿AB方向运动,同时,点Q自点B出发,以2cm/s的速度沿BC方向运动,问经过几秒,△PBQ与△BCD相似?
第4题图
解:如图,
设经过xs,△PBQ与△BCD相似,
则AP=xcm,PB=(8-x)cm,BQ=2xcm,
由于∠PBQ=∠BCD=90°,
①当∠1=∠2时,△PBQ∽△DCB,
∴=,即=,
解得x=;
②当∠1=∠3时,△PBQ∽△BCD,
∴=,即=,
解得x=2,
∴经过s或2s,△PBQ与△BCD相似.
解答题
5.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(1)证明:由勾股定理得:AB2=22+42=20,AC2=22+12=5,BC2=32+42=25,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
第5题图
(2)判断△ABC和△DEF是否相似,并说明理由;
(2)解:△ABC与△DEF相似,
理由:由勾股定理得:DF==2,DE==4,EF==2,
由(1)知:AB=2,AC=,BC=5,
∴===,
∴△ABC∽△DEF;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
(3)解:如图,和△ABC相似的三角形是△P4P5P2,
理由:由勾股定理得:P5P2==,P4P2==,P4P5==2,
∵AB=2,AC=,BC=5,
∴===,
∴△ABC∽△P4P5P2.
解答题
6.如图,在平面直角坐标系xOy内,点A(6,0)、C(-4,0),过点A作直线AB,交y轴的正半轴于点B,且AB=10,点P是直线AB上的一个动点.
(1)求点B的坐标和直线AB的表达式;
解:(1)∵A(6,0),∴OA=6,
∴OB==8,
∵点B在y轴的正半轴,
∴点B的坐标为(0,8),
设直线AB的表达式为y=kx+b(k≠0),
将A(6,0),B(0,8)代入y=kx+b,
得,解得,
∴直线AB的表达式为y=-x+8;
第6题图
(2)若△APC与△AOB相似,求点P的坐标.
解:(2)如图,分两种情况考虑,
①当△AOB∽△ACP1时,∠ACP1=∠AOB=90°,
∵当x=-4时,y=-x+8=,
∴点P1的坐标为(-4,);
②当△AOB∽△AP2C时,设P2(m,-m+8),
∵A(6,0),C(-4,0),∴AC=10,
∵△AOB∽△AP2C,∴=,即=,
解得CP2=8,
∴=8,
整理,得:(m-4)2=0,解得m=,
∴点P2的坐标为(,),
综上所述,点P的坐标为(-4,)或(,).
谢 谢 观 看
第10课时 相似三角形的性质
第23章 图形的相似
一、选择题
1.若两个相似三角形的相似比是2∶5,则对应高的比是( A )
A.2∶5 B.4∶25 C. D.25∶4
2.已知两个相似三角形的相似比是2∶3,其中较小三角形的一条中线长6cm,则较大三角形中对应的中线长为( D )
A.4cm B.6cm C.8cm D.9cm
3.若两个相似三角形的面积之比为1∶9,则它们的周长之比为( A )
A.1∶3 B.3∶1 C.1∶9 D.9∶1
A
D
A
二、填空题
4.两个相似三角形对应边上中线的比为3∶2,则对应边上的高的比为 3∶2 ,周长之比为 3∶2 ,面积之比为 9∶4 .
5.如果两个相似三角形对应角平分线的比是2∶3,它们一条对应高的差为5cm,那么这两条对应高的长分别是 10cm,15cm .
6.已知两个相似三角形的相似比为2∶5,其中较小的三角形面积是4,那么另一个三角形的面积为 25 .
3∶2
3∶2
9∶4
10cm,15cm
25
三、解答题
7.已知△ABC∽△A'B'C',=,AB边上的中线CD=4cm,△ABC的周长为20cm,△A'B'C'的面积是64cm2,求:
(1)A'B'边上的中线C'D'的长;
解:(1)∵△ABC∽△A'B'C',=,
∴=,
∴C'D'=4×2=8cm,
∴A'B'边上的中线C'D'的长为8cm;
(2)△A'B'C'的周长;
解:(2)∵△ABC∽△A'B'C',=,
∴=,
∴C△A'B'C'=20×2=40cm,
∴△A'B'C'的周长为40cm;
(3)△ABC的面积.
解:(3)∵△ABC∽△A'B'C',=,
∴==,
∴S△ABC=64÷4=16cm2,
∴△ABC的面积是16cm2.
8.如图,在△ABC中,BC=120mm,点Q,M在BC上,点P,N分别在AB,AC上,四边形PQMN为矩形,△ABC的高AD与PN相交于点E,且AD=80mm.
(1)若这个矩形是正方形,则边长是多少?
解:(1)设正方形PQMN的边长为xmm,
∵四边形PQMN为正方形,
∴PN∥QM,∴△APN∽△ABC,
∴=,即=,
解得x=48,
∴正方形PQMN的边长是48mm;
第8题图
(2)若这个矩形的长是宽的2倍,则长和宽各是多少?
解:(2)设矩形PQMN的宽为ymm,
由(1)得△APN∽△ABC,
∴=,即=,或=,
解得y=30或,
∴矩形PQMN的宽为30mm,长为60mm或宽为mm,长为mm.
一、填空题
9.如图,在 ABCD中,E为CD上一点,DE∶CE=2∶3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF∶S△EBF∶S△ABF= 4∶10∶25 .
第9题图
4∶10∶25
10.如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,…,如此作下去,则所作的第n个正方形的面积Sn= .
第10题图
二、解答题
11.如图,四边形ABCD中,AD∥BC,∠ACD=∠B,求证:=.
第11题图
证明:∵AD∥BC,∴∠ACB=∠DAC,
∵∠ACD=∠B,∴△ACB∽△DAC,
∴=()2,
又∵AD∥BC,∴=,
∴()2=,即=.
解答题
12.如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A,C不重合)在AC边上,EF∥AB交BC于点F.试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若存在,请求出EF的长;若不存在,请简要说明理由.
第12题图
解:存在.
∵EF∥AB,∴△ECF∽△ACB,
△EFP为等腰直角三角形,有三种情况:
①如图1,过点C作CD⊥AB于点D,
当∠PEF=90°,EP=EF时,
由AB=5,BC=3,AC=4,得∠ACB=90°,
∴Rt△ACB斜边AB上的高CD=,
设EP=EF=x,
由△ECF∽△ACB,得:=,
即=,解得x=,即EF=;
图1
②如图1,当∠EFP'=90°,EF=FP'时,
同①理可得EF=;
图1
③如图2,当∠EP″F=90°,P″E=P″F时,
过点P″作P″H⊥EF于点H,过点C作CD⊥AB于点D,
∴P″H=EF,
设EF=x,则P″H=x,
由△ECF∽△ACB,得:=,
即=,解得x=,即EF=,
综上所述,在AB上存在点P,使得△EFP为等腰直角三角形,此时EF=或.
图2
谢 谢 观 看
第11课时 专题比例线段的证明
第23章 图形的相似
解答题
1.如图,在△ABC与△DBE中,∠A=∠D,∠ABD=∠CBE.求证:BD·BC=BA·BE.
第1题图
证明:∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,
∵∠A=∠D,∴△ABC∽△DBE,
∴=,∴BD·BC=BA·BE.
2.如图,在 ABCD中,M,N分别是AD,BC上的点,ME⊥BD,NF⊥BD,垂足分别是E,F,求证:=.
第2题图
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠MDE=∠NBF,
∵ME⊥BD,NF⊥BD,
∴∠MED=∠NFB=90°,
∴△MED∽△NFB,∴=.
3.如图,在Rt△ABC中,∠C=90°,点E,F在AB上,点D,G分别在BC,AC上,且四边形DEFG是正方形,求证:EF2=BE·AF.
第3题图
证明:∵∠C=90°,
∴∠A+∠B=90°,
∵四边形DEFG是正方形,
∴∠AFG=∠DEB=90°,GF=EF=DE,
∴∠A+∠AGF=90°,∴∠AGF=∠B,
∴△AFG∽△DEB,∴=,即=,
∴EF2=BE·AF.
4.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,求证:AE·AB=AF·AC.
第4题图
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵DE⊥AB,
∴∠AED=∠ADB=90°,
又∵∠BAD=∠DAE,
∴△ABD∽△ADE,
∴=,∴AD2=AE·AB,
同理:AD2=AF·AC,
∴AE·AB=AF·AC.
5.如图,在△ABC中,AM是BC边上的中线,直线DN∥AM,交AB于点D,交CA的延长线于点E,交BC于点N.求证:=.
第5题图
证明:∵直线DN∥AM,∴=,=,
∵在△ABC中,AM是BC边上的中线,
∴MB=MC,∴=.
6.如图,已知△ABC中,D为AC上一点,E为CB延长线上一点,BE=AD,ED和AB相交于点F,求证:EF∶FD=AC∶BC.
第6题图
证明:如图,过点D作DG∥BC,交AB于点G,
则△ADG∽△ACB,△DGF∽△EBF,
∴=,=,∴=,
∵BE=AD,∴==,
即EF∶FD=AC∶BC.
解答题
7.在四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,∴∠ADE+∠DFC=90°,
∴∠AED=∠DFC,∴△ADE≌△DCF(AAS),∴DE=CF;
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:=;
(2)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,∴∠DCF+∠CFD=90°,
∵DE⊥CF,∴∠ADE+∠CFD=90°,∴∠ADE=∠DCF,
∴△ADE∽△DCF,∴=;
(3)如图3,若四边形ABCD是平行四边形,试探究:当∠B与∠EGF满足什么关系时,=成立?并证明你的结论.
(3)解:当∠B=∠EGF时,=成立,
证明:如图,在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM,
∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠A=∠CDM,∠B+∠A=180°,
∵∠B=∠EGF,∴∠EGF+∠A=180°,
∴∠AED=∠CFM=∠CMF,∴△ADE∽△DCM,
∴=,即=.
解答题
8.如图1,△ABC中,∠ACB=90°,射线CD⊥AB于点D.点P是射线CD上一动点,连接AP并在AP边右侧作△APQ,使得∠PAQ=∠CAB且=,连接BQ.
(1)求证:BA平分∠CBQ;
(1)证明:∵CD⊥AB,∠ACB=90°,
∴∠CAB+∠ABC=∠CAB+∠ACD=90°,
∴∠ACD=∠ABC,
∵∠PAQ=∠CAB,=,
∴∠PAC=∠QAB,=,
∴△CAP∽△BAQ,∴∠ACP=∠ABQ,
∴∠ABC=∠ABQ,∴BA平分∠CBQ;
(2)当AQ∥BC时,如图2,延长AP交BC边于点E,求证:CE·BC=AD·AB;
(2)证明:∵AQ∥BC,∴∠QAB=∠CBA,
由(1)得∠CAE=∠QAB,∴∠CAE=∠CBA,
又∵∠ACE=∠BCA=90°,∴△ACE∽△BCA,
∴=,∴AC2=CE·BC,
∵∠CAD=∠BAC,∠ACD=∠ABC,
∴△ACD∽△ABC,∴=,∴AC2=AD·AB,
∴CE·BC=AD·AB;
(3)若AC=3,BC=4,点P在运动的过程中,直线PQ交边AB于点F,当△BQF是等腰三角形时,求线段AP的长.
(3)解:如图,设射线BQ交CD于点W,连接AW,
①如图1,当BF=BQ时,
∵∠ABC=∠ABW,∴点C,W关于AB对称,
∴AC=AW=3,∠AWB=∠ACB=90°,
∵∠PAQ=∠CAB,=,
∴△ACB∽△APQ,∴∠APQ=∠ACB=90°,
∴∠APQ+∠AWQ=180°,∴∠BQF=∠WAP,
∵BF=BQ,∴∠BQF=∠BFQ=∠AFP,
∵∠APD+∠DPF=∠DPF+∠PFD=90°,
∴∠APD=∠AFP,∴∠WAP=∠APW,∴AW=PW=3,
在Rt△ABC中,∵AC=3,BC=4,∴AB=5,
∵AC2=AD·AB,∴AD=,∴DW==,
∴DP=PW-DW=,∴AP==;
②如图2,当FQ=FB时,易证AP=PW,
∴DP=DW-PW=-AP,
在Rt△ADP中,AD2+DP2=AP2,
即()2+(-AP)2=AP2,
解得AP=;
③∵∠BFQ>∠AQP=∠ABQ,∴FQ≠BQ,
综上所述,满足条件的AP的长为或.
谢 谢 观 看
第12课时 相似三角形的应用
第23章 图形的相似
一、选择题
1.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是18m,则旗杆的高度是( C )
A.9m B.11m C.12m D.27m
C
2.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C到旗杆底部D的距离是4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A到小丽头顶的距离是4cm,则旗杆DE的高度为( B )
B
第2题图
A.10m B.12m C.12.4m D.12.32m
二、填空题
3.如图,小明在打网球时,网高0.9m,击球点到球网的水平距离是10m,要使球恰好能打过网,而且落在离网5m的位置上,则球拍击球的高度h应为 2.7 m.
第3题图
2.7
4.如图是斜靠在墙壁上的长梯,梯脚B距离墙1.6m,梯上点D距离墙1.4m,BD的长为0.55m,则梯子的长为 4.4m .
第4题图
4.4m
三、解答题
5.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的这一侧选点A,B,D,使AB⊥AO,DB⊥AB,然后确定DO和AB的交点C,测得AC=120m,CB=60m,BD=50m,请你帮助他们算出峡谷的宽AO.
第5题图
解:∵AB⊥AO,DB⊥AB,∴∠A=∠B=90°,
∵∠ACO=∠BCD,
∴△ACO∽△BCD,
∴=,
∵AC=120m,CB=60m,BD=50m,
∴=,∴AO=100m,
答:峡谷的宽AO是100m.
6.如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.请你利用小明测量的数据算出电线杆AB的高.
第6题图
解:如图,过点C作CG⊥AB于点G,
∴GC=BD=3米,GB=CD=2米,
∵太阳光线是平行光线,
∴∠NFM=∠ACG,
∵∠NMF=∠AGC=90°,
∴△NMF∽△AGC,
∴=,
∴AG==6米,
∴AB=AG+GB=8米,
答:电线杆AB的高为8米.
一、选择题
7.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( B )
第7题图
B
A.4 m B.m C.5m D.m
二、填空题
8.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为15cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座点B,若不考虑其它因素,此时该台灯在桌面可照亮的宽度BD的长为 75 cm.
第8题图
75
三、解答题
9.如图,某同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时尺子的刻度为12cm,已知臂长60cm,求电线杆的高度.
第9题图
解:如图,∵DF∥EC,
∴△ADF∽△AEC,
∴=,
∵GF⊥EC,BC⊥EC,
∴GF∥BC,
∴△AGF∽△ABC,∴=,∴=,
∵DF=0.6m,GF=0.12m,EC=30m,
∴=,∴BC=6m,
答:电线杆的高度为6m.
解答题
10.如图,学校的围墙外有一旗杆AB,甲在操场上C处直立3m高的竹竿CD,乙从C处退到E处恰好看到竹竿顶端D,与旗杆顶端B重合,量得CE=3m,乙的眼睛到地面的距离FE=1.5m,丙在C1处也直立3m高的竹竿C1D1,乙从E处退后6m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旗杆顶端B也重合,测得C1E1=4m,求旗杆AB的高.
第10题图
解:设BO=xm,GO=ym,
∵GD∥OB,
∴△DGF∽△BOF,
∴=,
即=①,
同理可得:△D1HF1∽ △BOF1,
∴=,
即=②,
联立①、②解得,
∴旗杆AB的高为9+1.5=10.5m.
谢 谢 观 看
第13课时 三角形的中位线
第23章 图形的相似
一、选择题
1.已知三角形的周长是16,则它的三条中位线围成的三角形的周长是( C )
A.16 B.12 C.8 D.4
2.如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,已知∠ADE=65°,则∠CFE的度数为( B )
A.60°
B.65°
C.70°
D.75°
第2题图
C
B
二、填空题
3.如图,在△ABC中,AE是BC边上的中线,点G是△ABC的重心,过点G作GF∥AB交BC于点F,那么= .
第3题图
4.如图, ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 3 厘米.
第4题图
3
三、解答题
5.如图,△ABC中,D,E,F分别是AB,AC,BC的中点.
(1)若EF=5cm,则AB= cm,
若BC=9cm,则DE= cm;
解:(1)∵D,E,F分别是AB,AC,BC的中点,
∴AB=2EF=10cm,DE=BC=4.5cm,
故答案为:10,4.5;
第5题图
(2)中线AF与中位线DE有什么特殊的关系?证明你的猜想.
解:(2)互相平分,
证明:如图,连接DF,
∵D,E,F分别是AB,AC,BC的中点,
∴AD=EF=AB,AD∥EF,
∴四边形ADFE为平行四边形,
∴中线AF与中位线DE的关系是互相平分.
第5题图
6.如图,四边形ABCD中,一组对边AB=DC=4,另一组对边AD≠BC,对角线BD与边DC互相垂直,M、N、H分别是AD、BC、BD的中点,且∠ABD=30°.求:
(1)MH的长;
解:(1)∵M、H分别是AD、BD的中点,
∴MH∥AB,MH=AB,
∵AB=4,∴MH=2;
第6题图
(2)MN的长.
解:(2)如图,连接HN,过点H作HQ⊥MN于点Q,
同(1)可知,HN∥DC,HN=DC=2,
∴△MHN是等腰三角形,
∵∠ABD=30°,∠BDC=90°,
∴∠MHD=30°,∠NHD=90°,
∴∠MHN=120°,
∴∠HMQ=∠HNQ=30°,
∵MH=2,∴HQ=MH=1,
∴MQ==,
∵HQ⊥MN,∴MN=2MQ=2.
一、填空题
7.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 11 .
第7题图
11
二、解答题
8.如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点,已知两底差是6,两腰和是12,求△EFG的周长.
第8题图
解:如图,连接AE并延长,交CD于点K,
∵AB∥CD,∴∠BAE=∠DKE,
∵点E是BD的中点,∴BE=DE,
在△AEB和△KED中,,
∴△AEB≌△KED(AAS),
∴DK=AB,AE=EK,
∵EF为△ACK的中位线,
∴EF=CK=(DC-DK)=(DC-AB),
∵EG为△BCD的中位线,∴EG=BC,
又∵FG为△ACD的中位线,∴FG=AD,
∴EG+GF=(AD+BC),
∵两腰和是12,∴AD+BC=12,
∵两底差是6,∴DC-AB=6,
∴EG+GF=6,EF=3,
∴△EFG的周长为EG+GF+EF=9.
解答题
9.已知在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC,过AB、DC的中点E、F作直线,直线EF与直线AD、BC分别相交于点M、N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE、HF,根据三角形中位线定理和平行线的性质,判断∠AMF与∠BNE有何数量关系?(不需证明)
解:(1)∠AMF=∠BNE;
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠BNE有何数量关系?请分别写出猜想,并任选一种情况证明.
解:(2)题图2:∠AMF=∠BNE,
证明:如图1,取AC的中点H,连接HE、HF,
∵F是DC的中点,H是AC的中点,
∴HF∥AD,HF=AD,∴∠AMF=∠HFE,
同理,HE∥CB,HE=CB,∴∠BNE=∠HEF,
∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,
∴∠AMF=∠BNE;
图1
图1
题图3:∠AMF+∠BNE=180°,
证明:如图2,取AC的中点H,连接HE、HF,
∵F是DC的中点,H是AC的中点,
∴HF∥AD,HF=AD,∴∠AMF+∠HFE=180°,
同理,HE∥CB,HE=CB,∴∠BNE=∠HEF,
∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,
∴∠AMF+∠BNE=180°.
谢 谢 观 看
第14课时 位似图形
第23章 图形的相似
一、选择题
1. 在△ABC中,AB=AC,∠A=36°,以点A为位似中心,把△ABC放大到原来的2倍后得△AB'C',则∠B'=( C )
A.36° B.54° C.72° D.144°
C
2.如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形,O为位似中心,OD=OD',则A'B'∶AB=( D )
A.2∶3 B.3∶2 C.1∶2 D.2∶1
第2题图
D
二、填空题
3.如图,已知△ABC与△A'B'C'是一对位似三角形,O为位似中心,若AB∶A'B'=3∶1,且OA'=2,则AA'= 4 .
第3题图
4
4. 如图,以O为位似中心,将五边形ABCDE放大得到五边形A'B'C'D'E',已知OA=10cm,OA'=30cm,如果S五边形A'B'C'D'E'=27cm2,那么S五边形ABCDE= 3cm2 .
第4题图
3cm2
三、解答题
5. 在如图所示的方格纸中,按要求作图.(保留作图痕迹)
第5题图
(2)画出以O为位似中心,将△ABC放大到原来的2倍得到的△A2B2C2.
解:(2)如图所示,△A2B2C2即为所求.
(1)画出与△ABC关于直线l对称的图形△A1B1C1;
解:(1)如图所示,△A1B1C1即为所求;
6.如图,在6×8的网格图中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以点O为位似中心,在网格图中作出△A'B'C',使△A'B'C'和△ABC位似,且位似比为1∶2;
解:(1)如图所示,△A'B'C'即为所求;
第6题图
(2)求四边形AA'C'C的周长.(结果保留根号)
解:(2)根据勾股定理,得:
AC==2,
A'C'==,
∴四边形AA'C'C的周长为1++2+2=3+3.
一、填空题
7.若两个位似图形的对应线段长分别为3cm和5cm,且面积之和为68cm2,则较大图形的面积为 50cm2 .
50cm2
二、解答题
8.如图是由边长为1个单位长度的小正方形组成的网格,
(1)以点O为位似中心,在点O的左侧作△A1B1C1,使得它与△ABC的位似比为1∶2;
解:(1)如图所示,△A1B1C1即为所求;
第8题图
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2,并求出点A旋转的路径的长.
解:(2)如图所示,△A2B2C2即为所求,
∵OA==,
∴点A旋转的路径的长为:
=π.
解答题
9.如图,△ABC中,AB=80cm,高CD=60cm,矩形EFGH中,E、F在AB边上,G在BC边上,H在△ABC内,且EF∶GF=2∶1.
第9题图
解:(1)矩形GFEH的位似图形的长与宽的比为2∶1,设其宽IJ=xcm,则长IK=2xcm,
如图,易知△BIJ∽△BCD,△CIK∽△CBA,
∴=①,=②,
①②两式左右两边分别相加得:+=1,
即+=1,解得:x=24,
∴IJ=24cm,∴==,
作法:先找出点I,使=,然后作IJ⊥AB于点J,作IK∥AB交AC于点K,再过点K作KL⊥AB于点L,连接各顶点,四边形IJLK即为所求;
(1)在△ABC内画出矩形GFEH的位似图形,使其顶点在△ABC的边上;(写出作法)
(2)求所作的矩形的面积.
解:(2)由(1)知,该矩形的长IK=48cm,宽IJ=24cm,
∴S矩形IJLK=24×48=1152cm2.
谢 谢 观 看
第15课时 用坐标确定位置
第23章 图形的相似
一、选择题
1.根据下列表述,能确定位置的是( C )
A.北偏东60°
B.成都市春熙路
C.东经118°,北纬40°
D.奥斯卡影院1号厅3排
C
2.下列关于坐标的说法正确的是( D )
A.(3,4)与(4,3)表示的位置相同
B.(a,b)与(b,a)表示的位置肯定不同
C.坐标(4,4)与(4,4)表示两个不同的位置
D.(3,5)与(5,3)是表示不同位置的两个有序数对
D
3.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置为(2,90°)、B的位置为(4,210°),则C的位置为( C )
第3题图
A.(-2,150°) B.(150°,3)
C.(4,150°) D.(3,150°)
C
二、填空题
4.将某会场座位号“7排4号”记作(7,4),那么“3排5号”记作 (3,5) .
5.如图把QQ“笑脸”图标放在直角坐标系中,已知点A的坐标是(-2,3),点B的坐标是(0,3),则嘴唇点C的坐标是 (-1,1) .
(3,5)
(-1,1)
北偏西25°方向,距离为
300m
第5题图
6.学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对于小亮家的位置是 北偏西25°方向,距离为300m .
三、解答题
7.如图所示的是某市市政府周边的一些建筑,以市政府为坐标原点,建立平面直角坐标系(每个小方格的边长为1).
(1)请写出商会大厦和医院的坐标;
解:(1)由图可得:商会大厦的坐标为(-1,2),
医院的坐标为(3,1);
第7题图
(2)王老师在市政府办完事情后,沿(2,0)→(2,-1)→(2,-3)→(0,-3)→(0,-1)→(-2,-1)的路线逛了一下,然后到汽车站坐车回家,写出他路上经过的地方.
解:(2)他路上经过的地方有大剧院,体育公园,购物广场.
8.在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(-3,1)、(-2,-3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
解:(1)如图,根据A(-3,1),B(-2,-3)画出直角坐标系,描出点C(3,2);
第8题图
(2)若同学们打算从点B处直接赶往点C处,请用方向角和距离描述点C相对于点B的位置.
解:(2)BC=5km,
∴点C在点B的东北方向,与点B相距5 km.
一、选择题
9.在一次中学生野外生存训练活动中,每位队员都配发了一张地图,并接到训练任务,要求36小时之内到达目的地,但是,地图上并未标明目的地的具体位置,仅知道A、B两地的坐标分别为A(-1,2)、B(3,2)且目的地与A、B两地的距离分别为5、3,如图所示,则目的地的具体位置的坐标为( B )
第9题图
B
A.(3,5)
B.(3,5)或(3,-1)
C.(-1,-1)或(3,-1)
D.(3,-1)
10.如图,一个粒子在x轴上及第一象限内运动,第1次从(0,0)运动到(1,0),第2次从(1,0)运动到(2,0),第3次从(2,0)运动到(1,1),它接着按图中箭头所示的方向运动,则它第2023次运动到达的点为( C )
第10题图
A.(55,8) B.(56,7)
C.(58,6) D.(59,5)
C
二、填空题
11.如图,在一座高层的商业大厦中,每层的摊位布局基本相同.若第六层的高档服装销售摊位可表示为(6,2,3),则第六层的手表摊位可表示为 (6,4,5) .
第11题图
(6,4,5)
三、解答题
12.象棋在中国有近三千年的历史,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.
(1)若点A的坐标为(-4,4),点B的坐标为(3,1),写出棋子“帅”“马”和“兵”所在点的坐标;
解:(1)由A(-4,4),B(3,1),可知坐标系如图所示,
则帅(1,0)、马(2,3)、兵(-2,1);
第12题图
(2)若“马”的位置在点A,为了到达点B,请按“马”走的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.
解:(2)如图所示,A(-4,4)→(-2,3)→(0,2)→(2,3)→B(3,1).(答案不唯一)
谢 谢 观 看
第16课时 图形的变换与坐标
第23章 图形的相似
一、选择题
1.点P(-2,1)向上平移2个单位后的点的坐标为( A )
A.(-2,3) B.(0,3)
C.(2,-1) D.(0,1)
2.在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(-2,3),则点N的坐标为( C )
A.(-3,2) B.(2,3)
C.(2,-3) D.(-2,-3)
A
C
3.在平面直角坐标系中,若点P(-3,a)与点Q(b,-4)关于x轴对称,则a+b=( C )
A.-7 B.7 C.1 D.-1
4.在平面直角坐标系中,将点A(1,2)绕点P(-1,1)顺时针旋转90°到点A'处,则点A'的坐标为( B )
A.(-2,3) B.(0,-1)
C.(1,0) D.(-3,0)
C
B
二、填空题
5.点M(2,4)先向左平移3个单位长度,再向上平移2个单位长度得到的点的坐标是 (-1,6) .
(-1,6)
三、解答题
6.△ABC与△A'B'C'在平面直角坐标系中的位置如图所示,△A'B'C'是由△ABC经过平移得到的.
(1)分别写出点A',B',C'的坐标;
解:(1)A'(-3,1),B'(-2,-2),C'(-1,-1);
第6题图
(2)说明△A'B'C'是由△ABC经过怎样的平移得到的;
解:(2)△A'B'C'是由△ABC先向左平移4个单位长度,再向下平移2个单位长度得到的;
(3)若点P(a,b)是△ABC内的一点,平移后△A'B'C'内的对应点为P',写出点P'的坐标.
解:(3)平移后△A'B'C'内的对应点P'的坐标为(a-4,b-2).
7.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点A的坐标为(-3,4).
(1)画出与△ABC关于y轴对称的图形△A1B1C1,并写出点A1的坐标;
解:(1)如图所示,△A1B1C1即为所求,A1(3,4);
第7题图
(2)画出将△ABC绕原点O逆时针旋转90°得到的△A2B2C2,并写出点A2的坐标;
解:(2)如图所示,△A2B2C2即为所求,A2(-4,-3);
(3)求出(2)中点A所经过的路径的长度.
解:(3)点A所经过的路径的长度为:
=π.
一、填空题
8.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点B的对应点B'的横坐标是a,则点B的横坐标是 -(a+3) .
第8题图
-(a+3)
二、解答题
9.如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)画出△A'B'C',并写出点A'、B'、C'的坐标;
解:(1)如图所示,△A'B'C'即为所求,
A'(0,4)、B'(-1,1)、C'(3,1);
第9题图
(2)求出△ABC的面积;
解:(2)S△ABC=×(3+1)×3=6;
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
解:(3)设P(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得×4×|y+2|=6,
解得y=1或-5,
∴点P的坐标为(0,1)或(0,-5).
解答题
10.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(7,1)、B(8,2)、C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形;(要求与△ABC在点P的同一侧)
解:(1)如图所示,△A'B'C'即为所求,
第10题图
(2)求线段BC的对应线段B'C'所在直线的解析式.
解:(2)如图,作BD⊥x轴于点D,B'E⊥x轴于点E,
∴B'E∥BD,==,
∵B(8,2),∴OD=8,BD=2,
∵P(12,0),∴OP=12,∴PD=OP-OD=4,
∵△A'B'C'与△ABC的相似比为3,
∴=3,∴==3,∴B'E=6,PE=12,
∵PO=PE,∴点E与点O重合,∴B'(0,6),同理PC'∶PC=3∶1,
又∵PC=OP-OC=3,∴PC'=9,
∴OC'=OP-PC'=3,∴C'(3,0),
设线段B'C'所在直线的解析式为y=kx+b,
则,解得,
∴线段B'C'所在直线的解析式为y=-2x+6.
谢 谢 观 看
第17课时 复习巩固
第23章 图形的相似
一、选择题
1.课间操时,小华、小军、小刚的位置如图所示,如果小军的位置用(0,-2)表示,小刚的位置用(2,0)表示,那么小华的位置可以表示为( A )
第1题图
A
A.(-2,-3) B.(-3,-2)
C.(-3,-4) D.(-4,-3)
2.将点P(m+2,2m+1)向左平移1个单位长度得到点P',且点P'在y轴上,那么点P'的坐标是( A )
A.(0,-1) B.(0,-2)
C.(0,-3) D.(1,1)
A
3.如图,下列条件中不能判定△ACD∽△ABC的是( B )
第3题图
A.∠ADC=∠ACB B.=
C.∠ACD=∠B D.AC2=AD·AB
B
4.如图,△ABC的两条中线BE、CD交于点O,连接DE,则下列结论不正确的是( B )
第4题图
A.= B.S△DOE∶S△BOC=1∶2
C.= D.△ADE∽△ABC
B
二、填空题
5.若===,则= .
6.如图,小雅同学在利用标杆BE测量建筑物的高度时,测得标杆BE高1.2m,又知AB∶BC=1∶8,则建筑物CD的高是 10.8m .
第6题图
10.8m
三、解答题
7.如图,在边长为9的正△ABC中,BD=3,∠ADE=60°,求AE的长.
第7题图
解:∵∠ADE=60°,
∴∠ADB+∠CDE=120°,
∵△ABC是正三角形,
∴∠B=∠C=60°,
∴∠ADB+∠BAD=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,∴=,
∵BD=3,BC=AB=AC=9,
∴CD=BC-BD=6,∴=,
∴CE=2,∴AE=AC-CE=7.
8.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
解:(1)如图,△A1B1C1即为所求;
第8题图
(2)以M为位似中心,在第一象限中画出将△A1B1C1按照2∶1放大后的位似图形△A2B2C2;
解:(2)如图,△A2B2C2即为所求;
(3)△A2B2C2面积为 .
解:(3)14.
一、选择题
9.如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于E,则BE∶EC=( B )
第9题图
A.1∶2 B.1∶3 C.1∶4 D.2∶3
B
二、填空题
10.如图,在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1,过点M1作M1A1⊥OA于点A1;过点A1作A1M2⊥AB于点M2,过点M2作M2A2⊥OA于点A2;…,以此类推,点M2023的坐标为 (1-,) .
第10题图
(1-,)
三、解答题
11.在正方形ABCD中,对角线AC与BD相交于点O,点E是BC边上的一个动点,连接DE,交AC于点F.
(1)如图1,当=时,求的值;
(1)解:∵=,∴=,
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,∴△CEF∽△ADF,
∴=,∴==,∴==;
(2)如图2,当DE平分∠CDB时,求证:AF=OA;
(2)证明:∵DE平分∠CDB,∴∠ODF=∠CDF,
∵AC、BD是正方形ABCD的对角线,
∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,
又∵∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,
∴∠ADF=∠AFD,∴AD=AF,
在Rt△AOD中,AD==OA,
∴AF=OA;
(3)如图3,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=BG.
(3)证明:∵点E是BC的中点,∴=,
由(1)知==,∴=,
又∵FG⊥BC,CD⊥BC,∴FG∥CD,
∴△EGF∽△ECD,∴==,
在Rt△FGC中,∵∠GCF=45°,∴CG=GF,
又∵CD=BC,∴=,=,
∴CG=BG.
谢 谢 观 看
第1课时 成比例线段
第23章 图形的相似
一、选择题
1.如果2a=-3b,那么=( B )
A.- B.- C.5 D.-1
2.下列线段的长度成比例的是( A )
A.1cm、2cm、3cm、6cm
B.2cm、3cm、4cm、5cm
C.1.5cm、2.5cm、4cm、5cm
D.1.1cm、2.2cm、3.3cm、4.4cm
B
A
3.若==(b+d≠0),则的值为( A )
A. B. C.1 D.
4.若a,b,c,d是成比例线段,其中a=3cm,c=6cm,d=4cm,则b的长为( D )
A.8cm B.cm C.4cm D.2cm
A
D
5.若==≠0,则下列各式正确的是( B )
A.2x=3y=4z B.=
C.= D.=
B
二、填空题
6.(1)已知一矩形的长a=1.35m,宽b=60cm,则a∶b= 9∶4 ;
(2)已知点P在线段AB上,且AP∶PB=2∶5,则AB∶PB= 7∶5 ,AP∶AB= 2∶7 .
9∶4
7∶5
2∶7
三、解答题
7.(1)求比例(1-2x)∶(5-x2)=2∶x中的x的值;
解:由比例的性质,得:x(1-2x)=2(5-x2),
∴x-2x2=10-2x2,
∴x=10.
(2)已知==2,求和的值;
解:∵==2,
∴a=2b,c=2d,
∴==,
==.
(3)已知线段a,b,c满足==,且a+2b+c=26.
①求a,b,c的值;
②若线段x是线段6a,b的比例中项,求x的值.
解:①设===k(k≠0),
则a=3k,b=2k,c=6k,
∵a+2b+c=26,
∴3k+2×2k+6k=26,解得k=2,
∴a=3×2=6,
b=2×2=4,
c=6×2=12;
②∵线段x是线段6a,b的比例中项,
∴x2=6ab=6×6×4=144,
∴x=12.
8.若点M在线段AB上,点N在线段BA的延长线上,AB=18,==,求线段MN的长.
解:根据题意画图得:
∵AB=18,==,
∴AM=AB=8,AN=4AB=72,
∴MN=AN+AM=80,
答:线段MN的长为80.
一、选择题
9.若三角形三边长之比为a∶b∶c=3∶4∶5,且a-b+c=12,则这个三角形的周长为( D )
A.12 B.18 C.24 D.36
D
二、填空题
10.正方形ABCD的两条对角线相交于点O,则AO∶AB∶AC= 1∶∶2 .
1∶∶2
三、解答题
11.如图,已知=,AD=6.4cm,DB=4.8cm,EC=4.2cm,求AC的长.
第11题图
解:∵=,
∴=,∴AE=5.6cm,
∴AC=AE+EC=9.8cm.
12.如图,已知Rt△ABC中,∠ACB=90°,BC=8cm,AC=6cm,CD是斜边AB上的高,求CD∶AB的值.
第12题图
解:在Rt△ABC中,由勾股定理得:
AB==10cm,
由面积公式得:
S△ABC=AC·BC=AB·CD,
∴CD==cm,
∴CD∶AB=∶10=.
解答题
13.已知(a+b)∶(b+c)∶(c+a)=7∶14∶9,
(1)求a∶b∶c;
解:∵(a+b)∶(b+c)∶(c+a)=7∶14∶9,
∴设a+b=7k,b+c=14k,c+a=9k,
∴a=k,b=6k,c=8k,
(1)a∶b∶c=1∶6∶8;
(2)求的值.
(2)==-.
谢 谢 观 看
第2课时 平行线分线段成比例
第23章 图形的相似
一、选择题
1.如图,直线a∥b∥c,点A,B在直线a上,点C,D在直线c上,线段AC,BD分别交直线b于点E,F,则下列线段的比值与一定相等的是( B )
第1题图
A. B. C. D.
B
2.如图,已知AD∥BE∥CF,且AB=4,BC=5,EF=4,则DE=( C )
第2题图
A.5 B.3 C.3.2 D.4
C
3.如图,在△ABC中,DE∥BC,AD=5,BD=10,AE=4,则AC=( D )
第3题图
A.8 B.9 C.10 D.12
D
4.如图,在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB=( C )
第4题图
A.3∶8 B.3∶5 C.5∶8 D.2∶5
C
二、填空题
5.如图,已知AB∥CD∥EF,AF、BE相交于O,若AO=OD=DF=3cm,BE=10cm,则BO的长为 cm .
第5题图
cm
6.如图,已知a∥b∥c,AC∶CO∶OF=2∶1∶4,BE=35,那么BD= 10 .
第6题图
10
三、解答题
7.如图,已知AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若=,DE=6,求EF的长.
第7题图
解:∵AD∥BE∥CF,
∴=,
∵=,DE=6,
∴=,∴EF=9.
8.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)若AD=5,DB=6,EC=12,求AE的长;
解:(1)∵DE∥BC,
∴=,即=,
解得AE=10;
第8题图
(2)若AB=10,AD=4,AE=6,求EC的长.
解:(2)∵DE∥BC,
∴=,即=,
解得AC=15,
∴EC=AC-AE=9.
一、填空题
9.如图,在△ABC中,AB=AC,F为BC的三等分点,EF⊥BC交AB于E,若BE=2,则AB= 3 .
第9题图
3
二、解答题
10.如图,已知点O是△ABC中BC边的中点,且=,求的值.
第10题图
解:如图,过点B作BF∥AC交DE于点F,
∵BF∥AC,
∴∠FBO=∠C,∠BFO=∠CEO,
∵O为BC的中点,
∴BO=CO,
在△OBF和△OCE中,
,
∴△OBF≌△OCE(AAS),∴BF=CE,
∵=,∴=,
又∵BF∥AE,
∴==,
∴=,
∴==.
解答题
11.请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA,交BA的延长线于E,….
(1)请按照上面的证明思路,写出该证明的剩余部分;
(1)证明:如图2,过C作CE∥DA,交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,∴∠ACE=∠E,
∴AE=AC,∴=;
(2)如图3,已知在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
(2)解:∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,∴=,即=,
∴BD=BC=,
∴AD==,
∴C△ABD=AB+BD+AD=.
谢 谢 观 看
第3课时 专题黄金分割
第23章 图形的相似
一、选择题
1. 如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽、AB为长的矩形面积为S2,则S1与S2之间的大小关系为( A )
A.S1=S2
B.S1>S2
C.S1<S2
D.不能确定
第1题图
A
2.若点C是线段AB的黄金分割点,AB=8cm,AC>BC,则AC的长为( C )
A.cm B.2(-1)cm
C.4(-1)cm D.6(-1)cm
3.已知线段AB=1,C是AB的黄金分割点,AC>BC,则BC的长为( C )
A.-1 B. C. D.
4.在长度为1的线段上找到两个黄金分割点P,Q,则PQ=( D )
A. B. C.3- D.-2
C
C
D
二、填空题
5.把10米长的线段进行黄金分割,则分成的较长的线段长为 (5-5) 米.
6.点C是线段AB上的黄金分割点(AC>BC),若AC=+1,则BC的长是 2 .
(5-5)
2
三、解答题
7.若线段AB=4cm,点C是线段AB的黄金分割点,AC>BC,求AC-BC的值.
解:∵点C是线段AB的黄金分割点,AC>BC,
∴AC=AB=(2-2)cm,
∴BC=AB-AC=(6-2)cm,
∴AC-BC=(4-8)cm.
8.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长xcm与身高lcm的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为多少?(精确到1cm)
第8题图
解:由题意得x=165×0.60=99,
设需要穿的高跟鞋的高度是ycm,
则根据黄金分割的定义,
得=0.618,解得y≈8,
答:她应穿的高跟鞋的高度大约为8cm.
9.如图,△ABC是顶角为36°的等腰三角形,已知底与腰的比为的三角形是黄金三角形,若△ABC、△BDC、△DEC都是黄金三角形,且AB=4,求DE的长.
第9题图
解:∵△ABC是黄金三角形,
∴BC=AB=2-2,
∵△BCD是黄金三角形,
∴CD=BC=6-2,
∵△DEC是黄金三角形,
∴DE=CD=6-2,
即DE的长为6-2.
一、填空题
10.著名数学家华罗庚(1910-1985)倡导优选法,就是对生产和科学试验中提出的问题,根据数学原理,通过尽可能少的试验次数,迅速求得最佳方案的方法.这个数学原理就是利用中国古代黄金分割比值的近似值0.618乘以任意一个数,所得的另一个数,就是最佳的方案.某医院急诊室的护士利用体温表给病人量体温,按常规测一次体温需3分钟时间,实际上是 1.854 分钟时测的体温,同3分钟时测的体温一样,这 1.854 分钟与 1.146 分钟之间的分界点,就是用优选法产生出来的.
1.854
1.854
1.146
二、解答题
11.如果一个矩形的宽与长的比值为,那么称这个矩形为黄金矩形.如图,将矩形ABCD剪掉一个正方形ADFE后,剩余的矩形BCFE(BC>BE)是黄金矩形,则原矩形ABCD是否为黄金矩形?请说明理由.
第11题图
解: 原矩形ABCD是黄金矩形,
理由: 设矩形BCFE的长BC=x,
∵矩形BCFE为黄金矩形,
∴宽BE=x,
∵四边形AEFD是正方形,
∴AE=EF=BC=x,
∴AB=x+x=x,
∴==,
∴原矩形ABCD是黄金矩形.
解答题
12.如图,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(1)解:在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF-PA=PD-PA=-1,
DM=AD-AM=2-(-1)=3-;
第12题图
(2)求证:AM2=AD·DM;
(2)证明:∵AM2=(-1)2=6-2,AD·DM=2(3-)=6-2,
∴AM2=AD·DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
(3)解:∵AM2=AD·DM,==,
∴点M是AD的黄金分割点.
谢 谢 观 看
第4课时 相似图形
第23章 图形的相似
一、选择题
1.下列说法正确的是( C )
A.菱形都是相似图形
B.各边对应成比例的多边形是相似多边形
C.等边三角形都是相似三角形
D.矩形都是相似图形
C
2.若五边形ABCDE∽五边形A1B1C1D1E1,且=3,则五边形A1B1C1D1E1与五边形ABCDE的相似比是( B )
A.3∶1 B.1∶3
C.1∶9 D.无法确定
3.已知矩形ABCD中,AB=4,BC=3,下列矩形与矩形ABCD相似的是( A )
A. B.
C. D.
B
A
二、填空题
4.一个四边形的各边长之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为 20 cm.
5. ABCD和 EFGH中,AB=3,BC=5,∠B=40°,EF=6,要使 ABCD∽ EFGH,则FG= 10 ,∠F= 40° .
6.如图,已知四边形ABCD与四边形A'B'C'D'相似,则∠B'= 60° .
20
10
40°
60°
第6题图
三、解答题
7.如图,等腰梯形ABCD与等腰梯形A'B'C'D'相似,∠A'=65°,A'B'=6cm,AB=8cm,AD=5cm,试求梯形ABCD的各角的度数与A'D',B'C'的长.
第7题图
解:∵等腰梯形ABCD与等腰梯形A'B'C'D'相似,∠A'=65°,
∴∠A=∠A'=65°,∠B=∠A=65°,∠D=∠C=180°-65°=115°,
∵等腰梯形ABCD与等腰梯形A'B'C'D'相似,
∴=,即=,
∴A'D'=cm,
∴B'C'=A'D'=cm.
8.如图,有一块长为2m、宽为1m的矩形玻璃ABCD,为了保护玻璃,需要镶上宽10cm的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?
第8题图
解:不相似,理由如下:
∵AB=2m,AD=1m,
∴EF=2-0.1×2=1.8m,
∴EN=1-0.1×2=0.8m,
∴==0.9,==0.8,
∵≠,
∴边框的内外边缘所成的矩形不相似.
一、填空题
9.下列说法正确的有 ②④ .(填序号)
①在两个边数相同的多边形中,如果各对应边成比例,那么这两个多边形相似;②两个矩形有一组邻边对应成比例,这两个矩形相似;③有一个角对应相等的平行四边形都相似;④有一个角对应相等的菱形都相似.
10.将一张报纸对折后,若对折后的半张报纸和整张报纸相似,则整张报纸的长和宽的比是 ∶1 .
②④
∶1
二、解答题
11.如图,矩形花坛ABCD的宽AB=20米,长AD=30米.现计划在该花坛四周修筑小路,使小路四周所围成的矩形A'B'C'D'与矩形ABCD相似,并且相对的两条小路的宽相等,试问小路的两个宽x与y的比值是多少?
第11题图
解:根据题意得A'B'=AB+2y,A'D'=AD+2x,
∵矩形A'B'C'D'∽矩形ABCD,
∴A'B'∶A'D'=AB∶AD,
∴(20+2y)∶(30+2x)=20∶30,
∴=,
即小路的两个宽x与y的比值是.
解答题
12.已知矩形ABCD中,AD=3,AB=1.
(1)若EF把矩形分成两个小的矩形,如图所示,其中矩形ABEF与矩形ABCD相似,求AF∶AD;
解:(1)设AF=x,
∵矩形ABEF与矩形ABCD相似,AD=3,AB=1,
∴=,即=,解得x=,
∴AF∶AD=∶3=1∶9;
第12题图
(2)若在矩形ABCD内不重叠地放两个长是宽的3倍的小矩形,且每个小矩形的每条边与矩形ABCD的边平行,求这两个小矩形的周长和的最大值.
解:(2)两个小矩形的放置情况有如下几种:
①如图1,两个小矩形都“竖放”,
在这种放法下,周长和最大的两个小矩形,两边长分别为1和 ,
此时两个小矩形的周长和的最大值为 ;
第12题图
图1
图1
②如图2、图3,两个小矩形都“横放”,
此时两个小矩形的周长和的最大值为:
2(a+3a)+2[1-a+3(1-a)]=8;
图2
图3
图2
图3
③如图4,两个小矩形一个“横放”,一个“竖放”,
此时两个小矩形的周长和为:
2(a+3a)+2(3-a+)=8+,
∵0<3a≤1,即0<a≤,
∴当a=时,两个小矩形的周长和最大,为 ,
综上所述,这两个小矩形的周长和的最大值为.
图4
图4
谢 谢 观 看
第5课时 相似三角形
第23章 图形的相似
一、选择题
1.(1)已知△ABC∽△DEF,AB∶DE=3∶1,AB=6,则DE的长为( B )
A.18 B.2 C.54 D.
(2)已知△ADE∽△ABC,且相似比为,若DE=8,则BC的长是( D )
A. B.6 C.8 D.12
B
D
2.如图,在△ABC中,DE∥BC,AD=3BD,DE=3,则BC的长为( C )
第2题图
A.1 B. C.4 D.6
C
3.如图,AB∥CD,若AB=12,CD=4,AO=9,则CO的长是( B )
第3题图
A. B.3 C.4.5 D.6
B
二、填空题
4.若△ABC∽△A'B'C',∠A=50°,∠C=110°,则∠B'的度数为 20° .
5.如图,在△ABC中,AB=4,AC=3,D是AB边上的一点,若△ABC∽△ACD,则AD的长为 .
第5题图
20°
6.如图,AB∥CD,AC,BD,EF相交于点O,则图中相似的三角形共有 3 对.
第6题图
3
三、解答题
7.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
第7题图
解:∵△ADE∽△ABC,
∴==,
∵DE=4,BC=12,CD=9,AD=3,
∴AC=AD+CD=12,
∴==,
∴AE=4,AB=9,
∴BE=AB-AE=5.
8.如图,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:
(1)∠AED和∠ADE的度数;
解:(1)∵DE∥BC,∠C=40°,
∴∠AED=∠C=40°,
∵∠A=45°,
∴∠ADE=180°-∠A-∠AED=95°;
第8题图
(2)DE的长.
解:(2)∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵AE=50cm,EC=30cm,BC=70cm,
∴=,
∴DE=cm.
一、填空题
9.如图,在矩形ABCD中,作DF⊥AC,垂足为F,延长DF交边AB于点E,在图中一定和△DFC相似的三角形有 5 个.
第9题图
5
10.如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则的值是 .
第10题图
二、解答题
11.如图,在 ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,求AC的长.
第11题图
解:如图,延长FE交CB的延长线于点H,
∵四边形ABCD是平行四边形,
∴BC=AD=AF+DF=6cm,BC∥AD,
∴∠EAF=∠EBH,∠AFE=∠BHE,
∵E为AB的中点,∴AE=BE,
∴△AFE≌△BHE(AAS),
∴BH=AF=2cm,∴CH=BH+BC=8cm,
∵BC∥AD,
∴AG∶CG=AF∶CH,
即3∶CG=2∶8,∴CG=12cm,
∴AC=AG+CG=15cm.
解答题
12.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
①当=时,=;
②当=时,=;
③当=时,=;
….
猜想当=时,的值,并说明理由.
第12题图
解:猜想:当=时,=,理由如下:
如图,过点D作DG∥BE,交AC于点G,
则==,
∴=,∴EG=nAE,
∵AD是△ABC的中线,且DG∥BE,
∴EG=CG,∴AC=(2n+1)AE,
∴=.
谢 谢 观 看
第6课时 相似三角形的判定(1)
第23章 图形的相似
一、选择题
1.下列条件中,一定能判断两个等腰三角形相似的是( C )
A.都含有一个40°的内角
B.都含有一个50°的内角
C.都含有一个60°的内角
D.都含有一个70°的内角
C
2.如图,在△ABC中,D,E分别为AC、BC边上的点,若∠1=∠2=∠3,则图中相似的三角形共有( D )
第2题图
A.1对 B.2对 C.3对 D.4对
D
3.如图,在△ABC中,D、E分别为AB、AC边上的点,且∠AED=∠B,AD=3,AC=6,DB=5,则AE的长度为( D )
第3题图
A. B. C. D.4
D
二、填空题
4.如图,要使△ABC∽△ACD,需补充的条件是 ∠ACD=∠B(或∠ADC=∠ACB) .(写出一种即可)
第4题图
∠ACD=∠B(或∠ADC=
∠ACB)
5.如图,D为△ABC的AB边上的一点,∠DCA=∠B,若AC=cm,AB=3cm,则AD的长为 2cm .
第5题图
2cm
三、解答题
6.如图,点D,E在BC上,且FD∥AB,FE∥AC,求证:△ABC∽△FDE.
第6题图
证明:∵FD∥AB,FE∥AC,
∴∠B=∠FDE,∠C=∠FED,
∴△ABC∽△FDE.
7.如图,已知△PQR是等边三角形,∠APB=120°,求证:△PAQ∽△BPR.
第7题图
证明:∵△PQR是等边三角形,
∴∠PQR=∠PRQ=60°,
∴∠PQA=∠BRP=120°,
∵∠PQR是△PQA的外角,
∴∠PQR=∠APQ+∠PAQ=60°,
∵∠APB=120°,
∴∠PAQ+∠PBR=60°,
∴∠APQ=∠PBR,
∴△PAQ∽△BPR.
8.如图,在 ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
第8题图
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠C+∠D=180°,∠BAF=∠AED,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
一、填空题
9.如图,直线y=-2x+4与x轴,y轴分别相交于A,B两点,C为OB上一点,若∠1=∠2,则S△ABC= 3 .
第9题图
3
10.如图,在 ABCD中,AD=10cm,CD=6cm,E为AD上一点,若BE=BC,CE=CD,则DE= 3.6 cm.
第10题图
3.6
二、解答题
11.如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.
(1)求证:△COM∽△CBA;
(1)证明:∵A与C关于直线MN对称,
∴AC⊥MN,∠COM=90°,
在矩形ABCD中,∠B=90°,
∴∠COM=∠B,
又∵∠MCO=∠ACB,
∴△COM∽△CBA;
第11题图
(2)求线段OM的长.
(2)解:∵在Rt△CBA中,AB=6,BC=8,
∴AC==10,∴OC=5,
∵△COM∽△CBA,
∴=,即=,
∴OM=.
解答题
12.如图,已知正方形DEFG内接于Rt△ABC,EF在斜边BC上,EH⊥AB于H,求证:
(1)△ADG≌△HED;
证明:(1)如图,
∵四边形DEFG为正方形,
∴∠EDG=90°,DG=ED,
∴∠1+∠2=90°,
∵EH⊥AB,
∴∠2+∠3=90°,
∴∠1=∠3,
∵∠A=∠EHD=90°,DG=ED,
∴△ADG≌△HED(AAS);
第12题图
(2)EF2=BE·FC.
证明:(2)∵四边形DEFG为正方形,
∴∠DEF=∠EFG=90°,DE=GF=EF,
∴∠DEB=∠CFG=90°,
在Rt△ABC中,∠B+∠C=90°,
在Rt△BDE中,∠B+∠2=90°,
∴∠2=∠C,
∴△BDE∽△GCF,
∴=,
∵DE=GF=EF,
∴=,
∴EF2=BE·FC.
谢 谢 观 看
第7课时 相似三角形的判定(2)
第23章 图形的相似
一、选择题
1.下列条件中,不能判定△ABC和△DEF相似的是( D )
A.∠A=∠D=70°,∠B=60°,∠E=50°
B.∠A=∠D=70°,∠C=50°,∠E=50°
C.∠A=∠D=70°,AB=12cm,AC=15cm,ED=16cm,DF=20cm
D.∠A=∠D=70°,AB=12cm,AC=15cm,ED=16cm,EF=20cm
D
2.如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( D )
第2题图
A.AB∥CD B.∠A=∠D
C.= D.=
D
二、填空题
3.如图,若= ,则△OAC∽△OBD.
第3题图
4.如图,△ABC中,D为AB上一点,若AC2=AD·AB,则△ABC∽ △ACD .
第4题图
△ACD
5.如图,在四边形ABCD中,已知∠A=∠CBD,AB=15cm,AD=20cm,BD=18cm,BC=24cm,则CD的长为 cm.
第5题图
三、解答题
6.如图,已知∠BAE=∠CAD,AB=18,AC=48,AE=15,AD=40,求证:△ABC∽△AED.
第6题图
证明:∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,
即∠BAC=∠EAD,
∵AB=18,AC=48,AE=15,AD=40,
∴==,
∴△ABC∽△AED.
7.如图,在△ABC中,BD⊥AC于点D,DE⊥AB于点E,BD·DE=BE·CD,求证:△BCD∽△BDE.
第7题图
证明:∵BD⊥AC,DE⊥AB,
∴∠BDC=∠BED=90°,
∵BD·DE=BE·CD,
∴=,
∴△BCD∽△BDE.
8.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,△ABC和△DEF的顶点都在边长为1的小正方形的格点上.
(1)∠ABC= °,BC= ;
解:(1)135,2;
第8题图
(2)判断△ABC与△DEF是否相似,若相似,请说明理由.
解:(2)△ABC∽△DEF.理由如下:
∵AB=2,BC=2,DE=,EF=2,
∴==,
又∵∠ABC=∠DEF=135°,
∴△ABC∽△DEF.
一、填空题
9.如图,∠A=∠B=90°,AB=7,BC=3,AD=2,在边AB上取点P,使得△PAD与△PBC相似,则满足条件的AP长为 2.8或1或6 .
第9题图
2.8或1或6
二、解答题
10.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CF=3FD.
(1)求证:△ABE∽△DEF;
(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴==2,==2,
∴=,
又∵∠A=∠D=90°,
∴△ABE∽△DEF;
第10题图
(2)△ABE与△EBF相似吗?为什么?
(2)解:△ABE∽△EBF,理由如下:
∵△ABE∽△DEF,
∴==,∠ABE=∠DEF,
∵∠AEB+∠ABE=90°,
∴∠AEB+∠DEF=90°,∴∠BEF=90°,
又∵=,∠A=90°,
∴==,∠A=∠BEF=90°,
∴△ABE∽△EBF.
解答题
11.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,P、Q两点同时出发,设移动时间为ts.
(1)当t为何值时,△PBQ是等腰三角形?
(1)∵△PBQ是等腰三角形,∠B=90°,
∴BP=BQ,即6-t=2t,解得t=2,
∴当t=2时,△PBQ是等腰三角形;
第11题图
解:由题意得BP=(6-t)cm,BQ=2tcm,
(2)当t为何值时,△PBQ的面积为5cm2?
(2)S△PBQ=BP·BQ=(6-t)·2t=5,
即(t-1)(t-5)=0,解得t=1或5,
∴当t=1或5时,△PBQ的面积为5cm2;
(3)当t为何值时,△PBQ和△ABC相似?
(3)①若△BPQ∽△BAC,则=,
即=,解得t=3;
②若△BPQ∽△BCA,则=,
即=,解得t=1.2,
综上所述,当t=3或1.2时,△PBQ和△ABC相似.
谢 谢 观 看
第8课时 相似三角形的判定(3)
第23章 图形的相似
一、选择题
1.甲三角形的三边长分别为9,6,12,乙三角形的三边长分别为4,6,8,则这两个三角形( C )
A.一定不相似 B.不一定相似
C.一定相似 D.无法判断是否相似
C
2.在下列条件中,不能判断△ABC与△DEF相似的是( B )
A.==
B.=且∠B=∠E
C.=且∠A=∠D
D.∠A=∠D,∠B=∠E
B
3.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与如图所示的△ABC相似的三角形所在的网格图形是( B )
第3题图
A
B
C
D
B
二、填空题
4.已知在△ABC中,AB=4,BC=5,CA=6.
(1)如果DE=10,那么当EF= 12.5 ,FD= 15 时,△DEF∽△ABC;
(2)如果DE=10,那么当EF= 12 ,FD= 8 时,△FDE∽△ABC.
5.在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,则当= 2 时,△ABC∽△DEF.
12.5
15
12
8
2
三、解答题
6.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
(1)AB=12,BC=15,AC=24,A'B'=25,B'C'=40,C'A'=20;
解:(1)△ABC∽△C'A'B',理由如下:
∵==,==,==,
∴==,
∴△ABC∽△C'A'B';
(2)AB=3,BC=4,AC=5,A'B'=12,B'C'=16,C'A'=20.
解:(2)△ABC∽△A'B'C',理由如下:
∵==,==,==,
∴==,
∴△ABC∽△A'B'C'.
7.如图,在由边长为1的小正方形组成的网格中有A、B、C、D、E五个点,问△ABC与△ADE是否相似?为什么?
第7题图
解:△ABC∽△ADE,理由如下:
由图可知,AB==2,BC=10,
AC==2,AE=2,AD=,
DE==,
∴===,
∴△ABC∽△ADE.
一、填空题
8.如图,在Rt△ABC和Rt△ACD中,∠ACB=∠ADC=90°,AC=,AD=2,则当AB= 3或3 时,△ABC与△ACD相似.
第8题图
3或3
9.如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为 3 .
第9题图
3
二、解答题
10.如图,点B、D、E在同一条直线上,BE与AC相交于点F,==.
(1)求证:∠BAD=∠CAE;
(1)证明:∵==,
∴△ABC∽△ADE,∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,
∴∠BAD=∠CAE;
第10题图
(2)若∠BAD=21°,求∠EBC的度数;
(2)解:∵△ABC∽△ADE,
∴∠ABC=∠ADE,
∵∠ABC=∠ABE+∠EBC,
∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=21°;
(3)连接EC,求证:△ABD∽△ACE.
(3)证明:由(1)知∠BAD=∠CAE,
又∵=,即=,
∴△ABD∽△ACE.
解答题
11.如图,在平面直角坐标系中,梯形OABC的边OA在x轴上,OC在y轴上,OA∥BC,点E在对角线OB上,点D在OC上,直线DE与x轴交于点F,已知OE=2EB,CB=3,OA=6,BA=3,OD=5.
第11题图
(1)证明:如图,过点B作BG⊥OA于点G,
∴四边形OCBG是矩形,
∴BG=OC,OG=BC=3,AG=OA-OG=3,
由勾股定理,得BG==6,
∴OC=BG=6,
由勾股定理,得OB==3,
∵OE=2EB,∴OE=OB=2,
∵==,且∠DOE=∠BOC,
∴△ODE∽△OBC;
(1)求证:△ODE∽△OBC;
(2)在y轴上找一点P,使得△PFO∽△ODE,直接写出点P的坐标.
(2)解:∵△ODE∽△OBC,
∴∠OED=∠OCB=90°,
∴∠OED=∠FOD=90°,DE==,
又∵∠ODE=∠FDO,∴△DOE∽△DFO,
∴=,即=,∴FO=10,
∵△PFO∽△ODE,
∴=,即=,∴PO=20,
∴点P的坐标为(0,20)或(0,-20).
谢 谢 观 看
第9课时 专题相似三角形的判定
第23章 图形的相似
解答题
1. 如图,在△ABC中,∠C=90°,DE⊥AB于点E,DF⊥BC于点F,DF交AB于点H,求证:△DEH∽△BCA.
第1题图
证明:∵DE⊥AB,DF⊥BC,
∴∠D+∠DHE=∠B+∠BHF=90°,
∵∠BHF=∠DHE,
∴∠D=∠B,
又∵∠DEH=∠C=90°,
∴△DEH∽△BCA.
2.如图,点D在△ABC的边AB上,AD=1,BD=2,AC=,求证:△ACD∽△ABC.
第2题图
证明:∵==,=,
∴=,
∵∠A=∠A,
∴△ACD∽△ABC.
3.如图,△ABC中,D、E分别在边AB、AC上,AD=2BD,AE=2CE,=,求证:△ABC与△ADE相似.
第3题图
证明:∵AD=2BD,AE=2CE,
∴=,=,
∵=,
∴==,
∴△ADE∽△ABC.
4.如图,在矩形ABCD中,BC=12cm,AB=8cm,P、Q分别是AB、BC上的两动点.若点P自点A出发,以1cm/s的速度沿AB方向运动,同时,点Q自点B出发,以2cm/s的速度沿BC方向运动,问经过几秒,△PBQ与△BCD相似?
第4题图
解:如图,
设经过xs,△PBQ与△BCD相似,
则AP=xcm,PB=(8-x)cm,BQ=2xcm,
由于∠PBQ=∠BCD=90°,
①当∠1=∠2时,△PBQ∽△DCB,
∴=,即=,
解得x=;
②当∠1=∠3时,△PBQ∽△BCD,
∴=,即=,
解得x=2,
∴经过s或2s,△PBQ与△BCD相似.
解答题
5.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(1)证明:由勾股定理得:AB2=22+42=20,AC2=22+12=5,BC2=32+42=25,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
第5题图
(2)判断△ABC和△DEF是否相似,并说明理由;
(2)解:△ABC与△DEF相似,
理由:由勾股定理得:DF==2,DE==4,EF==2,
由(1)知:AB=2,AC=,BC=5,
∴===,
∴△ABC∽△DEF;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
(3)解:如图,和△ABC相似的三角形是△P4P5P2,
理由:由勾股定理得:P5P2==,P4P2==,P4P5==2,
∵AB=2,AC=,BC=5,
∴===,
∴△ABC∽△P4P5P2.
解答题
6.如图,在平面直角坐标系xOy内,点A(6,0)、C(-4,0),过点A作直线AB,交y轴的正半轴于点B,且AB=10,点P是直线AB上的一个动点.
(1)求点B的坐标和直线AB的表达式;
解:(1)∵A(6,0),∴OA=6,
∴OB==8,
∵点B在y轴的正半轴,
∴点B的坐标为(0,8),
设直线AB的表达式为y=kx+b(k≠0),
将A(6,0),B(0,8)代入y=kx+b,
得,解得,
∴直线AB的表达式为y=-x+8;
第6题图
(2)若△APC与△AOB相似,求点P的坐标.
解:(2)如图,分两种情况考虑,
①当△AOB∽△ACP1时,∠ACP1=∠AOB=90°,
∵当x=-4时,y=-x+8=,
∴点P1的坐标为(-4,);
②当△AOB∽△AP2C时,设P2(m,-m+8),
∵A(6,0),C(-4,0),∴AC=10,
∵△AOB∽△AP2C,∴=,即=,
解得CP2=8,
∴=8,
整理,得:(m-4)2=0,解得m=,
∴点P2的坐标为(,),
综上所述,点P的坐标为(-4,)或(,).
谢 谢 观 看
第10课时 相似三角形的性质
第23章 图形的相似
一、选择题
1.若两个相似三角形的相似比是2∶5,则对应高的比是( A )
A.2∶5 B.4∶25 C. D.25∶4
2.已知两个相似三角形的相似比是2∶3,其中较小三角形的一条中线长6cm,则较大三角形中对应的中线长为( D )
A.4cm B.6cm C.8cm D.9cm
3.若两个相似三角形的面积之比为1∶9,则它们的周长之比为( A )
A.1∶3 B.3∶1 C.1∶9 D.9∶1
A
D
A
二、填空题
4.两个相似三角形对应边上中线的比为3∶2,则对应边上的高的比为 3∶2 ,周长之比为 3∶2 ,面积之比为 9∶4 .
5.如果两个相似三角形对应角平分线的比是2∶3,它们一条对应高的差为5cm,那么这两条对应高的长分别是 10cm,15cm .
6.已知两个相似三角形的相似比为2∶5,其中较小的三角形面积是4,那么另一个三角形的面积为 25 .
3∶2
3∶2
9∶4
10cm,15cm
25
三、解答题
7.已知△ABC∽△A'B'C',=,AB边上的中线CD=4cm,△ABC的周长为20cm,△A'B'C'的面积是64cm2,求:
(1)A'B'边上的中线C'D'的长;
解:(1)∵△ABC∽△A'B'C',=,
∴=,
∴C'D'=4×2=8cm,
∴A'B'边上的中线C'D'的长为8cm;
(2)△A'B'C'的周长;
解:(2)∵△ABC∽△A'B'C',=,
∴=,
∴C△A'B'C'=20×2=40cm,
∴△A'B'C'的周长为40cm;
(3)△ABC的面积.
解:(3)∵△ABC∽△A'B'C',=,
∴==,
∴S△ABC=64÷4=16cm2,
∴△ABC的面积是16cm2.
8.如图,在△ABC中,BC=120mm,点Q,M在BC上,点P,N分别在AB,AC上,四边形PQMN为矩形,△ABC的高AD与PN相交于点E,且AD=80mm.
(1)若这个矩形是正方形,则边长是多少?
解:(1)设正方形PQMN的边长为xmm,
∵四边形PQMN为正方形,
∴PN∥QM,∴△APN∽△ABC,
∴=,即=,
解得x=48,
∴正方形PQMN的边长是48mm;
第8题图
(2)若这个矩形的长是宽的2倍,则长和宽各是多少?
解:(2)设矩形PQMN的宽为ymm,
由(1)得△APN∽△ABC,
∴=,即=,或=,
解得y=30或,
∴矩形PQMN的宽为30mm,长为60mm或宽为mm,长为mm.
一、填空题
9.如图,在 ABCD中,E为CD上一点,DE∶CE=2∶3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF∶S△EBF∶S△ABF= 4∶10∶25 .
第9题图
4∶10∶25
10.如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,…,如此作下去,则所作的第n个正方形的面积Sn= .
第10题图
二、解答题
11.如图,四边形ABCD中,AD∥BC,∠ACD=∠B,求证:=.
第11题图
证明:∵AD∥BC,∴∠ACB=∠DAC,
∵∠ACD=∠B,∴△ACB∽△DAC,
∴=()2,
又∵AD∥BC,∴=,
∴()2=,即=.
解答题
12.如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A,C不重合)在AC边上,EF∥AB交BC于点F.试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若存在,请求出EF的长;若不存在,请简要说明理由.
第12题图
解:存在.
∵EF∥AB,∴△ECF∽△ACB,
△EFP为等腰直角三角形,有三种情况:
①如图1,过点C作CD⊥AB于点D,
当∠PEF=90°,EP=EF时,
由AB=5,BC=3,AC=4,得∠ACB=90°,
∴Rt△ACB斜边AB上的高CD=,
设EP=EF=x,
由△ECF∽△ACB,得:=,
即=,解得x=,即EF=;
图1
②如图1,当∠EFP'=90°,EF=FP'时,
同①理可得EF=;
图1
③如图2,当∠EP″F=90°,P″E=P″F时,
过点P″作P″H⊥EF于点H,过点C作CD⊥AB于点D,
∴P″H=EF,
设EF=x,则P″H=x,
由△ECF∽△ACB,得:=,
即=,解得x=,即EF=,
综上所述,在AB上存在点P,使得△EFP为等腰直角三角形,此时EF=或.
图2
谢 谢 观 看
第11课时 专题比例线段的证明
第23章 图形的相似
解答题
1.如图,在△ABC与△DBE中,∠A=∠D,∠ABD=∠CBE.求证:BD·BC=BA·BE.
第1题图
证明:∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,
∵∠A=∠D,∴△ABC∽△DBE,
∴=,∴BD·BC=BA·BE.
2.如图,在 ABCD中,M,N分别是AD,BC上的点,ME⊥BD,NF⊥BD,垂足分别是E,F,求证:=.
第2题图
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠MDE=∠NBF,
∵ME⊥BD,NF⊥BD,
∴∠MED=∠NFB=90°,
∴△MED∽△NFB,∴=.
3.如图,在Rt△ABC中,∠C=90°,点E,F在AB上,点D,G分别在BC,AC上,且四边形DEFG是正方形,求证:EF2=BE·AF.
第3题图
证明:∵∠C=90°,
∴∠A+∠B=90°,
∵四边形DEFG是正方形,
∴∠AFG=∠DEB=90°,GF=EF=DE,
∴∠A+∠AGF=90°,∴∠AGF=∠B,
∴△AFG∽△DEB,∴=,即=,
∴EF2=BE·AF.
4.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,求证:AE·AB=AF·AC.
第4题图
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵DE⊥AB,
∴∠AED=∠ADB=90°,
又∵∠BAD=∠DAE,
∴△ABD∽△ADE,
∴=,∴AD2=AE·AB,
同理:AD2=AF·AC,
∴AE·AB=AF·AC.
5.如图,在△ABC中,AM是BC边上的中线,直线DN∥AM,交AB于点D,交CA的延长线于点E,交BC于点N.求证:=.
第5题图
证明:∵直线DN∥AM,∴=,=,
∵在△ABC中,AM是BC边上的中线,
∴MB=MC,∴=.
6.如图,已知△ABC中,D为AC上一点,E为CB延长线上一点,BE=AD,ED和AB相交于点F,求证:EF∶FD=AC∶BC.
第6题图
证明:如图,过点D作DG∥BC,交AB于点G,
则△ADG∽△ACB,△DGF∽△EBF,
∴=,=,∴=,
∵BE=AD,∴==,
即EF∶FD=AC∶BC.
解答题
7.在四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,∴∠ADE+∠DFC=90°,
∴∠AED=∠DFC,∴△ADE≌△DCF(AAS),∴DE=CF;
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:=;
(2)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,∴∠DCF+∠CFD=90°,
∵DE⊥CF,∴∠ADE+∠CFD=90°,∴∠ADE=∠DCF,
∴△ADE∽△DCF,∴=;
(3)如图3,若四边形ABCD是平行四边形,试探究:当∠B与∠EGF满足什么关系时,=成立?并证明你的结论.
(3)解:当∠B=∠EGF时,=成立,
证明:如图,在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM,
∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠A=∠CDM,∠B+∠A=180°,
∵∠B=∠EGF,∴∠EGF+∠A=180°,
∴∠AED=∠CFM=∠CMF,∴△ADE∽△DCM,
∴=,即=.
解答题
8.如图1,△ABC中,∠ACB=90°,射线CD⊥AB于点D.点P是射线CD上一动点,连接AP并在AP边右侧作△APQ,使得∠PAQ=∠CAB且=,连接BQ.
(1)求证:BA平分∠CBQ;
(1)证明:∵CD⊥AB,∠ACB=90°,
∴∠CAB+∠ABC=∠CAB+∠ACD=90°,
∴∠ACD=∠ABC,
∵∠PAQ=∠CAB,=,
∴∠PAC=∠QAB,=,
∴△CAP∽△BAQ,∴∠ACP=∠ABQ,
∴∠ABC=∠ABQ,∴BA平分∠CBQ;
(2)当AQ∥BC时,如图2,延长AP交BC边于点E,求证:CE·BC=AD·AB;
(2)证明:∵AQ∥BC,∴∠QAB=∠CBA,
由(1)得∠CAE=∠QAB,∴∠CAE=∠CBA,
又∵∠ACE=∠BCA=90°,∴△ACE∽△BCA,
∴=,∴AC2=CE·BC,
∵∠CAD=∠BAC,∠ACD=∠ABC,
∴△ACD∽△ABC,∴=,∴AC2=AD·AB,
∴CE·BC=AD·AB;
(3)若AC=3,BC=4,点P在运动的过程中,直线PQ交边AB于点F,当△BQF是等腰三角形时,求线段AP的长.
(3)解:如图,设射线BQ交CD于点W,连接AW,
①如图1,当BF=BQ时,
∵∠ABC=∠ABW,∴点C,W关于AB对称,
∴AC=AW=3,∠AWB=∠ACB=90°,
∵∠PAQ=∠CAB,=,
∴△ACB∽△APQ,∴∠APQ=∠ACB=90°,
∴∠APQ+∠AWQ=180°,∴∠BQF=∠WAP,
∵BF=BQ,∴∠BQF=∠BFQ=∠AFP,
∵∠APD+∠DPF=∠DPF+∠PFD=90°,
∴∠APD=∠AFP,∴∠WAP=∠APW,∴AW=PW=3,
在Rt△ABC中,∵AC=3,BC=4,∴AB=5,
∵AC2=AD·AB,∴AD=,∴DW==,
∴DP=PW-DW=,∴AP==;
②如图2,当FQ=FB时,易证AP=PW,
∴DP=DW-PW=-AP,
在Rt△ADP中,AD2+DP2=AP2,
即()2+(-AP)2=AP2,
解得AP=;
③∵∠BFQ>∠AQP=∠ABQ,∴FQ≠BQ,
综上所述,满足条件的AP的长为或.
谢 谢 观 看
第12课时 相似三角形的应用
第23章 图形的相似
一、选择题
1.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是18m,则旗杆的高度是( C )
A.9m B.11m C.12m D.27m
C
2.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C到旗杆底部D的距离是4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A到小丽头顶的距离是4cm,则旗杆DE的高度为( B )
B
第2题图
A.10m B.12m C.12.4m D.12.32m
二、填空题
3.如图,小明在打网球时,网高0.9m,击球点到球网的水平距离是10m,要使球恰好能打过网,而且落在离网5m的位置上,则球拍击球的高度h应为 2.7 m.
第3题图
2.7
4.如图是斜靠在墙壁上的长梯,梯脚B距离墙1.6m,梯上点D距离墙1.4m,BD的长为0.55m,则梯子的长为 4.4m .
第4题图
4.4m
三、解答题
5.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的这一侧选点A,B,D,使AB⊥AO,DB⊥AB,然后确定DO和AB的交点C,测得AC=120m,CB=60m,BD=50m,请你帮助他们算出峡谷的宽AO.
第5题图
解:∵AB⊥AO,DB⊥AB,∴∠A=∠B=90°,
∵∠ACO=∠BCD,
∴△ACO∽△BCD,
∴=,
∵AC=120m,CB=60m,BD=50m,
∴=,∴AO=100m,
答:峡谷的宽AO是100m.
6.如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.请你利用小明测量的数据算出电线杆AB的高.
第6题图
解:如图,过点C作CG⊥AB于点G,
∴GC=BD=3米,GB=CD=2米,
∵太阳光线是平行光线,
∴∠NFM=∠ACG,
∵∠NMF=∠AGC=90°,
∴△NMF∽△AGC,
∴=,
∴AG==6米,
∴AB=AG+GB=8米,
答:电线杆AB的高为8米.
一、选择题
7.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( B )
第7题图
B
A.4 m B.m C.5m D.m
二、填空题
8.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为15cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座点B,若不考虑其它因素,此时该台灯在桌面可照亮的宽度BD的长为 75 cm.
第8题图
75
三、解答题
9.如图,某同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时尺子的刻度为12cm,已知臂长60cm,求电线杆的高度.
第9题图
解:如图,∵DF∥EC,
∴△ADF∽△AEC,
∴=,
∵GF⊥EC,BC⊥EC,
∴GF∥BC,
∴△AGF∽△ABC,∴=,∴=,
∵DF=0.6m,GF=0.12m,EC=30m,
∴=,∴BC=6m,
答:电线杆的高度为6m.
解答题
10.如图,学校的围墙外有一旗杆AB,甲在操场上C处直立3m高的竹竿CD,乙从C处退到E处恰好看到竹竿顶端D,与旗杆顶端B重合,量得CE=3m,乙的眼睛到地面的距离FE=1.5m,丙在C1处也直立3m高的竹竿C1D1,乙从E处退后6m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旗杆顶端B也重合,测得C1E1=4m,求旗杆AB的高.
第10题图
解:设BO=xm,GO=ym,
∵GD∥OB,
∴△DGF∽△BOF,
∴=,
即=①,
同理可得:△D1HF1∽ △BOF1,
∴=,
即=②,
联立①、②解得,
∴旗杆AB的高为9+1.5=10.5m.
谢 谢 观 看
第13课时 三角形的中位线
第23章 图形的相似
一、选择题
1.已知三角形的周长是16,则它的三条中位线围成的三角形的周长是( C )
A.16 B.12 C.8 D.4
2.如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,已知∠ADE=65°,则∠CFE的度数为( B )
A.60°
B.65°
C.70°
D.75°
第2题图
C
B
二、填空题
3.如图,在△ABC中,AE是BC边上的中线,点G是△ABC的重心,过点G作GF∥AB交BC于点F,那么= .
第3题图
4.如图, ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 3 厘米.
第4题图
3
三、解答题
5.如图,△ABC中,D,E,F分别是AB,AC,BC的中点.
(1)若EF=5cm,则AB= cm,
若BC=9cm,则DE= cm;
解:(1)∵D,E,F分别是AB,AC,BC的中点,
∴AB=2EF=10cm,DE=BC=4.5cm,
故答案为:10,4.5;
第5题图
(2)中线AF与中位线DE有什么特殊的关系?证明你的猜想.
解:(2)互相平分,
证明:如图,连接DF,
∵D,E,F分别是AB,AC,BC的中点,
∴AD=EF=AB,AD∥EF,
∴四边形ADFE为平行四边形,
∴中线AF与中位线DE的关系是互相平分.
第5题图
6.如图,四边形ABCD中,一组对边AB=DC=4,另一组对边AD≠BC,对角线BD与边DC互相垂直,M、N、H分别是AD、BC、BD的中点,且∠ABD=30°.求:
(1)MH的长;
解:(1)∵M、H分别是AD、BD的中点,
∴MH∥AB,MH=AB,
∵AB=4,∴MH=2;
第6题图
(2)MN的长.
解:(2)如图,连接HN,过点H作HQ⊥MN于点Q,
同(1)可知,HN∥DC,HN=DC=2,
∴△MHN是等腰三角形,
∵∠ABD=30°,∠BDC=90°,
∴∠MHD=30°,∠NHD=90°,
∴∠MHN=120°,
∴∠HMQ=∠HNQ=30°,
∵MH=2,∴HQ=MH=1,
∴MQ==,
∵HQ⊥MN,∴MN=2MQ=2.
一、填空题
7.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 11 .
第7题图
11
二、解答题
8.如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点,已知两底差是6,两腰和是12,求△EFG的周长.
第8题图
解:如图,连接AE并延长,交CD于点K,
∵AB∥CD,∴∠BAE=∠DKE,
∵点E是BD的中点,∴BE=DE,
在△AEB和△KED中,,
∴△AEB≌△KED(AAS),
∴DK=AB,AE=EK,
∵EF为△ACK的中位线,
∴EF=CK=(DC-DK)=(DC-AB),
∵EG为△BCD的中位线,∴EG=BC,
又∵FG为△ACD的中位线,∴FG=AD,
∴EG+GF=(AD+BC),
∵两腰和是12,∴AD+BC=12,
∵两底差是6,∴DC-AB=6,
∴EG+GF=6,EF=3,
∴△EFG的周长为EG+GF+EF=9.
解答题
9.已知在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC,过AB、DC的中点E、F作直线,直线EF与直线AD、BC分别相交于点M、N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE、HF,根据三角形中位线定理和平行线的性质,判断∠AMF与∠BNE有何数量关系?(不需证明)
解:(1)∠AMF=∠BNE;
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠BNE有何数量关系?请分别写出猜想,并任选一种情况证明.
解:(2)题图2:∠AMF=∠BNE,
证明:如图1,取AC的中点H,连接HE、HF,
∵F是DC的中点,H是AC的中点,
∴HF∥AD,HF=AD,∴∠AMF=∠HFE,
同理,HE∥CB,HE=CB,∴∠BNE=∠HEF,
∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,
∴∠AMF=∠BNE;
图1
图1
题图3:∠AMF+∠BNE=180°,
证明:如图2,取AC的中点H,连接HE、HF,
∵F是DC的中点,H是AC的中点,
∴HF∥AD,HF=AD,∴∠AMF+∠HFE=180°,
同理,HE∥CB,HE=CB,∴∠BNE=∠HEF,
∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,
∴∠AMF+∠BNE=180°.
谢 谢 观 看
第14课时 位似图形
第23章 图形的相似
一、选择题
1. 在△ABC中,AB=AC,∠A=36°,以点A为位似中心,把△ABC放大到原来的2倍后得△AB'C',则∠B'=( C )
A.36° B.54° C.72° D.144°
C
2.如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形,O为位似中心,OD=OD',则A'B'∶AB=( D )
A.2∶3 B.3∶2 C.1∶2 D.2∶1
第2题图
D
二、填空题
3.如图,已知△ABC与△A'B'C'是一对位似三角形,O为位似中心,若AB∶A'B'=3∶1,且OA'=2,则AA'= 4 .
第3题图
4
4. 如图,以O为位似中心,将五边形ABCDE放大得到五边形A'B'C'D'E',已知OA=10cm,OA'=30cm,如果S五边形A'B'C'D'E'=27cm2,那么S五边形ABCDE= 3cm2 .
第4题图
3cm2
三、解答题
5. 在如图所示的方格纸中,按要求作图.(保留作图痕迹)
第5题图
(2)画出以O为位似中心,将△ABC放大到原来的2倍得到的△A2B2C2.
解:(2)如图所示,△A2B2C2即为所求.
(1)画出与△ABC关于直线l对称的图形△A1B1C1;
解:(1)如图所示,△A1B1C1即为所求;
6.如图,在6×8的网格图中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以点O为位似中心,在网格图中作出△A'B'C',使△A'B'C'和△ABC位似,且位似比为1∶2;
解:(1)如图所示,△A'B'C'即为所求;
第6题图
(2)求四边形AA'C'C的周长.(结果保留根号)
解:(2)根据勾股定理,得:
AC==2,
A'C'==,
∴四边形AA'C'C的周长为1++2+2=3+3.
一、填空题
7.若两个位似图形的对应线段长分别为3cm和5cm,且面积之和为68cm2,则较大图形的面积为 50cm2 .
50cm2
二、解答题
8.如图是由边长为1个单位长度的小正方形组成的网格,
(1)以点O为位似中心,在点O的左侧作△A1B1C1,使得它与△ABC的位似比为1∶2;
解:(1)如图所示,△A1B1C1即为所求;
第8题图
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2,并求出点A旋转的路径的长.
解:(2)如图所示,△A2B2C2即为所求,
∵OA==,
∴点A旋转的路径的长为:
=π.
解答题
9.如图,△ABC中,AB=80cm,高CD=60cm,矩形EFGH中,E、F在AB边上,G在BC边上,H在△ABC内,且EF∶GF=2∶1.
第9题图
解:(1)矩形GFEH的位似图形的长与宽的比为2∶1,设其宽IJ=xcm,则长IK=2xcm,
如图,易知△BIJ∽△BCD,△CIK∽△CBA,
∴=①,=②,
①②两式左右两边分别相加得:+=1,
即+=1,解得:x=24,
∴IJ=24cm,∴==,
作法:先找出点I,使=,然后作IJ⊥AB于点J,作IK∥AB交AC于点K,再过点K作KL⊥AB于点L,连接各顶点,四边形IJLK即为所求;
(1)在△ABC内画出矩形GFEH的位似图形,使其顶点在△ABC的边上;(写出作法)
(2)求所作的矩形的面积.
解:(2)由(1)知,该矩形的长IK=48cm,宽IJ=24cm,
∴S矩形IJLK=24×48=1152cm2.
谢 谢 观 看
第15课时 用坐标确定位置
第23章 图形的相似
一、选择题
1.根据下列表述,能确定位置的是( C )
A.北偏东60°
B.成都市春熙路
C.东经118°,北纬40°
D.奥斯卡影院1号厅3排
C
2.下列关于坐标的说法正确的是( D )
A.(3,4)与(4,3)表示的位置相同
B.(a,b)与(b,a)表示的位置肯定不同
C.坐标(4,4)与(4,4)表示两个不同的位置
D.(3,5)与(5,3)是表示不同位置的两个有序数对
D
3.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置为(2,90°)、B的位置为(4,210°),则C的位置为( C )
第3题图
A.(-2,150°) B.(150°,3)
C.(4,150°) D.(3,150°)
C
二、填空题
4.将某会场座位号“7排4号”记作(7,4),那么“3排5号”记作 (3,5) .
5.如图把QQ“笑脸”图标放在直角坐标系中,已知点A的坐标是(-2,3),点B的坐标是(0,3),则嘴唇点C的坐标是 (-1,1) .
(3,5)
(-1,1)
北偏西25°方向,距离为
300m
第5题图
6.学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对于小亮家的位置是 北偏西25°方向,距离为300m .
三、解答题
7.如图所示的是某市市政府周边的一些建筑,以市政府为坐标原点,建立平面直角坐标系(每个小方格的边长为1).
(1)请写出商会大厦和医院的坐标;
解:(1)由图可得:商会大厦的坐标为(-1,2),
医院的坐标为(3,1);
第7题图
(2)王老师在市政府办完事情后,沿(2,0)→(2,-1)→(2,-3)→(0,-3)→(0,-1)→(-2,-1)的路线逛了一下,然后到汽车站坐车回家,写出他路上经过的地方.
解:(2)他路上经过的地方有大剧院,体育公园,购物广场.
8.在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(-3,1)、(-2,-3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
解:(1)如图,根据A(-3,1),B(-2,-3)画出直角坐标系,描出点C(3,2);
第8题图
(2)若同学们打算从点B处直接赶往点C处,请用方向角和距离描述点C相对于点B的位置.
解:(2)BC=5km,
∴点C在点B的东北方向,与点B相距5 km.
一、选择题
9.在一次中学生野外生存训练活动中,每位队员都配发了一张地图,并接到训练任务,要求36小时之内到达目的地,但是,地图上并未标明目的地的具体位置,仅知道A、B两地的坐标分别为A(-1,2)、B(3,2)且目的地与A、B两地的距离分别为5、3,如图所示,则目的地的具体位置的坐标为( B )
第9题图
B
A.(3,5)
B.(3,5)或(3,-1)
C.(-1,-1)或(3,-1)
D.(3,-1)
10.如图,一个粒子在x轴上及第一象限内运动,第1次从(0,0)运动到(1,0),第2次从(1,0)运动到(2,0),第3次从(2,0)运动到(1,1),它接着按图中箭头所示的方向运动,则它第2023次运动到达的点为( C )
第10题图
A.(55,8) B.(56,7)
C.(58,6) D.(59,5)
C
二、填空题
11.如图,在一座高层的商业大厦中,每层的摊位布局基本相同.若第六层的高档服装销售摊位可表示为(6,2,3),则第六层的手表摊位可表示为 (6,4,5) .
第11题图
(6,4,5)
三、解答题
12.象棋在中国有近三千年的历史,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.
(1)若点A的坐标为(-4,4),点B的坐标为(3,1),写出棋子“帅”“马”和“兵”所在点的坐标;
解:(1)由A(-4,4),B(3,1),可知坐标系如图所示,
则帅(1,0)、马(2,3)、兵(-2,1);
第12题图
(2)若“马”的位置在点A,为了到达点B,请按“马”走的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.
解:(2)如图所示,A(-4,4)→(-2,3)→(0,2)→(2,3)→B(3,1).(答案不唯一)
谢 谢 观 看
第16课时 图形的变换与坐标
第23章 图形的相似
一、选择题
1.点P(-2,1)向上平移2个单位后的点的坐标为( A )
A.(-2,3) B.(0,3)
C.(2,-1) D.(0,1)
2.在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(-2,3),则点N的坐标为( C )
A.(-3,2) B.(2,3)
C.(2,-3) D.(-2,-3)
A
C
3.在平面直角坐标系中,若点P(-3,a)与点Q(b,-4)关于x轴对称,则a+b=( C )
A.-7 B.7 C.1 D.-1
4.在平面直角坐标系中,将点A(1,2)绕点P(-1,1)顺时针旋转90°到点A'处,则点A'的坐标为( B )
A.(-2,3) B.(0,-1)
C.(1,0) D.(-3,0)
C
B
二、填空题
5.点M(2,4)先向左平移3个单位长度,再向上平移2个单位长度得到的点的坐标是 (-1,6) .
(-1,6)
三、解答题
6.△ABC与△A'B'C'在平面直角坐标系中的位置如图所示,△A'B'C'是由△ABC经过平移得到的.
(1)分别写出点A',B',C'的坐标;
解:(1)A'(-3,1),B'(-2,-2),C'(-1,-1);
第6题图
(2)说明△A'B'C'是由△ABC经过怎样的平移得到的;
解:(2)△A'B'C'是由△ABC先向左平移4个单位长度,再向下平移2个单位长度得到的;
(3)若点P(a,b)是△ABC内的一点,平移后△A'B'C'内的对应点为P',写出点P'的坐标.
解:(3)平移后△A'B'C'内的对应点P'的坐标为(a-4,b-2).
7.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点A的坐标为(-3,4).
(1)画出与△ABC关于y轴对称的图形△A1B1C1,并写出点A1的坐标;
解:(1)如图所示,△A1B1C1即为所求,A1(3,4);
第7题图
(2)画出将△ABC绕原点O逆时针旋转90°得到的△A2B2C2,并写出点A2的坐标;
解:(2)如图所示,△A2B2C2即为所求,A2(-4,-3);
(3)求出(2)中点A所经过的路径的长度.
解:(3)点A所经过的路径的长度为:
=π.
一、填空题
8.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点B的对应点B'的横坐标是a,则点B的横坐标是 -(a+3) .
第8题图
-(a+3)
二、解答题
9.如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)画出△A'B'C',并写出点A'、B'、C'的坐标;
解:(1)如图所示,△A'B'C'即为所求,
A'(0,4)、B'(-1,1)、C'(3,1);
第9题图
(2)求出△ABC的面积;
解:(2)S△ABC=×(3+1)×3=6;
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
解:(3)设P(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得×4×|y+2|=6,
解得y=1或-5,
∴点P的坐标为(0,1)或(0,-5).
解答题
10.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(7,1)、B(8,2)、C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形;(要求与△ABC在点P的同一侧)
解:(1)如图所示,△A'B'C'即为所求,
第10题图
(2)求线段BC的对应线段B'C'所在直线的解析式.
解:(2)如图,作BD⊥x轴于点D,B'E⊥x轴于点E,
∴B'E∥BD,==,
∵B(8,2),∴OD=8,BD=2,
∵P(12,0),∴OP=12,∴PD=OP-OD=4,
∵△A'B'C'与△ABC的相似比为3,
∴=3,∴==3,∴B'E=6,PE=12,
∵PO=PE,∴点E与点O重合,∴B'(0,6),同理PC'∶PC=3∶1,
又∵PC=OP-OC=3,∴PC'=9,
∴OC'=OP-PC'=3,∴C'(3,0),
设线段B'C'所在直线的解析式为y=kx+b,
则,解得,
∴线段B'C'所在直线的解析式为y=-2x+6.
谢 谢 观 看
第17课时 复习巩固
第23章 图形的相似
一、选择题
1.课间操时,小华、小军、小刚的位置如图所示,如果小军的位置用(0,-2)表示,小刚的位置用(2,0)表示,那么小华的位置可以表示为( A )
第1题图
A
A.(-2,-3) B.(-3,-2)
C.(-3,-4) D.(-4,-3)
2.将点P(m+2,2m+1)向左平移1个单位长度得到点P',且点P'在y轴上,那么点P'的坐标是( A )
A.(0,-1) B.(0,-2)
C.(0,-3) D.(1,1)
A
3.如图,下列条件中不能判定△ACD∽△ABC的是( B )
第3题图
A.∠ADC=∠ACB B.=
C.∠ACD=∠B D.AC2=AD·AB
B
4.如图,△ABC的两条中线BE、CD交于点O,连接DE,则下列结论不正确的是( B )
第4题图
A.= B.S△DOE∶S△BOC=1∶2
C.= D.△ADE∽△ABC
B
二、填空题
5.若===,则= .
6.如图,小雅同学在利用标杆BE测量建筑物的高度时,测得标杆BE高1.2m,又知AB∶BC=1∶8,则建筑物CD的高是 10.8m .
第6题图
10.8m
三、解答题
7.如图,在边长为9的正△ABC中,BD=3,∠ADE=60°,求AE的长.
第7题图
解:∵∠ADE=60°,
∴∠ADB+∠CDE=120°,
∵△ABC是正三角形,
∴∠B=∠C=60°,
∴∠ADB+∠BAD=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,∴=,
∵BD=3,BC=AB=AC=9,
∴CD=BC-BD=6,∴=,
∴CE=2,∴AE=AC-CE=7.
8.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
解:(1)如图,△A1B1C1即为所求;
第8题图
(2)以M为位似中心,在第一象限中画出将△A1B1C1按照2∶1放大后的位似图形△A2B2C2;
解:(2)如图,△A2B2C2即为所求;
(3)△A2B2C2面积为 .
解:(3)14.
一、选择题
9.如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于E,则BE∶EC=( B )
第9题图
A.1∶2 B.1∶3 C.1∶4 D.2∶3
B
二、填空题
10.如图,在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1,过点M1作M1A1⊥OA于点A1;过点A1作A1M2⊥AB于点M2,过点M2作M2A2⊥OA于点A2;…,以此类推,点M2023的坐标为 (1-,) .
第10题图
(1-,)
三、解答题
11.在正方形ABCD中,对角线AC与BD相交于点O,点E是BC边上的一个动点,连接DE,交AC于点F.
(1)如图1,当=时,求的值;
(1)解:∵=,∴=,
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,∴△CEF∽△ADF,
∴=,∴==,∴==;
(2)如图2,当DE平分∠CDB时,求证:AF=OA;
(2)证明:∵DE平分∠CDB,∴∠ODF=∠CDF,
∵AC、BD是正方形ABCD的对角线,
∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,
又∵∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,
∴∠ADF=∠AFD,∴AD=AF,
在Rt△AOD中,AD==OA,
∴AF=OA;
(3)如图3,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=BG.
(3)证明:∵点E是BC的中点,∴=,
由(1)知==,∴=,
又∵FG⊥BC,CD⊥BC,∴FG∥CD,
∴△EGF∽△ECD,∴==,
在Rt△FGC中,∵∠GCF=45°,∴CG=GF,
又∵CD=BC,∴=,=,
∴CG=BG.
谢 谢 观 看
