第24章 解直角三角形 习题课件(共138张PPT) 2024-2025学年数学华东师大版九年级上册
文档属性
| 名称 | 第24章 解直角三角形 习题课件(共138张PPT) 2024-2025学年数学华东师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 10:33:43 | ||
图片预览







文档简介
(共138张PPT)
第1课时 测量、直角三角形的性质
第24章 解直角三角形
一、选择题
1.在直角三角形中,有一个锐角是另一个锐角的2倍,则这个锐角的度数是( D )
A.30° B.40° C.45° D.60°
2.直角三角形的斜边长为6cm,则斜边上的中线长为( C )
A.2cm B.2.5cm C.3cm D.4cm
D
C
3.如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=1,则AD的长为( B )
第3题图
A.1.5 B.2 C.3 D.4
B
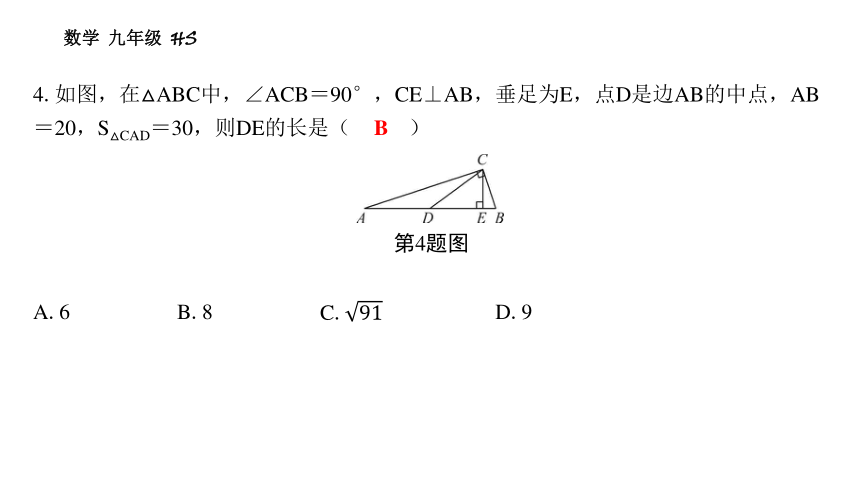
4.如图,在△ABC中,∠ACB=90°,CE⊥AB,垂足为E,点D是边AB的中点,AB=20,S△CAD=30,则DE的长是( B )
第4题图
A.6 B.8 C. D.9
B
二、填空题
5.在Rt△ABC中,∠C=90°,∠A-∠B=60°,那么∠A= 75 °.
6.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,若BC=12cm,AC=9cm,则BD的长是 cm .
第6题图
75
cm
三、解答题
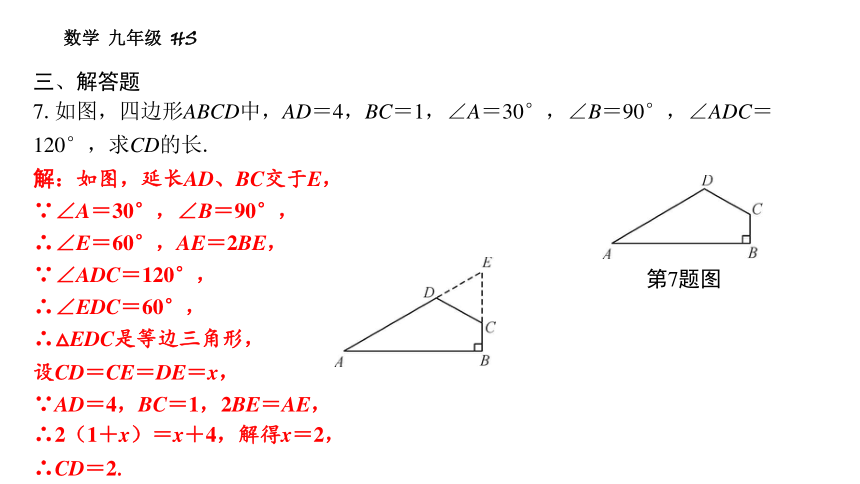
7.如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
第7题图
解:如图,延长AD、BC交于E,
∵∠A=30°,∠B=90°,
∴∠E=60°,AE=2BE,
∵∠ADC=120°,
∴∠EDC=60°,
∴△EDC是等边三角形,
设CD=CE=DE=x,
∵AD=4,BC=1,2BE=AE,
∴2(1+x)=x+4,解得x=2,
∴CD=2.
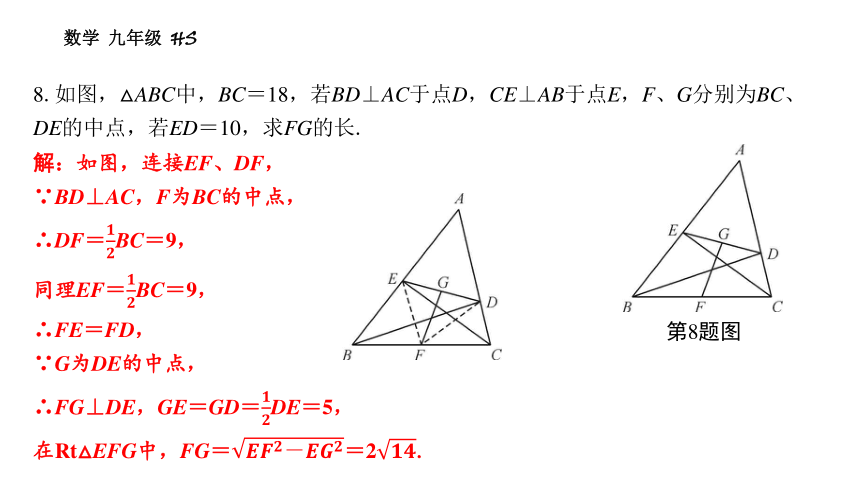
8.如图,△ABC中,BC=18,若BD⊥AC于点D,CE⊥AB于点E,F、G分别为BC、DE的中点,若ED=10,求FG的长.
第8题图
解:如图,连接EF、DF,
∵BD⊥AC,F为BC的中点,
∴DF=BC=9,
同理EF=BC=9,
∴FE=FD,
∵G为DE的中点,
∴FG⊥DE,GE=GD=DE=5,
在Rt△EFG中,FG==2.
一、选择题
9.如图,在Rt△ABC中,∠ACB=90°,点E、F为直角边BC、AC的中点,且AE=3,BF=4,则AB=( C )
第9题图
C
A.2 B.3 C.2 D.5
二、填空题
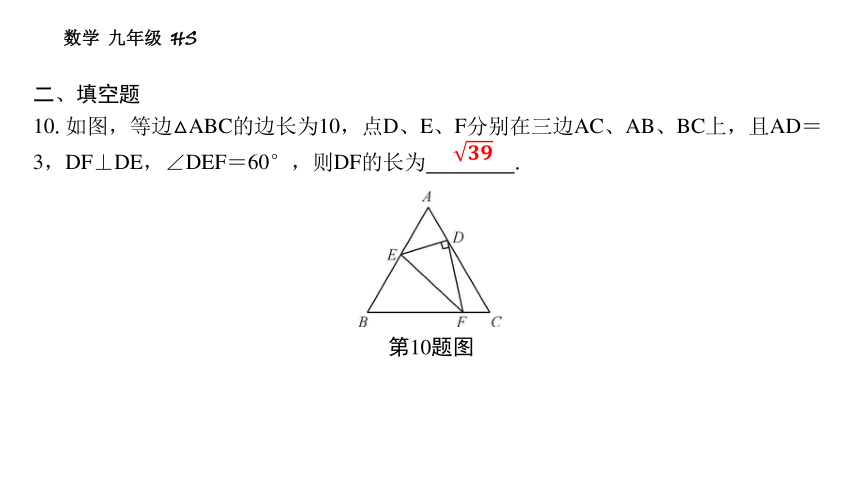
10.如图,等边△ABC的边长为10,点D、E、F分别在三边AC、AB、BC上,且AD=3,DF⊥DE,∠DEF=60°,则DF的长为 .
第10题图
三、解答题
11.如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P,沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上,求小岛A到港口P的距离.
第11题图
解:如图,作AE⊥PB交PB的延长线于E,
由题意得,PB=12×1.5=18海里,
设AE=x海里,∵∠APE=45°,∴PE=AE=x海里,
∵∠ABE=60°,
∴BE=x海里,
∵PE-BE=BP,
∴x-x=18,
解得x=27+9,
则AP=x=(27+9)海里,
答:小岛A到港口P的距离为(27+9)海里.
解答题
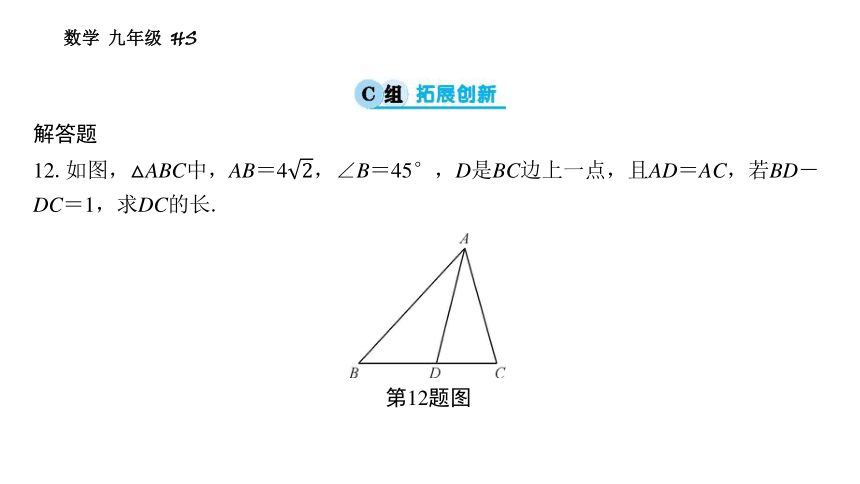
12.如图,△ABC中,AB=4,∠B=45°,D是BC边上一点,且AD=AC,若BD-DC=1,求DC的长.
第12题图
解:如图,过点A作AE⊥BC于点E,
∵AD=AC,AE⊥BC,
∴∠AEB=90°,DE=CE,
∵∠B=45°,
∴∠BAE=45°,
∴AE=BE,
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2=(4)2,
解得BE=4,
∴BD+DC=4,
又∵BD-DC=1,
∴DC=3,
∴DC=2.
谢 谢 观 看
第2课时 锐角三角函数(1)
第24章 解直角三角形
一、选择题
1.(1)在Rt△ABC中,∠C=90°,如果BC=5,AB=13,那么sinA的值为( A )
A. B. C. D.
(2)已知Rt△ABC中,∠C=90°,AC=3,BC=5,那么tanA的值为( C )
A. B. C. D.
(3)在Rt△ABC中,∠C=90°,AB=3BC,则cosA的值为( D )
A. B. C. D.
A
C
D
2.△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( D )
A.sinA= B.cosA=
C.sinA= D.tanA=
3.在Rt△ABC中,∠C=90°,AB=,tanB=2,则AC的长为( B )
A.1 B.2 C. D.2
4.在Rt△ABC中,∠C=90°,∠B=53°,若BC=m,则AB的长为( A )
A. B.m·cos53°
C.m·sin53° D.m·tan53°
D
B
A
二、填空题
5.在Rt△ABC中,∠C=90°,若=,则sinA= .
6.如图,将∠BAC放置在5×5的正方形网格中,若顶点A在格点上,则sin∠BAC的值为 .
第6题图
三、解答题
7.分别求出下列直角三角形中两个锐角的正弦值、 余弦值和正切值.
第7题图
解: (1) 由勾股定理, 得BC==5,
∴sinA==,cosA==,tanA==,
sinB==,cosB==,tanB==;
(2) 由勾股定理, 得AB==,
∴sinA==,cosA==,
tanA==,
sinB==,cosB==,tanB==.
8.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2,求tanB的值.
第8题图
解:如图,过点A作AH⊥BC于点H,
∵S△ABC=×9AH=27cm2,
∴AH=6cm,
∵AB=10cm,
∴BH==8cm,
∴tanB===.
一、填空题
9.如图,在△ABC中,∠A=90°,AB=AC,D为AC边上一点,且AD∶DC=1∶2,则tan∠DBA= .
第9题图
二、解答题
10.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
第10题图
解:在Rt△BCD中,CD=3,BD=5,∠C=90°,
∴BC==4,
又∵AC=AD+CD=8,
在Rt△ABC中,∠C=90°,
∴AB==4,
∴sinA===,
cosA===,
tanA===.
解答题
11.如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象交于第二、四象限内的A、B两点,过点A作AD⊥x轴于点D,AD=4,sin∠AOD=,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
第11题图
解:(1)∵AD⊥x轴,∴∠ADO=90°,
在Rt△AOD中,AD=4,sin∠AOD=,
∴AO==5,
∴根据勾股定理,得OD==3,
∵点A在第二象限,∴A(-3,4),
将A(-3,4)代入y=,得m=-3×4=-12,
∴反比例函数的解析式为y=-,
将B(n,-2)代入y=-,得n=6,
∴B(6,-2),
将A(-3,4),B(6,-2)代入y=kx+b,
得,解得,
∴一次函数的解析式为y=-x+2;
(2)请直接写出满足kx+b>的x的取值范围;
解:(2)由图象知,满足kx+b>的x的取值范围为x<-3或0<x<6;
(3)E是y轴上一点,且△AOE是等腰三角形,求出所有符合条件的点E的坐标.
解:(3)设点E的坐标为(0,a),
∵A(-3,4),O(0,0),
∴OE=|a|,OA=5,AE=,
由△AOE是等腰三角形,则:
①当OA=OE时,|a|=5,∴a=±5,
∴E(0,5)或(0,-5);
②当OA=AE时,5=,
∴a=8或a=0(舍),∴E(0,8);
③当OE=AE时,|a|=,
∴a=,∴E(0,),
综上所述,满足条件的点E的坐标为(0,5)或(0,-5)或(0,8)或(0,).
谢 谢 观 看
第3课时 锐角三角函数(2)
第24章 解直角三角形
一、选择题
1.已知∠A是锐角,tanA=1,那么∠A的度数是( C )
A.15° B.30° C.45° D.60°
2.在Rt△ABC中,∠C=90°,∠A=60°,则sinA+cosB的值为( B )
A. B. C. D.
3.已知α为锐角,且sin(α-10°)=,则α=( A )
A.70° B.60° C.50° D.30°
C
B
A
4.在△ABC中,若|sinA-|+(-cosB)2=0,∠A,∠B都是锐角,则∠C=( C )
A.75° B.90° C.105° D.120°
C
二、填空题
5.在Rt△ABC中,∠C=90°,AB=2,AC=,则∠B的度数为 60° .
6.在△ABC中,sinB=cos(90°-∠C)=,则∠A的度数是 120° .
60°
120°
三、解答题
7.计算:
(1)cos30°+sin45°;
解:原式=×+×
=+1
=.
(2)·tan 30°;
解:原式=×
=××
=.
(3)(sin60°+cos45°)(sin60°-cos45°);
解:原式=sin260°-cos245°
=()2-()2
=-
=.
(4)6tan230°-sin60°-2sin45°;
解:原式=6×()2-×-2×
=2--
=-.
(5);
解:原式=
=-×
=.
(6)tan30°-+tan45°·cos45°.
解:原式=-(-1)+
=-+1+.
8.设β为锐角,且x2+2x+sinβ=0的两根之差为,求β的度数.
解:设方程x2+2x+sinβ=0的两根为x1,x2,
由根与系数的关系知x1+x2=-2,x1x2=sinβ,
由题意知:|x1-x2|=,
∴=-4x1x2=4-4sinβ=2,
解得sinβ=,
∴β=30°.
一、填空题
9.如图(a)是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图(b),再沿BF折叠成图(c),则图(c)中的tan∠DHF的值是 .
第9题图
二、解答题
10.A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道将A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:≈1.414,≈1.732)
第10题图
解:如图,过点C作CD⊥AB于点D,
∵AC=20km,∠CAB=30°,
∴ CD=AC=10km,
AD=AC=10km,
∵∠CBA=45°,
∴BD=CD=10km,BC=CD≈14.14km,
∴AB=AD+BD=10+10≈27.32km,
则AC+BC-AB≈20+14.14-27.32≈6.8km,
答:从A地到B地的路程将缩短约6.8km.
解答题
11.亲爱的同学们,在我们进入高中以后,将会学到三角函数公式:sin(α+β)=sinαcosβ+cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ.
例如:sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°=.
(1)试仿照例题,求出cos75°的准确值;
解:(1)cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin 45°=×-×=;
(2)我们知道tanα=,试求出tan75°的准确值;
解:(2)tan75°===2+;
(3)根据所学知识,请你巧妙地构造一个合适的直角三角形,求出tan75°的准确值(要求分母有理化),和(2)中的结论进行比较.
解:(3)如图,
tan75°=tan∠CBD===+2,
与(2)中的结论一致.
谢 谢 观 看
第4课时 锐角三角函数(3)
第24章 解直角三角形
一、选择题
1.sin240°+cos240°的值为( C )
A.0 B. C.1 D.2
2.如果α是锐角,且sinα=,那么cos(90°-α)的值为( B )
A. B. C. D.
C
B
3.如果锐角α的正弦值为,那么下列结论正确的是( C )
A.α=30° B.α=45°
C.30°<α<45° D.45°<α<60°
C
二、填空题
4.比较大小:(填“>”“<”或“=”)
(1)cos27° > cos63°;
(2)sin44° < cos44°.
5.已知∠A为锐角,且cosA≤,那么∠A度数的取值范围是 60°≤∠A<90° .
6.已知α为锐角,如果sinα+cosα=,那么sinα·cosα= .
>
<
60°≤∠A<90°
三、解答题
7.已知tanα=,α是锐角,求tan(90°-α),sinα,cosα的值.
解:如图,∵tanB=tanα=,
∴设AC=2x,BC=5x,
则AB=x,
∴tan(90°-α)==,
sinα===,
cosα===.
8.根据三角函数规律比较大小.
(1)比较sin46°和cos20°的大小;
解:∵sin46°=cos44°,且44°>20°,
∴cos44°<cos20°,
即sin46°<cos20°.
(2)比较sin20°、cos60°和tan45°的大小;
解:∵sin20°=cos70°,70°>60°,
∴cos70°<cos60°=,
∵tan45°=1,
∴cos70°<cos60°<tan45°,
即sin20°<cos60°<tan45°.
(3)比较sin20°、cos80°和tan45°的大小.
解:∵sin20°=cos70°,80°>70°,tan45°=1,
∴cos80°<cos70°<cos60°<tan45°,
即cos80°<sin 20°<tan45°.
9.计算:sin266°-tan54°tan36°+sin224°+sin230°+cos230°+.
解:原式=sin266°+sin224°-1+1+
=sin266°+cos266°+9
=10.
一、填空题
10.若α是锐角,=1+,则α的度数为 40° .
40°
二、解答题
11.(1)若α为锐角,且sinα+cosα=,求sinα-cosα的值;
解:∵(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+2sinαcosα,sinα+cosα=,
∴1+2sinαcosα=,
∴2sinαcosα=,
∴(sinα-cosα)2=sin2α+cos2α-2sinαcosα=1-=,
∵α为锐角,∴sinα-cosα=±.
(2)已知sina,cosa是关于x的方程8x2+6mx+2m+1=0的两根,求+的值.
解:由根与系数的关系,
得sina+cosa=-,sina·cosa=,
∵(sina+cosa)2=1+2sina·cosa,
∴=1+2×,解得m=2或-,
∵Δ=36m2-4×8×(2m+1)
=4(9m2-16m-8),
当m=2时,Δ=-16<0,故舍去,
当m=-时,Δ=>0,
∴m=-,
∴+==-=-.
解答题
12.如图,海中有一个小岛A,该岛的四周10海里的范围内有暗礁.有一货轮在海面上由西向东航行,到达B处时,该货轮位于小岛南偏西60°的方向上,再往东行驶20海里后到达小岛的南偏西30°的方向上的C处,如果货轮继续向东航行,是否会有触礁的危险?请通过计算说明.
第12题图
解:如图,过点A作AD⊥BC交BC延长线于点D,
由题意,得∠BAD=60°,∠CAD=30°,
∴∠BAC=∠BAD-∠CAD=30°,
又∵∠B=90°-∠BAD=90°-60°=30°,
∴∠B=∠BAC,∴AC=BC=20海里,
在Rt△ACD中,
AD=AC·cos∠CAD=10海里,
由题意知,以海岛A为圆心,10海里为半径的范围内有暗礁,
∵AD=10海里>10海里,
∴如果货轮继续向东航行,没有触礁的危险.
谢 谢 观 看
第5课时 专题锐角三角函数
第24章 解直角三角形
解答题
1.如图,在Rt△ABC中,∠C=90°,AB=10,tanA=,求BC的长和sinB的值.
第1题图
解:∵tanA==,
∴AC=2BC,
在Rt△ABC中,
AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sinB===.
2.如图,在△ABC中,∠B=30°,tanC=,AD⊥BC于点D.若AB=8,求BC的长.
第2题图
解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ADB中,
∠B=30°,AB=8,
∴AD=4,BD=4,
在Rt△ADC中,tanC=,AD=4,
∴CD==3,
∴BC=BD+CD=4+3.
3.如图,在Rt△BCD中,∠BDC=30°,延长CD到点A,连接AB,∠A=15°,求tan15°的值.(结果保留根号)
第3题图
解:∵∠A=15°,∠BDC=30°,
∴∠ABD=15°,
∴AD=BD,
设BC=x,
在Rt△BDC中,∵∠BDC=30°,∴BD=2x,
∴DC==x,
∴AD=BD=2x,AC=AD+DC=(2+)x,
在Rt△ABC中,
tan15°===2-.
4.如图,在△ABC中,BC=AC,∠BCA=135°,求tanA的值.
第4题图
解:如图,过点B作BD⊥AC交AC的延长线于点D,
∵∠BCA=135°,∴∠BCD=45°,
∴BD=CD=BC=AC,
∴AD=AC+CD=2AC,
∴tanA==.
5.在Rt△ABC中,∠C=90°,斜边c=5,两直角边a、b是关于x的一元二次方程x2-mx+2m-2=0的两个根,求Rt△ABC中较大锐角的三个三角函数值.
解:由题意得:a+b=m,ab=2m-2,且a2+b2=c2,
∴-2ab=c2,
即m2-2=25,
解得m1=7,m2=-3,
当m=-3时,ab=-8(舍去),∴m=7,
∴,解得:或,
故Rt△ABC中较大锐角为边长为4的边所对的角,设为α,则sinα=,cosα=,tanα=.
6.如图,在△ADC中,∠A=30°,∠ACD=90°,B在AC上,∠DBC=45°,E在BC的延长线上,且AB=2,CE=3,过E作EF⊥AE,交BD的延长线于F,求EF的长.
第6题图
解:设BC=x,
∵∠DBC=45°,∠ACD=90°,EF⊥AE,
∴EF=BE=3+x,BC=DC=x,
∴AC=2+x,
∵∠A=30°,tanA=,
∴2+x=x,∴x=+1,
∴EF=+4.
7.如图,在△ABC中,∠C=90°,AB=10,sinB=,点D为边BC的中点.
(1)求BC的长;
解:(1)∵∠C=90°,sinB==,AB=10,
∴AC=6,∴由勾股定理可知:BC=8;
第7题图
(2)求∠BAD的正切值.
解:(2)如图,过点D作DE⊥AB,垂足为E,
∵∠C=∠BED=90°,∠B=∠B,
∴△BED∽△BCA,
∴==,
即==,
∴BE=,ED=,
∴AE=AB-BE=10-=,
∴tan∠BAD==.
8.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠DCB=.
(1)求cosB的值;
解:(1)如图,过点A作AE⊥BC于点E,
∵AB=AC=5,
∴BE=CE=BC=×8=4,
在Rt△ABE中,cosB==;
第8题图
(2)求△BCD的面积.
解:(2)如图,过点D作DF⊥BC于点F,
在Rt△CDF中,tan∠DCF==,
设DF=3x,则CF=5x,
在Rt△ABE中,AE==3,
∴tanB==,
在Rt△BDF中,tanB==,
∴BF=4x,
∴BC=BF+CF=4x+5x=9x,
即9x=8,解得x=,
∴DF=3x=,
∴S△BCD=DF·BC=××8=.
谢 谢 观 看
第6课时 解直角三角形(1)
第24章 解直角三角形
一、选择题
1.在Rt△ABC中,∠C=90°,若BC=1,AB=,则tanA的值为( C )
A. B.
C. D.2
2.在Rt△ABC中,∠C=90°,若a=6,∠B=30°,则c和tanA的值分别为( C )
A.12, B.12,
C.4, D.2,
C
C
3.在△ABC中,∠C=90°,下列结论正确的是( D )
A.AC=BC·tanA B.AB=AC·cosA
C.AC=AB·sinA D.AC=BC·tanB
D
二、填空题
4.在△ABC中,∠C=90°,BC=4,sinA=,则AB= 12 .
5.等腰三角形底边与底边上的高的比是2∶,则顶角为 60° .
12
60°
三、解答题
6.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近.为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从船队首(点O)尾(点A)出发前去拦截,4分钟后同时到达点B将可疑快艇驱离.已知OA=20海里,甲直升机每小时飞行180海里,航向为北偏东25°,乙直升机的航向为北偏西65°,求乙直升机的飞行速度.
第6题图
解:由题意得:∠B=25°+65°=90°,
∵OA=20海里,OB=180×=12海里,
∴AB===16海里,
∴16÷=240海里/小时,
答:乙直升机的飞行速度为每小时飞行240海里.
7.如图,有一轮船在A处测得南偏东30°方向上有一小岛F,轮船沿正南方向航行至B处,测得小岛F在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛F在正东方向上,求A,B之间的距离.(结果保留根号)
第7题图
解:在Rt△BCF中,∠CBF=45°,
∴CF=BC=10海里,
在Rt△ACF中,∠CAF=30°,
AC==10海里,
∴AB=AC-BC=10(-1)海里,
答:A,B之间的距离为10(-1)海里.
8.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tanB=.
(1)求AD的长;
解:(1)在Rt△ABC中,tanB==,
∴AC=3x,BC=4x,
∵AC2+BC2=AB2,
∴(3x)2+(4x)2=52,
解得x=1或-1(舍去),
∴AC=3,BC=4,
∵BD=1,∴CD=3,
∴AD==3;
第8题图
(2)求sinα的值.
解:(2)如图,过点D作DE⊥AB于点E,
∵tanB=,
∴设DE=3y,BE=4y,
∵BE2+DE2=BD2,
∴(3y)2+(4y)2=12,
解得y=或-(舍去),
∴DE=,∴sinα==.
一、填空题
9.如图,在Rt△ABC中,∠C=90°,点D是AB的中点,ED⊥AB交AC于点E.设∠A=α,且tanα=,则tan2α= .
第9题图
二、解答题
10.如图,一艘游艇在离开码头A处后,沿南偏西60°方向行驶到达B处,此时从B处发现灯塔C在游轮的东北方向,已知灯塔C在码头A的正西方向200米处,求此时游轮与灯塔C的距离.(精确到1米,参考数据:≈1.414,≈1.732,≈2.449)
第10题图
解:如图,过B作BD⊥AC交AC的延长线于D,
在Rt△BCD中,∠D=90°,∠DBC=45°,
∴∠DCB=∠DBC=45°,BD=CD,
在Rt△ABD中,∠DAB=30°,
∴AD=BD,
∵AC=200米,
∴BD-BD=200,
∴BD==100(+1)米,
∴BC=BD=100(+1)×≈386米,
答:此时游轮与灯塔C的距离约为386米.
解答题
11.如图,一艘船由A港沿北偏东65°方向航行90km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
第11题图
解:由题意得,∠CAB=65°-20°=45°,∠C=40°+20°=60°,AB=90km,
如图,过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∠EAB=45°,
∴AE=BE=AB=90km,
在Rt△CBE中,∠C=60°,
∴CE=BE=30km,
∴AC=AE+CE=(90+30)km,
∴A,C两港之间的距离为(90+30)km.
谢 谢 观 看
第7课时 解直角三角形(2)
第24章 解直角三角形
一、选择题
1.如图,某地修建高速公路,要从B地向C地修一条隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( A )
第1题图
A
A.100m B.50m
C.50m D.m
2.如图,在楼顶点A处观察旗杆CD测得旗杆顶部C的仰角为30°,旗杆底部D的俯角为45°.已知楼高AB=9m,则旗杆CD的高度为( B )
第2题图
A.(9+)m B.(9+3)m
C.9m D.12m
B
二、填空题
3.如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度约为 15.3 米.(结果保留一位小数,参考数据:sin54°≈0.8090,cos54°≈0.5878,tan54°≈1.3764)
第3题图
15.3
三、解答题
4.我市某建筑工地,欲拆除该工地的一危房AB(如图),准备对该危房实施定向爆破.已知距危房AB水平距离60米处有一居民住宅楼CD,该居民住宅楼CD高15米,在该住宅楼顶C处测得此危房屋顶A的仰角为30°,请你通过计算说明在实施定向爆破危房AB时,该居民住宅楼CD有无危险?(在地面上以点B为圆心,AB长为半径的圆形区域为危险区域,参考数据:≈1.414,≈1.732)
第4题图
解:在Rt△AEC中,∠ACE=30°,CE=BD=60米,
∴AE=CE·tan∠ACE≈34.64米,
又∵BE=CD=15米,
∴AB=AE+BE≈49.64米,
∵60>49.64,即BD>AB,
∴在实施定向爆破危房AB时,该居民住宅楼CD没有危险.
5.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者,在消防车上点A处测得点B和点C的仰角分别为45°和65°,点A距地面2.5米,点B距地面10.5米,为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数,参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,≈1.4)
第5题图
解:如图,作AH⊥CN于点H,
在Rt△ABH中,∠BAH=45°,
∴AH=BH=10.5-2.5=8米,
在Rt△AHC中,∠CAH=65°,
∴CH=AH·tan65°≈17米,
∴BC=CH-BH=17-8=9米,
答:云梯需要继续上升的高度BC约为9米.
解答题
6.如图,学校教学楼上悬挂一块长为3m的标语牌CD.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离,测角仪支架高AE=BF=1.2m,小明在E处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由.(图中点A,B,C,D,E,F,H在同一平面内,精确到0.1m,参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
第6题图
解:能.
如图,延长EF交CH于点N,
则∠CNF=90°,
∵∠CFN=45°,∴CN=NF,
设DN=xm,
则NF=CN=(x+3)m,
∴EN=5+(x+3)=(x+8)m,
在Rt△DEN中,DN=EN·tan∠DEN,
即x=(x+8)·tan31°,解得x≈12.0,
则DH=DN+NH≈12.0+1.2=13.2m,
答:点D到地面的距离DH的长约为13.2m.
解答题
7.如图,码头A、B分别在海岛O的北偏东45°和北偏东60°方向上,仓库C在海岛O的北偏东75°方向上,码头A、B均在仓库C的正西方向,码头B和仓库C的距离BC=50km,现将一批物资从仓库C用汽车运送到A、B两个码头中的一处,再用货船运送到海岛O,若汽车的行驶速度为50km/h,货船航行的速度为25km/h,问这批物资在哪个码头装船,最早运抵海岛O?(两个码头物资装船所用的时间相同,参考数据:≈1.4,≈1.7)
第7题图
解:如图,延长CA交OM于K,
由题意得:∠COK=75°,∠BOK=60°,∠AOK=45°,∠CKO=90°,
∴∠KCO=15°,∠KBO=30°,OK=KA,
∵∠KBO=∠C+∠BOC,
∴∠C=∠BOC=15°,
∴OB=BC=50km,
在Rt△OBK中,OK=OB=25km,
KB=OK=25≈42.5km,
在Rt△AOK中,AK=25km,OA=25≈35km,
∴AB=KB-AK≈17.5km,∴AC≈67.5km,
∴在码头A装船运抵海岛O的用时为:
+=2.75h,
在码头B装船船运抵海岛O的用时为:
+=3h,
∵2.75<3,
∴这批物资在码头A装船,最早运抵海岛O.
谢 谢 观 看
第8课时 解直角三角形(3)
第24章 解直角三角形
一、选择题
1.如图,某停车场入口的栏杆,从水平位置AB绕点O旋转到A'B'的位置,已知AO=4米,若栏杆的旋转角∠AOA'=50°,则栏杆A端升高的高度是( B )
第1题图
B
A.米 B.4sin50°米
C.米 D.4cos50°米
2.如图,要测量小河两岸相对的两点P、A之间的距离,可以在小河边PA的垂线PB上取一点C.测得PC=80米,∠PCA=32°,则PA的长为( B )
第2题图
A.80sin32°米 B.80tan32°米
C.米 D.米
B
3.河堤横断面如图所示,AB=10米,tan∠BAC=,则AC的长为( A )
第3题图
A.5米 B.10米 C.15米 D.10米
A
4.如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒,若∠BAC=α,则此车的速度为( A )
第4题图
A.5tanα米/秒 B.80tanα米/秒
C.米/秒 D.米/秒
A
二、填空题
5.(1)小明沿着坡度i=1∶2.5的斜坡前行了29米,那么他上升的高度是 2 米;
(2)有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1∶2.5,那么该斜坡的水平距离AC的长为 75 m.
2
75
6.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成角为32°,缆车速度为每分钟50米,从山脚下A处到达山顶B处缆车需要16分钟,则山的高度BC约为 424 米.(精确到1米,参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249)
第6题图
424
三、解答题
7.如图,扶梯AB的坡比为1∶2,滑梯CD的坡比为1∶.若AE=40m,BC=30m,某人从扶梯上去,经过顶部BC,再沿滑梯滑下,求此人经过的路径长.(结果精确到0.1m,参考数据:≈1.41,≈1.73,≈2.24)
第7题图
解:∵BE∶AE=1∶2,AE=40m,∴BE=20m,
∴AB==20m,
∵CF∶DF=1∶,CF=BE=20m,
∴FD=CF=20m,
∴CD==40m,
∴经过的路径长为AB+BC+CD=20+30+40=70+20≈114.8m,
答:此人经过的路径长约为114.8m.
8.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面示意图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=AC=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长.(结果保留根号)
第8题图
解:如图,延长BA交FD的延长线于点G,过点A作AH⊥DG于点H,
由题意知,AB=300cm,BE=AC=50cm,AH=50cm,∠AGH=30°,
∴在Rt△AGH中,AG=2AH=100cm,
∴CG=AC+AG=150cm,
则CD=CG=75cm,
∵EG=AB-BE+AG=300-50+100=350cm,
∴在Rt△EFG中,
EF=EG·tan∠EGF=cm,
∴支撑角钢CD的长为75cm,EF的长为cm.
解答题
9.如图,在岷江的右岸边有一高楼AB,左岸边有一坡度i=1∶2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行走20m到达D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.(结果保留根号)
第9题图
解:在Rt△DEC中,i==,
∵DE2+EC2=CD2,CD=20m,
∴DE2+(2DE)2=(20)2,
∴DE=20m,∴EC=40m,
如图,作DG⊥AB于点G,作CH⊥DG于点H,
则四边形DEBG、四边形DECH、四边形BCHG都是矩形,
∵∠ACB=45°,AB⊥BC,∴AB=BC,
设AB=BC=xm,
则AG=(x-20)m,DG=(x+40)m,
在Rt△ADG中,=tan∠ADG,∠ADG=30°,
∴=,解得:x=50+30,
答:楼AB的高度为(50+30)m.
谢 谢 观 看
第9课时 专题解直角三角形的应用
第24章 解直角三角形
解答题
1.2023年12月2日是第十二个“全国交通安全日”,主题为“文明守法平安回家”.如图,某观测点设在距高速公路(直线l)100m的P处,一辆轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3s,并测得∠AOP=90°,∠APO=60°,∠BPO=45°,试判断此车是否超过了25m/s的限制速度?(≈1.732)
第1题图
解:由题意得PO=100m,
∵∠PBO=45°,∴BO=PO=100m,
∵∠APO=60°,∴AO=OPtan60°=100m,
∴AB=AO-BO=(100-100)m,
∴此车的速度为≈24.4m/s,
∵24.4m/s<25m/s,
∴此车速度没有超过25m/s的限制速度.
2.商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,扶梯AB的坡度i为1∶,改造后的斜坡式自动扶梯的坡角∠ACB为15°.
(1)求AD的长度;
解:(1)由题意得tan∠ABD=,∴∠ABD=30°,
∴在Rt△ADB中,AD=AB=5m;
第2题图
(2)求改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
解:(2)在Rt△ACD中,sin∠ACD=,
∴AC=≈≈19.2m,
答:改造后的自动扶梯AC的长约为19.2m.
3.如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要从B地绕行.已知B地位于A地的北偏东67°方向,距离A地520km,C地位于B地的南偏东30°方向,若打通穿山隧道,建成A、C两地直达高铁,求A地到C地之间直线高铁线路的长.(结果保留整数,参考数据:sin67°≈,cos67°≈,tan67°≈,≈1.73)
第3题图
解:如图,过点B作BD⊥AC于点D,
在Rt△ABD中,∵∠ABD=67°,AB=520km,
∴AD=ABsin67°≈480km,
BD=ABcos67°≈200km,
∵∠CBD=30°,∴CD=BDtan30°≈115.3km,
∴AC=AD+CD≈480+115.3≈595km,
∴A地到C地之间直线高铁线路的长约是595km.
4.如图1是一个手机支架,图2是其侧面示意图,AB、BC可分别绕点A、B转动,测量知AB=10cm,BC=8cm.当AB,BC转动到∠BAE=70°,∠ABC=65°时,求点C到直线AE的距离.(精确到0.1cm,参考数据:sin70°≈0.94,cos70°≈0.34,≈1.41)
第4题图
解:如图,过点B作BM⊥AE于点M,过点C作CN⊥AE于点N,CD⊥BM于点D,
∴四边形MNCD是矩形,∴DM=CN,
在Rt△ABM中,∠BAE=70°,AB=10cm,
∴∠ABM=20°,BM=ABsin70°≈9.4cm,
∵∠ABC=65°,∴∠CBD=∠ABC-∠ABM=45°,
∴BD=BCcos45°≈5.64cm,
∴CN=DM=BM-BD≈3.8cm,
∴点C到AE的距离约为3.8cm.
5.如图,某建筑物楼顶挂有广告牌BC,小华从点A处沿坡度i=1∶的斜坡步行30米到达点P处,测得广告牌底部C的仰角为45°,广告牌顶部B的仰角为53°,小华的身高忽略不计,已知广告牌BC=12米.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
(1)求点P处距离水平地面的高度;
第5题图
解:(1)如图,过点P作PE⊥AO于点E,
∵坡度i=1∶,
∴tan∠PAE==,∴∠PAE=30°,
∴PE=AP=15米,
即点P处距离水平地面的高度为15米;
(2)求建筑物OC的高度.
解:(2)如图,过点P作PF⊥BO于点F,
∵∠CPF=45°,∠BPF=53°,
∴CF=PF,BF=PF·tan53°≈1.3PF,
∵BC=BF-CF=12米,
∴1.3PF-PF=12,∴PF=CF=40米,
∴OC=CF+OF=CF+PE=55米,
即建筑物OC的高度约为55米.
解答题
6.如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到点D处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,无人机的高度为(30+15)米.(结果保留根号,参考数据:tan75°=2+,tan15°=2-)
(1)求小区楼房BC的高度;
第6题图
解:(1)如图,过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,则四边形BCFE是矩形,
由题意得:AB=45米,DE=(30+15)米,∠DAE=75°,∠DCF=∠FDC=45°,∴CF=DF=BE,
在Rt△ADE中,tan∠DAE==2+,
∴AE==15米,∴BE=DF=AB-AE=30米,
∴EF=DE-DF=15米,
答:小区楼房BC的高度为15米;
(2)若无人机以5米/秒的速度继续沿平行于AB的路线向右匀速飞行.问:经过多少秒,无人机刚好离开操控者的视线?
解:(2)如图,作DG∥AB,交AC的延长线于点G,作GH⊥AB于点H,
∵BC∥GH,∴=,
∴=,∴AH=(30+45)米,
∴DG=EH=AH-AE=(30+30)米,
(30+30)÷5=(6+6)秒,
答:经过(6+6)秒,无人机刚好离开操控者的视线.
解答题
7.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠得到△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
由折叠得,∠BFE=∠C=90°,
∴∠AFB+∠DFE=∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,∴△ABF∽△DFE;
第7题图
(2)若sin∠DFE=,求tan∠EBC的值;
(2)解:在Rt△DEF中,sin∠DFE==,
∴设DE=a,EF=3a,则DF=2a,
由折叠得,∠EBC=∠EBF,CE=EF=3a,
∴AB=CD=DE+CE=4a,
由(1)得:△ABF∽△DFE,∴==,
∴tan∠EBC=tan∠EBF==;
(3)若AF=5cm,BF=10cm,动点M从点B出发,在BF上以每秒2cm的速度向点F匀速运动,同时动点N从点A出发,在AB上以每秒cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN,当△ABF与△BMN相似时,求t的值.
(3)解:∵AF=5cm,BF=10cm,∴AB=5cm,
由题意得,BM=2tcm,BN=(5-t)cm,
①当△NBM∽△ABF时,=,
即=,解得t=;
②当△MBN∽△ABF时,=,
即=,解得t=,
综上所述,t的值为或.
谢 谢 观 看
第10课时 复习巩固
第24章 解直角三角形
一、选择题
1.在△ABC中,∠C=90°,BC=3,tanA=,则边AB的长是( D )
A. B.3 C.4 D.5
2.已知α为锐角,且cos(α-20°)=,那么α的度数为( C )
A.70° B.60° C.50° D.30°
D
C
3.下列各式中,不成立的是( D )
A.sin230°+cos230°=1
B.sin15°=cos75°
C.tan30°·tan60°=1
D.cos60°=2sin30°
4.若α为锐角,cos(α+60°)=0.4,则( A )
A.0°<α<30° B.30°<α<45°
C.45°<α<60° D.60°<α<90°
D
A
二、填空题
5.已知CD是Rt△ABC的斜边AB上的中线,若∠A=35°,则∠BCD= 55° .
6.如图,△ABC中,∠ACB=90°,∠A=30°,AB=4,若CD是高,则BD= 1 .
第6题图
55°
1
7.一山坡的坡度i=1∶3,小刚从山坡脚下点P处上坡走了50米到达点N处,那么他上升的高度是 50 米.
50
三、解答题
8.计算:3tan30°-+cos45°+.
解:原式=3×-2+×+
=-2+2+-1
=2-1.
9.在全校的科技制作大赛中,王浩同学用木板制作了一个带有卡槽的三角形手机架.如图所示,卡槽的宽度DF与内△ABC的AB边长相等.已知AC=20cm,BC=18cm,∠ACB=50°,一个手机的最长边为17cm,王浩同学能否将此手机立放入卡槽DF内?请说明理由.(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
第9题图
解:王浩同学能将手机放入卡槽DF内,理由如下:
如图,作AD⊥BC于点D,
∵∠C=50°,AC=20cm,
∴AD=AC·sin50°≈20×0.8=16cm,
CD=AC·cos50°≈20×0.6=12cm,
∴DB=BC-CD=18-12=6cm,
∴AB===cm,
∴DF=AB=cm,
∵17=<,
∴王浩同学能将手机放入卡槽DF内.
一、选择题
10.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是边AB的中点,AB=10,DE=4,则S△AEC=( B )
A.8
B.7.5
C.7
D.6
第10题图
B
11.规定:对任意角x,y,都有sin2x+cos2x=1,sin(-x)=-sinx,cos(-x)=cosx,cos(x+y)=cosxcosy-sinxsiny,现给出下列等式:①sin(-60°)=-;②cos15°=;③cos2x=1-2sin2x;④cos(x-y)=cosxcosy+sinxsiny;⑤cosxcosy=[cos(x+y)+cos(x-y)],其中等式成立的有( C )
A.2个 B.3个 C.4个 D.5个
C
二、解答题
12.某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到点C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命迹象所在点C处的深度.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
第12题图
解:如图,过点C作CD⊥AB,交AB的延长线于点D,
设CD=x米,
在Rt△ACD中,∠CAD=30°,
∴AD=CD=x米,
在Rt△BCD中,∠CBD=45°,
∴BD=CD=x米,由题意得x-x=6,
解得:x=3(+1)≈8.2,
答:生命迹象所在点C的深度为8.2米.
解答题
13.如图,港口B位于港口A的南偏西45°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的南偏东45°方向的D处,它沿正北方向航行18.5km到达E处,此时测得灯塔C在E处的南偏西70°方向上,求E处距离港口A有多远?(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
第13题图
解:如图,过点B作BM⊥AD,垂足为点M,过点C作CN⊥AD,垂足为点N,
设CN=x km,
在Rt△ACN中,∠A=45°,
∴AN===xkm,
在Rt△ECN中,∠CEN=70°,
∴EN==km,
∵CN⊥AD,BM⊥AD,
∴CN∥BM,
∴==,
又∵C为AB的中点,
∴AB=2AC,AC=BC,
∴BM=2CN=2xkm,AN=MN=xkm,
由题可知,∠MDB=45°,
在Rt△BMD中,∠MDB=45°,
∴DM===2xkm,
∵DE-DM-EN=MN,
∴18.5-2x-=x,
∴x=≈5.5,
∴AE=AN-EN≈5.5-≈3.5km,
答:E处距离港口A约3.5km.
谢 谢 观 看
第1课时 测量、直角三角形的性质
第24章 解直角三角形
一、选择题
1.在直角三角形中,有一个锐角是另一个锐角的2倍,则这个锐角的度数是( D )
A.30° B.40° C.45° D.60°
2.直角三角形的斜边长为6cm,则斜边上的中线长为( C )
A.2cm B.2.5cm C.3cm D.4cm
D
C
3.如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=1,则AD的长为( B )
第3题图
A.1.5 B.2 C.3 D.4
B
4.如图,在△ABC中,∠ACB=90°,CE⊥AB,垂足为E,点D是边AB的中点,AB=20,S△CAD=30,则DE的长是( B )
第4题图
A.6 B.8 C. D.9
B
二、填空题
5.在Rt△ABC中,∠C=90°,∠A-∠B=60°,那么∠A= 75 °.
6.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,若BC=12cm,AC=9cm,则BD的长是 cm .
第6题图
75
cm
三、解答题
7.如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
第7题图
解:如图,延长AD、BC交于E,
∵∠A=30°,∠B=90°,
∴∠E=60°,AE=2BE,
∵∠ADC=120°,
∴∠EDC=60°,
∴△EDC是等边三角形,
设CD=CE=DE=x,
∵AD=4,BC=1,2BE=AE,
∴2(1+x)=x+4,解得x=2,
∴CD=2.
8.如图,△ABC中,BC=18,若BD⊥AC于点D,CE⊥AB于点E,F、G分别为BC、DE的中点,若ED=10,求FG的长.
第8题图
解:如图,连接EF、DF,
∵BD⊥AC,F为BC的中点,
∴DF=BC=9,
同理EF=BC=9,
∴FE=FD,
∵G为DE的中点,
∴FG⊥DE,GE=GD=DE=5,
在Rt△EFG中,FG==2.
一、选择题
9.如图,在Rt△ABC中,∠ACB=90°,点E、F为直角边BC、AC的中点,且AE=3,BF=4,则AB=( C )
第9题图
C
A.2 B.3 C.2 D.5
二、填空题
10.如图,等边△ABC的边长为10,点D、E、F分别在三边AC、AB、BC上,且AD=3,DF⊥DE,∠DEF=60°,则DF的长为 .
第10题图
三、解答题
11.如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P,沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上,求小岛A到港口P的距离.
第11题图
解:如图,作AE⊥PB交PB的延长线于E,
由题意得,PB=12×1.5=18海里,
设AE=x海里,∵∠APE=45°,∴PE=AE=x海里,
∵∠ABE=60°,
∴BE=x海里,
∵PE-BE=BP,
∴x-x=18,
解得x=27+9,
则AP=x=(27+9)海里,
答:小岛A到港口P的距离为(27+9)海里.
解答题
12.如图,△ABC中,AB=4,∠B=45°,D是BC边上一点,且AD=AC,若BD-DC=1,求DC的长.
第12题图
解:如图,过点A作AE⊥BC于点E,
∵AD=AC,AE⊥BC,
∴∠AEB=90°,DE=CE,
∵∠B=45°,
∴∠BAE=45°,
∴AE=BE,
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2=(4)2,
解得BE=4,
∴BD+DC=4,
又∵BD-DC=1,
∴DC=3,
∴DC=2.
谢 谢 观 看
第2课时 锐角三角函数(1)
第24章 解直角三角形
一、选择题
1.(1)在Rt△ABC中,∠C=90°,如果BC=5,AB=13,那么sinA的值为( A )
A. B. C. D.
(2)已知Rt△ABC中,∠C=90°,AC=3,BC=5,那么tanA的值为( C )
A. B. C. D.
(3)在Rt△ABC中,∠C=90°,AB=3BC,则cosA的值为( D )
A. B. C. D.
A
C
D
2.△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( D )
A.sinA= B.cosA=
C.sinA= D.tanA=
3.在Rt△ABC中,∠C=90°,AB=,tanB=2,则AC的长为( B )
A.1 B.2 C. D.2
4.在Rt△ABC中,∠C=90°,∠B=53°,若BC=m,则AB的长为( A )
A. B.m·cos53°
C.m·sin53° D.m·tan53°
D
B
A
二、填空题
5.在Rt△ABC中,∠C=90°,若=,则sinA= .
6.如图,将∠BAC放置在5×5的正方形网格中,若顶点A在格点上,则sin∠BAC的值为 .
第6题图
三、解答题
7.分别求出下列直角三角形中两个锐角的正弦值、 余弦值和正切值.
第7题图
解: (1) 由勾股定理, 得BC==5,
∴sinA==,cosA==,tanA==,
sinB==,cosB==,tanB==;
(2) 由勾股定理, 得AB==,
∴sinA==,cosA==,
tanA==,
sinB==,cosB==,tanB==.
8.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2,求tanB的值.
第8题图
解:如图,过点A作AH⊥BC于点H,
∵S△ABC=×9AH=27cm2,
∴AH=6cm,
∵AB=10cm,
∴BH==8cm,
∴tanB===.
一、填空题
9.如图,在△ABC中,∠A=90°,AB=AC,D为AC边上一点,且AD∶DC=1∶2,则tan∠DBA= .
第9题图
二、解答题
10.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
第10题图
解:在Rt△BCD中,CD=3,BD=5,∠C=90°,
∴BC==4,
又∵AC=AD+CD=8,
在Rt△ABC中,∠C=90°,
∴AB==4,
∴sinA===,
cosA===,
tanA===.
解答题
11.如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象交于第二、四象限内的A、B两点,过点A作AD⊥x轴于点D,AD=4,sin∠AOD=,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
第11题图
解:(1)∵AD⊥x轴,∴∠ADO=90°,
在Rt△AOD中,AD=4,sin∠AOD=,
∴AO==5,
∴根据勾股定理,得OD==3,
∵点A在第二象限,∴A(-3,4),
将A(-3,4)代入y=,得m=-3×4=-12,
∴反比例函数的解析式为y=-,
将B(n,-2)代入y=-,得n=6,
∴B(6,-2),
将A(-3,4),B(6,-2)代入y=kx+b,
得,解得,
∴一次函数的解析式为y=-x+2;
(2)请直接写出满足kx+b>的x的取值范围;
解:(2)由图象知,满足kx+b>的x的取值范围为x<-3或0<x<6;
(3)E是y轴上一点,且△AOE是等腰三角形,求出所有符合条件的点E的坐标.
解:(3)设点E的坐标为(0,a),
∵A(-3,4),O(0,0),
∴OE=|a|,OA=5,AE=,
由△AOE是等腰三角形,则:
①当OA=OE时,|a|=5,∴a=±5,
∴E(0,5)或(0,-5);
②当OA=AE时,5=,
∴a=8或a=0(舍),∴E(0,8);
③当OE=AE时,|a|=,
∴a=,∴E(0,),
综上所述,满足条件的点E的坐标为(0,5)或(0,-5)或(0,8)或(0,).
谢 谢 观 看
第3课时 锐角三角函数(2)
第24章 解直角三角形
一、选择题
1.已知∠A是锐角,tanA=1,那么∠A的度数是( C )
A.15° B.30° C.45° D.60°
2.在Rt△ABC中,∠C=90°,∠A=60°,则sinA+cosB的值为( B )
A. B. C. D.
3.已知α为锐角,且sin(α-10°)=,则α=( A )
A.70° B.60° C.50° D.30°
C
B
A
4.在△ABC中,若|sinA-|+(-cosB)2=0,∠A,∠B都是锐角,则∠C=( C )
A.75° B.90° C.105° D.120°
C
二、填空题
5.在Rt△ABC中,∠C=90°,AB=2,AC=,则∠B的度数为 60° .
6.在△ABC中,sinB=cos(90°-∠C)=,则∠A的度数是 120° .
60°
120°
三、解答题
7.计算:
(1)cos30°+sin45°;
解:原式=×+×
=+1
=.
(2)·tan 30°;
解:原式=×
=××
=.
(3)(sin60°+cos45°)(sin60°-cos45°);
解:原式=sin260°-cos245°
=()2-()2
=-
=.
(4)6tan230°-sin60°-2sin45°;
解:原式=6×()2-×-2×
=2--
=-.
(5);
解:原式=
=-×
=.
(6)tan30°-+tan45°·cos45°.
解:原式=-(-1)+
=-+1+.
8.设β为锐角,且x2+2x+sinβ=0的两根之差为,求β的度数.
解:设方程x2+2x+sinβ=0的两根为x1,x2,
由根与系数的关系知x1+x2=-2,x1x2=sinβ,
由题意知:|x1-x2|=,
∴=-4x1x2=4-4sinβ=2,
解得sinβ=,
∴β=30°.
一、填空题
9.如图(a)是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图(b),再沿BF折叠成图(c),则图(c)中的tan∠DHF的值是 .
第9题图
二、解答题
10.A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道将A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:≈1.414,≈1.732)
第10题图
解:如图,过点C作CD⊥AB于点D,
∵AC=20km,∠CAB=30°,
∴ CD=AC=10km,
AD=AC=10km,
∵∠CBA=45°,
∴BD=CD=10km,BC=CD≈14.14km,
∴AB=AD+BD=10+10≈27.32km,
则AC+BC-AB≈20+14.14-27.32≈6.8km,
答:从A地到B地的路程将缩短约6.8km.
解答题
11.亲爱的同学们,在我们进入高中以后,将会学到三角函数公式:sin(α+β)=sinαcosβ+cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ.
例如:sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°=.
(1)试仿照例题,求出cos75°的准确值;
解:(1)cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin 45°=×-×=;
(2)我们知道tanα=,试求出tan75°的准确值;
解:(2)tan75°===2+;
(3)根据所学知识,请你巧妙地构造一个合适的直角三角形,求出tan75°的准确值(要求分母有理化),和(2)中的结论进行比较.
解:(3)如图,
tan75°=tan∠CBD===+2,
与(2)中的结论一致.
谢 谢 观 看
第4课时 锐角三角函数(3)
第24章 解直角三角形
一、选择题
1.sin240°+cos240°的值为( C )
A.0 B. C.1 D.2
2.如果α是锐角,且sinα=,那么cos(90°-α)的值为( B )
A. B. C. D.
C
B
3.如果锐角α的正弦值为,那么下列结论正确的是( C )
A.α=30° B.α=45°
C.30°<α<45° D.45°<α<60°
C
二、填空题
4.比较大小:(填“>”“<”或“=”)
(1)cos27° > cos63°;
(2)sin44° < cos44°.
5.已知∠A为锐角,且cosA≤,那么∠A度数的取值范围是 60°≤∠A<90° .
6.已知α为锐角,如果sinα+cosα=,那么sinα·cosα= .
>
<
60°≤∠A<90°
三、解答题
7.已知tanα=,α是锐角,求tan(90°-α),sinα,cosα的值.
解:如图,∵tanB=tanα=,
∴设AC=2x,BC=5x,
则AB=x,
∴tan(90°-α)==,
sinα===,
cosα===.
8.根据三角函数规律比较大小.
(1)比较sin46°和cos20°的大小;
解:∵sin46°=cos44°,且44°>20°,
∴cos44°<cos20°,
即sin46°<cos20°.
(2)比较sin20°、cos60°和tan45°的大小;
解:∵sin20°=cos70°,70°>60°,
∴cos70°<cos60°=,
∵tan45°=1,
∴cos70°<cos60°<tan45°,
即sin20°<cos60°<tan45°.
(3)比较sin20°、cos80°和tan45°的大小.
解:∵sin20°=cos70°,80°>70°,tan45°=1,
∴cos80°<cos70°<cos60°<tan45°,
即cos80°<sin 20°<tan45°.
9.计算:sin266°-tan54°tan36°+sin224°+sin230°+cos230°+.
解:原式=sin266°+sin224°-1+1+
=sin266°+cos266°+9
=10.
一、填空题
10.若α是锐角,=1+,则α的度数为 40° .
40°
二、解答题
11.(1)若α为锐角,且sinα+cosα=,求sinα-cosα的值;
解:∵(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+2sinαcosα,sinα+cosα=,
∴1+2sinαcosα=,
∴2sinαcosα=,
∴(sinα-cosα)2=sin2α+cos2α-2sinαcosα=1-=,
∵α为锐角,∴sinα-cosα=±.
(2)已知sina,cosa是关于x的方程8x2+6mx+2m+1=0的两根,求+的值.
解:由根与系数的关系,
得sina+cosa=-,sina·cosa=,
∵(sina+cosa)2=1+2sina·cosa,
∴=1+2×,解得m=2或-,
∵Δ=36m2-4×8×(2m+1)
=4(9m2-16m-8),
当m=2时,Δ=-16<0,故舍去,
当m=-时,Δ=>0,
∴m=-,
∴+==-=-.
解答题
12.如图,海中有一个小岛A,该岛的四周10海里的范围内有暗礁.有一货轮在海面上由西向东航行,到达B处时,该货轮位于小岛南偏西60°的方向上,再往东行驶20海里后到达小岛的南偏西30°的方向上的C处,如果货轮继续向东航行,是否会有触礁的危险?请通过计算说明.
第12题图
解:如图,过点A作AD⊥BC交BC延长线于点D,
由题意,得∠BAD=60°,∠CAD=30°,
∴∠BAC=∠BAD-∠CAD=30°,
又∵∠B=90°-∠BAD=90°-60°=30°,
∴∠B=∠BAC,∴AC=BC=20海里,
在Rt△ACD中,
AD=AC·cos∠CAD=10海里,
由题意知,以海岛A为圆心,10海里为半径的范围内有暗礁,
∵AD=10海里>10海里,
∴如果货轮继续向东航行,没有触礁的危险.
谢 谢 观 看
第5课时 专题锐角三角函数
第24章 解直角三角形
解答题
1.如图,在Rt△ABC中,∠C=90°,AB=10,tanA=,求BC的长和sinB的值.
第1题图
解:∵tanA==,
∴AC=2BC,
在Rt△ABC中,
AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sinB===.
2.如图,在△ABC中,∠B=30°,tanC=,AD⊥BC于点D.若AB=8,求BC的长.
第2题图
解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ADB中,
∠B=30°,AB=8,
∴AD=4,BD=4,
在Rt△ADC中,tanC=,AD=4,
∴CD==3,
∴BC=BD+CD=4+3.
3.如图,在Rt△BCD中,∠BDC=30°,延长CD到点A,连接AB,∠A=15°,求tan15°的值.(结果保留根号)
第3题图
解:∵∠A=15°,∠BDC=30°,
∴∠ABD=15°,
∴AD=BD,
设BC=x,
在Rt△BDC中,∵∠BDC=30°,∴BD=2x,
∴DC==x,
∴AD=BD=2x,AC=AD+DC=(2+)x,
在Rt△ABC中,
tan15°===2-.
4.如图,在△ABC中,BC=AC,∠BCA=135°,求tanA的值.
第4题图
解:如图,过点B作BD⊥AC交AC的延长线于点D,
∵∠BCA=135°,∴∠BCD=45°,
∴BD=CD=BC=AC,
∴AD=AC+CD=2AC,
∴tanA==.
5.在Rt△ABC中,∠C=90°,斜边c=5,两直角边a、b是关于x的一元二次方程x2-mx+2m-2=0的两个根,求Rt△ABC中较大锐角的三个三角函数值.
解:由题意得:a+b=m,ab=2m-2,且a2+b2=c2,
∴-2ab=c2,
即m2-2=25,
解得m1=7,m2=-3,
当m=-3时,ab=-8(舍去),∴m=7,
∴,解得:或,
故Rt△ABC中较大锐角为边长为4的边所对的角,设为α,则sinα=,cosα=,tanα=.
6.如图,在△ADC中,∠A=30°,∠ACD=90°,B在AC上,∠DBC=45°,E在BC的延长线上,且AB=2,CE=3,过E作EF⊥AE,交BD的延长线于F,求EF的长.
第6题图
解:设BC=x,
∵∠DBC=45°,∠ACD=90°,EF⊥AE,
∴EF=BE=3+x,BC=DC=x,
∴AC=2+x,
∵∠A=30°,tanA=,
∴2+x=x,∴x=+1,
∴EF=+4.
7.如图,在△ABC中,∠C=90°,AB=10,sinB=,点D为边BC的中点.
(1)求BC的长;
解:(1)∵∠C=90°,sinB==,AB=10,
∴AC=6,∴由勾股定理可知:BC=8;
第7题图
(2)求∠BAD的正切值.
解:(2)如图,过点D作DE⊥AB,垂足为E,
∵∠C=∠BED=90°,∠B=∠B,
∴△BED∽△BCA,
∴==,
即==,
∴BE=,ED=,
∴AE=AB-BE=10-=,
∴tan∠BAD==.
8.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠DCB=.
(1)求cosB的值;
解:(1)如图,过点A作AE⊥BC于点E,
∵AB=AC=5,
∴BE=CE=BC=×8=4,
在Rt△ABE中,cosB==;
第8题图
(2)求△BCD的面积.
解:(2)如图,过点D作DF⊥BC于点F,
在Rt△CDF中,tan∠DCF==,
设DF=3x,则CF=5x,
在Rt△ABE中,AE==3,
∴tanB==,
在Rt△BDF中,tanB==,
∴BF=4x,
∴BC=BF+CF=4x+5x=9x,
即9x=8,解得x=,
∴DF=3x=,
∴S△BCD=DF·BC=××8=.
谢 谢 观 看
第6课时 解直角三角形(1)
第24章 解直角三角形
一、选择题
1.在Rt△ABC中,∠C=90°,若BC=1,AB=,则tanA的值为( C )
A. B.
C. D.2
2.在Rt△ABC中,∠C=90°,若a=6,∠B=30°,则c和tanA的值分别为( C )
A.12, B.12,
C.4, D.2,
C
C
3.在△ABC中,∠C=90°,下列结论正确的是( D )
A.AC=BC·tanA B.AB=AC·cosA
C.AC=AB·sinA D.AC=BC·tanB
D
二、填空题
4.在△ABC中,∠C=90°,BC=4,sinA=,则AB= 12 .
5.等腰三角形底边与底边上的高的比是2∶,则顶角为 60° .
12
60°
三、解答题
6.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近.为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从船队首(点O)尾(点A)出发前去拦截,4分钟后同时到达点B将可疑快艇驱离.已知OA=20海里,甲直升机每小时飞行180海里,航向为北偏东25°,乙直升机的航向为北偏西65°,求乙直升机的飞行速度.
第6题图
解:由题意得:∠B=25°+65°=90°,
∵OA=20海里,OB=180×=12海里,
∴AB===16海里,
∴16÷=240海里/小时,
答:乙直升机的飞行速度为每小时飞行240海里.
7.如图,有一轮船在A处测得南偏东30°方向上有一小岛F,轮船沿正南方向航行至B处,测得小岛F在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛F在正东方向上,求A,B之间的距离.(结果保留根号)
第7题图
解:在Rt△BCF中,∠CBF=45°,
∴CF=BC=10海里,
在Rt△ACF中,∠CAF=30°,
AC==10海里,
∴AB=AC-BC=10(-1)海里,
答:A,B之间的距离为10(-1)海里.
8.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tanB=.
(1)求AD的长;
解:(1)在Rt△ABC中,tanB==,
∴AC=3x,BC=4x,
∵AC2+BC2=AB2,
∴(3x)2+(4x)2=52,
解得x=1或-1(舍去),
∴AC=3,BC=4,
∵BD=1,∴CD=3,
∴AD==3;
第8题图
(2)求sinα的值.
解:(2)如图,过点D作DE⊥AB于点E,
∵tanB=,
∴设DE=3y,BE=4y,
∵BE2+DE2=BD2,
∴(3y)2+(4y)2=12,
解得y=或-(舍去),
∴DE=,∴sinα==.
一、填空题
9.如图,在Rt△ABC中,∠C=90°,点D是AB的中点,ED⊥AB交AC于点E.设∠A=α,且tanα=,则tan2α= .
第9题图
二、解答题
10.如图,一艘游艇在离开码头A处后,沿南偏西60°方向行驶到达B处,此时从B处发现灯塔C在游轮的东北方向,已知灯塔C在码头A的正西方向200米处,求此时游轮与灯塔C的距离.(精确到1米,参考数据:≈1.414,≈1.732,≈2.449)
第10题图
解:如图,过B作BD⊥AC交AC的延长线于D,
在Rt△BCD中,∠D=90°,∠DBC=45°,
∴∠DCB=∠DBC=45°,BD=CD,
在Rt△ABD中,∠DAB=30°,
∴AD=BD,
∵AC=200米,
∴BD-BD=200,
∴BD==100(+1)米,
∴BC=BD=100(+1)×≈386米,
答:此时游轮与灯塔C的距离约为386米.
解答题
11.如图,一艘船由A港沿北偏东65°方向航行90km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
第11题图
解:由题意得,∠CAB=65°-20°=45°,∠C=40°+20°=60°,AB=90km,
如图,过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∠EAB=45°,
∴AE=BE=AB=90km,
在Rt△CBE中,∠C=60°,
∴CE=BE=30km,
∴AC=AE+CE=(90+30)km,
∴A,C两港之间的距离为(90+30)km.
谢 谢 观 看
第7课时 解直角三角形(2)
第24章 解直角三角形
一、选择题
1.如图,某地修建高速公路,要从B地向C地修一条隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( A )
第1题图
A
A.100m B.50m
C.50m D.m
2.如图,在楼顶点A处观察旗杆CD测得旗杆顶部C的仰角为30°,旗杆底部D的俯角为45°.已知楼高AB=9m,则旗杆CD的高度为( B )
第2题图
A.(9+)m B.(9+3)m
C.9m D.12m
B
二、填空题
3.如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度约为 15.3 米.(结果保留一位小数,参考数据:sin54°≈0.8090,cos54°≈0.5878,tan54°≈1.3764)
第3题图
15.3
三、解答题
4.我市某建筑工地,欲拆除该工地的一危房AB(如图),准备对该危房实施定向爆破.已知距危房AB水平距离60米处有一居民住宅楼CD,该居民住宅楼CD高15米,在该住宅楼顶C处测得此危房屋顶A的仰角为30°,请你通过计算说明在实施定向爆破危房AB时,该居民住宅楼CD有无危险?(在地面上以点B为圆心,AB长为半径的圆形区域为危险区域,参考数据:≈1.414,≈1.732)
第4题图
解:在Rt△AEC中,∠ACE=30°,CE=BD=60米,
∴AE=CE·tan∠ACE≈34.64米,
又∵BE=CD=15米,
∴AB=AE+BE≈49.64米,
∵60>49.64,即BD>AB,
∴在实施定向爆破危房AB时,该居民住宅楼CD没有危险.
5.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者,在消防车上点A处测得点B和点C的仰角分别为45°和65°,点A距地面2.5米,点B距地面10.5米,为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数,参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,≈1.4)
第5题图
解:如图,作AH⊥CN于点H,
在Rt△ABH中,∠BAH=45°,
∴AH=BH=10.5-2.5=8米,
在Rt△AHC中,∠CAH=65°,
∴CH=AH·tan65°≈17米,
∴BC=CH-BH=17-8=9米,
答:云梯需要继续上升的高度BC约为9米.
解答题
6.如图,学校教学楼上悬挂一块长为3m的标语牌CD.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离,测角仪支架高AE=BF=1.2m,小明在E处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由.(图中点A,B,C,D,E,F,H在同一平面内,精确到0.1m,参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
第6题图
解:能.
如图,延长EF交CH于点N,
则∠CNF=90°,
∵∠CFN=45°,∴CN=NF,
设DN=xm,
则NF=CN=(x+3)m,
∴EN=5+(x+3)=(x+8)m,
在Rt△DEN中,DN=EN·tan∠DEN,
即x=(x+8)·tan31°,解得x≈12.0,
则DH=DN+NH≈12.0+1.2=13.2m,
答:点D到地面的距离DH的长约为13.2m.
解答题
7.如图,码头A、B分别在海岛O的北偏东45°和北偏东60°方向上,仓库C在海岛O的北偏东75°方向上,码头A、B均在仓库C的正西方向,码头B和仓库C的距离BC=50km,现将一批物资从仓库C用汽车运送到A、B两个码头中的一处,再用货船运送到海岛O,若汽车的行驶速度为50km/h,货船航行的速度为25km/h,问这批物资在哪个码头装船,最早运抵海岛O?(两个码头物资装船所用的时间相同,参考数据:≈1.4,≈1.7)
第7题图
解:如图,延长CA交OM于K,
由题意得:∠COK=75°,∠BOK=60°,∠AOK=45°,∠CKO=90°,
∴∠KCO=15°,∠KBO=30°,OK=KA,
∵∠KBO=∠C+∠BOC,
∴∠C=∠BOC=15°,
∴OB=BC=50km,
在Rt△OBK中,OK=OB=25km,
KB=OK=25≈42.5km,
在Rt△AOK中,AK=25km,OA=25≈35km,
∴AB=KB-AK≈17.5km,∴AC≈67.5km,
∴在码头A装船运抵海岛O的用时为:
+=2.75h,
在码头B装船船运抵海岛O的用时为:
+=3h,
∵2.75<3,
∴这批物资在码头A装船,最早运抵海岛O.
谢 谢 观 看
第8课时 解直角三角形(3)
第24章 解直角三角形
一、选择题
1.如图,某停车场入口的栏杆,从水平位置AB绕点O旋转到A'B'的位置,已知AO=4米,若栏杆的旋转角∠AOA'=50°,则栏杆A端升高的高度是( B )
第1题图
B
A.米 B.4sin50°米
C.米 D.4cos50°米
2.如图,要测量小河两岸相对的两点P、A之间的距离,可以在小河边PA的垂线PB上取一点C.测得PC=80米,∠PCA=32°,则PA的长为( B )
第2题图
A.80sin32°米 B.80tan32°米
C.米 D.米
B
3.河堤横断面如图所示,AB=10米,tan∠BAC=,则AC的长为( A )
第3题图
A.5米 B.10米 C.15米 D.10米
A
4.如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒,若∠BAC=α,则此车的速度为( A )
第4题图
A.5tanα米/秒 B.80tanα米/秒
C.米/秒 D.米/秒
A
二、填空题
5.(1)小明沿着坡度i=1∶2.5的斜坡前行了29米,那么他上升的高度是 2 米;
(2)有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1∶2.5,那么该斜坡的水平距离AC的长为 75 m.
2
75
6.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成角为32°,缆车速度为每分钟50米,从山脚下A处到达山顶B处缆车需要16分钟,则山的高度BC约为 424 米.(精确到1米,参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249)
第6题图
424
三、解答题
7.如图,扶梯AB的坡比为1∶2,滑梯CD的坡比为1∶.若AE=40m,BC=30m,某人从扶梯上去,经过顶部BC,再沿滑梯滑下,求此人经过的路径长.(结果精确到0.1m,参考数据:≈1.41,≈1.73,≈2.24)
第7题图
解:∵BE∶AE=1∶2,AE=40m,∴BE=20m,
∴AB==20m,
∵CF∶DF=1∶,CF=BE=20m,
∴FD=CF=20m,
∴CD==40m,
∴经过的路径长为AB+BC+CD=20+30+40=70+20≈114.8m,
答:此人经过的路径长约为114.8m.
8.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面示意图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=AC=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长.(结果保留根号)
第8题图
解:如图,延长BA交FD的延长线于点G,过点A作AH⊥DG于点H,
由题意知,AB=300cm,BE=AC=50cm,AH=50cm,∠AGH=30°,
∴在Rt△AGH中,AG=2AH=100cm,
∴CG=AC+AG=150cm,
则CD=CG=75cm,
∵EG=AB-BE+AG=300-50+100=350cm,
∴在Rt△EFG中,
EF=EG·tan∠EGF=cm,
∴支撑角钢CD的长为75cm,EF的长为cm.
解答题
9.如图,在岷江的右岸边有一高楼AB,左岸边有一坡度i=1∶2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行走20m到达D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.(结果保留根号)
第9题图
解:在Rt△DEC中,i==,
∵DE2+EC2=CD2,CD=20m,
∴DE2+(2DE)2=(20)2,
∴DE=20m,∴EC=40m,
如图,作DG⊥AB于点G,作CH⊥DG于点H,
则四边形DEBG、四边形DECH、四边形BCHG都是矩形,
∵∠ACB=45°,AB⊥BC,∴AB=BC,
设AB=BC=xm,
则AG=(x-20)m,DG=(x+40)m,
在Rt△ADG中,=tan∠ADG,∠ADG=30°,
∴=,解得:x=50+30,
答:楼AB的高度为(50+30)m.
谢 谢 观 看
第9课时 专题解直角三角形的应用
第24章 解直角三角形
解答题
1.2023年12月2日是第十二个“全国交通安全日”,主题为“文明守法平安回家”.如图,某观测点设在距高速公路(直线l)100m的P处,一辆轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3s,并测得∠AOP=90°,∠APO=60°,∠BPO=45°,试判断此车是否超过了25m/s的限制速度?(≈1.732)
第1题图
解:由题意得PO=100m,
∵∠PBO=45°,∴BO=PO=100m,
∵∠APO=60°,∴AO=OPtan60°=100m,
∴AB=AO-BO=(100-100)m,
∴此车的速度为≈24.4m/s,
∵24.4m/s<25m/s,
∴此车速度没有超过25m/s的限制速度.
2.商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,扶梯AB的坡度i为1∶,改造后的斜坡式自动扶梯的坡角∠ACB为15°.
(1)求AD的长度;
解:(1)由题意得tan∠ABD=,∴∠ABD=30°,
∴在Rt△ADB中,AD=AB=5m;
第2题图
(2)求改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
解:(2)在Rt△ACD中,sin∠ACD=,
∴AC=≈≈19.2m,
答:改造后的自动扶梯AC的长约为19.2m.
3.如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要从B地绕行.已知B地位于A地的北偏东67°方向,距离A地520km,C地位于B地的南偏东30°方向,若打通穿山隧道,建成A、C两地直达高铁,求A地到C地之间直线高铁线路的长.(结果保留整数,参考数据:sin67°≈,cos67°≈,tan67°≈,≈1.73)
第3题图
解:如图,过点B作BD⊥AC于点D,
在Rt△ABD中,∵∠ABD=67°,AB=520km,
∴AD=ABsin67°≈480km,
BD=ABcos67°≈200km,
∵∠CBD=30°,∴CD=BDtan30°≈115.3km,
∴AC=AD+CD≈480+115.3≈595km,
∴A地到C地之间直线高铁线路的长约是595km.
4.如图1是一个手机支架,图2是其侧面示意图,AB、BC可分别绕点A、B转动,测量知AB=10cm,BC=8cm.当AB,BC转动到∠BAE=70°,∠ABC=65°时,求点C到直线AE的距离.(精确到0.1cm,参考数据:sin70°≈0.94,cos70°≈0.34,≈1.41)
第4题图
解:如图,过点B作BM⊥AE于点M,过点C作CN⊥AE于点N,CD⊥BM于点D,
∴四边形MNCD是矩形,∴DM=CN,
在Rt△ABM中,∠BAE=70°,AB=10cm,
∴∠ABM=20°,BM=ABsin70°≈9.4cm,
∵∠ABC=65°,∴∠CBD=∠ABC-∠ABM=45°,
∴BD=BCcos45°≈5.64cm,
∴CN=DM=BM-BD≈3.8cm,
∴点C到AE的距离约为3.8cm.
5.如图,某建筑物楼顶挂有广告牌BC,小华从点A处沿坡度i=1∶的斜坡步行30米到达点P处,测得广告牌底部C的仰角为45°,广告牌顶部B的仰角为53°,小华的身高忽略不计,已知广告牌BC=12米.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
(1)求点P处距离水平地面的高度;
第5题图
解:(1)如图,过点P作PE⊥AO于点E,
∵坡度i=1∶,
∴tan∠PAE==,∴∠PAE=30°,
∴PE=AP=15米,
即点P处距离水平地面的高度为15米;
(2)求建筑物OC的高度.
解:(2)如图,过点P作PF⊥BO于点F,
∵∠CPF=45°,∠BPF=53°,
∴CF=PF,BF=PF·tan53°≈1.3PF,
∵BC=BF-CF=12米,
∴1.3PF-PF=12,∴PF=CF=40米,
∴OC=CF+OF=CF+PE=55米,
即建筑物OC的高度约为55米.
解答题
6.如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到点D处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,无人机的高度为(30+15)米.(结果保留根号,参考数据:tan75°=2+,tan15°=2-)
(1)求小区楼房BC的高度;
第6题图
解:(1)如图,过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,则四边形BCFE是矩形,
由题意得:AB=45米,DE=(30+15)米,∠DAE=75°,∠DCF=∠FDC=45°,∴CF=DF=BE,
在Rt△ADE中,tan∠DAE==2+,
∴AE==15米,∴BE=DF=AB-AE=30米,
∴EF=DE-DF=15米,
答:小区楼房BC的高度为15米;
(2)若无人机以5米/秒的速度继续沿平行于AB的路线向右匀速飞行.问:经过多少秒,无人机刚好离开操控者的视线?
解:(2)如图,作DG∥AB,交AC的延长线于点G,作GH⊥AB于点H,
∵BC∥GH,∴=,
∴=,∴AH=(30+45)米,
∴DG=EH=AH-AE=(30+30)米,
(30+30)÷5=(6+6)秒,
答:经过(6+6)秒,无人机刚好离开操控者的视线.
解答题
7.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠得到△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
由折叠得,∠BFE=∠C=90°,
∴∠AFB+∠DFE=∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,∴△ABF∽△DFE;
第7题图
(2)若sin∠DFE=,求tan∠EBC的值;
(2)解:在Rt△DEF中,sin∠DFE==,
∴设DE=a,EF=3a,则DF=2a,
由折叠得,∠EBC=∠EBF,CE=EF=3a,
∴AB=CD=DE+CE=4a,
由(1)得:△ABF∽△DFE,∴==,
∴tan∠EBC=tan∠EBF==;
(3)若AF=5cm,BF=10cm,动点M从点B出发,在BF上以每秒2cm的速度向点F匀速运动,同时动点N从点A出发,在AB上以每秒cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN,当△ABF与△BMN相似时,求t的值.
(3)解:∵AF=5cm,BF=10cm,∴AB=5cm,
由题意得,BM=2tcm,BN=(5-t)cm,
①当△NBM∽△ABF时,=,
即=,解得t=;
②当△MBN∽△ABF时,=,
即=,解得t=,
综上所述,t的值为或.
谢 谢 观 看
第10课时 复习巩固
第24章 解直角三角形
一、选择题
1.在△ABC中,∠C=90°,BC=3,tanA=,则边AB的长是( D )
A. B.3 C.4 D.5
2.已知α为锐角,且cos(α-20°)=,那么α的度数为( C )
A.70° B.60° C.50° D.30°
D
C
3.下列各式中,不成立的是( D )
A.sin230°+cos230°=1
B.sin15°=cos75°
C.tan30°·tan60°=1
D.cos60°=2sin30°
4.若α为锐角,cos(α+60°)=0.4,则( A )
A.0°<α<30° B.30°<α<45°
C.45°<α<60° D.60°<α<90°
D
A
二、填空题
5.已知CD是Rt△ABC的斜边AB上的中线,若∠A=35°,则∠BCD= 55° .
6.如图,△ABC中,∠ACB=90°,∠A=30°,AB=4,若CD是高,则BD= 1 .
第6题图
55°
1
7.一山坡的坡度i=1∶3,小刚从山坡脚下点P处上坡走了50米到达点N处,那么他上升的高度是 50 米.
50
三、解答题
8.计算:3tan30°-+cos45°+.
解:原式=3×-2+×+
=-2+2+-1
=2-1.
9.在全校的科技制作大赛中,王浩同学用木板制作了一个带有卡槽的三角形手机架.如图所示,卡槽的宽度DF与内△ABC的AB边长相等.已知AC=20cm,BC=18cm,∠ACB=50°,一个手机的最长边为17cm,王浩同学能否将此手机立放入卡槽DF内?请说明理由.(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
第9题图
解:王浩同学能将手机放入卡槽DF内,理由如下:
如图,作AD⊥BC于点D,
∵∠C=50°,AC=20cm,
∴AD=AC·sin50°≈20×0.8=16cm,
CD=AC·cos50°≈20×0.6=12cm,
∴DB=BC-CD=18-12=6cm,
∴AB===cm,
∴DF=AB=cm,
∵17=<,
∴王浩同学能将手机放入卡槽DF内.
一、选择题
10.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是边AB的中点,AB=10,DE=4,则S△AEC=( B )
A.8
B.7.5
C.7
D.6
第10题图
B
11.规定:对任意角x,y,都有sin2x+cos2x=1,sin(-x)=-sinx,cos(-x)=cosx,cos(x+y)=cosxcosy-sinxsiny,现给出下列等式:①sin(-60°)=-;②cos15°=;③cos2x=1-2sin2x;④cos(x-y)=cosxcosy+sinxsiny;⑤cosxcosy=[cos(x+y)+cos(x-y)],其中等式成立的有( C )
A.2个 B.3个 C.4个 D.5个
C
二、解答题
12.某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到点C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命迹象所在点C处的深度.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
第12题图
解:如图,过点C作CD⊥AB,交AB的延长线于点D,
设CD=x米,
在Rt△ACD中,∠CAD=30°,
∴AD=CD=x米,
在Rt△BCD中,∠CBD=45°,
∴BD=CD=x米,由题意得x-x=6,
解得:x=3(+1)≈8.2,
答:生命迹象所在点C的深度为8.2米.
解答题
13.如图,港口B位于港口A的南偏西45°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的南偏东45°方向的D处,它沿正北方向航行18.5km到达E处,此时测得灯塔C在E处的南偏西70°方向上,求E处距离港口A有多远?(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
第13题图
解:如图,过点B作BM⊥AD,垂足为点M,过点C作CN⊥AD,垂足为点N,
设CN=x km,
在Rt△ACN中,∠A=45°,
∴AN===xkm,
在Rt△ECN中,∠CEN=70°,
∴EN==km,
∵CN⊥AD,BM⊥AD,
∴CN∥BM,
∴==,
又∵C为AB的中点,
∴AB=2AC,AC=BC,
∴BM=2CN=2xkm,AN=MN=xkm,
由题可知,∠MDB=45°,
在Rt△BMD中,∠MDB=45°,
∴DM===2xkm,
∵DE-DM-EN=MN,
∴18.5-2x-=x,
∴x=≈5.5,
∴AE=AN-EN≈5.5-≈3.5km,
答:E处距离港口A约3.5km.
谢 谢 观 看
