上海市各区县2016届高三上学期期末考试数学理试题汇编:立体几何
文档属性
| 名称 | 上海市各区县2016届高三上学期期末考试数学理试题汇编:立体几何 |

|
|
| 格式 | zip | ||
| 文件大小 | 503.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-03 00:00:00 | ||
图片预览




文档简介
上海市各区县2016届高三上学期期末考试数学理试题汇编
立体几何
一、填空题
1、(宝山区2016届高三上学期期末)等腰直角三角形的直角边长为1,则绕斜边旋转一周所形成的几何体的体积为
2、(崇明县2016届高三上学期期末)已知圆锥的母线长为5cm,侧面积为15cm2,则此圆锥的体积是____________ cm3 .
3、(虹口区2016届高三上学期期末)如图所示,半径的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于__________
4、(黄浦区2016届高三上学期期末)若将两个半径为的铁球熔化后铸成一个球,则该球的半径为 .
5、(嘉定区2016届高三上学期期末)在正方体中,为棱的中点,则异面直线与所成的角的大小为__________________(结果用反三角函数值表示).
6、(嘉定区2016届高三上学期期末)在若圆锥的底面周长为,侧面积也为,则该圆锥的体积为______________.
7、(静安区2016届高三上学期期末)已 ( http: / / www.21cnjy.com )知球的半径为24cm,一个圆锥的高等于这个球的直径,而且球的表面积等于圆锥的表面积,则这个圆锥的体积是 cm3.
8、(闵行区2016届高三上学期期末)若一圆锥的底面半径为,体积是,则该圆锥的侧面积等于 .
9、(浦东新区2016届高三上学期期末)如图,已知正方体,,为棱的中点,则与平面所成的角为 (结果用反三角表示)
10、(普陀区2016届高三上学期期末)若正六棱柱的底面边长为10,侧面积为180,则这个棱柱的体积为_________
11、(青浦区2016届高三上学期期末)平面直角坐标系中,方程的曲线围成的封闭图形绕轴旋转一周所形成的几何体的体积为
12、(松江区2016届高三上学期期末)若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为、则有 ▲
13、(徐汇区2016届高三上学期期末)已知四面体的外接球球心在棱上,,,则、两点在四面体的外接球上的球面距离是________________.
14、(闸北区2016届高三上学期期末)一 ( http: / / www.21cnjy.com )个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是
填空题参考答案:
1、 2、12 3、 4、 5、
6、 7、 12288 8、 9、.(,)
10、450 11、 12、 13、 14、
二、选择题
1、(宝山区2016届高三上学期期末)若是异面直线,则下列命题中的假命题为--------- ( )
(A)过直线可以作一个平面并且只可以作一个平面与直线平行;
(B)过直线至多可以作一个平面与直线垂直;
(C)唯一存在一个平面与直线等距;
(D)可能存在平面与直线都垂直。
2、(嘉定区2016届高三上学期期末)下列四个命题:
①任意两条直线都可以确定一个平面;
②若两个平面有个不同的公共点,则这两个平面重合;
③直线,,,若与共面,与共面,则与共面;
④若直线上有一点在平面外,则在平面外.
其中错误命题的个数是( )
A. B. C. D.
3、(静安区2016届高三上学期期末)下列四个命题中,真命题是 ( )
A.和两条异面直线都相交的两条直线是异面直线;
B.和两条异面直线都垂直的直线是异面直线的公垂线;
C.和两条异面直线都相交于不同点的两条直线是异面直线;
D.若a、b是异面直线, b、c是异面直线,则a、c是异面直线.
4、(普陀区2016届高三上学期期末)如图,在四面体中,AB⊥BD,CD⊥DB,若与所成的角的大小为,则二面角C-BD-A的大小为( )
A. 或
B. 或
C. 或
D. 或
5、(徐汇区2016届高三上学期期末)在正方体中,、分别是棱、的中点,、分别是线段与上的点,则与平面平行的直线有
0条
1条
2条
无数条
6、(杨浦区2016届高三上学期期末)对于两个平面和两条直线, 下列命题中真命题是 ( )
A.若, , 则
B.若, , 则
C. 若,,,则
D. 若,,,则
7、(闸北区2016届高三上学期期末)已知是两条不同直线,是两个不同平面,给出下列四个命题:
① 若垂直于同一平面,则与平行;
② 若平行于同一平面,则与平行;
③ 若不平行,则在内不存在与平行的直线;
④ 若不平行,则与不可能垂直于同一平面
其中真命题的个数为( )
A. 4 B. 3 C. 2 D. 1
选择题参考答案:
1、D 2、C 3、C 4、C 5、D 6、D 7、D
三、解答题
1、(宝山区2016届高三上学期期末)在三棱锥中,已知PA,PB,PC两两垂直,PB=5,PC=6,三棱锥的体积为20,Q是BC的中点,求异面直线PB,AQ所成角的大小(结果用反三角函数值表示)。
( http: / / www.21cnjy.com )
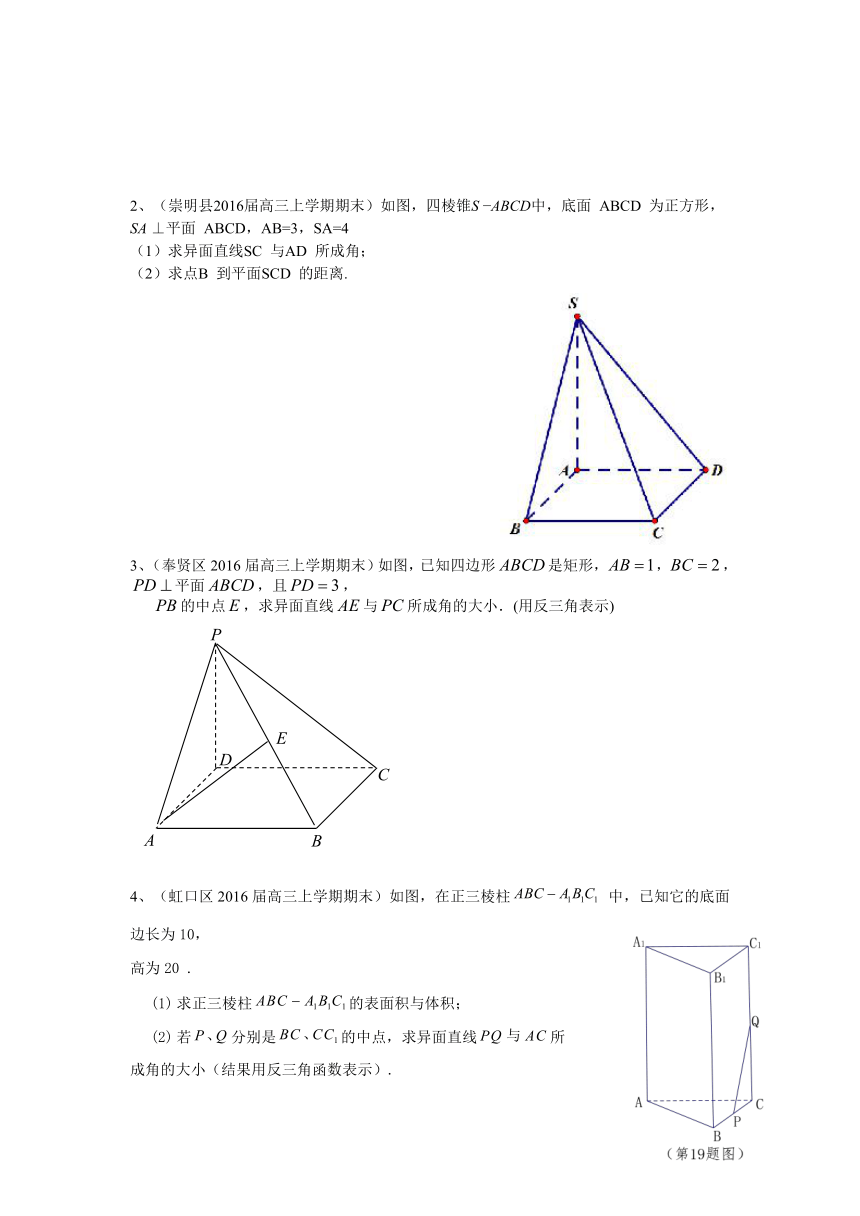
2、(崇明县2016届高三上学期期末)如图,四棱锥S ABCD中,底面 ABCD 为正方形,SA ⊥平面 ABCD,AB=3,SA=4
(1)求异面直线SC 与AD 所成角;
(2)求点B 到平面SCD 的距离.
( http: / / www.21cnjy.com )
3、(奉贤区2016届高三上学期期末)如图,已知四边形是矩形,,,平面,且,
的中点,求异面直线与所成角的大小.(用反三角表示)
4、(虹口区2016届高三上学期期末)如图,在正三棱柱 中,已知它的底面边长为10,
高为20 .
求正三棱柱的表面积与体积;
若分别是的中点,求异面直线所
成角的大小(结果用反三角函数表示).
5、(黄浦区2016届高三上学期期末) 已知三棱柱的底面为直角三角形,两条直角边和的长分别为4和3,侧棱的长为10.
(1)若侧棱垂直于底面,求该三棱柱的表面积.
(2)若侧棱与底面所成的角为,求该三棱柱的体积.
6、(嘉定区2016届高三上学期期末)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为的正方形,高为,内有深的溶液.现将此容器倾斜一定角度(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(1)要使倾斜后容器内的溶液不会溢出,角的最大值是多少;
(2)现需要倒出不少于的溶液,当时,能实现要求吗?请说明理由.
7、(金山区2016届高三上学期期末)在直三棱柱中,,,且异面直线与所成的角等于,设.
(1) 求的值;
(2) 求三棱锥的体积.
8、(静安区2016届高三上学期期末) 如图,在棱长为1的正方体中,E为AB的中点. 求:
(1)异面直线BD1与CE所成角的余弦值;
(2)点A到平面的距离.
9、(闵行区2016届高三上学期期末)
如图,三棱柱中,侧棱底面,,,,为棱中点,证明异面直线与所成角为,并求三棱柱的体积.
( http: / / www.21cnjy.com )
10、(浦东新区2016届高三上学期期末)
已知交与点,,分别为的中点.
求证:平面.
11、(普陀区2016届高三上学期期末)某种“笼其”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为,高为,圆锥的母线长为.
(1)求这种“笼其”的体积(结果精确到0.1);
(2)现要使用一种纱网材料制作50个“笼其”,该材料的造价为每平方米8元,共需多少元?
( http: / / www.21cnjy.com )
12、(青浦区2016届高三上学期期末)
如图所示,在四棱锥中,,∥且,,点为线段的中点,若,与平面所成角的大小为.
(1)证明:平面;
(2)求四棱锥的体积.
13、(松江区2016届高三上学期期末)
如图,在三棱锥中,平面,,,,分别是的中点.
(1)求三棱锥的体积;
(2)若异面直线与所成的角为,求的值.
14、(徐汇区2016届高三上学期期末)
在三棱锥中,且 .
求证并求三棱锥的体积.
15、(杨浦区2016届高三上学期期末) ( http: / / www.21cnjy.com )如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充。已知金字塔的每一条棱和边都相等
(1) 求证:直线垂直于直线.
若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
解答题参考答案
1、解:,所以,-------------------3分
取PC的中点为D,连结AD,DQ,
则为异面直线PB,AQ所成的角,--------------------------------5分
,,------------------------------------7分
因为,所以----------------------9分
所以
异面直线PB,AQ所成的角为。-----------------------12分
2、
( http: / / www.21cnjy.com )
3、取的中点,连接、
、是中点,是的中位线
∥
(或者其补角)为异面直线与所成角 3分
在中, 5分
6分
,, 7分
由余弦定理可知
10分
11分
异面直线与所成角的大小. 12分
4、解:(1) ……(3分)
……(6分)
(2)连结则又
故等于异面直线所成角. ……(8分)
易得,故
于是异面直线所成角的大小为……(12分)
5、[解](1)因为侧棱底面,所以三棱柱的高等于侧棱的长,
而底面三角形的面积,(2分)
周长,(4分)
于是三棱柱的表面积.(6分)
(2)如图,过作平面的垂线,垂足为,为三棱柱的高.(8分)
因为侧棱与底面所成的角为,所以,可计算得.(9分)
又底面三角形的面积,故三棱柱的体积.(12分)
6、(1)如图③,当倾斜至上液面经过点时,容器内溶液恰好不会溢出,
此时最大. …………………………………………………………………(2分)
解法一:此时,梯形的面积等于(), ………………(3分)
因为,所以,,
即,解得,. ………………(5分)
所以,要使倾斜后容器内的溶液不会溢出,的最大值是. ……………(6分)
解法二:此时,△的面积等于图①中没有液体部分的面积,
即(), ……………………………………………………(3分)
因为,所以,即,
解得,. …………………………………………(5分)
所以,要使倾斜后容器内的溶液不会溢出,的最大值是. …………(6分)
(2)如图④,当时,设上液面为,因为,
所以点在线段上, ………………………………………………………(1分)
此时,,
(), ………………………………………(3分)
剩余溶液的体积为(), …………………………(4分)
由题意,原来溶液的体积为,
因为,所以倒出的溶液不满. …………(5分)
所以,要倒出不少于的溶液,当时,不能实现要求.……(6分)
7、解(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,
即∠A1BC =60,…………………………………………………………………………2分
又AA1⊥平面ABC,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,…………4分
由,,
∴;……………………………………………6分
(2)连接B1C,则三棱锥B1–A1BC的体积等于三棱锥C–A1B1B的体积,
即:,………………………………………………………………9分
△的面积,……………………………………………………………11分
又平面,
所以,所以.………………………………14分
8、解(1)延长DC至G,使CG= DC,连结BG、
,∴四边形EBGC是平行四边形.
∴BG∥EC. ∴
在
即异面直线与CE所成角的余弦值是
(2)过 作 交CE的延长线于H.连结AH. 底面ABCD如图所示.
由于∠AHE=∠B=90°,∠AEH=∠CEB,则△AHE∽△CBE
设点A到平面的距离为,则由三棱锥体积公式可得:,即。所以,
即点A到平面的距离为。
9、[证明]在三棱柱中,侧棱底面,,或它的补角即为异面直线与所成角,…………………………2分
由,,以及正弦定理得,即,…………4分
又,,…………6分
………………8分
所以异面直线与所成角的为.…………………… 10分
三棱柱的体积为. …………12分
10、证明:在中,因为分别为的中点,所以……………………………………………………………………………2分
又因为,所以由平行公理和等量代换知,,
所以四边形是平行四边形……………………………………………………4分
所以…………………………………………………………………………6分
又因为平面,所以平面…………………………………8分
11、
( http: / / www.21cnjy.com )
12、解:(1)证明:,,
又中, ,点为线段的中点,
(2),又,,
连结,可得是与平面所成角,又与平面所成角的大小为,, 在中,,
.分
13、解: (1)由已知得, ……………………2分
所以 ,体积 ……………………5分
(2)取中点,连接,则,
所以就 是异面直线与所成的角. ……………………8分
由已知,,
. ……………………10分
在中,,
所以,. ……………………12分
14、解:因为,,所以平面,所以.又.所以平面.故.--------6分
在中,,所以.----8分
又在中,,所以.---10分
又因为平面,所以.----------12分
15、解:(1)如图,连接交于点,则为线段中点,
在正方形中,对角线 (2分)
在中,,
,平面 (2分)
(2分)
(2)边长为3米 (2分)
棱锥的高 (2分)
立方米 (2分)
答:需要立方米填充材料.
①
②
A
B
C
A1
B1
C1
A
B
D
C
H
P
第19题图
立体几何
一、填空题
1、(宝山区2016届高三上学期期末)等腰直角三角形的直角边长为1,则绕斜边旋转一周所形成的几何体的体积为
2、(崇明县2016届高三上学期期末)已知圆锥的母线长为5cm,侧面积为15cm2,则此圆锥的体积是____________ cm3 .
3、(虹口区2016届高三上学期期末)如图所示,半径的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于__________
4、(黄浦区2016届高三上学期期末)若将两个半径为的铁球熔化后铸成一个球,则该球的半径为 .
5、(嘉定区2016届高三上学期期末)在正方体中,为棱的中点,则异面直线与所成的角的大小为__________________(结果用反三角函数值表示).
6、(嘉定区2016届高三上学期期末)在若圆锥的底面周长为,侧面积也为,则该圆锥的体积为______________.
7、(静安区2016届高三上学期期末)已 ( http: / / www.21cnjy.com )知球的半径为24cm,一个圆锥的高等于这个球的直径,而且球的表面积等于圆锥的表面积,则这个圆锥的体积是 cm3.
8、(闵行区2016届高三上学期期末)若一圆锥的底面半径为,体积是,则该圆锥的侧面积等于 .
9、(浦东新区2016届高三上学期期末)如图,已知正方体,,为棱的中点,则与平面所成的角为 (结果用反三角表示)
10、(普陀区2016届高三上学期期末)若正六棱柱的底面边长为10,侧面积为180,则这个棱柱的体积为_________
11、(青浦区2016届高三上学期期末)平面直角坐标系中,方程的曲线围成的封闭图形绕轴旋转一周所形成的几何体的体积为
12、(松江区2016届高三上学期期末)若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为、则有 ▲
13、(徐汇区2016届高三上学期期末)已知四面体的外接球球心在棱上,,,则、两点在四面体的外接球上的球面距离是________________.
14、(闸北区2016届高三上学期期末)一 ( http: / / www.21cnjy.com )个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是
填空题参考答案:
1、 2、12 3、 4、 5、
6、 7、 12288 8、 9、.(,)
10、450 11、 12、 13、 14、
二、选择题
1、(宝山区2016届高三上学期期末)若是异面直线,则下列命题中的假命题为--------- ( )
(A)过直线可以作一个平面并且只可以作一个平面与直线平行;
(B)过直线至多可以作一个平面与直线垂直;
(C)唯一存在一个平面与直线等距;
(D)可能存在平面与直线都垂直。
2、(嘉定区2016届高三上学期期末)下列四个命题:
①任意两条直线都可以确定一个平面;
②若两个平面有个不同的公共点,则这两个平面重合;
③直线,,,若与共面,与共面,则与共面;
④若直线上有一点在平面外,则在平面外.
其中错误命题的个数是( )
A. B. C. D.
3、(静安区2016届高三上学期期末)下列四个命题中,真命题是 ( )
A.和两条异面直线都相交的两条直线是异面直线;
B.和两条异面直线都垂直的直线是异面直线的公垂线;
C.和两条异面直线都相交于不同点的两条直线是异面直线;
D.若a、b是异面直线, b、c是异面直线,则a、c是异面直线.
4、(普陀区2016届高三上学期期末)如图,在四面体中,AB⊥BD,CD⊥DB,若与所成的角的大小为,则二面角C-BD-A的大小为( )
A. 或
B. 或
C. 或
D. 或
5、(徐汇区2016届高三上学期期末)在正方体中,、分别是棱、的中点,、分别是线段与上的点,则与平面平行的直线有
0条
1条
2条
无数条
6、(杨浦区2016届高三上学期期末)对于两个平面和两条直线, 下列命题中真命题是 ( )
A.若, , 则
B.若, , 则
C. 若,,,则
D. 若,,,则
7、(闸北区2016届高三上学期期末)已知是两条不同直线,是两个不同平面,给出下列四个命题:
① 若垂直于同一平面,则与平行;
② 若平行于同一平面,则与平行;
③ 若不平行,则在内不存在与平行的直线;
④ 若不平行,则与不可能垂直于同一平面
其中真命题的个数为( )
A. 4 B. 3 C. 2 D. 1
选择题参考答案:
1、D 2、C 3、C 4、C 5、D 6、D 7、D
三、解答题
1、(宝山区2016届高三上学期期末)在三棱锥中,已知PA,PB,PC两两垂直,PB=5,PC=6,三棱锥的体积为20,Q是BC的中点,求异面直线PB,AQ所成角的大小(结果用反三角函数值表示)。
( http: / / www.21cnjy.com )
2、(崇明县2016届高三上学期期末)如图,四棱锥S ABCD中,底面 ABCD 为正方形,SA ⊥平面 ABCD,AB=3,SA=4
(1)求异面直线SC 与AD 所成角;
(2)求点B 到平面SCD 的距离.
( http: / / www.21cnjy.com )
3、(奉贤区2016届高三上学期期末)如图,已知四边形是矩形,,,平面,且,
的中点,求异面直线与所成角的大小.(用反三角表示)
4、(虹口区2016届高三上学期期末)如图,在正三棱柱 中,已知它的底面边长为10,
高为20 .
求正三棱柱的表面积与体积;
若分别是的中点,求异面直线所
成角的大小(结果用反三角函数表示).
5、(黄浦区2016届高三上学期期末) 已知三棱柱的底面为直角三角形,两条直角边和的长分别为4和3,侧棱的长为10.
(1)若侧棱垂直于底面,求该三棱柱的表面积.
(2)若侧棱与底面所成的角为,求该三棱柱的体积.
6、(嘉定区2016届高三上学期期末)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为的正方形,高为,内有深的溶液.现将此容器倾斜一定角度(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(1)要使倾斜后容器内的溶液不会溢出,角的最大值是多少;
(2)现需要倒出不少于的溶液,当时,能实现要求吗?请说明理由.
7、(金山区2016届高三上学期期末)在直三棱柱中,,,且异面直线与所成的角等于,设.
(1) 求的值;
(2) 求三棱锥的体积.
8、(静安区2016届高三上学期期末) 如图,在棱长为1的正方体中,E为AB的中点. 求:
(1)异面直线BD1与CE所成角的余弦值;
(2)点A到平面的距离.
9、(闵行区2016届高三上学期期末)
如图,三棱柱中,侧棱底面,,,,为棱中点,证明异面直线与所成角为,并求三棱柱的体积.
( http: / / www.21cnjy.com )
10、(浦东新区2016届高三上学期期末)
已知交与点,,分别为的中点.
求证:平面.
11、(普陀区2016届高三上学期期末)某种“笼其”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为,高为,圆锥的母线长为.
(1)求这种“笼其”的体积(结果精确到0.1);
(2)现要使用一种纱网材料制作50个“笼其”,该材料的造价为每平方米8元,共需多少元?
( http: / / www.21cnjy.com )
12、(青浦区2016届高三上学期期末)
如图所示,在四棱锥中,,∥且,,点为线段的中点,若,与平面所成角的大小为.
(1)证明:平面;
(2)求四棱锥的体积.
13、(松江区2016届高三上学期期末)
如图,在三棱锥中,平面,,,,分别是的中点.
(1)求三棱锥的体积;
(2)若异面直线与所成的角为,求的值.
14、(徐汇区2016届高三上学期期末)
在三棱锥中,且 .
求证并求三棱锥的体积.
15、(杨浦区2016届高三上学期期末) ( http: / / www.21cnjy.com )如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充。已知金字塔的每一条棱和边都相等
(1) 求证:直线垂直于直线.
若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
解答题参考答案
1、解:,所以,-------------------3分
取PC的中点为D,连结AD,DQ,
则为异面直线PB,AQ所成的角,--------------------------------5分
,,------------------------------------7分
因为,所以----------------------9分
所以
异面直线PB,AQ所成的角为。-----------------------12分
2、
( http: / / www.21cnjy.com )
3、取的中点,连接、
、是中点,是的中位线
∥
(或者其补角)为异面直线与所成角 3分
在中, 5分
6分
,, 7分
由余弦定理可知
10分
11分
异面直线与所成角的大小. 12分
4、解:(1) ……(3分)
……(6分)
(2)连结则又
故等于异面直线所成角. ……(8分)
易得,故
于是异面直线所成角的大小为……(12分)
5、[解](1)因为侧棱底面,所以三棱柱的高等于侧棱的长,
而底面三角形的面积,(2分)
周长,(4分)
于是三棱柱的表面积.(6分)
(2)如图,过作平面的垂线,垂足为,为三棱柱的高.(8分)
因为侧棱与底面所成的角为,所以,可计算得.(9分)
又底面三角形的面积,故三棱柱的体积.(12分)
6、(1)如图③,当倾斜至上液面经过点时,容器内溶液恰好不会溢出,
此时最大. …………………………………………………………………(2分)
解法一:此时,梯形的面积等于(), ………………(3分)
因为,所以,,
即,解得,. ………………(5分)
所以,要使倾斜后容器内的溶液不会溢出,的最大值是. ……………(6分)
解法二:此时,△的面积等于图①中没有液体部分的面积,
即(), ……………………………………………………(3分)
因为,所以,即,
解得,. …………………………………………(5分)
所以,要使倾斜后容器内的溶液不会溢出,的最大值是. …………(6分)
(2)如图④,当时,设上液面为,因为,
所以点在线段上, ………………………………………………………(1分)
此时,,
(), ………………………………………(3分)
剩余溶液的体积为(), …………………………(4分)
由题意,原来溶液的体积为,
因为,所以倒出的溶液不满. …………(5分)
所以,要倒出不少于的溶液,当时,不能实现要求.……(6分)
7、解(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,
即∠A1BC =60,…………………………………………………………………………2分
又AA1⊥平面ABC,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,…………4分
由,,
∴;……………………………………………6分
(2)连接B1C,则三棱锥B1–A1BC的体积等于三棱锥C–A1B1B的体积,
即:,………………………………………………………………9分
△的面积,……………………………………………………………11分
又平面,
所以,所以.………………………………14分
8、解(1)延长DC至G,使CG= DC,连结BG、
,∴四边形EBGC是平行四边形.
∴BG∥EC. ∴
在
即异面直线与CE所成角的余弦值是
(2)过 作 交CE的延长线于H.连结AH. 底面ABCD如图所示.
由于∠AHE=∠B=90°,∠AEH=∠CEB,则△AHE∽△CBE
设点A到平面的距离为,则由三棱锥体积公式可得:,即。所以,
即点A到平面的距离为。
9、[证明]在三棱柱中,侧棱底面,,或它的补角即为异面直线与所成角,…………………………2分
由,,以及正弦定理得,即,…………4分
又,,…………6分
………………8分
所以异面直线与所成角的为.…………………… 10分
三棱柱的体积为. …………12分
10、证明:在中,因为分别为的中点,所以……………………………………………………………………………2分
又因为,所以由平行公理和等量代换知,,
所以四边形是平行四边形……………………………………………………4分
所以…………………………………………………………………………6分
又因为平面,所以平面…………………………………8分
11、
( http: / / www.21cnjy.com )
12、解:(1)证明:,,
又中, ,点为线段的中点,
(2),又,,
连结,可得是与平面所成角,又与平面所成角的大小为,, 在中,,
.分
13、解: (1)由已知得, ……………………2分
所以 ,体积 ……………………5分
(2)取中点,连接,则,
所以就 是异面直线与所成的角. ……………………8分
由已知,,
. ……………………10分
在中,,
所以,. ……………………12分
14、解:因为,,所以平面,所以.又.所以平面.故.--------6分
在中,,所以.----8分
又在中,,所以.---10分
又因为平面,所以.----------12分
15、解:(1)如图,连接交于点,则为线段中点,
在正方形中,对角线 (2分)
在中,,
,平面 (2分)
(2分)
(2)边长为3米 (2分)
棱锥的高 (2分)
立方米 (2分)
答:需要立方米填充材料.
①
②
A
B
C
A1
B1
C1
A
B
D
C
H
P
第19题图
同课章节目录
