北师大版八年级数学上册试题 第3章 位置与坐标 单元培优卷(含解析)
文档属性
| 名称 | 北师大版八年级数学上册试题 第3章 位置与坐标 单元培优卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 841.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 12:27:10 | ||
图片预览


文档简介
第3章《位置与坐标》(单元培优卷)
一、单选题(本大题共10小题,每小题3分,共30分)
1.已知点A(1,2a-1),B(-a,a-3),若线段AB//x轴,则三角形AOB的面积为( )
A.21 B.28 C.14 D.10.5
2.已知点P(x,y)到x轴的距离为2,到y轴的距离为3,且x+y>0,xy<0,则点P的坐标为( )
A.(﹣2,3) B.(2,3) C.(3,﹣2) D.(3,2)
3.若点到两坐标轴的距离相等,则点的坐标( )
A. B. C.或 D.或
4.对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(﹣a,b),如f(1,2)=(﹣1,2);g(a,b)=(b,a),如g(1,2)=(2,1),据此得g[f(5,﹣9)]=( )
A.(5,﹣9) B.(﹣5,﹣9) C.(﹣9,﹣5) D.(﹣9,5)
5.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
6.已知点A(3a,2b)在x轴上方,在y轴左侧,则点A到x轴、y的距离分别为( )
A.3a,-2b B.-3a,2b C.2b,-3a D.-2b,3a
7.如图,在平面直角坐标系中,的顶点坐标分别为,,,,则的值为( )
A.8 B.9 C.12 D.11
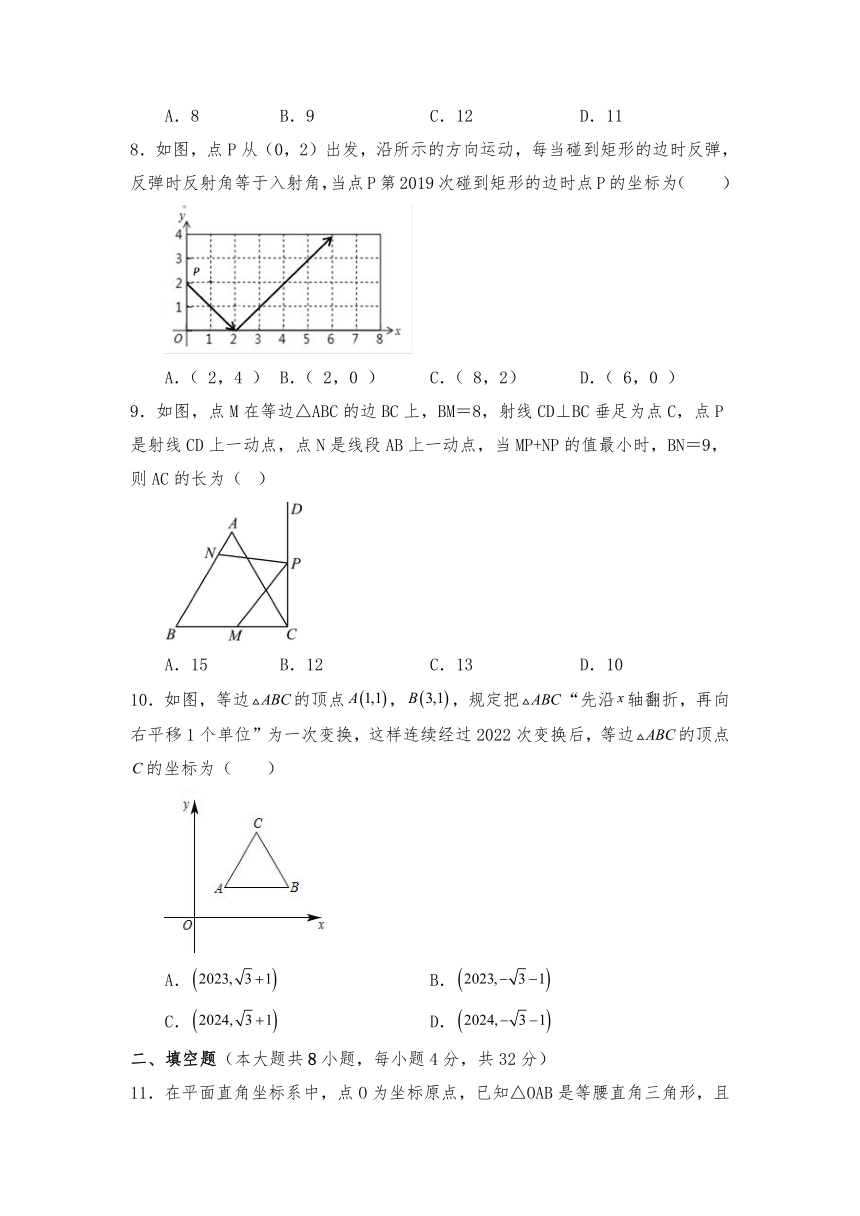
8.如图,点P从(0,2)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2019次碰到矩形的边时点P的坐标为( )
A.( 2,4 ) B.( 2,0 ) C.( 8,2) D.( 6,0 )
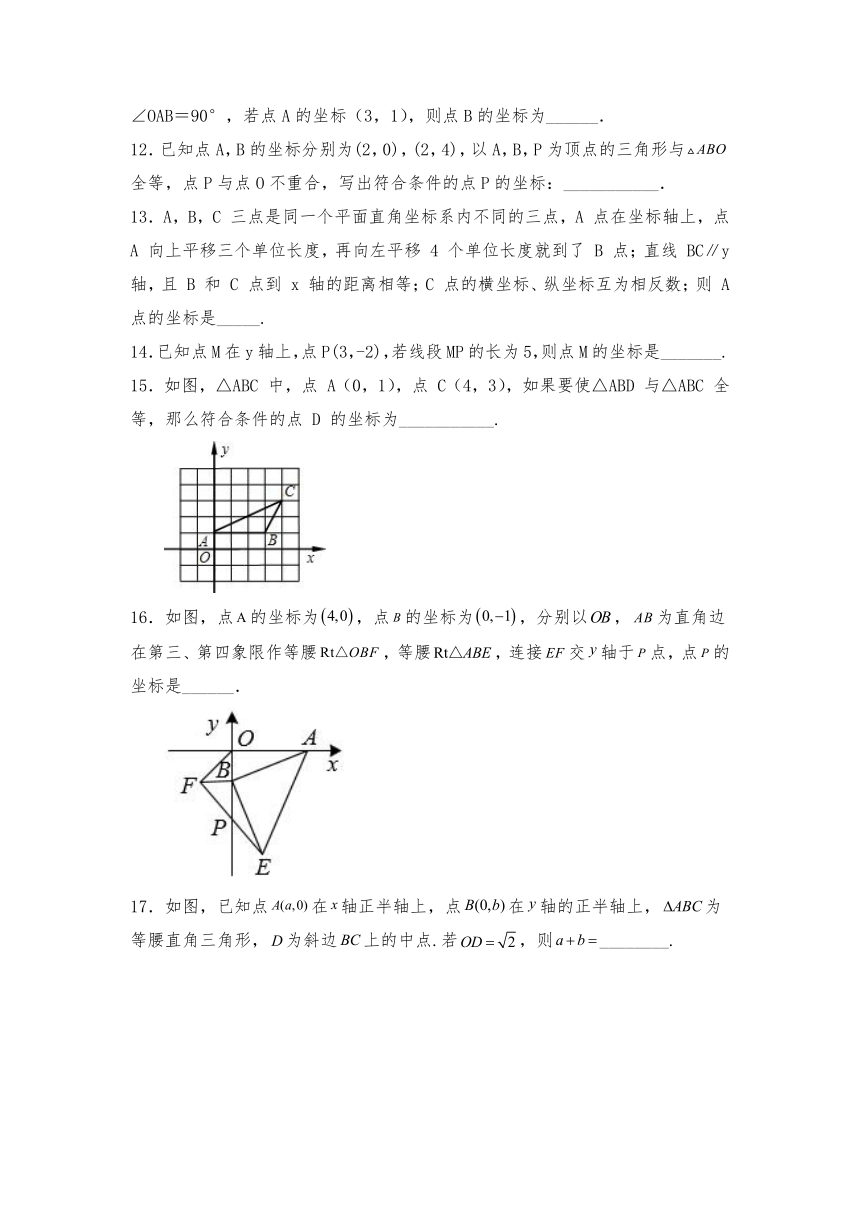
9.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为( )
A.15 B.12 C.13 D.10
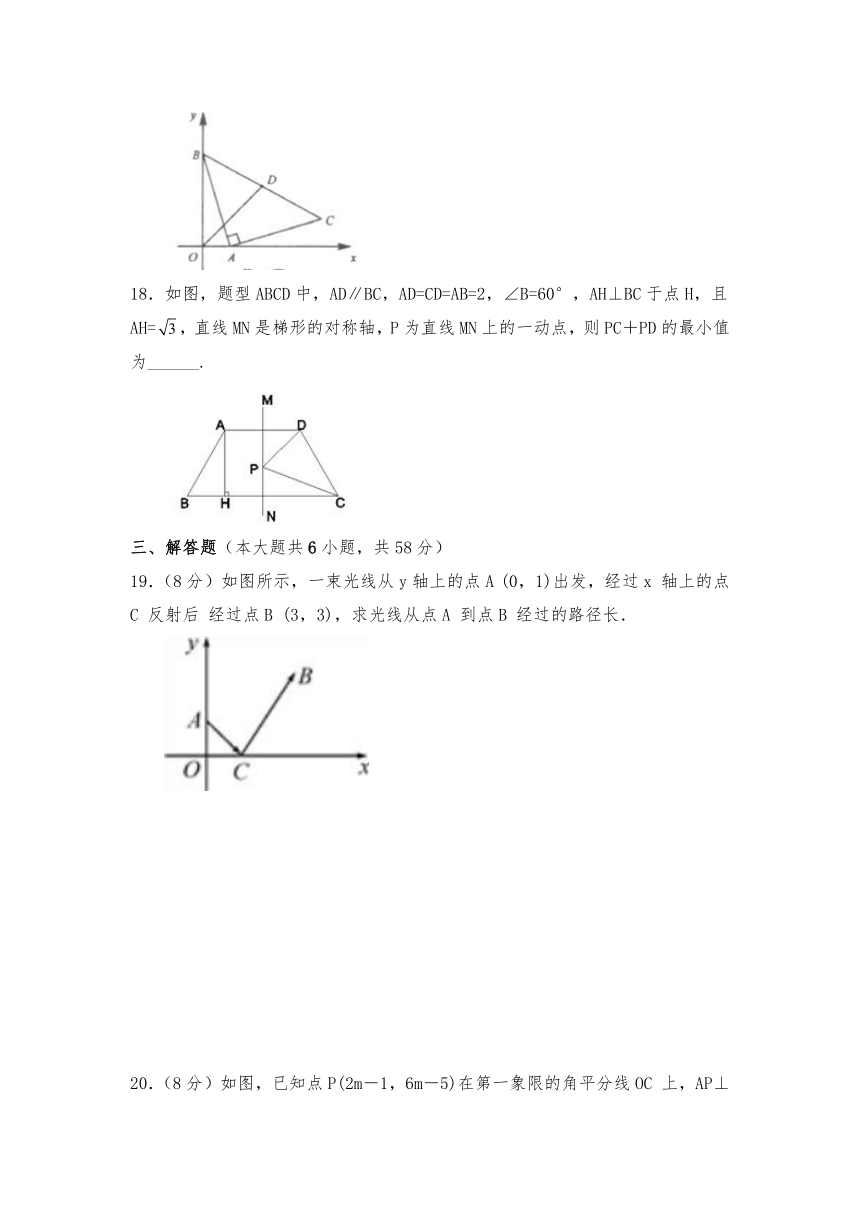
10.如图,等边的顶点,,规定把“先沿轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边的顶点的坐标为( )
A. B.
C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.在平面直角坐标系中,点O为坐标原点,已知△OAB是等腰直角三角形,且∠OAB=90°,若点A的坐标(3,1),则点B的坐标为______.
12.已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与全等,点P与点O不重合,写出符合条件的点P的坐标:___________.
13.A,B,C 三点是同一个平面直角坐标系内不同的三点,A 点在坐标轴上,点 A 向上平移三个单位长度,再向左平移 4 个单位长度就到了 B 点;直线 BC∥y 轴,且 B 和 C 点到 x 轴的距离相等;C 点的横坐标、纵坐标互为相反数;则 A 点的坐标是_____.
14.已知点M在y轴上,点P(3,-2),若线段MP的长为5,则点M的坐标是_______.
15.如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为___________.
16.如图,点的坐标为,点的坐标为,分别以,为直角边在第三、第四象限作等腰,等腰,连接交轴于点,点的坐标是______.
17.如图,已知点在轴正半轴上,点在轴的正半轴上,为等腰直角三角形,为斜边上的中点.若,则________.
18.如图,题型ABCD中,AD∥BC,AD=CD=AB=2,∠B=60°,AH⊥BC于点H,且AH=,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
三、解答题(本大题共6小题,共58分)
19.(8分)如图所示,一束光线从y轴上的点A (0,1)出发,经过x 轴上的点C 反射后 经过点B (3,3),求光线从点A 到点B 经过的路径长.
20.(8分)如图,已知点P(2m-1,6m-5)在第一象限的角平分线OC 上,AP⊥BP,点A在x轴上,点 B在y轴正半轴上.
(1)求点P 的坐标;
(2)当∠APB绕点P旋转时,OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
21.(10分)在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1) 直接写出点B和点C的坐标.
(2) 当点P运动时,用含t的式子表示线段AP的长,
(3) 点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使,若存在,请求出t值,若不存在,请说明理由.
22.(10分)如图,的顶点A,B分别在x轴,y轴上,;
(1)若,且点B(0,2),C(-2,-1),
①点C关于y轴对称点的坐标为______;
②求点A的坐标;
(2)若点B与原点重合,时,存在第三象限的点E和y轴上的点F,使,且A(3,0),C(0,m),F(0,n),线段EF的长度为,求AE的长.
23.(10分)如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式,
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
24.(12分)已知,△ABC满足BC=AB,∠ABC=90°,A点在x轴的负半轴上,直角顶点B在y轴上,点C在x轴上方.
(1)如图1所示,若A的坐标是(-3,0),点B与原点重合,则点C的坐标是_________;
(2)如图2,过点C作CD⊥y轴于D,请判断线段OA、OD、CD之间的数量关系并说明理由;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于点F,问CF与AE有怎样的数量关系?并说明理由.
参考答案
一、单选题
1.D
【分析】根据线段AB∥x轴求得a的值后即可确定点A和点B的坐标,从而求得线段AB的长,利用三角形的面积公式求得三角形的面积即可.
解:∵AB∥x轴,∴2a+1=a-3.解得a=-4.
∴A(1,-7),B(4,-7).
∴AB=3.
过点O作OC⊥AB交BA的延长线于点C,
则OC=7.
∴△ABC的面积为:.
故答案为:D.
2.C
【分析】由点P(x,y)到X轴距离为2,到Y轴距离为3,可得x,y的可能的值,由x+y>0,xy<0,可得两数异号,且正数的绝对值较大;根据前面得到的结论即可判断点P的坐标.
解:∵点P(x,y)到x轴距离为2,到y轴距离为3,
∴|x|=3,|y|=2,
∴x=±3,y=±2;
∵x+y>0,xy<0,
∴x=3,y=﹣2,
∴P的坐标为(3,﹣2),
故选:C.
3.D
【分析】根据点到两坐标轴的距离相等列出绝对值方程,然后求解即可.
解:点到两坐标轴的距离相等,
,
或,
解得或,
点的坐标为或;
故选:.
4.C
【分析】根据f,g两种变换的定义自内而外进行解答即可.
解:由题意得,f(5,﹣9)]=(﹣5,﹣9),
∴g[f(5,﹣9)]=g(﹣5,﹣9)=(﹣9,﹣5),
故选:C.
5.B
【分析】过点C作CD⊥x轴于D,由“AAS”可证△AOB≌△BDC,可得AO=BD=2,BO=CD=n=a,即可求解.
解:如图,过点C作CD⊥x轴于D,
∵点A(0,2),
∴AO=2,
∵△ABC是等腰直角三角形,且AB=BC,
∴∠ABC=90°=∠AOB=∠BDC,
∴∠ABO+∠CBD=90°
∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在△AOB和△BDC中,
,
∴△AOB≌△BDC(AAS),
∴AO=BD=2,BO=CD=n=a,
∴0<a<1,
∵OD=OB+BD=2+a=m,
∴2<m<3,
故选:B.
6.C
【分析】应先判断出点A的横纵坐标的符号,进而判断点A到x轴、y轴的距离.
解:∵点A(3a,2b)在x轴上方,
∴点A的纵坐标大于0,得到2b>0,
∴点A到x轴的距离是2b;
∵点A(3a,2b)在y轴的左边,
∴点A的横坐标小于0,即3a<0,
∴点A到y轴的距离是-3a;
故答案为C.
7.C
【分析】利用中点坐标公式,构建方程求出a,b的值即可.
解:如图,连接AC、BD交于点F,
∵四边形ABCD是平行四边形,
∴AF=CF,BF=DF,
∵,,,,
∴,
∴,
∴.
故选:C.
8.C
【分析】动点的反弹与光的反射入射是一个道理,根据反射角与入射角的定义可以在格点中作出图形,可以发现,在经过6次反射后,动点回到起始的位置,将2019除以6得到336,且余数为3,说明点P第2019次碰到矩形的边时为第337个循环组的第3次反弹,因此点P的坐标为(8,2).
解:如图,根据反射角与入射角的定义作出图形,
第6次反弹时回到出发点,每6次碰到矩形的边为一个循环组依次循环,
∵2019÷6=336……3,
∴点P第2019次碰到矩形的边时是第336个循环组的第3次碰边,坐标为(8,2).
故选C.
9.C
【分析】由AC=BC,,作点M关于直线CD的对称点G,过G作于点,交CD于P,则此时MP+PN的值最小,再由直角三角形即可求出答案
解:如图:
是等边三角形
,
作点M关于直线CD的对称点G,过G作于点 ,交CD于P,
为最小值
,
故答案选C
10.C
【分析】先利用等边三角形的性质求得点C的坐标,然后根据轴对称变换和轴对称变换的性质求得第一次变换,第二次变换,第三次变换后点C的坐标,按此找出规律即可求解 .
解:如图所示,过点作,
∵△ABC是等边三角形,,,
∴,,轴,D的坐标为(2,1),
∴
∴点C到轴的距离为:,点的横坐标为,
∴,
由题意得,
第一次变换后点的坐标为,即;
第二次变换后点的坐标为,即;
第三次变换后点的坐标为,即;
……
由此可以发现点的横坐标总是比次数大,而纵坐标,当奇次变换时是,偶次变换时是,故连续经过2022次变换后,等边的顶点的坐标为,
故选:
二、填空题
11.(2,4)或(4,﹣2)
【分析】分两种情况讨论:当点B在第一象限时,过A作AC⊥x轴于C,过B作BD⊥AC于D;当点B'在第四象限时,过A作AE⊥y轴于E,过B'作B'F⊥AE于F,分别依据全等三角形的对应边相等,即可得到点B的坐标.
解:如图,当点B在第一象限时,过A作AC⊥x轴于C,过B作BD⊥AC于D,则AC=1,OC=3,
易得△ABD≌△OAC(AAS),
∴AC=BD=1,AD=OC=3,
∴B(2,4);
当点B'在第四象限时,过A作AE⊥y轴于E,过B'作B'F⊥AE于F,则OE=1,AE=3,
易得△AOE≌△B'AF(AAS),
∴AF=OE=1,B'F=AE=3,
∴B'(4,-2),
故答案为(2,4)或(4,-2).
12.或或
【分析】分和两种情况,再分别利用全等三角形的性质求解即可得.
解:设点P的坐标为,
,
,
由题意,分以下两种情况:
(1)如图1,当时,
,
轴,
,
又,
,
解得或,
则此时点P的坐标为或;
(2)如图2,当时,
,
点P在x轴上,且,
则此时点P的坐标为;
综上,符合条件的点P的坐标为或或,
故答案为:或或.
13.(7,0)或(0,-7)
【分析】设C点坐标为(a,-a),根据题意和平移逆向推出B、A的坐标,然后讨论A点在哪个坐标轴上, 即可完成解答.
解:设C点坐标为(a,-a),则B的坐标为(a,a),A点坐标为(a+4,a-3);
当A在x轴上,即a-3=0,即a=3,则坐标为(7,0)
当A在y轴上,即a+4=0,即a=-4,则坐标为(0,-7)
综上,本题答案为:(7,0)或(0,-7)
14.(0,2)或(0,-6)
【分析】如图,以点P为圆心,5为半径画弧,交y轴于M1、M2两点,过P点作y轴的垂线,垂足为N,在Rt△PM1N和Rt△PM2N中,由勾股定理得M1N=M2N=4,再由N(0,-2)即可得点M的坐标.
解:如图,以点P为圆心,5为半径画弧,交y轴于M1、M2两点,过P点作y轴的垂线,垂足为N.
∴在Rt△PM1N和Rt△PM2N中,M1N=M2N==4,
又∵N(0,-2),
∴M(0,2)或(0,-6).
故答案为:(0,2)或(0,-6).
15.或或(-1,3)
【分析】因为与有一条公共边,故应该分情况讨论D点的坐标.
解:因为与的一条边重合
当点在的下方时,满足条件的坐标有和;
当点在的上方时,满足条件的坐标是.
故满足条件的为或或(-1,3)
16.
【分析】作轴于,求出,证,得BN=AO,再由,证,推出=2,由点的坐标为即可得出点的坐标为.
解:如图,作轴于,
,
,,
,
在和中,
,
,OA=BN
,
在和中,
,
,
,
又因为点的坐标为,
,
,
又∵点的坐标为,
∴点的坐标为.
故答案为:.
17.2
【分析】根据等腰直角三角形的性质,可得AP与BC的关系,根据垂线的性质,可得答案
解:如图:作CP⊥x轴于点P,由余角的性质,得∠OBA=∠PAC,
在Rt△OBA和Rt△PAC中,
,
Rt△OBA≌Rt△PAC(AAS),
∴AP=OB=b,PC=OA=a.
由线段的和差,得OP=OA+AP=a+b,即C点坐标是(a+b,a),
由B(0,b),C(a+b,a),D是BC的中点,得D(,),
∴OD=
∴=,
∴a+b=2.
故答案为2.
18.
解:连接AC交直线MN于P点,P点即为所求.
∵直线MN为梯形ABCD的对称轴,
∴AP=DP,
∴当A、P、C三点位于一条直线时,PC+PD=AC,为最小值,
∵AD=DC=AB,AD∥BC,
∴∠DCB=∠B=60°,
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠DAC=∠DCA,
∴∠DAC=∠DCA=∠ACB
∵∠ACB+∠DCA=60°,
∴∠DAC=∠DCA=∠ACB=30°,
∴∠BAC=90°,
∵AB=2,∠B=60°
∴AC=tan60°×AB=×2=2.
∴PC+PD的最小值为2.
三、解答题
19.
解:如图,作点B关于x轴的对称点B′,连接AB′交x轴于点C,过点B′作B′D⊥y轴于点D.
因为点 A(0,1),点 B(3,3),所以 B′(3,-3),D(0,-3).
在 Rt△ADB′中, AD=1-(-3)=4,DB′=3,
所以 AB′2=AD2+DB′2=42+32=25,所以 AB′=5,
所以 AC+CB=5,
光线从 A 点到 B 点的路径长为 5.
20.
解:(1)由题意,得 2m-1=6m-5.解得 m=1,
∴点 P 的坐标为(1,1)
(2)作 PD⊥x 轴于点 D,PE⊥y 轴于点 E,
则△PAD≌△PBE,
∴AD=BE,
∴OA+OB=OD+AD+OB=OD+BE+OB=OD+OE=2,为定值,
故 OA+OB 的值不发生变化,其值为 2.
21.
解:(1)B(0,6),C(8,0),
(2)当点P在线段BA上时,
由A(8,6),B(0,6),C(8,0)可得:AB=8,AC=6
∵AP=AB-BP,BP=2t,
∴AP=8-2t(0≤t<4);
当点P在线段AC上时,
∴AP=点P走过的路程-AB=2t-8(4≤t≤7).
(3)存在两个符合条件的t值,
当点P在线段BA上时
∵,
∴,
解得:t=3,
当点P在线段AC上时,
∵ CD=8-2=6
∴,
解得:t=5,
综上所述:当t为3秒和5秒时.
22.
解:(1)①由关于y轴对称的点纵坐标不变、横坐标变为原来的相反数,则点C(-2,-1)关于y轴对称点的坐标为(2,-1);
故答案是(2,-1);
②设A点坐标为(a,0)
∵B(0,2),C(-2,-1),
∴BC=
∴AB=BC=
∴,解得a=3.
∴点A的坐标为(3,0).
(2)解:(2)作点F关于x轴的对称点H(0,-n),则AF=AH、OF=OH,过点H作HN⊥AC于点N,过点F作FM⊥AE于点M,
∵C(0,m),H(0,-n),m<0,n>0,
∴HC=OC-OH=-m-n,
∵EF=-m-n,
∴HC=EF,
∵∠AEF=∠ACO=30°,
∴∠FME=∠HNC,
∴△FEM≌△HCN(AAS),
∴FM=HN,EM=CN,
在Rt△AFM和Rt△AHN中,
AF=AH,FM=HN
∴Rt△AFM≌Rt△AHN(HL),
∴AM=AN,
∴EM+AM=CN+AN,
∴AE=AC,
∵∠ACO=30°,A(3,0),
∴OA=3,
∴AC=2OA=6,
∴AE=6.
23.
解:(1)由已知,
可得:a=2,b=3,c=4;
故答案为:a=2,b=3,c=4.
(2)∵S△ABO=×2×3=3,
S△APO=×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m,
即S四边形ABOP=3﹣m;
故答案为:S四边形ABOP=3﹣m.
(3)因为S△ABC=×4×3=6,
∵S四边形ABOP=S△ABC
∴3﹣m=6,
则m=﹣3,
所以存在点P(﹣3,)使S四边形ABOP=S△ABC.
故答案为:存在,P(﹣3,).
24.
解:(1)∵BC=AB,且A的坐标是( 3,0),
∴BC=BA=3,
∴点C的坐标为(0,3),
故答案为(0,3);
(2)OA=OD+CD;
∵CD⊥y轴,
∴∠ABO=∠DCB,
在△ABO和△BCD中,
∴BO=CD,OA=DB,
∵BD=OB+OD,
∴OA=CD+OD.
(3)AE=2CF,
如图3,延长CF,AB相交于G,
∵x轴恰好平分∠BAC,
∴∠CAF=∠GAF,
∵CF⊥x轴,
∴∠AFE=∠AFG=90 ,
在△AFC和△AFG中,
∵
∴CF=GF,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
∵
∴AE=CG,
∴AE=CF+GF=2CF
一、单选题(本大题共10小题,每小题3分,共30分)
1.已知点A(1,2a-1),B(-a,a-3),若线段AB//x轴,则三角形AOB的面积为( )
A.21 B.28 C.14 D.10.5
2.已知点P(x,y)到x轴的距离为2,到y轴的距离为3,且x+y>0,xy<0,则点P的坐标为( )
A.(﹣2,3) B.(2,3) C.(3,﹣2) D.(3,2)
3.若点到两坐标轴的距离相等,则点的坐标( )
A. B. C.或 D.或
4.对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(﹣a,b),如f(1,2)=(﹣1,2);g(a,b)=(b,a),如g(1,2)=(2,1),据此得g[f(5,﹣9)]=( )
A.(5,﹣9) B.(﹣5,﹣9) C.(﹣9,﹣5) D.(﹣9,5)
5.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
6.已知点A(3a,2b)在x轴上方,在y轴左侧,则点A到x轴、y的距离分别为( )
A.3a,-2b B.-3a,2b C.2b,-3a D.-2b,3a
7.如图,在平面直角坐标系中,的顶点坐标分别为,,,,则的值为( )
A.8 B.9 C.12 D.11
8.如图,点P从(0,2)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2019次碰到矩形的边时点P的坐标为( )
A.( 2,4 ) B.( 2,0 ) C.( 8,2) D.( 6,0 )
9.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为( )
A.15 B.12 C.13 D.10
10.如图,等边的顶点,,规定把“先沿轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边的顶点的坐标为( )
A. B.
C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.在平面直角坐标系中,点O为坐标原点,已知△OAB是等腰直角三角形,且∠OAB=90°,若点A的坐标(3,1),则点B的坐标为______.
12.已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与全等,点P与点O不重合,写出符合条件的点P的坐标:___________.
13.A,B,C 三点是同一个平面直角坐标系内不同的三点,A 点在坐标轴上,点 A 向上平移三个单位长度,再向左平移 4 个单位长度就到了 B 点;直线 BC∥y 轴,且 B 和 C 点到 x 轴的距离相等;C 点的横坐标、纵坐标互为相反数;则 A 点的坐标是_____.
14.已知点M在y轴上,点P(3,-2),若线段MP的长为5,则点M的坐标是_______.
15.如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为___________.
16.如图,点的坐标为,点的坐标为,分别以,为直角边在第三、第四象限作等腰,等腰,连接交轴于点,点的坐标是______.
17.如图,已知点在轴正半轴上,点在轴的正半轴上,为等腰直角三角形,为斜边上的中点.若,则________.
18.如图,题型ABCD中,AD∥BC,AD=CD=AB=2,∠B=60°,AH⊥BC于点H,且AH=,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
三、解答题(本大题共6小题,共58分)
19.(8分)如图所示,一束光线从y轴上的点A (0,1)出发,经过x 轴上的点C 反射后 经过点B (3,3),求光线从点A 到点B 经过的路径长.
20.(8分)如图,已知点P(2m-1,6m-5)在第一象限的角平分线OC 上,AP⊥BP,点A在x轴上,点 B在y轴正半轴上.
(1)求点P 的坐标;
(2)当∠APB绕点P旋转时,OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
21.(10分)在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1) 直接写出点B和点C的坐标.
(2) 当点P运动时,用含t的式子表示线段AP的长,
(3) 点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使,若存在,请求出t值,若不存在,请说明理由.
22.(10分)如图,的顶点A,B分别在x轴,y轴上,;
(1)若,且点B(0,2),C(-2,-1),
①点C关于y轴对称点的坐标为______;
②求点A的坐标;
(2)若点B与原点重合,时,存在第三象限的点E和y轴上的点F,使,且A(3,0),C(0,m),F(0,n),线段EF的长度为,求AE的长.
23.(10分)如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式,
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
24.(12分)已知,△ABC满足BC=AB,∠ABC=90°,A点在x轴的负半轴上,直角顶点B在y轴上,点C在x轴上方.
(1)如图1所示,若A的坐标是(-3,0),点B与原点重合,则点C的坐标是_________;
(2)如图2,过点C作CD⊥y轴于D,请判断线段OA、OD、CD之间的数量关系并说明理由;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于点F,问CF与AE有怎样的数量关系?并说明理由.
参考答案
一、单选题
1.D
【分析】根据线段AB∥x轴求得a的值后即可确定点A和点B的坐标,从而求得线段AB的长,利用三角形的面积公式求得三角形的面积即可.
解:∵AB∥x轴,∴2a+1=a-3.解得a=-4.
∴A(1,-7),B(4,-7).
∴AB=3.
过点O作OC⊥AB交BA的延长线于点C,
则OC=7.
∴△ABC的面积为:.
故答案为:D.
2.C
【分析】由点P(x,y)到X轴距离为2,到Y轴距离为3,可得x,y的可能的值,由x+y>0,xy<0,可得两数异号,且正数的绝对值较大;根据前面得到的结论即可判断点P的坐标.
解:∵点P(x,y)到x轴距离为2,到y轴距离为3,
∴|x|=3,|y|=2,
∴x=±3,y=±2;
∵x+y>0,xy<0,
∴x=3,y=﹣2,
∴P的坐标为(3,﹣2),
故选:C.
3.D
【分析】根据点到两坐标轴的距离相等列出绝对值方程,然后求解即可.
解:点到两坐标轴的距离相等,
,
或,
解得或,
点的坐标为或;
故选:.
4.C
【分析】根据f,g两种变换的定义自内而外进行解答即可.
解:由题意得,f(5,﹣9)]=(﹣5,﹣9),
∴g[f(5,﹣9)]=g(﹣5,﹣9)=(﹣9,﹣5),
故选:C.
5.B
【分析】过点C作CD⊥x轴于D,由“AAS”可证△AOB≌△BDC,可得AO=BD=2,BO=CD=n=a,即可求解.
解:如图,过点C作CD⊥x轴于D,
∵点A(0,2),
∴AO=2,
∵△ABC是等腰直角三角形,且AB=BC,
∴∠ABC=90°=∠AOB=∠BDC,
∴∠ABO+∠CBD=90°
∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在△AOB和△BDC中,
,
∴△AOB≌△BDC(AAS),
∴AO=BD=2,BO=CD=n=a,
∴0<a<1,
∵OD=OB+BD=2+a=m,
∴2<m<3,
故选:B.
6.C
【分析】应先判断出点A的横纵坐标的符号,进而判断点A到x轴、y轴的距离.
解:∵点A(3a,2b)在x轴上方,
∴点A的纵坐标大于0,得到2b>0,
∴点A到x轴的距离是2b;
∵点A(3a,2b)在y轴的左边,
∴点A的横坐标小于0,即3a<0,
∴点A到y轴的距离是-3a;
故答案为C.
7.C
【分析】利用中点坐标公式,构建方程求出a,b的值即可.
解:如图,连接AC、BD交于点F,
∵四边形ABCD是平行四边形,
∴AF=CF,BF=DF,
∵,,,,
∴,
∴,
∴.
故选:C.
8.C
【分析】动点的反弹与光的反射入射是一个道理,根据反射角与入射角的定义可以在格点中作出图形,可以发现,在经过6次反射后,动点回到起始的位置,将2019除以6得到336,且余数为3,说明点P第2019次碰到矩形的边时为第337个循环组的第3次反弹,因此点P的坐标为(8,2).
解:如图,根据反射角与入射角的定义作出图形,
第6次反弹时回到出发点,每6次碰到矩形的边为一个循环组依次循环,
∵2019÷6=336……3,
∴点P第2019次碰到矩形的边时是第336个循环组的第3次碰边,坐标为(8,2).
故选C.
9.C
【分析】由AC=BC,,作点M关于直线CD的对称点G,过G作于点,交CD于P,则此时MP+PN的值最小,再由直角三角形即可求出答案
解:如图:
是等边三角形
,
作点M关于直线CD的对称点G,过G作于点 ,交CD于P,
为最小值
,
故答案选C
10.C
【分析】先利用等边三角形的性质求得点C的坐标,然后根据轴对称变换和轴对称变换的性质求得第一次变换,第二次变换,第三次变换后点C的坐标,按此找出规律即可求解 .
解:如图所示,过点作,
∵△ABC是等边三角形,,,
∴,,轴,D的坐标为(2,1),
∴
∴点C到轴的距离为:,点的横坐标为,
∴,
由题意得,
第一次变换后点的坐标为,即;
第二次变换后点的坐标为,即;
第三次变换后点的坐标为,即;
……
由此可以发现点的横坐标总是比次数大,而纵坐标,当奇次变换时是,偶次变换时是,故连续经过2022次变换后,等边的顶点的坐标为,
故选:
二、填空题
11.(2,4)或(4,﹣2)
【分析】分两种情况讨论:当点B在第一象限时,过A作AC⊥x轴于C,过B作BD⊥AC于D;当点B'在第四象限时,过A作AE⊥y轴于E,过B'作B'F⊥AE于F,分别依据全等三角形的对应边相等,即可得到点B的坐标.
解:如图,当点B在第一象限时,过A作AC⊥x轴于C,过B作BD⊥AC于D,则AC=1,OC=3,
易得△ABD≌△OAC(AAS),
∴AC=BD=1,AD=OC=3,
∴B(2,4);
当点B'在第四象限时,过A作AE⊥y轴于E,过B'作B'F⊥AE于F,则OE=1,AE=3,
易得△AOE≌△B'AF(AAS),
∴AF=OE=1,B'F=AE=3,
∴B'(4,-2),
故答案为(2,4)或(4,-2).
12.或或
【分析】分和两种情况,再分别利用全等三角形的性质求解即可得.
解:设点P的坐标为,
,
,
由题意,分以下两种情况:
(1)如图1,当时,
,
轴,
,
又,
,
解得或,
则此时点P的坐标为或;
(2)如图2,当时,
,
点P在x轴上,且,
则此时点P的坐标为;
综上,符合条件的点P的坐标为或或,
故答案为:或或.
13.(7,0)或(0,-7)
【分析】设C点坐标为(a,-a),根据题意和平移逆向推出B、A的坐标,然后讨论A点在哪个坐标轴上, 即可完成解答.
解:设C点坐标为(a,-a),则B的坐标为(a,a),A点坐标为(a+4,a-3);
当A在x轴上,即a-3=0,即a=3,则坐标为(7,0)
当A在y轴上,即a+4=0,即a=-4,则坐标为(0,-7)
综上,本题答案为:(7,0)或(0,-7)
14.(0,2)或(0,-6)
【分析】如图,以点P为圆心,5为半径画弧,交y轴于M1、M2两点,过P点作y轴的垂线,垂足为N,在Rt△PM1N和Rt△PM2N中,由勾股定理得M1N=M2N=4,再由N(0,-2)即可得点M的坐标.
解:如图,以点P为圆心,5为半径画弧,交y轴于M1、M2两点,过P点作y轴的垂线,垂足为N.
∴在Rt△PM1N和Rt△PM2N中,M1N=M2N==4,
又∵N(0,-2),
∴M(0,2)或(0,-6).
故答案为:(0,2)或(0,-6).
15.或或(-1,3)
【分析】因为与有一条公共边,故应该分情况讨论D点的坐标.
解:因为与的一条边重合
当点在的下方时,满足条件的坐标有和;
当点在的上方时,满足条件的坐标是.
故满足条件的为或或(-1,3)
16.
【分析】作轴于,求出,证,得BN=AO,再由,证,推出=2,由点的坐标为即可得出点的坐标为.
解:如图,作轴于,
,
,,
,
在和中,
,
,OA=BN
,
在和中,
,
,
,
又因为点的坐标为,
,
,
又∵点的坐标为,
∴点的坐标为.
故答案为:.
17.2
【分析】根据等腰直角三角形的性质,可得AP与BC的关系,根据垂线的性质,可得答案
解:如图:作CP⊥x轴于点P,由余角的性质,得∠OBA=∠PAC,
在Rt△OBA和Rt△PAC中,
,
Rt△OBA≌Rt△PAC(AAS),
∴AP=OB=b,PC=OA=a.
由线段的和差,得OP=OA+AP=a+b,即C点坐标是(a+b,a),
由B(0,b),C(a+b,a),D是BC的中点,得D(,),
∴OD=
∴=,
∴a+b=2.
故答案为2.
18.
解:连接AC交直线MN于P点,P点即为所求.
∵直线MN为梯形ABCD的对称轴,
∴AP=DP,
∴当A、P、C三点位于一条直线时,PC+PD=AC,为最小值,
∵AD=DC=AB,AD∥BC,
∴∠DCB=∠B=60°,
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠DAC=∠DCA,
∴∠DAC=∠DCA=∠ACB
∵∠ACB+∠DCA=60°,
∴∠DAC=∠DCA=∠ACB=30°,
∴∠BAC=90°,
∵AB=2,∠B=60°
∴AC=tan60°×AB=×2=2.
∴PC+PD的最小值为2.
三、解答题
19.
解:如图,作点B关于x轴的对称点B′,连接AB′交x轴于点C,过点B′作B′D⊥y轴于点D.
因为点 A(0,1),点 B(3,3),所以 B′(3,-3),D(0,-3).
在 Rt△ADB′中, AD=1-(-3)=4,DB′=3,
所以 AB′2=AD2+DB′2=42+32=25,所以 AB′=5,
所以 AC+CB=5,
光线从 A 点到 B 点的路径长为 5.
20.
解:(1)由题意,得 2m-1=6m-5.解得 m=1,
∴点 P 的坐标为(1,1)
(2)作 PD⊥x 轴于点 D,PE⊥y 轴于点 E,
则△PAD≌△PBE,
∴AD=BE,
∴OA+OB=OD+AD+OB=OD+BE+OB=OD+OE=2,为定值,
故 OA+OB 的值不发生变化,其值为 2.
21.
解:(1)B(0,6),C(8,0),
(2)当点P在线段BA上时,
由A(8,6),B(0,6),C(8,0)可得:AB=8,AC=6
∵AP=AB-BP,BP=2t,
∴AP=8-2t(0≤t<4);
当点P在线段AC上时,
∴AP=点P走过的路程-AB=2t-8(4≤t≤7).
(3)存在两个符合条件的t值,
当点P在线段BA上时
∵,
∴,
解得:t=3,
当点P在线段AC上时,
∵ CD=8-2=6
∴,
解得:t=5,
综上所述:当t为3秒和5秒时.
22.
解:(1)①由关于y轴对称的点纵坐标不变、横坐标变为原来的相反数,则点C(-2,-1)关于y轴对称点的坐标为(2,-1);
故答案是(2,-1);
②设A点坐标为(a,0)
∵B(0,2),C(-2,-1),
∴BC=
∴AB=BC=
∴,解得a=3.
∴点A的坐标为(3,0).
(2)解:(2)作点F关于x轴的对称点H(0,-n),则AF=AH、OF=OH,过点H作HN⊥AC于点N,过点F作FM⊥AE于点M,
∵C(0,m),H(0,-n),m<0,n>0,
∴HC=OC-OH=-m-n,
∵EF=-m-n,
∴HC=EF,
∵∠AEF=∠ACO=30°,
∴∠FME=∠HNC,
∴△FEM≌△HCN(AAS),
∴FM=HN,EM=CN,
在Rt△AFM和Rt△AHN中,
AF=AH,FM=HN
∴Rt△AFM≌Rt△AHN(HL),
∴AM=AN,
∴EM+AM=CN+AN,
∴AE=AC,
∵∠ACO=30°,A(3,0),
∴OA=3,
∴AC=2OA=6,
∴AE=6.
23.
解:(1)由已知,
可得:a=2,b=3,c=4;
故答案为:a=2,b=3,c=4.
(2)∵S△ABO=×2×3=3,
S△APO=×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m,
即S四边形ABOP=3﹣m;
故答案为:S四边形ABOP=3﹣m.
(3)因为S△ABC=×4×3=6,
∵S四边形ABOP=S△ABC
∴3﹣m=6,
则m=﹣3,
所以存在点P(﹣3,)使S四边形ABOP=S△ABC.
故答案为:存在,P(﹣3,).
24.
解:(1)∵BC=AB,且A的坐标是( 3,0),
∴BC=BA=3,
∴点C的坐标为(0,3),
故答案为(0,3);
(2)OA=OD+CD;
∵CD⊥y轴,
∴∠ABO=∠DCB,
在△ABO和△BCD中,
∴BO=CD,OA=DB,
∵BD=OB+OD,
∴OA=CD+OD.
(3)AE=2CF,
如图3,延长CF,AB相交于G,
∵x轴恰好平分∠BAC,
∴∠CAF=∠GAF,
∵CF⊥x轴,
∴∠AFE=∠AFG=90 ,
在△AFC和△AFG中,
∵
∴CF=GF,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
∵
∴AE=CG,
∴AE=CF+GF=2CF
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
