沪科版九年级数学上册试题 21.5 反比例函数 同步练习 (含解析)
文档属性
| 名称 | 沪科版九年级数学上册试题 21.5 反比例函数 同步练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 615.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 14:34:18 | ||
图片预览




文档简介
21.5《反比例函数》
一、单选题
1.下列哪个点在反比例函数的图像上?( )
A. B. C. D.
2.若函数为反比例函数,则m的值是( )
A.1 B.0 C. D.
3.点,,都在反比例函数的图象上,则,,大小关系是( )
A. B. C. D.
4.反比例函数(为常数)的图象位于第一、三象限,则的取值范围是( )
A. B. C. D.
5.若函数的图象在第一、三象限内,则的取值范围是( )
A. B. C. D.
6.已知点,在反比例函数的图象上,且,则下列结论一定正确的是( )
A. B. C. D.
7.如图,已知点A为反比例函数的图象上一点,过点A作轴,垂足为B,若的面积为1,则k的值为( )
A.1 B. C.2 D.
8.对于反比例函数,下列说法正确的是( )
A.图象经过点 B.图象位于第一、三象限
C.当时,y随x的增大而增大 D.当时,y随x的增大而增大
9.一次函数和反比例函数在同一直角坐标系中的图像可能是( )
A. B. C. D.
10.下面的三个问题中都有两个变量:
①正方形的周长y与边长x;
②一种容积为的圆柱形量筒,量筒的底面积与量筒的高
③小赵骑行到公司上班,他骑行的平均速度y与骑行时间x;
其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是( )
A.②③ B.①② C.①③ D.①②③
二、填空题
11.已知点P(1,)在反比例函数y=(k≠0)的图像上,则k的值是 .
12.反比例函数图像经过、,且,那么的取值范围是 .
13.已知直线与双曲线的一个交点的坐标为,则它们的另一个交点的坐标是 .
14.在平面直角坐标系中,反比例函数的图像过点和点,则的值为 .
15.如图,两个反比例函数和(其中)在第一象限内的图象依次是和,设点P在上,轴于点C,交于点A,轴于点D,交于点B,则四边形的面积为 .
16.如图,点A、B是反比例函数y=(x>0)图象上的两点,且A、B两点的纵坐标分别为2和1,C在x轴上,AC=BC,∠ACB=90°,则k= .
17.某商店经营皮鞋,已知所获利润y(单位:元)与销售单价x(单价:元)之间的函数关系式为y=-x2+24x+2956,则获利最多为 元.
18.如图,一次函数与反比例函数的图像交于,两点.当时,的取值范围是 .
三、解答题
19.已知x,y满足下表.
x … 1 4 …
y … 4 1 …
(1)求y关于x的函数表达式:
(2)当时,求y的取值范围.
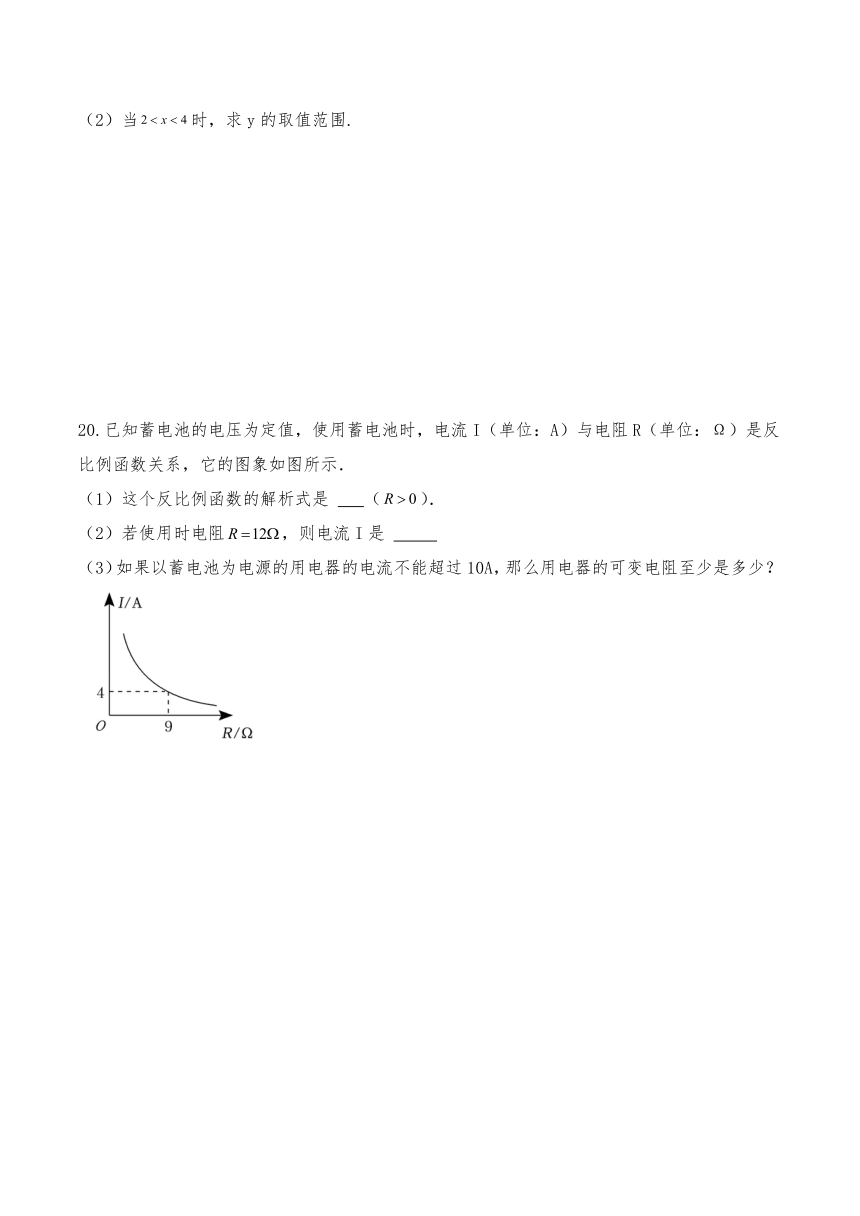
20.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)这个反比例函数的解析式是 ().
(2)若使用时电阻,则电流I是
(3)如果以蓄电池为电源的用电器的电流不能超过10A,那么用电器的可变电阻至少是多少?
21.已知反比例函数
(1)如果这个函数的图象经过点,求k的值;
(2)如果在这个函数图象所在的每个象限内,y的值随x的值增大而减小,求k的取值范围.
22.如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且的面积为,求点的坐标.
23.某商店以每件5元的价格购进一种文具,由试销知,该文具每天的销售量m(件)与单价x(元)之间满足一次函数关系.
(1)写出商店每天销售这种文具的利润y(元) 与单价x(元) 之间的函数关系式?
(2)商店要想每天获得利润21元,单价应定为多少元?
(3) 商店要想每天获得最大利润,单价应定为多少元?最大利润为多少?
24.如图,已知,是反比例函数的图象和一次函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出不等式的解集.
答案
一、单选题
1.D
【分析】根据反比例函数的图像上的点的横纵坐标乘积为4进行判断即可.
【详解】解:A.∵,∴不在反比例函数的图像上,故选项不符合题意;
B.∵,∴不在反比例函数的图像上,故选项不符合题意;
C.∵,∴不在反比例函数的图像上,故选项不符合题意;
D.∵,∴在反比例函数的图像上,故选项符合题意.
故选:D.
2.D
【分析】根据反比例函数的定义进行解答即可.
【详解】解:是反比例函数,
解得.
故选:D.
3.A
【分析】将点,,分别代入反比例函数,求得,,的值后,再来比较一下它们的大小.
【详解】解:∵点,,都在反比例函数的图象上,
∴,即,,即;,即,
∵,
∴;
故选:A.
4.B
【分析】根据反比例函数的性质可得m﹣2>0,进一步即可求出答案.
【详解】解:∵反比例函数(m为常数)的图象位于第一、三象限,
∴m﹣2>0,
解得:m>2.
故选:B.
5.A
【分析】根据反比例函数的性质得,然后解不等式即可.
【详解】解:根据题意得,
解得.
故选:A.
6.B
【分析】把点A和点B的坐标代入解析式,根据条件可判断出、的大小关系.
【详解】解:∵点,在反比例函数的图象上,
∴.
∵,
∴.
故选:B.
7.D
【分析】根据反比例函数的比例系数的几何意义可得,然后去绝对值即可得.
【详解】解:由反比例函数的图象可知,,
的面积为1,点为反比例函数的图象上一点,且轴,
,
解得或(舍去),
故选:D.
8.B
【分析】根据反比例函数的性质对各选项进行逐一分析即可.
【详解】解:,点不满足关系式,因此A选项不符合题意;
;
它的图象在第一、三象限,因此选项符合题意;
当时,它的图象在第三象限,随的增大而增小,因此C选项不符合题意;
当时,它的图象在第一象限,随的增大而增小,因此D选项不符合题意.
故选:B.
9.A
【分析】根据一次函数及反比例函数图像与性质逐项验证即可得到答案.
【详解】解:A、由一次函数图像可知,则,从而反比例函数图像在第一、三象限,该选项正确,符合题意;
B、由一次函数图像可知,则,从而反比例函数图像在第二、四象限,该选项错误,不符合题意;
C、由一次函数图像可知,则,从而反比例函数图像在第一、三象限,该选项错误,不符合题意;
D、由一次函数图像可知,则,从而反比例函数图像在第一、三象限,该选项错误,不符合题意;
故选:A.
10.A
【分析】分别求出三个问题中变量与变量之间的函数关系式即可得到答案.
【详解】解:①∵正方形的周长为,边长为,
∴,不符合题意;
②∵一种容积为的圆柱形量筒,量筒的底面积与量筒的高,
∴,即,符合题意;
③小赵骑行到公司上班,他骑行的平均速度为,骑行时间为,
∴,即,符合题意;
综上分析可知,变量y与变量x之间的函数关系可以用该图象表示的是②③,故B正确.
故选:B.
二、填空题
11..
【详解】试题分析:∵点P(1,)在反比例函数y=(k≠0)的图像上,
∴.
12.
【分析】直接利用反比例函数的增减性得出,进而求出答案.
【详解】解:∵反比例函数图像经过、,且,
∴每个象限内,随的增大而减小,
∴,
解得:,
∴的取值范围是.
故答案为:.
13.
【分析】根据反比例函数的图象是中心对称图形,则经过原点的直线的两个交点一定关于原点对称,即可求解.
【详解】解:∵直线与双曲线的一个交点的坐标为,且两图象的交点关于原点对称,
∴它们的另一个交点的坐标是.
故答案为:
14.
【分析】把点代入反比例函数解析式可求出反比例函数解析式,再把点代入计算即可.
【详解】解:∵反比例函数的图像过点,
∴,
∴反比例函数解析式为,
∵点在反比例函数,
∴,解得:,
故答案为:.
15.
【分析】根据反比例函数k值的意义,求出四边形的面积和,的面积即可得出答案.
【详解】解:∵,,
∴四边形的面积为:.
故答案为:.
16.6
【分析】过点A作AG⊥x轴于点G,过点B作BH⊥x轴于点H,易证△AGC≌CHB,根据全等三角形的性质,可得GC和CH的值,根据A、B的纵坐标,表示出横坐标,列方程求解即可.
【详解】过点A作AG⊥x轴于点G,过点B作BH⊥x轴于点H,如图所示,
则有∠AGC=∠CHB=90°,
∴∠GAC+∠GCA=90°,
∵∠ACB=90°,AC=BC,
∴∠ACG+∠HCB=90°,
∴∠GAC=∠HCB,
∴△AGC≌CHB(AAS),
∴AG=CH=2,GC=BH=1,∴GH=3
∵A、B在反比例函数的图象上,
∴,B(k,1),
∴,
∴k=6,
故答案为:6.
17.3100
【分析】根据抛物线的开口方向和顶点坐标的纵坐标公式即可求出结论.
【详解】解:∵a=-1,
∴y有最大值,最大值为=3100(元),
故答案为:3100元.
18.
【分析】先把点坐标代入中求出得到反比例函数解析式,再利用反比例函数解析式确定点坐标,然后结合函数图像,写出反比例函数图像在一次函数图像下方所对应的自变量的范围即可.
【详解】解:∵,在反比例函数的图像上,
∴,
解得:,
∴反比例函数解析式为,
当时,,即,
∴,
∴当时,的取值范围是.
故答案为:.
三、解答题
19.(1)解:由题意得,
;
(2)解:当时,,
当时,,
,
在每一象限内,y随x的增大而减小,
当时,.
20.(1)解:设反比例函数式,
∵把代入反比例函数式,
∴,
∴.
故答案为:.
(2)解:当,,
故答案为:3A;
(3)解:当A时,则,
∴,
∴用电器的可变电阻至少是.
21.(1)1)把点(k,—1)代入,得,
∴.
(2)∵在这个函数图象所在的每个象限内,y的值随x的值增大而减小,
∴
解得:.
22.(1)把代入得:,
∴反比例函数的解析式为,
把代入得:,
∴的坐标为,
∴,解得,
∴一次函数的解析式为,
(2)把代入中,得,
∴点的坐标为
∵点的纵坐标等于6,
∴,
∴,
∴点的坐标为或.
23.解:(1)根据题意知:
(2)当时,
即商店要想每天获得利润21元,单价应定为每件元或元.
(3)∵
∴当时,y取得最大值,最大值为,
答:商店要想每天获得最大利润,单价应定为每件元,最大利润为元.
24.(1)解:∵点在反比例函数的图象上,
,即,
∴反比例函数解析式为:,
∵点在反比例函数的图象上,
,
∴点A的坐标为,
、在一次函数的图象上,可得:
,解得,
∴一次函数解析式为:.
(2)解:如图,一次函数的图象与x轴交于点,
,
.
(3)解:,
,
∴由图象可知,x的取值范围是:或.
一、单选题
1.下列哪个点在反比例函数的图像上?( )
A. B. C. D.
2.若函数为反比例函数,则m的值是( )
A.1 B.0 C. D.
3.点,,都在反比例函数的图象上,则,,大小关系是( )
A. B. C. D.
4.反比例函数(为常数)的图象位于第一、三象限,则的取值范围是( )
A. B. C. D.
5.若函数的图象在第一、三象限内,则的取值范围是( )
A. B. C. D.
6.已知点,在反比例函数的图象上,且,则下列结论一定正确的是( )
A. B. C. D.
7.如图,已知点A为反比例函数的图象上一点,过点A作轴,垂足为B,若的面积为1,则k的值为( )
A.1 B. C.2 D.
8.对于反比例函数,下列说法正确的是( )
A.图象经过点 B.图象位于第一、三象限
C.当时,y随x的增大而增大 D.当时,y随x的增大而增大
9.一次函数和反比例函数在同一直角坐标系中的图像可能是( )
A. B. C. D.
10.下面的三个问题中都有两个变量:
①正方形的周长y与边长x;
②一种容积为的圆柱形量筒,量筒的底面积与量筒的高
③小赵骑行到公司上班,他骑行的平均速度y与骑行时间x;
其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是( )
A.②③ B.①② C.①③ D.①②③
二、填空题
11.已知点P(1,)在反比例函数y=(k≠0)的图像上,则k的值是 .
12.反比例函数图像经过、,且,那么的取值范围是 .
13.已知直线与双曲线的一个交点的坐标为,则它们的另一个交点的坐标是 .
14.在平面直角坐标系中,反比例函数的图像过点和点,则的值为 .
15.如图,两个反比例函数和(其中)在第一象限内的图象依次是和,设点P在上,轴于点C,交于点A,轴于点D,交于点B,则四边形的面积为 .
16.如图,点A、B是反比例函数y=(x>0)图象上的两点,且A、B两点的纵坐标分别为2和1,C在x轴上,AC=BC,∠ACB=90°,则k= .
17.某商店经营皮鞋,已知所获利润y(单位:元)与销售单价x(单价:元)之间的函数关系式为y=-x2+24x+2956,则获利最多为 元.
18.如图,一次函数与反比例函数的图像交于,两点.当时,的取值范围是 .
三、解答题
19.已知x,y满足下表.
x … 1 4 …
y … 4 1 …
(1)求y关于x的函数表达式:
(2)当时,求y的取值范围.
20.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)这个反比例函数的解析式是 ().
(2)若使用时电阻,则电流I是
(3)如果以蓄电池为电源的用电器的电流不能超过10A,那么用电器的可变电阻至少是多少?
21.已知反比例函数
(1)如果这个函数的图象经过点,求k的值;
(2)如果在这个函数图象所在的每个象限内,y的值随x的值增大而减小,求k的取值范围.
22.如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且的面积为,求点的坐标.
23.某商店以每件5元的价格购进一种文具,由试销知,该文具每天的销售量m(件)与单价x(元)之间满足一次函数关系.
(1)写出商店每天销售这种文具的利润y(元) 与单价x(元) 之间的函数关系式?
(2)商店要想每天获得利润21元,单价应定为多少元?
(3) 商店要想每天获得最大利润,单价应定为多少元?最大利润为多少?
24.如图,已知,是反比例函数的图象和一次函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出不等式的解集.
答案
一、单选题
1.D
【分析】根据反比例函数的图像上的点的横纵坐标乘积为4进行判断即可.
【详解】解:A.∵,∴不在反比例函数的图像上,故选项不符合题意;
B.∵,∴不在反比例函数的图像上,故选项不符合题意;
C.∵,∴不在反比例函数的图像上,故选项不符合题意;
D.∵,∴在反比例函数的图像上,故选项符合题意.
故选:D.
2.D
【分析】根据反比例函数的定义进行解答即可.
【详解】解:是反比例函数,
解得.
故选:D.
3.A
【分析】将点,,分别代入反比例函数,求得,,的值后,再来比较一下它们的大小.
【详解】解:∵点,,都在反比例函数的图象上,
∴,即,,即;,即,
∵,
∴;
故选:A.
4.B
【分析】根据反比例函数的性质可得m﹣2>0,进一步即可求出答案.
【详解】解:∵反比例函数(m为常数)的图象位于第一、三象限,
∴m﹣2>0,
解得:m>2.
故选:B.
5.A
【分析】根据反比例函数的性质得,然后解不等式即可.
【详解】解:根据题意得,
解得.
故选:A.
6.B
【分析】把点A和点B的坐标代入解析式,根据条件可判断出、的大小关系.
【详解】解:∵点,在反比例函数的图象上,
∴.
∵,
∴.
故选:B.
7.D
【分析】根据反比例函数的比例系数的几何意义可得,然后去绝对值即可得.
【详解】解:由反比例函数的图象可知,,
的面积为1,点为反比例函数的图象上一点,且轴,
,
解得或(舍去),
故选:D.
8.B
【分析】根据反比例函数的性质对各选项进行逐一分析即可.
【详解】解:,点不满足关系式,因此A选项不符合题意;
;
它的图象在第一、三象限,因此选项符合题意;
当时,它的图象在第三象限,随的增大而增小,因此C选项不符合题意;
当时,它的图象在第一象限,随的增大而增小,因此D选项不符合题意.
故选:B.
9.A
【分析】根据一次函数及反比例函数图像与性质逐项验证即可得到答案.
【详解】解:A、由一次函数图像可知,则,从而反比例函数图像在第一、三象限,该选项正确,符合题意;
B、由一次函数图像可知,则,从而反比例函数图像在第二、四象限,该选项错误,不符合题意;
C、由一次函数图像可知,则,从而反比例函数图像在第一、三象限,该选项错误,不符合题意;
D、由一次函数图像可知,则,从而反比例函数图像在第一、三象限,该选项错误,不符合题意;
故选:A.
10.A
【分析】分别求出三个问题中变量与变量之间的函数关系式即可得到答案.
【详解】解:①∵正方形的周长为,边长为,
∴,不符合题意;
②∵一种容积为的圆柱形量筒,量筒的底面积与量筒的高,
∴,即,符合题意;
③小赵骑行到公司上班,他骑行的平均速度为,骑行时间为,
∴,即,符合题意;
综上分析可知,变量y与变量x之间的函数关系可以用该图象表示的是②③,故B正确.
故选:B.
二、填空题
11..
【详解】试题分析:∵点P(1,)在反比例函数y=(k≠0)的图像上,
∴.
12.
【分析】直接利用反比例函数的增减性得出,进而求出答案.
【详解】解:∵反比例函数图像经过、,且,
∴每个象限内,随的增大而减小,
∴,
解得:,
∴的取值范围是.
故答案为:.
13.
【分析】根据反比例函数的图象是中心对称图形,则经过原点的直线的两个交点一定关于原点对称,即可求解.
【详解】解:∵直线与双曲线的一个交点的坐标为,且两图象的交点关于原点对称,
∴它们的另一个交点的坐标是.
故答案为:
14.
【分析】把点代入反比例函数解析式可求出反比例函数解析式,再把点代入计算即可.
【详解】解:∵反比例函数的图像过点,
∴,
∴反比例函数解析式为,
∵点在反比例函数,
∴,解得:,
故答案为:.
15.
【分析】根据反比例函数k值的意义,求出四边形的面积和,的面积即可得出答案.
【详解】解:∵,,
∴四边形的面积为:.
故答案为:.
16.6
【分析】过点A作AG⊥x轴于点G,过点B作BH⊥x轴于点H,易证△AGC≌CHB,根据全等三角形的性质,可得GC和CH的值,根据A、B的纵坐标,表示出横坐标,列方程求解即可.
【详解】过点A作AG⊥x轴于点G,过点B作BH⊥x轴于点H,如图所示,
则有∠AGC=∠CHB=90°,
∴∠GAC+∠GCA=90°,
∵∠ACB=90°,AC=BC,
∴∠ACG+∠HCB=90°,
∴∠GAC=∠HCB,
∴△AGC≌CHB(AAS),
∴AG=CH=2,GC=BH=1,∴GH=3
∵A、B在反比例函数的图象上,
∴,B(k,1),
∴,
∴k=6,
故答案为:6.
17.3100
【分析】根据抛物线的开口方向和顶点坐标的纵坐标公式即可求出结论.
【详解】解:∵a=-1,
∴y有最大值,最大值为=3100(元),
故答案为:3100元.
18.
【分析】先把点坐标代入中求出得到反比例函数解析式,再利用反比例函数解析式确定点坐标,然后结合函数图像,写出反比例函数图像在一次函数图像下方所对应的自变量的范围即可.
【详解】解:∵,在反比例函数的图像上,
∴,
解得:,
∴反比例函数解析式为,
当时,,即,
∴,
∴当时,的取值范围是.
故答案为:.
三、解答题
19.(1)解:由题意得,
;
(2)解:当时,,
当时,,
,
在每一象限内,y随x的增大而减小,
当时,.
20.(1)解:设反比例函数式,
∵把代入反比例函数式,
∴,
∴.
故答案为:.
(2)解:当,,
故答案为:3A;
(3)解:当A时,则,
∴,
∴用电器的可变电阻至少是.
21.(1)1)把点(k,—1)代入,得,
∴.
(2)∵在这个函数图象所在的每个象限内,y的值随x的值增大而减小,
∴
解得:.
22.(1)把代入得:,
∴反比例函数的解析式为,
把代入得:,
∴的坐标为,
∴,解得,
∴一次函数的解析式为,
(2)把代入中,得,
∴点的坐标为
∵点的纵坐标等于6,
∴,
∴,
∴点的坐标为或.
23.解:(1)根据题意知:
(2)当时,
即商店要想每天获得利润21元,单价应定为每件元或元.
(3)∵
∴当时,y取得最大值,最大值为,
答:商店要想每天获得最大利润,单价应定为每件元,最大利润为元.
24.(1)解:∵点在反比例函数的图象上,
,即,
∴反比例函数解析式为:,
∵点在反比例函数的图象上,
,
∴点A的坐标为,
、在一次函数的图象上,可得:
,解得,
∴一次函数解析式为:.
(2)解:如图,一次函数的图象与x轴交于点,
,
.
(3)解:,
,
∴由图象可知,x的取值范围是:或.
