沪科版九年级数学上册试题第二十二章 相似形 单元测试卷(含解析)
文档属性
| 名称 | 沪科版九年级数学上册试题第二十二章 相似形 单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 22:46:23 | ||
图片预览



文档简介
第二十二章《相似形》单元测试卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.如图,下列推理错误的是( )
A.∵直线// ∴ B.∵,∴直线//
C.∵,∴直线//// D.∵直线////,∴
2.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( )
A.(20﹣x)2=20x B.x2=20(20﹣x)
C.x(20﹣x)=202 D.以上都不对
3.如图,在平行四边形ABCD中,、分别是边上两个三等分点,、分别交、、于、、,则( )
A.3:2:1 B.5:3:2 C.6:5:4 D.5:4:3
4.如图1是古希腊时期的巴台农神庙(Parthenom Temple),把图1中用虚线表示的矩形画成图2矩形,当以矩形的宽为边作正方形时,惊奇地发现矩形与矩形相似,则等于( )
A. B. C. D.
5.如图,三角形OAB的顶点、、,C是OB边的中点,过点C作交x轴于点D,将沿x轴向右平移,当点C的对应点恰好落在AB边上时,此时点D对应点的坐标为( )
A. B. C. D.
6.已知:中,为边中点,过点的直线交延长线于,交于,记,,则( )
A.2 B. C. D.1
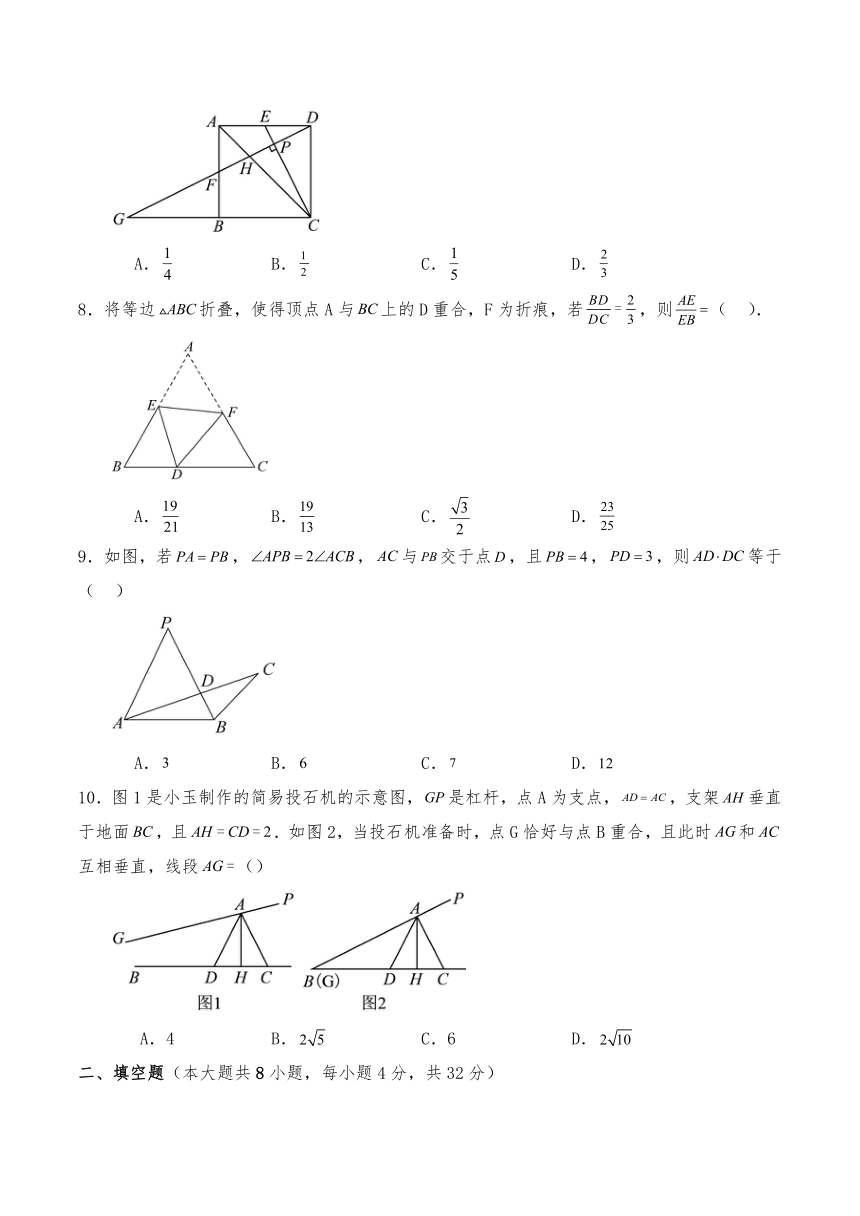
7.如图,正方形中,是中点,连接,,作交于,交于,交于,延长交延长线于,则的值为( )
A. B. C. D.
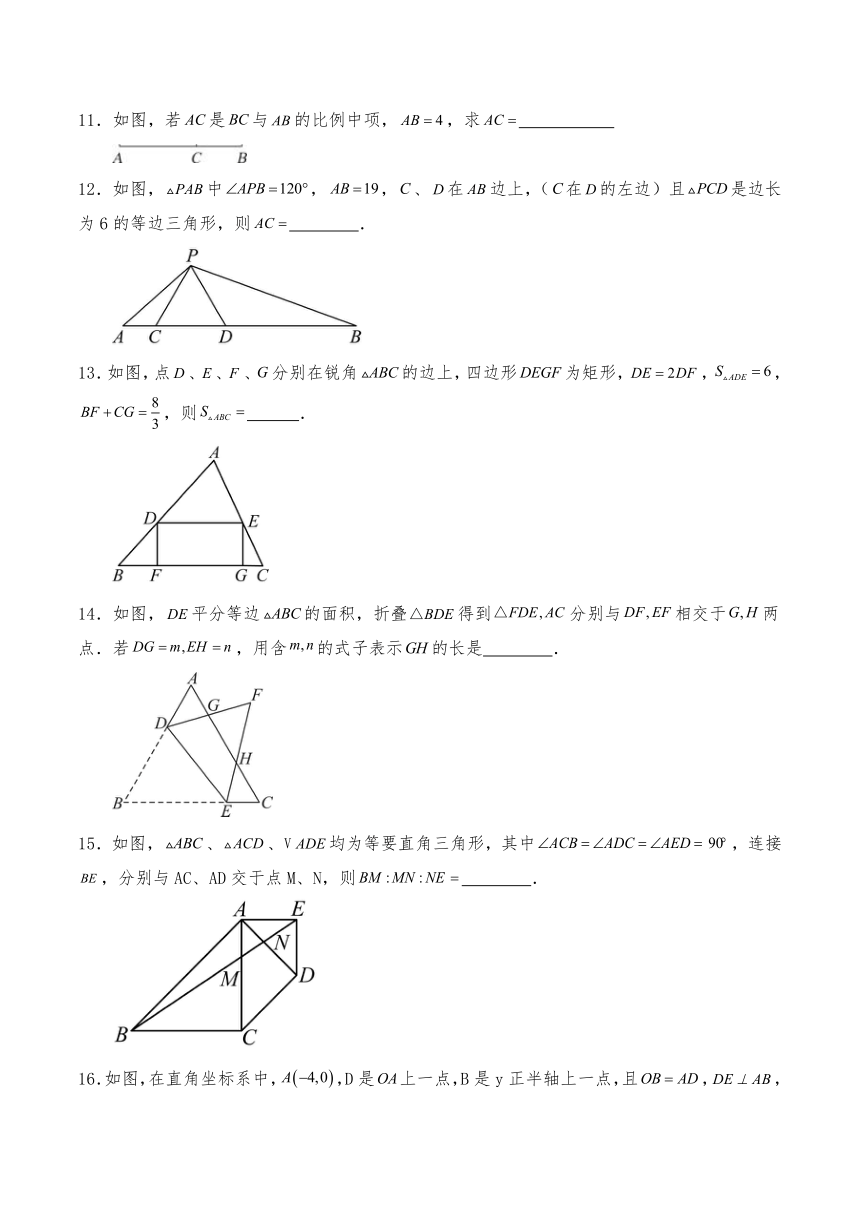
8.将等边折叠,使得顶点A与上的D重合,F为折痕,若,则( ).
A. B. C. D.
9.如图,若,,与交于点,且,,则等于( )
A. B. C. D.
10.图1是小玉制作的简易投石机的示意图,是杠杆,点A为支点,,支架垂直于地面,且.如图2,当投石机准备时,点G恰好与点B重合,且此时和互相垂直,线段()
A.4 B. C.6 D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.如图,若是与的比例中项,,求
12.如图,中,,、在边上,(在的左边)且是边长为6的等边三角形,则 .
13.如图,点、、、分别在锐角的边上,四边形为矩形,,,,则 .
14.如图,平分等边的面积,折叠得到分别与相交于两点.若,用含的式子表示的长是 .
15.如图,、、均为等要直角三角形,其中,连接,分别与AC、AD交于点M、N,则 .
16.如图,在直角坐标系中,,D是上一点,B是y正半轴上一点,且,,垂足为E,
(1)当D是的中点时, ;
(2)求的最小值 ;
17.如图,在中,,从左到右依次摆放三个正方形:,,,已知顶点,,在边上,顶点,,在边上,,,则的长为 .
18.如图,矩形中,,,点在的延长线上,,连接交于点,点在边上,,连接,点为中点,连接交于点,下列结论:①;②;③;④四边形的面积为,其中所有正确结论的序号为 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,已知点,分别在边,上,,交于点,,,,,.
(1)求的长; (2)若的面积为70,求的面积.
20.(8分)在梯形中,,,E为边上的任意一点,,且交于点F.
(1)当时, ______.(用含的代数式表示)
(2)当时,求的长.(用含和k的代数式表示)
21.(10分)如图,在边长为4的正方形中,点E在边上,且,连接,点F、G分别在、上.
(1)给定三个关系:①是的角平分线,②,③,从中选择两个作为条件,一个作为结论构成一个真命题,并说明理由;
(2)在(1)的条件下,求线段的长度.
22.(10分)已知不等臂跷跷板AB长为3米,当AB的一端点A碰到地面时,(如图1)点B离地高1.5米;当AB的另一端点B碰到地面时,(如图2)点A离地高1米,求跷跷板AB的支撑点O到地面的距离为多少米?
23.(10分)如图,在中,于点D,于点E,与相交于点F,
(1)求证:.
(2)连接,小明进行了深入探究,他发现,得到老师和同学们的认同,他利用(1)中的结论,具体推理过程如下:
∵
∴
∴
又∵
∴
请你仿照小明的方法证明.
24.(12分)如图,中,,,D为的中点,E为线段上一点,将绕点D逆时针旋转得到线段,连接,连接.
(1)如图1,当,位于线段同侧时,______;
(2)如图2,当,位于线段的异侧时,求的度数;
(3)在(2)的条件下,若与的交点为点G,若G为的三等分点,,请直接写出的长.
答案
一、单选题
1.C
【分析】根据平行线分线段成比例和相似三角形的判定与性质逐项分析即可得出答案.
解:A.∵直线// ∴,推理正确,故选项不符合题意;
B.∵,∴直线//,推理正确,故选项不符合题意;
C.∵,不能得出直线////,推理错误,故选项符合题意;
D.∵直线////,∴,推理正确,故选项不符合题意;
故选:C.
2.A
【分析】点P是AB的黄金分割点,且PB<PA,PB=x,则PA=20 x,则,即可求解.
解:由题意知,点P是AB的黄金分割点,
且PB<PA,PB=x,则PA=20 x,
∴,
∴(20 x)2=20x,
故选:A.
3.B
【分析】过作,交于,于,根据三角形中位线定理得到,得到,,得到、与的关系,求比即可.
解:过作,交于,于,
为中点,
是的中位线,
,,
,
,
,
,
,
是的中位线,
,
,
,
,,
,
故选:B.
4.D
【分析】根据相似图形的性质,列出比例式,进行求解即可.
解:∵矩形与矩形相似,
∴,
∵四边形为正方形,
∴,
∵,
∴,
∴,
∴,即:,
设,
则:,
解得:(负值已舍去);
∴;
故选D.
5.A
【分析】根据勾股定理可得,,由是的中点可得,,由题意可得:,可得,即可求得,即可求解.
解:∵、、
∴,,
∴
∵是的中点
∴,
∵,
∴
又∵
∴,
∴,即
解得
∵,,
将沿x轴向右平移,当点C的对应点恰好落在AB边上时,可知是将沿x轴向右平移了个单位长度
此时点对应的坐标为,即
故选:A
6.A
【分析】作交于,设,则,,先证,推出,再根据,得出,根据相似三角形对应边成比例可得,进而可得.
解:如图,作交于,
设,则,,
∵,
∴,,
又∵D为BC中点,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
∴.
故选A.
7.C
【分析】根据正方形的性质可证得,推出,证明,得出,证明,得出,设,则,求出,进而可得答案.
解:∵四边形是正方形,
∴,
∵,
∴,
∴,
∴,
∵是中点,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
设,
则,
∴,
∴;
故选:C.
8.A
【分析】设,然后利用相似三角形的性质:相似三角形的周长比等于相似比,即可求出,然后用k表示即可得到结果.
解:∵,
∴设,
∴,
∵为等边三角形,
∴,
∴,
∴,
∵,
∴,
故选:A
9.C
【分析】如图(见分析)所示,延长到,使,连结,则,根据等腰三角形的性质和三角形外角性质,可得,由于,则,于是可证明,然后利用相似三角形的相似比即可算出的值.
解:如图所示,延长到,使,连结
又∵,
∴
∴
∵,
∴
又∵,
∴
∴
即
故选C.
10.B
【分析】先求出及的长,再证明,再根据相似三角形的性质列比例式求解即可.
解:
,
,
,
,
又
∴=
∵=,
,
,
,
,
故选:B.
二、填空题
11.
【分析】由,求得,是与的比例中项,解一元二次方程即可求得,
解:∵,
∴,
∵是与的比例中项,
∴,即,
解得:,
∴
故答案为:
12.9或4
【分析】先根据等边三角形的性质及三角形的内角和定理得出,即可证明 PDB: ACP,再根据相似三角形的性质得出,求解即可.
解:∵是边长为6的等边三角形,
∴,,
∴,
∵,
∴,
∵,
∴,
∴ PDB: ACP,
∴,
∵,
∴,
∴,
解得或4,
故答案为:9或4.
13.
【分析】过点作于点,交于点,证明,根据相似三角形的性质得出,设,则,根据,得出,则,代入比例式进行计算,进而根据三角形的面积公式即可求解.
解:如图所示,过点作于点,交于点,
∵四边形为矩形,
∴,
∴,
∴,
∵,
设,则,
∵,
∴,
∴,
又∵,
∴,
整理得,
解得:,
∴,
故答案为:.
14.
【分析】先根据折叠的性质可得,,从而可得,再根据相似三角形的判定可证,根据相似三角形的性质可得,,然后将两个等式相加即可得.
解:是等边三角形,
,
∵折叠得到,
,
,,
平分等边的面积,
,
,
又,
,
,,
,
,
解得或(不符合题意,舍去),
故答案为:.
15.
【分析】如图所示,延长交于F,由等腰直角三角形的性质得到,,证明四边形是矩形,得到,,,,证明得到,则;进一步证明是等腰直角三角形,得到,证明,推出,设,则,,即可得到.
解:如图所示,延长交于F,
∵、、均为等要直角三角形,
∴,,
∴,
∴四边形是矩形,
∴,,,,
∴,
∴,
∴,
∵,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∴,
设,则,
∴,
∴,
故答案为:.
16.
【分析】(1)先求出,,在利用得出即可求出答案;
(2)当时,的值最小,此时点与点重合,根据直角三角形斜边上的中线等于斜边的一半即可求出的最小值.
解:(1)∵,
∴.
∵D是的中点,
∴.
∴.
∵,
∴.
又∵,
∴.
∴,即.
∴.
故答案是;
(2)∵点E在上,
∴当时,的值最小.
此时,点与点重合,如图
∵,,
∴.
∵,
∴是边上的中线.
∴.
故答案是.
17.6
【分析】根据正方形的性质及相似三角形的判定和性质得出,设正方形的边长为x,则,代入求解即可.
解:∵四边形,,为正方形,,,
∴,,
∴,
∴,
设正方形的边长为x,则,
∴,
解得:(负值舍去),
∴的长为6,
故答案为:6.
18.①②④
【分析】通过证明∽,可得,可证,故正确;由勾股定理可求,由等腰三角形的性质可求,故正确;求出时是等边三角形,可判断③错误;分别求出,,,的长,即可求四边形的面积为,故正确,即可求解.
解:,,,,
,,
,,
∽,
,
,故正确;
连接,
,
,
点是的中点,
,,,故正确;
∵,
,
若,则,
,
,
,
是等边三角形,
,与题意不符合,故错误;
,,
,
,
,
,,
四边形是平行四边形,
,
,
,
∽.
,
,
,,
四边形的面积,故正确;
故答案为:.
三、解答题
19.
解:(1),,,,
,
,
;
,
,
,;
(2)设点到的距离为,点到的距离为,
,
,
,
,
的面积是28.
20.
(1)解:如图,过A作,与交于G,与交于H,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴同理可得:,
,
∴,
∵,
∴,则,
∴;
(2)过A作,与交于G,与交于H,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴同理可得:,
,
∴,
∵,
∴,则,
∴.
21.
(1)解:①是的角平分线,②为条件,③为结论,
证明:∵是的角平分线,
∴,
∵,
∴,
∴,
∴;
(2)解:∵四边形是正方形,且,∴,,
∴,
作于点H,连接,
∵是的角平分线,,
∴,
又∵,
∴,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∴.
22.
解:如图所示:过点B作BN⊥AH于点N,AM⊥BH于点M,
可得HO∥BN,
则△AOH∽△ABN,
故,
∵AB长为3米,BN长为1.5米,
∴,
∴
同理可得:△BOH∽△BAM,
则,
∵AB长为3米,AM长为1米,
∴,即
∴OH=0.6,
答:跷跷板AB的支撑点O到地面的距离为0.6米.
23.
解:(1)证明:∵,,
∴,
∴,,
∴,
∴;
(2)证明:连接,
∵∠BEF=∠CDF=900,,
∴,
∴= ,
∴,
又∵,
∴.
24.
(1)解:取中点,连接,如图1所示:
点是的中点,
,
为的中点,
,
将绕点D逆时针旋转得到线段,
;
(2)解:取中点,连接,如图2所示:
点是的中点,
,
为的中点,
,
,
将绕点D逆时针旋转得到线段,
,
,
,
;
(3)解:①若:
有(2)可知:,
,
,
,
,
,为AB的中点,点是的中点,
,
,
,
,
,
,
;
②若:
,
,
,
;
综上所述:或.
一、单选题(本大题共10小题,每小题3分,共30分)
1.如图,下列推理错误的是( )
A.∵直线// ∴ B.∵,∴直线//
C.∵,∴直线//// D.∵直线////,∴
2.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( )
A.(20﹣x)2=20x B.x2=20(20﹣x)
C.x(20﹣x)=202 D.以上都不对
3.如图,在平行四边形ABCD中,、分别是边上两个三等分点,、分别交、、于、、,则( )
A.3:2:1 B.5:3:2 C.6:5:4 D.5:4:3
4.如图1是古希腊时期的巴台农神庙(Parthenom Temple),把图1中用虚线表示的矩形画成图2矩形,当以矩形的宽为边作正方形时,惊奇地发现矩形与矩形相似,则等于( )
A. B. C. D.
5.如图,三角形OAB的顶点、、,C是OB边的中点,过点C作交x轴于点D,将沿x轴向右平移,当点C的对应点恰好落在AB边上时,此时点D对应点的坐标为( )
A. B. C. D.
6.已知:中,为边中点,过点的直线交延长线于,交于,记,,则( )
A.2 B. C. D.1
7.如图,正方形中,是中点,连接,,作交于,交于,交于,延长交延长线于,则的值为( )
A. B. C. D.
8.将等边折叠,使得顶点A与上的D重合,F为折痕,若,则( ).
A. B. C. D.
9.如图,若,,与交于点,且,,则等于( )
A. B. C. D.
10.图1是小玉制作的简易投石机的示意图,是杠杆,点A为支点,,支架垂直于地面,且.如图2,当投石机准备时,点G恰好与点B重合,且此时和互相垂直,线段()
A.4 B. C.6 D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.如图,若是与的比例中项,,求
12.如图,中,,、在边上,(在的左边)且是边长为6的等边三角形,则 .
13.如图,点、、、分别在锐角的边上,四边形为矩形,,,,则 .
14.如图,平分等边的面积,折叠得到分别与相交于两点.若,用含的式子表示的长是 .
15.如图,、、均为等要直角三角形,其中,连接,分别与AC、AD交于点M、N,则 .
16.如图,在直角坐标系中,,D是上一点,B是y正半轴上一点,且,,垂足为E,
(1)当D是的中点时, ;
(2)求的最小值 ;
17.如图,在中,,从左到右依次摆放三个正方形:,,,已知顶点,,在边上,顶点,,在边上,,,则的长为 .
18.如图,矩形中,,,点在的延长线上,,连接交于点,点在边上,,连接,点为中点,连接交于点,下列结论:①;②;③;④四边形的面积为,其中所有正确结论的序号为 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,已知点,分别在边,上,,交于点,,,,,.
(1)求的长; (2)若的面积为70,求的面积.
20.(8分)在梯形中,,,E为边上的任意一点,,且交于点F.
(1)当时, ______.(用含的代数式表示)
(2)当时,求的长.(用含和k的代数式表示)
21.(10分)如图,在边长为4的正方形中,点E在边上,且,连接,点F、G分别在、上.
(1)给定三个关系:①是的角平分线,②,③,从中选择两个作为条件,一个作为结论构成一个真命题,并说明理由;
(2)在(1)的条件下,求线段的长度.
22.(10分)已知不等臂跷跷板AB长为3米,当AB的一端点A碰到地面时,(如图1)点B离地高1.5米;当AB的另一端点B碰到地面时,(如图2)点A离地高1米,求跷跷板AB的支撑点O到地面的距离为多少米?
23.(10分)如图,在中,于点D,于点E,与相交于点F,
(1)求证:.
(2)连接,小明进行了深入探究,他发现,得到老师和同学们的认同,他利用(1)中的结论,具体推理过程如下:
∵
∴
∴
又∵
∴
请你仿照小明的方法证明.
24.(12分)如图,中,,,D为的中点,E为线段上一点,将绕点D逆时针旋转得到线段,连接,连接.
(1)如图1,当,位于线段同侧时,______;
(2)如图2,当,位于线段的异侧时,求的度数;
(3)在(2)的条件下,若与的交点为点G,若G为的三等分点,,请直接写出的长.
答案
一、单选题
1.C
【分析】根据平行线分线段成比例和相似三角形的判定与性质逐项分析即可得出答案.
解:A.∵直线// ∴,推理正确,故选项不符合题意;
B.∵,∴直线//,推理正确,故选项不符合题意;
C.∵,不能得出直线////,推理错误,故选项符合题意;
D.∵直线////,∴,推理正确,故选项不符合题意;
故选:C.
2.A
【分析】点P是AB的黄金分割点,且PB<PA,PB=x,则PA=20 x,则,即可求解.
解:由题意知,点P是AB的黄金分割点,
且PB<PA,PB=x,则PA=20 x,
∴,
∴(20 x)2=20x,
故选:A.
3.B
【分析】过作,交于,于,根据三角形中位线定理得到,得到,,得到、与的关系,求比即可.
解:过作,交于,于,
为中点,
是的中位线,
,,
,
,
,
,
,
是的中位线,
,
,
,
,,
,
故选:B.
4.D
【分析】根据相似图形的性质,列出比例式,进行求解即可.
解:∵矩形与矩形相似,
∴,
∵四边形为正方形,
∴,
∵,
∴,
∴,
∴,即:,
设,
则:,
解得:(负值已舍去);
∴;
故选D.
5.A
【分析】根据勾股定理可得,,由是的中点可得,,由题意可得:,可得,即可求得,即可求解.
解:∵、、
∴,,
∴
∵是的中点
∴,
∵,
∴
又∵
∴,
∴,即
解得
∵,,
将沿x轴向右平移,当点C的对应点恰好落在AB边上时,可知是将沿x轴向右平移了个单位长度
此时点对应的坐标为,即
故选:A
6.A
【分析】作交于,设,则,,先证,推出,再根据,得出,根据相似三角形对应边成比例可得,进而可得.
解:如图,作交于,
设,则,,
∵,
∴,,
又∵D为BC中点,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
∴.
故选A.
7.C
【分析】根据正方形的性质可证得,推出,证明,得出,证明,得出,设,则,求出,进而可得答案.
解:∵四边形是正方形,
∴,
∵,
∴,
∴,
∴,
∵是中点,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
设,
则,
∴,
∴;
故选:C.
8.A
【分析】设,然后利用相似三角形的性质:相似三角形的周长比等于相似比,即可求出,然后用k表示即可得到结果.
解:∵,
∴设,
∴,
∵为等边三角形,
∴,
∴,
∴,
∵,
∴,
故选:A
9.C
【分析】如图(见分析)所示,延长到,使,连结,则,根据等腰三角形的性质和三角形外角性质,可得,由于,则,于是可证明,然后利用相似三角形的相似比即可算出的值.
解:如图所示,延长到,使,连结
又∵,
∴
∴
∵,
∴
又∵,
∴
∴
即
故选C.
10.B
【分析】先求出及的长,再证明,再根据相似三角形的性质列比例式求解即可.
解:
,
,
,
,
又
∴=
∵=,
,
,
,
,
故选:B.
二、填空题
11.
【分析】由,求得,是与的比例中项,解一元二次方程即可求得,
解:∵,
∴,
∵是与的比例中项,
∴,即,
解得:,
∴
故答案为:
12.9或4
【分析】先根据等边三角形的性质及三角形的内角和定理得出,即可证明 PDB: ACP,再根据相似三角形的性质得出,求解即可.
解:∵是边长为6的等边三角形,
∴,,
∴,
∵,
∴,
∵,
∴,
∴ PDB: ACP,
∴,
∵,
∴,
∴,
解得或4,
故答案为:9或4.
13.
【分析】过点作于点,交于点,证明,根据相似三角形的性质得出,设,则,根据,得出,则,代入比例式进行计算,进而根据三角形的面积公式即可求解.
解:如图所示,过点作于点,交于点,
∵四边形为矩形,
∴,
∴,
∴,
∵,
设,则,
∵,
∴,
∴,
又∵,
∴,
整理得,
解得:,
∴,
故答案为:.
14.
【分析】先根据折叠的性质可得,,从而可得,再根据相似三角形的判定可证,根据相似三角形的性质可得,,然后将两个等式相加即可得.
解:是等边三角形,
,
∵折叠得到,
,
,,
平分等边的面积,
,
,
又,
,
,,
,
,
解得或(不符合题意,舍去),
故答案为:.
15.
【分析】如图所示,延长交于F,由等腰直角三角形的性质得到,,证明四边形是矩形,得到,,,,证明得到,则;进一步证明是等腰直角三角形,得到,证明,推出,设,则,,即可得到.
解:如图所示,延长交于F,
∵、、均为等要直角三角形,
∴,,
∴,
∴四边形是矩形,
∴,,,,
∴,
∴,
∴,
∵,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∴,
设,则,
∴,
∴,
故答案为:.
16.
【分析】(1)先求出,,在利用得出即可求出答案;
(2)当时,的值最小,此时点与点重合,根据直角三角形斜边上的中线等于斜边的一半即可求出的最小值.
解:(1)∵,
∴.
∵D是的中点,
∴.
∴.
∵,
∴.
又∵,
∴.
∴,即.
∴.
故答案是;
(2)∵点E在上,
∴当时,的值最小.
此时,点与点重合,如图
∵,,
∴.
∵,
∴是边上的中线.
∴.
故答案是.
17.6
【分析】根据正方形的性质及相似三角形的判定和性质得出,设正方形的边长为x,则,代入求解即可.
解:∵四边形,,为正方形,,,
∴,,
∴,
∴,
设正方形的边长为x,则,
∴,
解得:(负值舍去),
∴的长为6,
故答案为:6.
18.①②④
【分析】通过证明∽,可得,可证,故正确;由勾股定理可求,由等腰三角形的性质可求,故正确;求出时是等边三角形,可判断③错误;分别求出,,,的长,即可求四边形的面积为,故正确,即可求解.
解:,,,,
,,
,,
∽,
,
,故正确;
连接,
,
,
点是的中点,
,,,故正确;
∵,
,
若,则,
,
,
,
是等边三角形,
,与题意不符合,故错误;
,,
,
,
,
,,
四边形是平行四边形,
,
,
,
∽.
,
,
,,
四边形的面积,故正确;
故答案为:.
三、解答题
19.
解:(1),,,,
,
,
;
,
,
,;
(2)设点到的距离为,点到的距离为,
,
,
,
,
的面积是28.
20.
(1)解:如图,过A作,与交于G,与交于H,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴同理可得:,
,
∴,
∵,
∴,则,
∴;
(2)过A作,与交于G,与交于H,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴同理可得:,
,
∴,
∵,
∴,则,
∴.
21.
(1)解:①是的角平分线,②为条件,③为结论,
证明:∵是的角平分线,
∴,
∵,
∴,
∴,
∴;
(2)解:∵四边形是正方形,且,∴,,
∴,
作于点H,连接,
∵是的角平分线,,
∴,
又∵,
∴,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∴.
22.
解:如图所示:过点B作BN⊥AH于点N,AM⊥BH于点M,
可得HO∥BN,
则△AOH∽△ABN,
故,
∵AB长为3米,BN长为1.5米,
∴,
∴
同理可得:△BOH∽△BAM,
则,
∵AB长为3米,AM长为1米,
∴,即
∴OH=0.6,
答:跷跷板AB的支撑点O到地面的距离为0.6米.
23.
解:(1)证明:∵,,
∴,
∴,,
∴,
∴;
(2)证明:连接,
∵∠BEF=∠CDF=900,,
∴,
∴= ,
∴,
又∵,
∴.
24.
(1)解:取中点,连接,如图1所示:
点是的中点,
,
为的中点,
,
将绕点D逆时针旋转得到线段,
;
(2)解:取中点,连接,如图2所示:
点是的中点,
,
为的中点,
,
,
将绕点D逆时针旋转得到线段,
,
,
,
;
(3)解:①若:
有(2)可知:,
,
,
,
,
,为AB的中点,点是的中点,
,
,
,
,
,
,
;
②若:
,
,
,
;
综上所述:或.
