二十二章二次函数 单元测试题(无答案) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 二十二章二次函数 单元测试题(无答案) 2024-2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 332.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 14:39:26 | ||
图片预览


文档简介
二十二章二次函数 单元测试题 2024-2025学年人教版数学九年级上册
一、单选题
1.若二次函数的图象经过点,则a的值为( )
A.-2 B.2 C.-1 D.1
2.若A(-4, ),B(-1, ),C(2, )为二次函数y=- +4x+5图象上的三点,则 、 、 的大小关系是( )
A. < < B. < <
C. < < D. < <
3.二次函数 的图象大致是( )
A. B.
C. D.
4.已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1,y1)、Q(x2,y2)两点.若x1<m≤x2,则a的取值范围为( )
A.﹣4≤a<﹣ B.﹣4≤a≤﹣
C.﹣ ≤a<0 D.﹣ <a<0
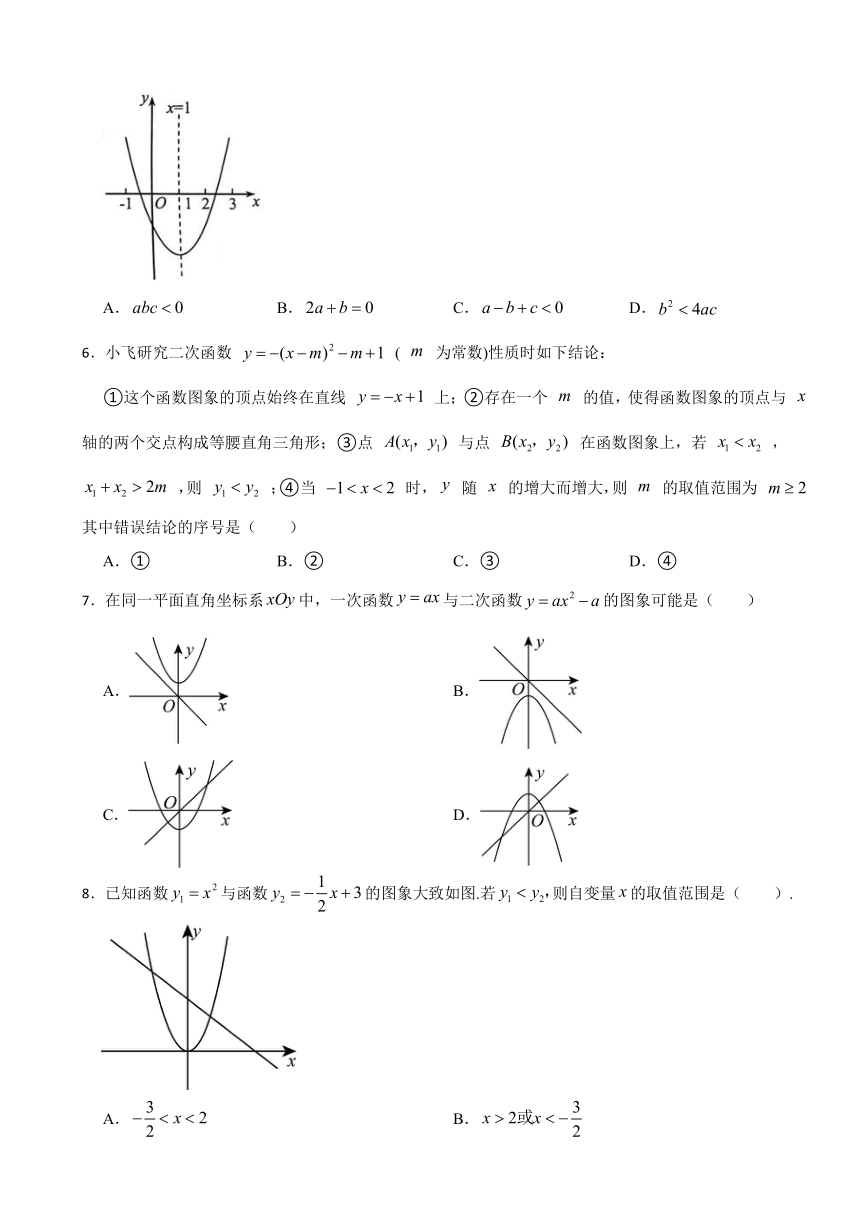
5.二次函数的图象如图所示,则下列结论正确的是( )
A. B. C. D.
6.小飞研究二次函数 ( 为常数)性质时如下结论:
①这个函数图象的顶点始终在直线 上;②存在一个 的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;③点 与点 在函数图象上,若 , ,则 ;④当 时, 随 的增大而增大,则 的取值范围为 其中错误结论的序号是( )
A.① B.② C.③ D.④
7.在同一平面直角坐标系中,一次函数与二次函数的图象可能是( )
A. B.
C. D.
8.已知函数与函数的图象大致如图.若则自变量的取值范围是( ).
A. B.
C. D.
9.在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )
A.(﹣2,3) B.(﹣1,4) C.(1,4) D.(4,3)
10.函数的自变量的取值范围为全体实数,其中部分的图象如图所示,对于此函数有下列结论:①函数图象关于轴对称;②函数既有最大值,也有最小值;③当时,随的增大而增大;④当时,关于的方程有4个实数根.其中正确的结论个数是( )
A.3 B.2 C.1 D.0
二、填空题
11.抛物线y=ax2经过点(2,﹣3),则a= .
12.如图,正方形OABC的边长为 ,OC与y轴的正半轴的夹角为15°,点B在抛物线y=ax2(a>0)的图象上,则a的值为 .
13.如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
14.二次函数的图像一部分如图所示,且顶点在第四象限,令,则S的取值范围是 .
15.关于 的方程 的解是 = , = ( 、 、 为常数, 0),则方程 的解是 .
三、解答题
16.已知抛物线经过点.
(1)求抛物线的表达式;
(2)判断点是否在抛物线上,请说明理由.
17.在平面直角坐标系中.二次函数图象的表达式为,其中.
(1)若此函数图象过点,求这个二次函数的表达式.
(2)若和为此二次函数图枲上两个不同点.当时,,求的值.
(3)已知,若点(1.)在此二次函数图象上,且当时随的增大而减小,求的范围.
18.平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,﹣);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(,0),且BC=5,AC=3(如图(1)).
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图(1)、图(2)中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
19.某商场将进价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至70元范围内,这种台灯的售价每上涨1元,其销售量就减少10个.为了实现每月获得最大的销售利润,这种台灯的售价应定为多少?最大利润为多少元?
20.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
21.请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
22.图1是一座拱桥,拱桥的拱形呈抛物线形状,在拱桥中,当水面宽度为米时,水面离桥洞最大距离为4米,如图2,以水平面为x轴,点O为原点建立平面直角坐标系.
(1)求该拱桥抛物线的解析式.
(2)当河水上涨,水面离桥洞的最大距离为1米时,求拱桥内水面的宽度.
23.如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,-3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
一、单选题
1.若二次函数的图象经过点,则a的值为( )
A.-2 B.2 C.-1 D.1
2.若A(-4, ),B(-1, ),C(2, )为二次函数y=- +4x+5图象上的三点,则 、 、 的大小关系是( )
A. < < B. < <
C. < < D. < <
3.二次函数 的图象大致是( )
A. B.
C. D.
4.已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1,y1)、Q(x2,y2)两点.若x1<m≤x2,则a的取值范围为( )
A.﹣4≤a<﹣ B.﹣4≤a≤﹣
C.﹣ ≤a<0 D.﹣ <a<0
5.二次函数的图象如图所示,则下列结论正确的是( )
A. B. C. D.
6.小飞研究二次函数 ( 为常数)性质时如下结论:
①这个函数图象的顶点始终在直线 上;②存在一个 的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;③点 与点 在函数图象上,若 , ,则 ;④当 时, 随 的增大而增大,则 的取值范围为 其中错误结论的序号是( )
A.① B.② C.③ D.④
7.在同一平面直角坐标系中,一次函数与二次函数的图象可能是( )
A. B.
C. D.
8.已知函数与函数的图象大致如图.若则自变量的取值范围是( ).
A. B.
C. D.
9.在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )
A.(﹣2,3) B.(﹣1,4) C.(1,4) D.(4,3)
10.函数的自变量的取值范围为全体实数,其中部分的图象如图所示,对于此函数有下列结论:①函数图象关于轴对称;②函数既有最大值,也有最小值;③当时,随的增大而增大;④当时,关于的方程有4个实数根.其中正确的结论个数是( )
A.3 B.2 C.1 D.0
二、填空题
11.抛物线y=ax2经过点(2,﹣3),则a= .
12.如图,正方形OABC的边长为 ,OC与y轴的正半轴的夹角为15°,点B在抛物线y=ax2(a>0)的图象上,则a的值为 .
13.如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
14.二次函数的图像一部分如图所示,且顶点在第四象限,令,则S的取值范围是 .
15.关于 的方程 的解是 = , = ( 、 、 为常数, 0),则方程 的解是 .
三、解答题
16.已知抛物线经过点.
(1)求抛物线的表达式;
(2)判断点是否在抛物线上,请说明理由.
17.在平面直角坐标系中.二次函数图象的表达式为,其中.
(1)若此函数图象过点,求这个二次函数的表达式.
(2)若和为此二次函数图枲上两个不同点.当时,,求的值.
(3)已知,若点(1.)在此二次函数图象上,且当时随的增大而减小,求的范围.
18.平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,﹣);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(,0),且BC=5,AC=3(如图(1)).
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图(1)、图(2)中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
19.某商场将进价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至70元范围内,这种台灯的售价每上涨1元,其销售量就减少10个.为了实现每月获得最大的销售利润,这种台灯的售价应定为多少?最大利润为多少元?
20.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
21.请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
22.图1是一座拱桥,拱桥的拱形呈抛物线形状,在拱桥中,当水面宽度为米时,水面离桥洞最大距离为4米,如图2,以水平面为x轴,点O为原点建立平面直角坐标系.
(1)求该拱桥抛物线的解析式.
(2)当河水上涨,水面离桥洞的最大距离为1米时,求拱桥内水面的宽度.
23.如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,-3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
