2024-2025学年浙江省杭州十四中高二(上)限时训练数学试卷(一)(含答案)
文档属性
| 名称 | 2024-2025学年浙江省杭州十四中高二(上)限时训练数学试卷(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 84.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 00:00:00 | ||
图片预览


文档简介
2024-2025学年浙江省杭州十四中高二(上)限时训练数学试卷(一)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数满足,则复数的虚部为( )
A. B. C. D.
2.已知为空间的一组基底,则下列向量也能作为空间的一组基底的是( )
A. ,, B. ,,
C. ,, D. ,,
3.某产品售后服务中心选取了个工作日,分别记录了每个工作日接到的客户服务电话的数量单位:次:,则这组数据的( )
A. 众数是 B. 分位数是
C. 极差是 D. 中位数是
4.已知直线:,:,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.已知,,,,则点到平面的距离为( )
A. B. C. D.
6.著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休”事实上,有很多代数问题可以转化为几何问题加以解决,如:可以转化为平面上点与点的距离结合上述观点,可得的最小值为( )
A. B. C. D.
7.某校课外活动期间开展跳绳、踢毽子、韵律操三项活动,甲、乙两位同学各自任选其中一项参加,则他们选择同一项活动的概率是( )
A. B. C. D.
8.过定点的直线与过定点的直线交于点,则的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 直线的倾斜角的取值范围是
B. “”是“直线与直线互相垂直”的充要条件
C. 两个非零向量与任何一个向量都不能构成空间的一个基底,则这两个向量共线
D. 已知向量,,则在上的投影向量为
10.某社团开展“建党周年主题活动学党史知识竞赛”,甲、乙两人能得满分的概率分别为,,两人能否获得满分相互独立,则( )
A. 两人均获得满分的概率 B. 两人至少一人获得满分的概率
C. 两人恰好只有甲获得满分的概率 D. 两人至多一人获得满分的概率
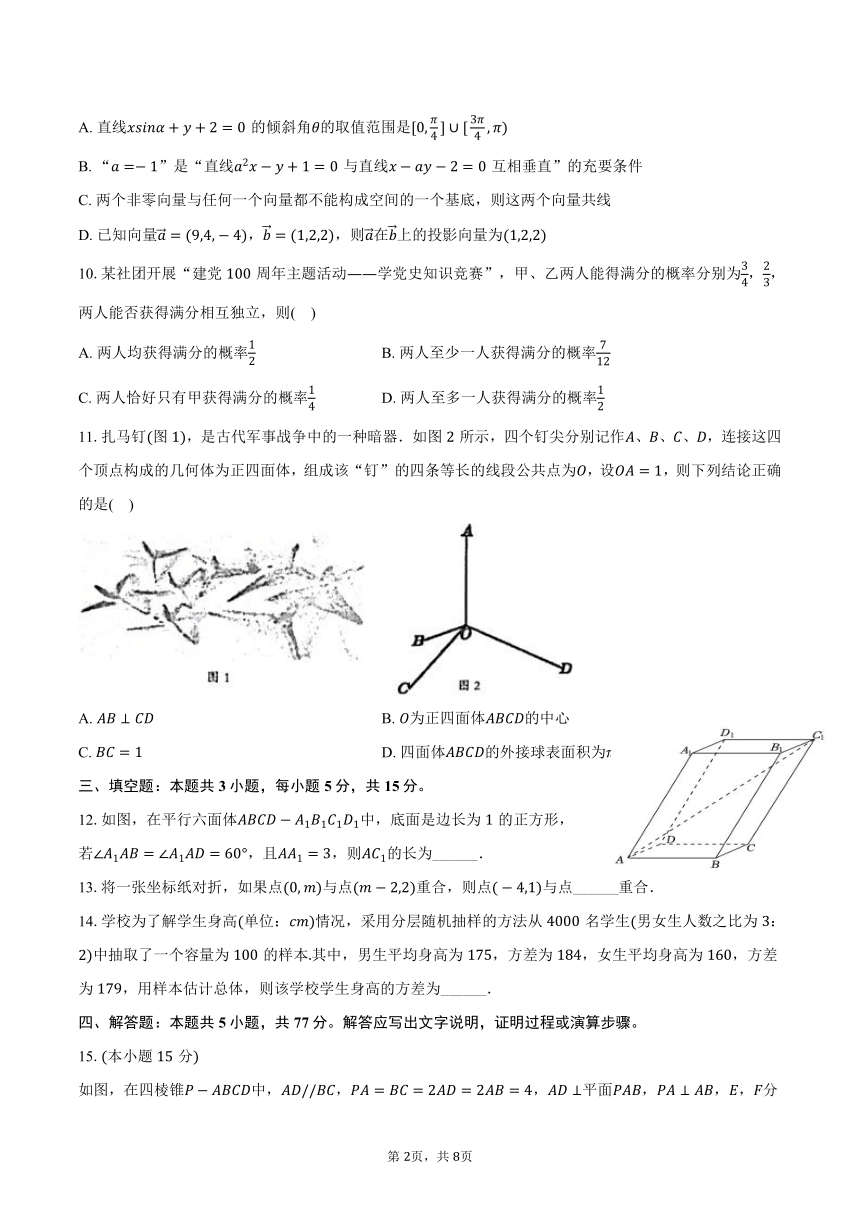
11.扎马钉图,是古代军事战争中的一种暗器.如图所示,四个钉尖分别记作、、、,连接这四个顶点构成的几何体为正四面体,组成该“钉”的四条等长的线段公共点为,设,则下列结论正确的是( )
A. B. 为正四面体的中心
C. D. 四面体的外接球表面积为
三、填空题:本题共3小题,每小题5分,共15分。
12.如图,在平行六面体中,底面是边长为的正方形,
若,且,则的长为______.
13.将一张坐标纸对折,如果点与点重合,则点与点______重合.
14.学校为了解学生身高单位:情况,采用分层随机抽样的方法从名学生男女生人数之比为:中抽取了一个容量为的样本其中,男生平均身高为,方差为,女生平均身高为,方差为,用样本估计总体,则该学校学生身高的方差为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在四棱锥中,,,平面,,,分别是棱,的中点.
证明:平面.
求平面与平面的夹角的正弦值.
16.本小题分
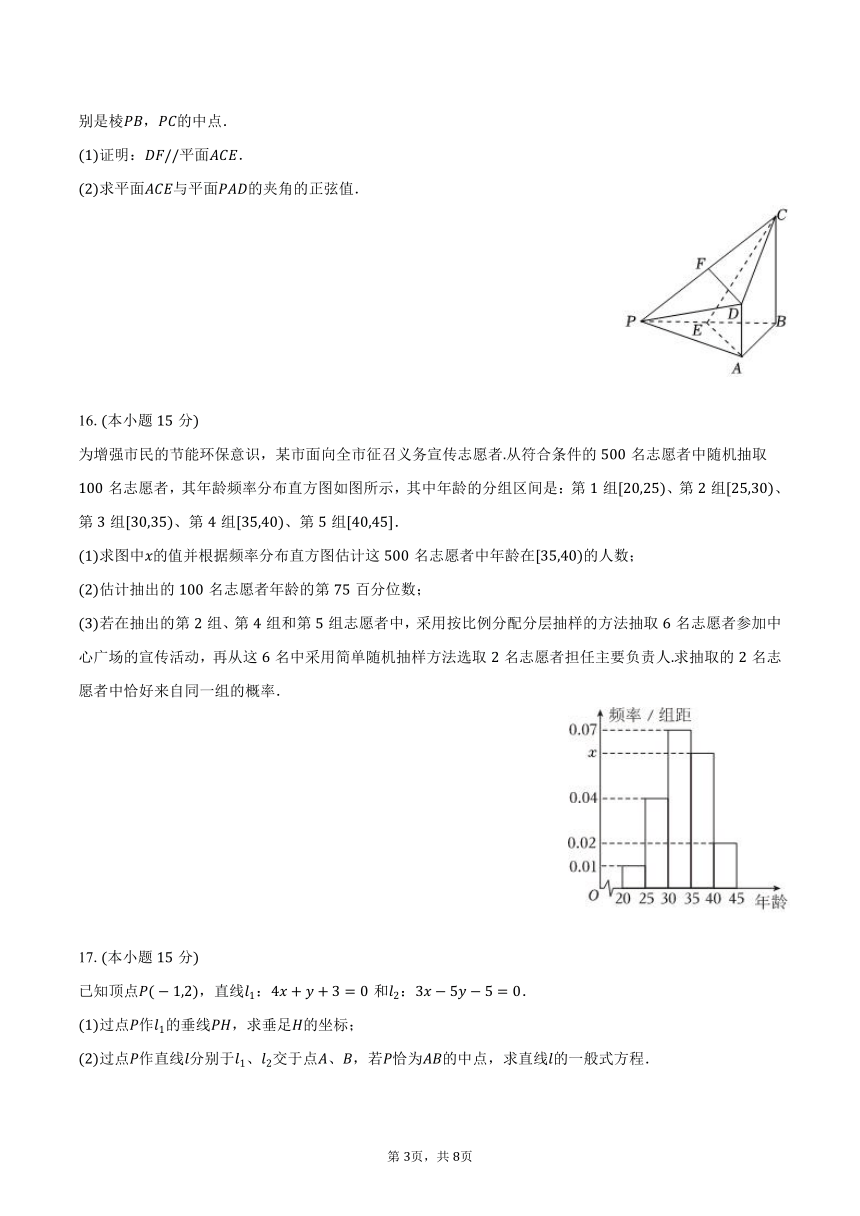
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者从符合条件的名志愿者中随机抽取名志愿者,其年龄频率分布直方图如图所示,其中年龄的分组区间是:第组、第组、第组、第组、第组.
求图中的值并根据频率分布直方图估计这名志愿者中年龄在的人数;
估计抽出的名志愿者年龄的第百分位数;
若在抽出的第组、第组和第组志愿者中,采用按比例分配分层抽样的方法抽取名志愿者参加中心广场的宣传活动,再从这名中采用简单随机抽样方法选取名志愿者担任主要负责人求抽取的名志愿者中恰好来自同一组的概率.
17.本小题分
已知顶点,直线:和:.
过点作的垂线,求垂足的坐标;
过点作直线分别于、交于点、,若恰为的中点,求直线的一般式方程.
18.本小题分
已知函数满足,且在上有最大值.
求,的值;
当时,不等式恒成立,求实数的取值范围.
19.本小题分
已知中,角,,的对边分别是,,,.
若,求的值;
若的平分线交于点,且,求周长的最小值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:证明:因为,分别为,的中点,
所以,,
又因为,
所以,
又,
所以,,
所以,
所以,
所以四边形为平行四边形,
所以,
又面,面,
所以面.
以为原点,,,所在直线分别为轴,轴,轴,建立空间直角坐标系:
则,,,,,,
平面的法向量为,
又,,
设面的法向量,
所以,
令,则,,
所以面的法向量,
设平面与平面的夹角为,
,,
所以,
所以平面与平面的夹角的正弦值为.
16.解:由直方图知:,可得,
所以名志愿者中年龄在的人数为人;
因为,,
所以第百分位数在区间内,若该数为,
所以,
解得;
由题设,第组、第组和第组的频率之比为::,知名志愿者有名来自,名来自,名来自,
不妨设第组、第组和第组抽取的志愿者为,,,,,,
则抽取两人的基本事件有,,,,,,,,,,,,,,,共个,
所以抽取的名志愿者中恰好来自同一组的概率.
17.解:由于过点作的垂线,所以直线的方程为,整理得;
所以,解得,即
直线与已知直线:和:分别交于和,
由于点在直线上,
故可设,由于点为和的中点,
所以;
由于点在直线上,故;
解得;
故A,.
由点和的坐标求出直线的方程为.
18.解:,满足:,
,即,
,
在上有最大值.
即 ,
由得,;
由得的解析式,
由题意得当,则只有当或时,才有意义,
当时,,等价为,
等价为的最大值,
即,得,舍去.
当时,由得,
即,
设,
当时,,得,
当时,,得舍,
综上,的取值范围为.
19.解:已知中,角,,的对边分别是,,,.
若,
所以,整理得:,
整理得:,
解得.
的平分线交于点,且,
利用三角形的面积:
所以,
整理得,
所以,
当且仅当时,等号成立.
所以,解得,
所以周长的最小值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数满足,则复数的虚部为( )
A. B. C. D.
2.已知为空间的一组基底,则下列向量也能作为空间的一组基底的是( )
A. ,, B. ,,
C. ,, D. ,,
3.某产品售后服务中心选取了个工作日,分别记录了每个工作日接到的客户服务电话的数量单位:次:,则这组数据的( )
A. 众数是 B. 分位数是
C. 极差是 D. 中位数是
4.已知直线:,:,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.已知,,,,则点到平面的距离为( )
A. B. C. D.
6.著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休”事实上,有很多代数问题可以转化为几何问题加以解决,如:可以转化为平面上点与点的距离结合上述观点,可得的最小值为( )
A. B. C. D.
7.某校课外活动期间开展跳绳、踢毽子、韵律操三项活动,甲、乙两位同学各自任选其中一项参加,则他们选择同一项活动的概率是( )
A. B. C. D.
8.过定点的直线与过定点的直线交于点,则的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 直线的倾斜角的取值范围是
B. “”是“直线与直线互相垂直”的充要条件
C. 两个非零向量与任何一个向量都不能构成空间的一个基底,则这两个向量共线
D. 已知向量,,则在上的投影向量为
10.某社团开展“建党周年主题活动学党史知识竞赛”,甲、乙两人能得满分的概率分别为,,两人能否获得满分相互独立,则( )
A. 两人均获得满分的概率 B. 两人至少一人获得满分的概率
C. 两人恰好只有甲获得满分的概率 D. 两人至多一人获得满分的概率
11.扎马钉图,是古代军事战争中的一种暗器.如图所示,四个钉尖分别记作、、、,连接这四个顶点构成的几何体为正四面体,组成该“钉”的四条等长的线段公共点为,设,则下列结论正确的是( )
A. B. 为正四面体的中心
C. D. 四面体的外接球表面积为
三、填空题:本题共3小题,每小题5分,共15分。
12.如图,在平行六面体中,底面是边长为的正方形,
若,且,则的长为______.
13.将一张坐标纸对折,如果点与点重合,则点与点______重合.
14.学校为了解学生身高单位:情况,采用分层随机抽样的方法从名学生男女生人数之比为:中抽取了一个容量为的样本其中,男生平均身高为,方差为,女生平均身高为,方差为,用样本估计总体,则该学校学生身高的方差为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在四棱锥中,,,平面,,,分别是棱,的中点.
证明:平面.
求平面与平面的夹角的正弦值.
16.本小题分
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者从符合条件的名志愿者中随机抽取名志愿者,其年龄频率分布直方图如图所示,其中年龄的分组区间是:第组、第组、第组、第组、第组.
求图中的值并根据频率分布直方图估计这名志愿者中年龄在的人数;
估计抽出的名志愿者年龄的第百分位数;
若在抽出的第组、第组和第组志愿者中,采用按比例分配分层抽样的方法抽取名志愿者参加中心广场的宣传活动,再从这名中采用简单随机抽样方法选取名志愿者担任主要负责人求抽取的名志愿者中恰好来自同一组的概率.
17.本小题分
已知顶点,直线:和:.
过点作的垂线,求垂足的坐标;
过点作直线分别于、交于点、,若恰为的中点,求直线的一般式方程.
18.本小题分
已知函数满足,且在上有最大值.
求,的值;
当时,不等式恒成立,求实数的取值范围.
19.本小题分
已知中,角,,的对边分别是,,,.
若,求的值;
若的平分线交于点,且,求周长的最小值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:证明:因为,分别为,的中点,
所以,,
又因为,
所以,
又,
所以,,
所以,
所以,
所以四边形为平行四边形,
所以,
又面,面,
所以面.
以为原点,,,所在直线分别为轴,轴,轴,建立空间直角坐标系:
则,,,,,,
平面的法向量为,
又,,
设面的法向量,
所以,
令,则,,
所以面的法向量,
设平面与平面的夹角为,
,,
所以,
所以平面与平面的夹角的正弦值为.
16.解:由直方图知:,可得,
所以名志愿者中年龄在的人数为人;
因为,,
所以第百分位数在区间内,若该数为,
所以,
解得;
由题设,第组、第组和第组的频率之比为::,知名志愿者有名来自,名来自,名来自,
不妨设第组、第组和第组抽取的志愿者为,,,,,,
则抽取两人的基本事件有,,,,,,,,,,,,,,,共个,
所以抽取的名志愿者中恰好来自同一组的概率.
17.解:由于过点作的垂线,所以直线的方程为,整理得;
所以,解得,即
直线与已知直线:和:分别交于和,
由于点在直线上,
故可设,由于点为和的中点,
所以;
由于点在直线上,故;
解得;
故A,.
由点和的坐标求出直线的方程为.
18.解:,满足:,
,即,
,
在上有最大值.
即 ,
由得,;
由得的解析式,
由题意得当,则只有当或时,才有意义,
当时,,等价为,
等价为的最大值,
即,得,舍去.
当时,由得,
即,
设,
当时,,得,
当时,,得舍,
综上,的取值范围为.
19.解:已知中,角,,的对边分别是,,,.
若,
所以,整理得:,
整理得:,
解得.
的平分线交于点,且,
利用三角形的面积:
所以,
整理得,
所以,
当且仅当时,等号成立.
所以,解得,
所以周长的最小值为.
第1页,共1页
同课章节目录
