人教版六年级数学上册分数乘法运算课件(共28张PPT)
文档属性
| 名称 | 人教版六年级数学上册分数乘法运算课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 08:01:33 | ||
图片预览





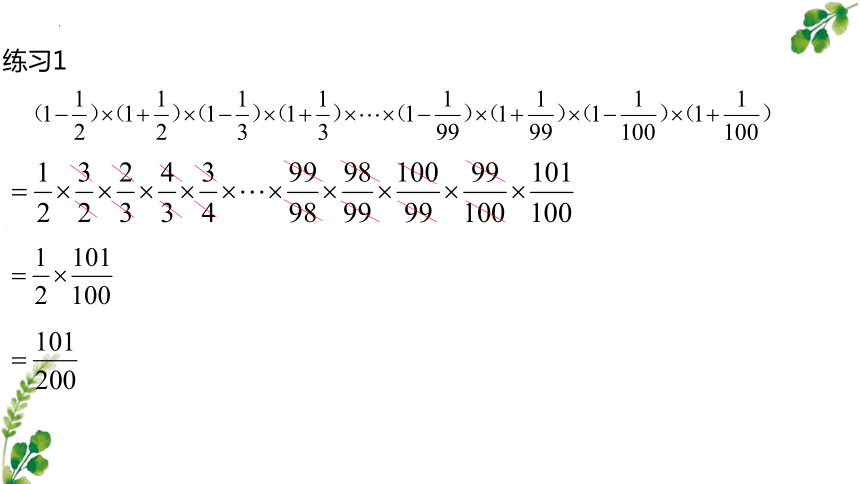


文档简介
(共28张PPT)
分数乘法运算(2)
连锁约分
分数裂差
本讲聚焦
导入
PART.01
连锁约分
1、算式中有多个因式相乘
2、将各个因式分别化成分子、分母相乘的形式
3、交叉约分(分子与分母约)
【连锁约分】
例题1
1、算式中有多个因式相乘
2、将各个因式分别化成分子、分母相乘的形式
3、交叉约分(分子与分母约)
练习1
找规律
2=1×2
6=2×3
12=3×4
20=4×5
30=5×6
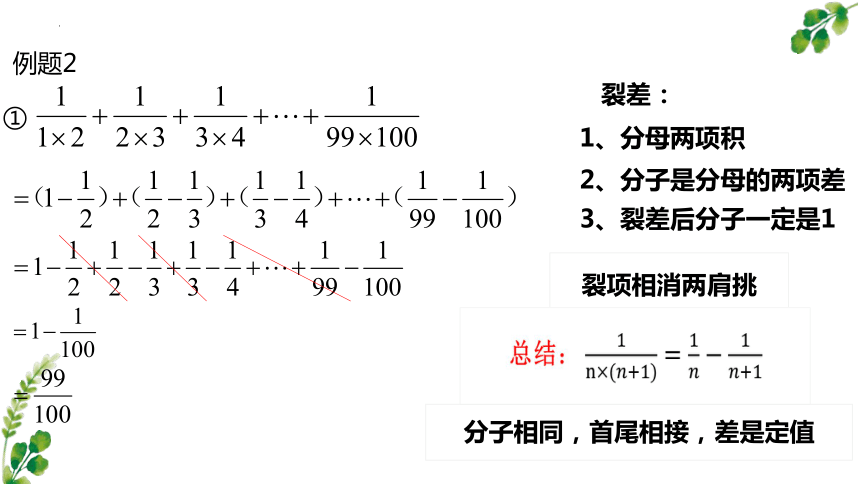
裂差:
1、分母两项积
2、分子是分母的两项差
3、裂差后分子一定是1
例题2
裂差:
1、分母两项积
2、分子是分母的两项差
3、裂差后分子一定是1
裂项相消两肩挑
分子相同,首尾相接,差是定值
①
②
裂项相消两肩挑
练习2
①
②
例题3
①
规律①:间接裂差第一种情况,分子为1.
分子不等于分母两数之间的差时,
差是几就提出一个几分之几到括号外面去,然后再裂差。
②
规律②:间接裂差第二种情况,分子不为1.
将分子提取到括号外面,然后按照规律①的步骤操作
练习3
①
②
例题4
①
总结:有时候分母并没有写成两数相乘,我们要学会将它拆成两个自然数相乘,注意保持首尾相接,差为定值。
练习4
①
②
例题5
①
8个1
总结:观察每个分数与谁接近,我们就用接近的那个数去表示,通常与1接近。
j即:1+分数单位 或 1-分数单位
练习5
①
8个1
综合巩固
THANKS
分数乘法运算(2)
连锁约分
分数裂差
本讲聚焦
导入
PART.01
连锁约分
1、算式中有多个因式相乘
2、将各个因式分别化成分子、分母相乘的形式
3、交叉约分(分子与分母约)
【连锁约分】
例题1
1、算式中有多个因式相乘
2、将各个因式分别化成分子、分母相乘的形式
3、交叉约分(分子与分母约)
练习1
找规律
2=1×2
6=2×3
12=3×4
20=4×5
30=5×6
裂差:
1、分母两项积
2、分子是分母的两项差
3、裂差后分子一定是1
例题2
裂差:
1、分母两项积
2、分子是分母的两项差
3、裂差后分子一定是1
裂项相消两肩挑
分子相同,首尾相接,差是定值
①
②
裂项相消两肩挑
练习2
①
②
例题3
①
规律①:间接裂差第一种情况,分子为1.
分子不等于分母两数之间的差时,
差是几就提出一个几分之几到括号外面去,然后再裂差。
②
规律②:间接裂差第二种情况,分子不为1.
将分子提取到括号外面,然后按照规律①的步骤操作
练习3
①
②
例题4
①
总结:有时候分母并没有写成两数相乘,我们要学会将它拆成两个自然数相乘,注意保持首尾相接,差为定值。
练习4
①
②
例题5
①
8个1
总结:观察每个分数与谁接近,我们就用接近的那个数去表示,通常与1接近。
j即:1+分数单位 或 1-分数单位
练习5
①
8个1
综合巩固
THANKS
