第二十一章 一元二次方程 单元 检测试题(含答案) 2024--2025学年人教版九年级数学上册
文档属性
| 名称 | 第二十一章 一元二次方程 单元 检测试题(含答案) 2024--2025学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 325.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 07:20:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十一章《一元二次方程》单元检测题
一.选择题(共10小题,每题3分,共30分)
1.若关于x的方程x2﹣m=0有实数根,则m的取值范围是( )
A.m<0 B.m≤0 C.m>0 D.m≥0
3.将一元二次方程﹣3x2﹣2=﹣4x化成一般形式ax2+bx+c=0(a>0)后,一次项和常数项分别是( )
A.﹣4,2 B.4x,﹣2 C.﹣4x,2 D.3x2,2
4.关于x的方程(m﹣3)x2﹣4x﹣2=0有两个不相等的实数根,则实数m的取值范围是( )
A.m≥1 B.m>1 C.m≥1且m≠3 D.m>1且m≠3
6.一元二次方程3x2﹣8x﹣a=0有一个根是x=3,则a的值及方程的另一个根是( )
A.a=3,x=1 B.a=3,x=﹣ C.a=﹣3,x=﹣ D.a=﹣1,x=﹣3
5.若方程x2﹣5x﹣1=0的两根为x1、x2,则+的值为( )
A.5 B. C.﹣5 D.
6. 已知(m2+n2)(m2+n2+2)-8=0,则m2+n2的值为( )
A. -4或2 B .-2或4 C. 4 D. 2
7.已知三角形的两边长为4和5,第三边的长是方程x2﹣5x+6=0的一个根,则这个三角形的周长是( )
A.11 B.12 C.11或12 D.15
8.已知a+,则的值为( )
A.﹣1 B.1 C.2 D.不能确定
9.如图,在△ABC中,∠B=90°,AB=4 cm,BC=3 cm,动点P,Q分别从点A,B同时开始移动(移动方式如图所示),点P的速度为 cm/s,点Q的速度为1 cm/s,点Q移动到点C后停止,点P也随之停止运动,若使△PBQ的面积为 cm2,则点P运动的时间是 ( )
A.2 s B.3 s C.4 s D.5 s
10.电影《流浪地球2》以提出计划将建造1万座行星发动机的时代为故事背景,讲述了“太阳危机”即将来袭,世界陷入一片恐慌之中,万座行星发动机正在建造中,人类将面临末日灾难与生命存续的双重挑战故事.一经上映就获得好评,第一天票房收入约5亿元,第三天票房收入达到了11.25亿元,设第一天到第三天票房收入平均每天增长的百分率为x,则可列方程 ( )
A.5(1+x)=11.25 B.5(1+2x)=11.25
C.5(1+x)2=11.25 D.5(1-x)2=11.25
二、填空题(每题3分,共24分)
11.一元二次方程x2-3x-10=0的一次项系数为 .
12.已知方程(m+1)x|m|+1=0是关于x的一元二次方程,则m的值是 .
13.已知m是方程x2-2x-7=0的一个根,则2m2-4m+1= .
14.已知一元二次方程x2+x﹣2021=0两根分别为m,n,则+值为 .
15.已知关于的一元二次方程有两个不相等的实数根,则实数的最大整数值为 .
16.设是方程的两实数根,则 .
17.关于x的方程有两个不相等的实数根,则a的取值范围是 .
18. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2,则修建的路宽应为 米.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解方程:
(1);
(2);
(3).
19.已知:关于x的一元二次方程.若此方程有两个实数根、,且,求k的值.
20.若关于的一元二次方程有一个根为,且,求的值.
22.已知等腰三角形的三边长分别为a,b,4,且a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,求m的值.
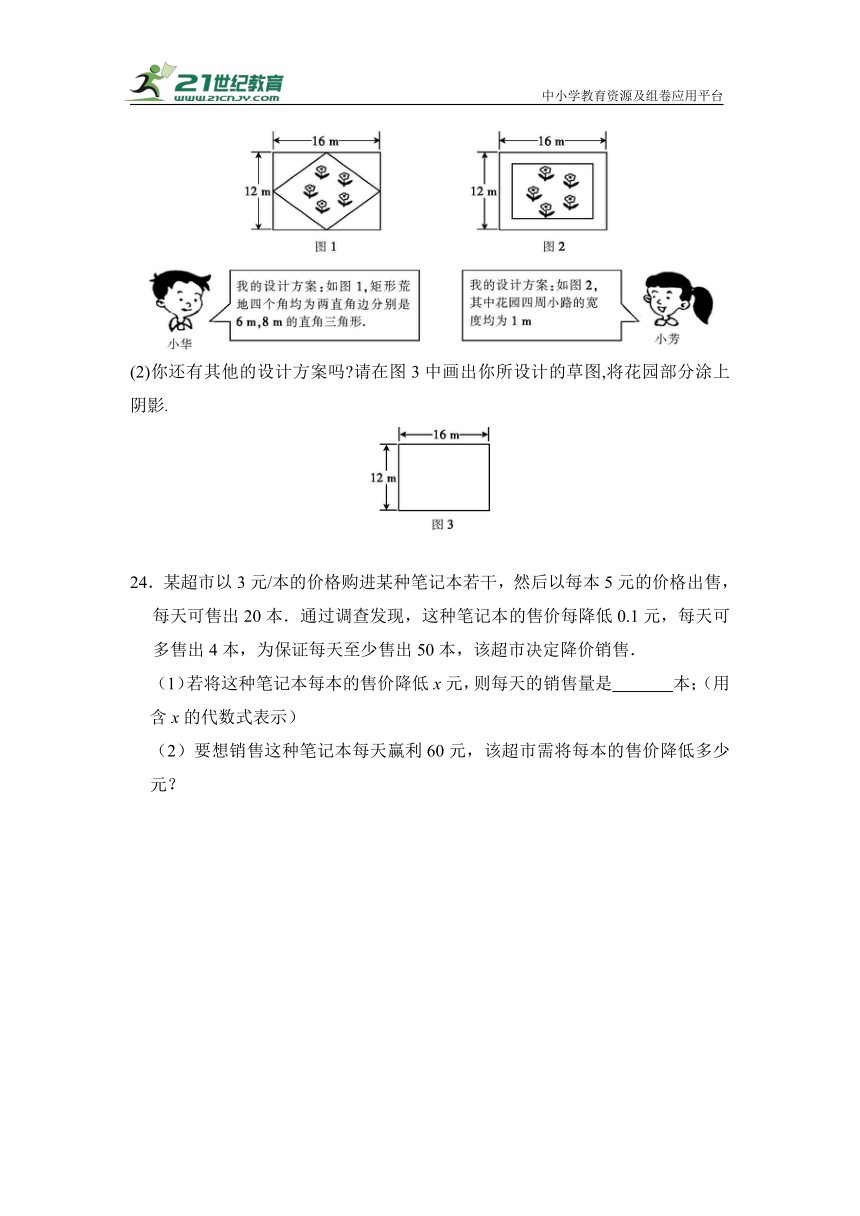
23.在一块长为16 m,宽为12 m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗 若不符合,请用列方程的方法说明理由.
(2)你还有其他的设计方案吗 请在图3中画出你所设计的草图,将花园部分涂上阴影.
24.某超市以3元/本的价格购进某种笔记本若干,然后以每本5元的价格出售,每天可售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若将这种笔记本每本的售价降低x元,则每天的销售量是 本;(用含x的代数式表示)
(2)要想销售这种笔记本每天赢利60元,该超市需将每本的售价降低多少元?
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B C B B C A D
二.填空题(共8小题)
11.-312.1 13.15
14.解:∵一元二次方程x2+x﹣2021=0的两根分别为m,n,
∴m+n=﹣1,mn=﹣2021,
∴+===,
故答案为:.
15.2
【分析】本题考查了一元二次方程的根的判别式与根的关系,熟练掌握根的判别式与根的关系式解答本题的关键.
令根的判别式大于0列不等式求解即可.
【详解】解:
由题意得,
解得,
∴实数m的最大整数值为2.
故答案为:2.
16.7
【分析】本题主要考查了一元二次方程的解,根与系数的关系,熟知一元二次方程的相关知识是解题的关键.
根据一元二次方程的解可得,根据根与系数的关系可得,再将化简即可求解.
【详解】解:∵是方程的两实数根,
∴,,即,
∴
,
故答案为:7.
17.且
18.1
三.解答题(共7小题)
19.(1),
(2),
(3),
20.0
【详解】试题分析:根据二次根式有意义的条件,可求出 的值,进而求出 的值,再将 与 的值代入一元二次方程,可求出 的值,最后将 的值代入代数式即可.
试题解析:根据二次根式有意义的条件,可得 ,解得 ,那么 .将代入方程可得 ,所以 ,则将 的值代入可得.
故本题的正确答案为0.
21.解:(1)∵方程有两个实数根x1,x2,
∴△=(2k﹣2)2﹣4k2≥0,
解得k≤;
(2)由根与系数关系知:x1+x2=2k﹣2,x1x2=k2,
∵k≤,
∴2k﹣2<0,
又|x1+x2|=x1x2﹣1,代入得,|2k﹣2|=k2﹣22,可化简为:k2+2k﹣24=0.
解得k=4(不合题意,舍去)或k=﹣6,
∴k=﹣6.
22.解:当a=4时,
∵a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+b=12,
∴b=8,
而4+4≠0,不符合题意;
当b=4时,
∵a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+a=12,
而4+4=8,不符合题意;
当a=b时,
∵a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴12=a+b,解得a=b=6,
∴m+2=36,
∴m=34.
23.解:(1)不符合. 1分
设小路的宽度均为x m.
根据题意得(16-2x)(12-2x)=×16×12,
解这个方程得x1=2,x2=12. 3分
但x2=12不符合题意,应舍去,∴x=2,
∴小芳的方案不符合条件,小路的宽度应均为2 m. 5分
(2)答案不唯一.
例如:如图所示.
24.解:(1)将这种笔记本每本的售价降低x元,则每天的销售量是20+×4=20+40x(本);
故答案为:(20+40x);
(2)设这种笔记本每本降价x元,
根据题意得:(5﹣3﹣x)(20+40x)=60,
2x2﹣3x+1=0,
解得:x=0.5或x=1,
当x=0.5时,销售量是20+40×0.5=40<50;
当x=1时,销售量是20+40=60>50.
∵每天至少售出50本,
∴x=1.
答:超市应将每本的销售价降低1元.
第二十一章《一元二次方程》单元检测题
一.选择题(共10小题,每题3分,共30分)
1.若关于x的方程x2﹣m=0有实数根,则m的取值范围是( )
A.m<0 B.m≤0 C.m>0 D.m≥0
3.将一元二次方程﹣3x2﹣2=﹣4x化成一般形式ax2+bx+c=0(a>0)后,一次项和常数项分别是( )
A.﹣4,2 B.4x,﹣2 C.﹣4x,2 D.3x2,2
4.关于x的方程(m﹣3)x2﹣4x﹣2=0有两个不相等的实数根,则实数m的取值范围是( )
A.m≥1 B.m>1 C.m≥1且m≠3 D.m>1且m≠3
6.一元二次方程3x2﹣8x﹣a=0有一个根是x=3,则a的值及方程的另一个根是( )
A.a=3,x=1 B.a=3,x=﹣ C.a=﹣3,x=﹣ D.a=﹣1,x=﹣3
5.若方程x2﹣5x﹣1=0的两根为x1、x2,则+的值为( )
A.5 B. C.﹣5 D.
6. 已知(m2+n2)(m2+n2+2)-8=0,则m2+n2的值为( )
A. -4或2 B .-2或4 C. 4 D. 2
7.已知三角形的两边长为4和5,第三边的长是方程x2﹣5x+6=0的一个根,则这个三角形的周长是( )
A.11 B.12 C.11或12 D.15
8.已知a+,则的值为( )
A.﹣1 B.1 C.2 D.不能确定
9.如图,在△ABC中,∠B=90°,AB=4 cm,BC=3 cm,动点P,Q分别从点A,B同时开始移动(移动方式如图所示),点P的速度为 cm/s,点Q的速度为1 cm/s,点Q移动到点C后停止,点P也随之停止运动,若使△PBQ的面积为 cm2,则点P运动的时间是 ( )
A.2 s B.3 s C.4 s D.5 s
10.电影《流浪地球2》以提出计划将建造1万座行星发动机的时代为故事背景,讲述了“太阳危机”即将来袭,世界陷入一片恐慌之中,万座行星发动机正在建造中,人类将面临末日灾难与生命存续的双重挑战故事.一经上映就获得好评,第一天票房收入约5亿元,第三天票房收入达到了11.25亿元,设第一天到第三天票房收入平均每天增长的百分率为x,则可列方程 ( )
A.5(1+x)=11.25 B.5(1+2x)=11.25
C.5(1+x)2=11.25 D.5(1-x)2=11.25
二、填空题(每题3分,共24分)
11.一元二次方程x2-3x-10=0的一次项系数为 .
12.已知方程(m+1)x|m|+1=0是关于x的一元二次方程,则m的值是 .
13.已知m是方程x2-2x-7=0的一个根,则2m2-4m+1= .
14.已知一元二次方程x2+x﹣2021=0两根分别为m,n,则+值为 .
15.已知关于的一元二次方程有两个不相等的实数根,则实数的最大整数值为 .
16.设是方程的两实数根,则 .
17.关于x的方程有两个不相等的实数根,则a的取值范围是 .
18. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2,则修建的路宽应为 米.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解方程:
(1);
(2);
(3).
19.已知:关于x的一元二次方程.若此方程有两个实数根、,且,求k的值.
20.若关于的一元二次方程有一个根为,且,求的值.
22.已知等腰三角形的三边长分别为a,b,4,且a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,求m的值.
23.在一块长为16 m,宽为12 m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗 若不符合,请用列方程的方法说明理由.
(2)你还有其他的设计方案吗 请在图3中画出你所设计的草图,将花园部分涂上阴影.
24.某超市以3元/本的价格购进某种笔记本若干,然后以每本5元的价格出售,每天可售出20本.通过调查发现,这种笔记本的售价每降低0.1元,每天可多售出4本,为保证每天至少售出50本,该超市决定降价销售.
(1)若将这种笔记本每本的售价降低x元,则每天的销售量是 本;(用含x的代数式表示)
(2)要想销售这种笔记本每天赢利60元,该超市需将每本的售价降低多少元?
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B C B B C A D
二.填空题(共8小题)
11.-312.1 13.15
14.解:∵一元二次方程x2+x﹣2021=0的两根分别为m,n,
∴m+n=﹣1,mn=﹣2021,
∴+===,
故答案为:.
15.2
【分析】本题考查了一元二次方程的根的判别式与根的关系,熟练掌握根的判别式与根的关系式解答本题的关键.
令根的判别式大于0列不等式求解即可.
【详解】解:
由题意得,
解得,
∴实数m的最大整数值为2.
故答案为:2.
16.7
【分析】本题主要考查了一元二次方程的解,根与系数的关系,熟知一元二次方程的相关知识是解题的关键.
根据一元二次方程的解可得,根据根与系数的关系可得,再将化简即可求解.
【详解】解:∵是方程的两实数根,
∴,,即,
∴
,
故答案为:7.
17.且
18.1
三.解答题(共7小题)
19.(1),
(2),
(3),
20.0
【详解】试题分析:根据二次根式有意义的条件,可求出 的值,进而求出 的值,再将 与 的值代入一元二次方程,可求出 的值,最后将 的值代入代数式即可.
试题解析:根据二次根式有意义的条件,可得 ,解得 ,那么 .将代入方程可得 ,所以 ,则将 的值代入可得.
故本题的正确答案为0.
21.解:(1)∵方程有两个实数根x1,x2,
∴△=(2k﹣2)2﹣4k2≥0,
解得k≤;
(2)由根与系数关系知:x1+x2=2k﹣2,x1x2=k2,
∵k≤,
∴2k﹣2<0,
又|x1+x2|=x1x2﹣1,代入得,|2k﹣2|=k2﹣22,可化简为:k2+2k﹣24=0.
解得k=4(不合题意,舍去)或k=﹣6,
∴k=﹣6.
22.解:当a=4时,
∵a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+b=12,
∴b=8,
而4+4≠0,不符合题意;
当b=4时,
∵a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+a=12,
而4+4=8,不符合题意;
当a=b时,
∵a,b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴12=a+b,解得a=b=6,
∴m+2=36,
∴m=34.
23.解:(1)不符合. 1分
设小路的宽度均为x m.
根据题意得(16-2x)(12-2x)=×16×12,
解这个方程得x1=2,x2=12. 3分
但x2=12不符合题意,应舍去,∴x=2,
∴小芳的方案不符合条件,小路的宽度应均为2 m. 5分
(2)答案不唯一.
例如:如图所示.
24.解:(1)将这种笔记本每本的售价降低x元,则每天的销售量是20+×4=20+40x(本);
故答案为:(20+40x);
(2)设这种笔记本每本降价x元,
根据题意得:(5﹣3﹣x)(20+40x)=60,
2x2﹣3x+1=0,
解得:x=0.5或x=1,
当x=0.5时,销售量是20+40×0.5=40<50;
当x=1时,销售量是20+40=60>50.
∵每天至少售出50本,
∴x=1.
答:超市应将每本的销售价降低1元.
同课章节目录
