第11章 三角形 单元测试题(含解析)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第11章 三角形 单元测试题(含解析)2024—2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 765.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 11:25:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1.以下列各组线段为边,能组成三角形的是( )
A.2cm,3cm,5cm B.5cm,6cm,10cm
C.1cm,1cm,3cm D.3cm,4cm,9cm
2.等腰三角形的一边长等于4,一边长等于9,则它的周长是( )
A.17 B.22 C.17或22 D.13
3.已知等腰三角形的一个角为75°,则其顶角为( )
A.30° B.75° C.105° D.30°或75°
4.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,∠A=46°,∠1=52°,则∠2=( )
A. 92° B. 94° C. 96° D. 98°
5.长度分别为 2 , 7 , x 的三条线段能组成一个三角形,x 的值可以是( )
A. B. C. D.
6.用下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A.1,2,3 B.1,1,2 C.1,2,2 D.1,5,7
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.如图,三边的中线,,的公共点为G.若,则图中阴影部分的面积是( )
A.8 B.10 C.12 D.6
9.如图,为估计池塘岸边A、B间的距离,小方在池塘的一侧选取一点O,
米,米,A、B间的距离不可能是( )
A.20米 B.23米 C.17米 D.26米
10.如图,点D,E分别在线段BC,AC上,连接AD,BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
二、填空题(每题3分,共24分)
11.已知三角形的三边长为连续整数,且周长为18cm,则它的最短边的长为____cm.
12.如图,三角形的面积是120平方厘米,且 ,D 是的中点, 则阴影部分的面积是 平方厘米.
13.如图,是的中线,E是的中点,连接,若的面积为24,则的面积为
14.如图,已知是的中线,,,则和的周长的差是 .
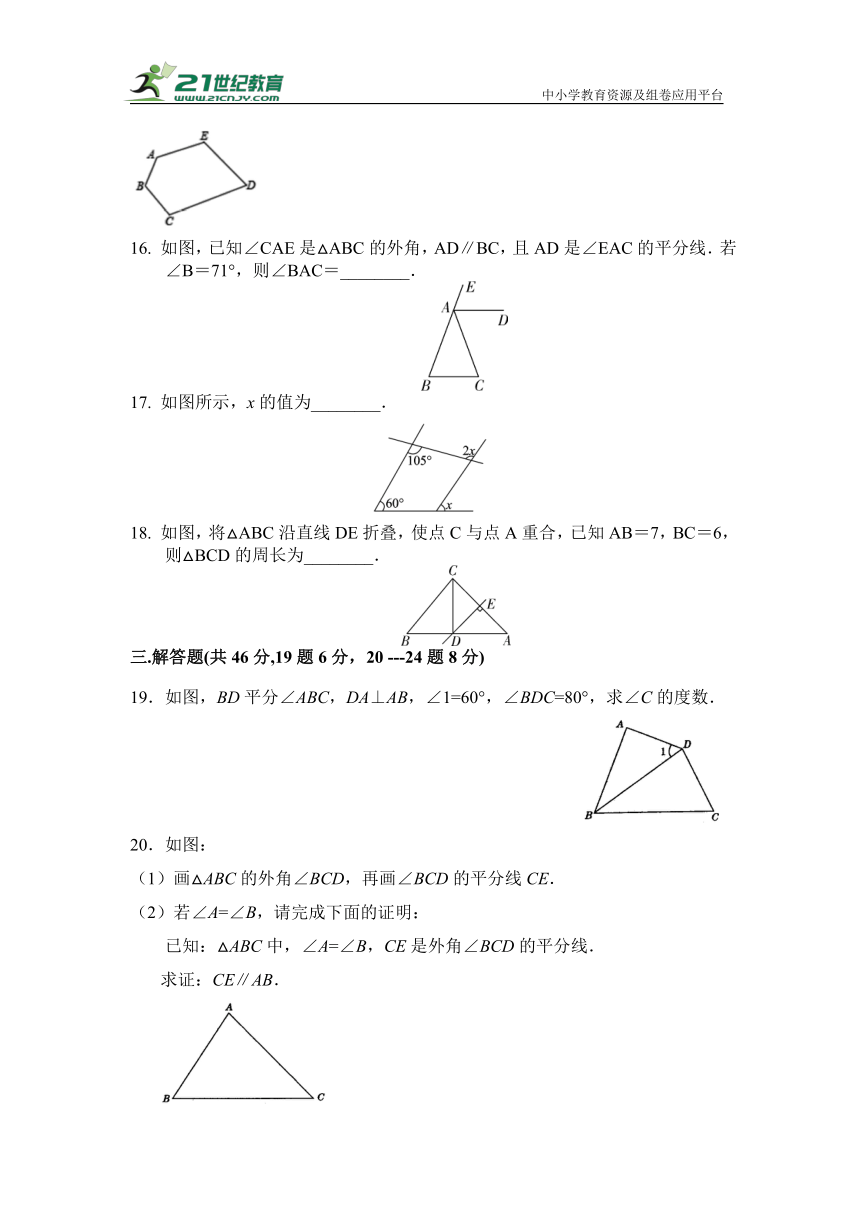
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16. 如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线.若∠B=71°,则∠BAC=________.
17. 如图所示,x的值为________.
18. 如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,BD平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C的度数.
20.如图:
(1)画△ABC的外角∠BCD,再画∠BCD的平分线CE.
(2)若∠A=∠B,请完成下面的证明:
已知:△ABC中,∠A=∠B,CE是外角∠BCD的平分线.
求证:CE∥AB.
21. 如图所示,求∠1的大小.
22. 如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?试说明你找出的规律的正确性.
23.如图,在中
(1)若平分,求证:
(2)若为边上的中线,且,求的取值范围.
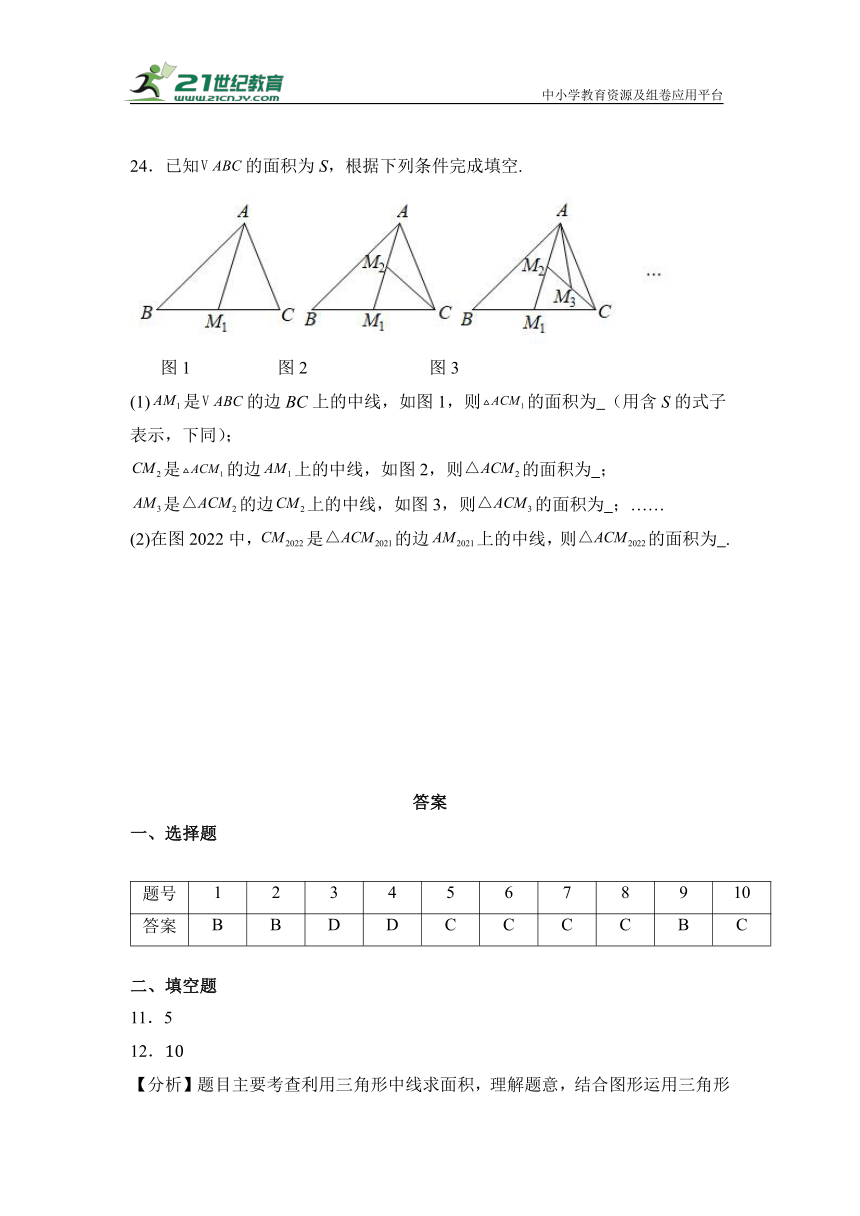
24.已知的面积为S,根据下列条件完成填空.
图1 图2 图3
(1)是的边BC上的中线,如图1,则的面积为 (用含S的式子表示,下同);
是的边上的中线,如图2,则的面积为 ;
是的边上的中线,如图3,则的面积为 ;……
(2)在图2022中,是的边上的中线,则的面积为 .
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D D C C C C B C
二、填空题
11.5
12.
【分析】题目主要考查利用三角形中线求面积,理解题意,结合图形运用三角形的高相等计算面积即可.
【详解】解:∵三角形的面积是平方厘米,D 是的中点,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
故答案为:.
13.6
【分析】本题主要考查了根据三角形的中线求三角形的面积,先根据三角形的中线求出,同理求出答案即可.
【详解】∵是的中线,,
∴.
∵E是的中点,
∴.
故答案为:6.
14.
【分析】根据三角形中线的定义可得,然后求出和的周长差,代入数据进行计算即可得解.
【详解】解:是的中线,
,
和的周长差
,,
和的周长差.
故答案为:.
【点睛】本题考查了三角形的中线的定义,熟记概念并求出和的周长差是解题的关键.
15.92°
16. 【答案】38° 【解析】∵AD∥BC,∠B=71°,∴∠EAD=∠B=71°.∵AD是∠EAC的平分线,∴∠EAC=2∠EAD=142°,∴∠BAC=180°-∠EAC=180°-142°=38°.
17. 【答案】55° [解析] 由多边形的外角和等于360°,得360°-105°-60°+x+2x=360°,解得x=55°.
18. 【答案】13 【解析】由折叠的性质可得:CD=AD,∴△BCD的周长=BC+CD+BD=BC+AD+BD=BC+BA=6+7=13.
三、解答题
19.解:在△ABD中,∵∠A=90°,∠1=60°,
∴∠ABD=90°-∠1=30°.
∵BD平分∠ABC,∴∠CBD=∠ABD=30°.
在△BDC中,∠C=180°-(∠BDC+∠CBD) =180°-(80°+30°)=70°.
20.(1)如答图
(2)证明:
∵∠A=∠B,∠BCD是△ABC的外角,
∴∠BCD=∠A+∠B=2∠B,
∵CE是外角∠BCD的平分线,
∴∠BCE=∠BCD=×2∠B=∠B,
∴CE∥AB(内错角相等,两直线平行)
点拨:如答图所示,要证明两直线平行,只需证内错角∠B=∠BCE即可.
21. 如图所示,求∠1的大小.
【考点】三角形的外角性质;对顶角、邻补角.
【分析】先根据邻补角的定义求得∠ACB,再根据三角形外角性质,求得∠1的度数即可.
【解答】解:如图所示,∵∠ACB=180°﹣140°=40°,且∠1是△ABC的外角,
∴∠1=∠A+∠ACB=80°+40°=120°.
【点评】本题主要考查了三角形的外角性质的运用,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.
22. 如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?试说明你找出的规律的正确性.
【考点】三角形内角和定理;翻折变换(折叠问题).
【分析】根据折叠得出∠ADE=∠A′DE,∠AED=∠A′ED,求出2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,推出∠ADE=90°﹣∠1,∠AED=90°﹣∠2,在△ADE中,∠A=180°﹣(∠AED+∠ADE),代入求出即可.
【解答】解:2∠A=∠1+∠2,
理由是:延长BD和CE交于A′,
∵把△ABC沿DE折叠,当点A落在四边形BCDE内部,
∴∠ADE=∠A′DE,∠AED=∠A′ED,
∴2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,
∴∠ADE=90°﹣∠1,∠AED=90°﹣∠2,
∵在△ADE中,∠A=180°﹣(∠AED+∠ADE),
∴∠A=∠1+∠2,
即2∠A=∠1+∠2.
【点评】本题考查了折叠的性质和三角形的内角和定理的应用,关键是得出等式∠ADE=90°﹣∠1,∠AED=90°﹣∠2,∠A=180°﹣(∠AED+∠ADE).
23.(1)见解析
(2)
【分析】本题考查角平分线的定义,三角形全等的判定与性质,三角形三边关系,正确作出辅助线构造三角形全等是解题的关键.
(1)在上取点E,使得,证明得到,由得到,根据三角形三边关系得到,即可证明结论;
(2)延长到点F,使得,连接,证明,得到,在中,利用三角形三边关系即可求解.
【详解】(1)证明:如图,在上取点E,使得,在与中,
平分,
,
,
,
,
,
,
,
;
(2)解:延长到点F,使得,连接,
,
,
为边上的中线,
,
,
,
,
,
在中,,
.
24.(1),,
(2)
【分析】(1)利用三角形的一条中线把三角形的面积分成相等的两部分求解即可;
(2)根据(1)中的求解可得规律,利用规律即可求解.
【详解】(1)解:∵是的边BC上的中线,的面积为S,如图1,
∴;
又∵是的边上的中线,如图2,
∴;
∵是的边上的中线,如图3,
∴,
故答案为:,,
(2)解:∵,
,
,
,
以此类推,
可得,
∴当时,,
故答案为:
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1.以下列各组线段为边,能组成三角形的是( )
A.2cm,3cm,5cm B.5cm,6cm,10cm
C.1cm,1cm,3cm D.3cm,4cm,9cm
2.等腰三角形的一边长等于4,一边长等于9,则它的周长是( )
A.17 B.22 C.17或22 D.13
3.已知等腰三角形的一个角为75°,则其顶角为( )
A.30° B.75° C.105° D.30°或75°
4.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,∠A=46°,∠1=52°,则∠2=( )
A. 92° B. 94° C. 96° D. 98°
5.长度分别为 2 , 7 , x 的三条线段能组成一个三角形,x 的值可以是( )
A. B. C. D.
6.用下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A.1,2,3 B.1,1,2 C.1,2,2 D.1,5,7
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.如图,三边的中线,,的公共点为G.若,则图中阴影部分的面积是( )
A.8 B.10 C.12 D.6
9.如图,为估计池塘岸边A、B间的距离,小方在池塘的一侧选取一点O,
米,米,A、B间的距离不可能是( )
A.20米 B.23米 C.17米 D.26米
10.如图,点D,E分别在线段BC,AC上,连接AD,BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
二、填空题(每题3分,共24分)
11.已知三角形的三边长为连续整数,且周长为18cm,则它的最短边的长为____cm.
12.如图,三角形的面积是120平方厘米,且 ,D 是的中点, 则阴影部分的面积是 平方厘米.
13.如图,是的中线,E是的中点,连接,若的面积为24,则的面积为
14.如图,已知是的中线,,,则和的周长的差是 .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16. 如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线.若∠B=71°,则∠BAC=________.
17. 如图所示,x的值为________.
18. 如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,BD平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C的度数.
20.如图:
(1)画△ABC的外角∠BCD,再画∠BCD的平分线CE.
(2)若∠A=∠B,请完成下面的证明:
已知:△ABC中,∠A=∠B,CE是外角∠BCD的平分线.
求证:CE∥AB.
21. 如图所示,求∠1的大小.
22. 如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?试说明你找出的规律的正确性.
23.如图,在中
(1)若平分,求证:
(2)若为边上的中线,且,求的取值范围.
24.已知的面积为S,根据下列条件完成填空.
图1 图2 图3
(1)是的边BC上的中线,如图1,则的面积为 (用含S的式子表示,下同);
是的边上的中线,如图2,则的面积为 ;
是的边上的中线,如图3,则的面积为 ;……
(2)在图2022中,是的边上的中线,则的面积为 .
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D D C C C C B C
二、填空题
11.5
12.
【分析】题目主要考查利用三角形中线求面积,理解题意,结合图形运用三角形的高相等计算面积即可.
【详解】解:∵三角形的面积是平方厘米,D 是的中点,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
故答案为:.
13.6
【分析】本题主要考查了根据三角形的中线求三角形的面积,先根据三角形的中线求出,同理求出答案即可.
【详解】∵是的中线,,
∴.
∵E是的中点,
∴.
故答案为:6.
14.
【分析】根据三角形中线的定义可得,然后求出和的周长差,代入数据进行计算即可得解.
【详解】解:是的中线,
,
和的周长差
,,
和的周长差.
故答案为:.
【点睛】本题考查了三角形的中线的定义,熟记概念并求出和的周长差是解题的关键.
15.92°
16. 【答案】38° 【解析】∵AD∥BC,∠B=71°,∴∠EAD=∠B=71°.∵AD是∠EAC的平分线,∴∠EAC=2∠EAD=142°,∴∠BAC=180°-∠EAC=180°-142°=38°.
17. 【答案】55° [解析] 由多边形的外角和等于360°,得360°-105°-60°+x+2x=360°,解得x=55°.
18. 【答案】13 【解析】由折叠的性质可得:CD=AD,∴△BCD的周长=BC+CD+BD=BC+AD+BD=BC+BA=6+7=13.
三、解答题
19.解:在△ABD中,∵∠A=90°,∠1=60°,
∴∠ABD=90°-∠1=30°.
∵BD平分∠ABC,∴∠CBD=∠ABD=30°.
在△BDC中,∠C=180°-(∠BDC+∠CBD) =180°-(80°+30°)=70°.
20.(1)如答图
(2)证明:
∵∠A=∠B,∠BCD是△ABC的外角,
∴∠BCD=∠A+∠B=2∠B,
∵CE是外角∠BCD的平分线,
∴∠BCE=∠BCD=×2∠B=∠B,
∴CE∥AB(内错角相等,两直线平行)
点拨:如答图所示,要证明两直线平行,只需证内错角∠B=∠BCE即可.
21. 如图所示,求∠1的大小.
【考点】三角形的外角性质;对顶角、邻补角.
【分析】先根据邻补角的定义求得∠ACB,再根据三角形外角性质,求得∠1的度数即可.
【解答】解:如图所示,∵∠ACB=180°﹣140°=40°,且∠1是△ABC的外角,
∴∠1=∠A+∠ACB=80°+40°=120°.
【点评】本题主要考查了三角形的外角性质的运用,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.
22. 如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?试说明你找出的规律的正确性.
【考点】三角形内角和定理;翻折变换(折叠问题).
【分析】根据折叠得出∠ADE=∠A′DE,∠AED=∠A′ED,求出2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,推出∠ADE=90°﹣∠1,∠AED=90°﹣∠2,在△ADE中,∠A=180°﹣(∠AED+∠ADE),代入求出即可.
【解答】解:2∠A=∠1+∠2,
理由是:延长BD和CE交于A′,
∵把△ABC沿DE折叠,当点A落在四边形BCDE内部,
∴∠ADE=∠A′DE,∠AED=∠A′ED,
∴2∠ADE=180°﹣∠1,2∠AED=180°﹣∠2,
∴∠ADE=90°﹣∠1,∠AED=90°﹣∠2,
∵在△ADE中,∠A=180°﹣(∠AED+∠ADE),
∴∠A=∠1+∠2,
即2∠A=∠1+∠2.
【点评】本题考查了折叠的性质和三角形的内角和定理的应用,关键是得出等式∠ADE=90°﹣∠1,∠AED=90°﹣∠2,∠A=180°﹣(∠AED+∠ADE).
23.(1)见解析
(2)
【分析】本题考查角平分线的定义,三角形全等的判定与性质,三角形三边关系,正确作出辅助线构造三角形全等是解题的关键.
(1)在上取点E,使得,证明得到,由得到,根据三角形三边关系得到,即可证明结论;
(2)延长到点F,使得,连接,证明,得到,在中,利用三角形三边关系即可求解.
【详解】(1)证明:如图,在上取点E,使得,在与中,
平分,
,
,
,
,
,
,
,
;
(2)解:延长到点F,使得,连接,
,
,
为边上的中线,
,
,
,
,
,
在中,,
.
24.(1),,
(2)
【分析】(1)利用三角形的一条中线把三角形的面积分成相等的两部分求解即可;
(2)根据(1)中的求解可得规律,利用规律即可求解.
【详解】(1)解:∵是的边BC上的中线,的面积为S,如图1,
∴;
又∵是的边上的中线,如图2,
∴;
∵是的边上的中线,如图3,
∴,
故答案为:,,
(2)解:∵,
,
,
,
以此类推,
可得,
∴当时,,
故答案为:
