2.3 一元二次方程根的判别式 课件(共14张PPT)
文档属性
| 名称 | 2.3 一元二次方程根的判别式 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 11:27:47 | ||
图片预览






文档简介
(共15张PPT)
2.3 一元二次方程根的判别式
我们在运用公式法解一元二次方程 ax2+bx+c=0(a≠0)时,总是要求b2-4ac≥0.这是为什么?
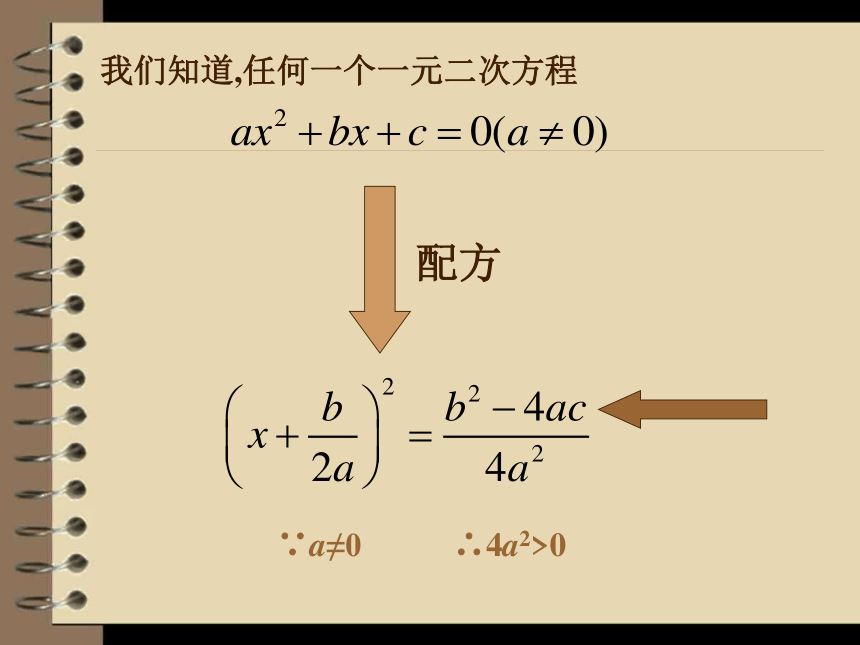
我们知道,任何一个一元二次方程
∵a≠0
∴4a2>0
配方
∵a≠0 ∴4a2>0
当 时,
当 时,
当 时,
方程有两个不相等的实数根:
方程有两个相等的实数根:
方程没有实数根.
1.
3.
2.
我们把 叫做一元二次方程
的根的判别式,
用符号“ ”表示,即 .
记住了,别搞错!
结论
1.当 时,方程有两个不相等的实数根,其根为:
一元二次方程: 的根的情况可由 来判断:
2.当 时,方程有两个相等的实数根,其根为:
3.当 时,方程有没有实数根.
x1= ,x2= ;
x1=x2= ;
例题讲解
例 不解方程,利用判别式判断下列方程根的情况.
(1) 3x2-x+1 = 3x ;
(2) 5(x2+1)= 7x ;
(3) x2-4x = -4 .
方程要先化为一般形式,再求判别式
解:(1)原方程化为一般形式为:
3x2-4x+1 = 0 .
因为 =(-4)2-4×3×1
=16-12=4>0,
所以,原方程有两个不相等的实数根.
解:(2)原方程化为一般形式为:
5x2-7x+5 = 0 .
因为 =(-7)2-4×5×5
=49-100=-51<0,
所以,原方程没有实数根.
解:(3)原方程化为一般形式为:
x2-4x+4 = 0 .
因为 =(-4)2-4×1×4
=16-16=0,
所以,原方程有两个相等的实数根.
(1)今天我们是在一元二次方程解法的基础上,学习了根的判别式的应用,它在整个中学数学中占有重要地位,是中考命题的重要知识点,所以必须牢固掌握好它。
(2)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(3)一元二次方程aX2+bx+c=0(a≠0)(△=b2-4ac)
判别式
情况
根 的 情 况
定 理 与 逆 定 理
△>0
X1,X2=
△≥0<=>有(两个)实数根
△>0<=>有两个不等实数根
△=0
X1,X2=
△=0<=>有两个相等实数根
△<0
无意义, X1,X2不存在
△<0<=>无实根
1.一元二次方程x2+2x+4=0的根的情况是 ( )
A.有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
D
2.方程x2-3x+1=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C. 没有实数根 D.只有一个实数根
A
3.下列一元一次方程中,有实数根的是 ( )
A.x2-x+1=0 B.x2-2x+3=0
C.x2+x-1=0 D.x2+4=0
C
练习
练习
4.若方程 2x2-(k-1)x+8=0 有两个相等的实数根,求k的值.
解:
又∵方程有两个相等的实数根,
2.3 一元二次方程根的判别式
我们在运用公式法解一元二次方程 ax2+bx+c=0(a≠0)时,总是要求b2-4ac≥0.这是为什么?
我们知道,任何一个一元二次方程
∵a≠0
∴4a2>0
配方
∵a≠0 ∴4a2>0
当 时,
当 时,
当 时,
方程有两个不相等的实数根:
方程有两个相等的实数根:
方程没有实数根.
1.
3.
2.
我们把 叫做一元二次方程
的根的判别式,
用符号“ ”表示,即 .
记住了,别搞错!
结论
1.当 时,方程有两个不相等的实数根,其根为:
一元二次方程: 的根的情况可由 来判断:
2.当 时,方程有两个相等的实数根,其根为:
3.当 时,方程有没有实数根.
x1= ,x2= ;
x1=x2= ;
例题讲解
例 不解方程,利用判别式判断下列方程根的情况.
(1) 3x2-x+1 = 3x ;
(2) 5(x2+1)= 7x ;
(3) x2-4x = -4 .
方程要先化为一般形式,再求判别式
解:(1)原方程化为一般形式为:
3x2-4x+1 = 0 .
因为 =(-4)2-4×3×1
=16-12=4>0,
所以,原方程有两个不相等的实数根.
解:(2)原方程化为一般形式为:
5x2-7x+5 = 0 .
因为 =(-7)2-4×5×5
=49-100=-51<0,
所以,原方程没有实数根.
解:(3)原方程化为一般形式为:
x2-4x+4 = 0 .
因为 =(-4)2-4×1×4
=16-16=0,
所以,原方程有两个相等的实数根.
(1)今天我们是在一元二次方程解法的基础上,学习了根的判别式的应用,它在整个中学数学中占有重要地位,是中考命题的重要知识点,所以必须牢固掌握好它。
(2)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(3)一元二次方程aX2+bx+c=0(a≠0)(△=b2-4ac)
判别式
情况
根 的 情 况
定 理 与 逆 定 理
△>0
X1,X2=
△≥0<=>有(两个)实数根
△>0<=>有两个不等实数根
△=0
X1,X2=
△=0<=>有两个相等实数根
△<0
无意义, X1,X2不存在
△<0<=>无实根
1.一元二次方程x2+2x+4=0的根的情况是 ( )
A.有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
D
2.方程x2-3x+1=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C. 没有实数根 D.只有一个实数根
A
3.下列一元一次方程中,有实数根的是 ( )
A.x2-x+1=0 B.x2-2x+3=0
C.x2+x-1=0 D.x2+4=0
C
练习
练习
4.若方程 2x2-(k-1)x+8=0 有两个相等的实数根,求k的值.
解:
又∵方程有两个相等的实数根,
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
