10.1 电势能和电势 (共23张PPT) 课件 2024-2025学年高一物理人教版(2019)必修第三册
文档属性
| 名称 | 10.1 电势能和电势 (共23张PPT) 课件 2024-2025学年高一物理人教版(2019)必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-25 13:50:10 | ||
图片预览







文档简介
(共23张PPT)
第十章 静电场中的能量
第1节 电势能和电势
问题:一个带正电的试探电荷在匀强电场中某点由静止释放,若只受静电力作用,将如何运动 动能如何变化?
E
在电场力作用下电荷加速运动,试探电荷的动能增加.
+
F
思考:是什么能转化为试探电荷的动能呢
1.通过计算在匀强电场中移动电荷静电力所做的功,认识静电力做功与路径无关的特点。
2.了解电荷在电场中的电势能,知道静电力做功与电势能变化的关系。
3.知道电势的定义方法及其公式、单位,会判断电场中两点电势的高低。
知识点一:静电力做功的特点
M
E
W = qE·|AB| cosθ
= qE·|AM|
1.将电荷q从A沿直线移至B
A
B
θ
+
q
F
2.将电荷q从A沿折线移至B
W1 = qE ·|AM|
W2 = 0
W = W1 + W2= qE·|AM|
M
θ
E
A
B
+
q
F
M
θ
E
A
B
+
q
F
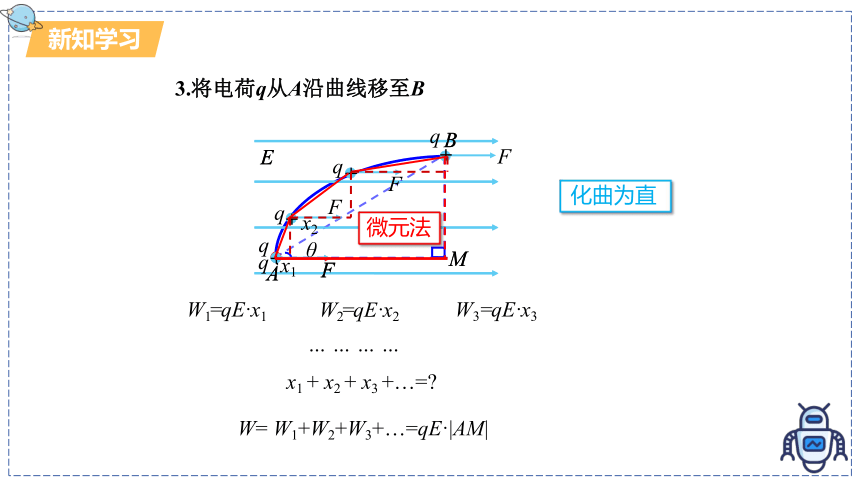
3.将电荷q从A沿曲线移至B
E
A
B
+
q
F
+
q
F
+
q
F
+
q
F
M
x1
x2
微元法
W= W1+W2+W3+…=qE·|AM|
W1=qE·x1
W2=qE·x2
W3 =qE·x3
… … … …
x1 + x2 + x3 +…=
化曲为直
在匀强电场中移动电荷时,静电力的功与电荷的起始位置和终止位置有关,但与电荷经过的路径无关。
此结论对于非匀强电场也适用
这与什么力做功相似呢?
沿任意路径静电力做功:
W任意 = qE·|AM|
W任意 =qELcos θ (θ为力与位移之间的夹角)
mg
qE
重力做功
类比
电场做功
功和能量的变化密切相关。重力做功对应着重力势能的变化,那么,静电力做功又对应着哪种形式的能量变化呢?
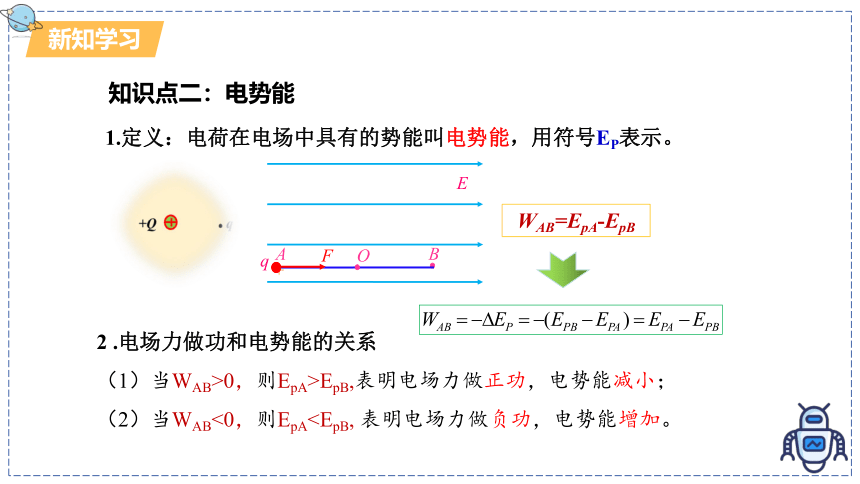
知识点二:电势能
2 .电场力做功和电势能的关系
(1)当WAB>0,则EpA>EpB,表明电场力做正功,电势能减小;
(2)当WAB<0,则EpAWAB=EpA-EpB
E
A
B
+
q
F
O
1.定义:电荷在电场中具有的势能叫电势能,用符号EP表示。
3.电势能是相对的,具体数值与零势能面的选取有关;
4.电势能为电荷和对它作用的电场组成的系统共有。
5.电势能是标量。
通常把电荷在离场源电荷无限远处的电势能规定为0,或把电荷在大地表面的电势能规定为0。
多远算“无限远” 呢?
q
Q
我们说某个电荷的电势能,只是一种简略的说法。
1.电荷在某点的电势能,等于把它从该点移动到零势能面时静电力所做的功。
E
A
B
若以A点作为零势能面,
则有 EPA-EPB=WAB
因EPA=0 ,则 EPB= -WAB
如图,若A→B电场力所做功为WAB
若以B点作为零势能面,
则EPA-0=WAB即EPA=WAB
2.选择不同的零势能面,对于同一个带电体在同一点来说电势能大小是不相同的。
6.电势能的大小:
总结:
思考:电场的力的性质我们用场强E来描述,那么电场的能的性质我们又应该用什么物理量来描述呢?能否用“电势能”呢?
A
O
L
θ
E
+
如图:有一个电场强度为E的匀强电场,规定电荷在O点的电势能为0。A为电场中的任意一点。用图中已知量表示出正电荷q在A点的电势能。
q
EpA=WAO=qELcosθ
思考:通过表格中的数据发现这个功与电荷的多少有关,但是不能用它来表示电场某点的性质。那么用什么物理量来反映电场某点性质呢?
通过分析可知,至于A点的电荷,如果它的电荷变为原来的几倍,其电势能也变为原来的几倍,电势能与电荷量之比却是一定的。
常量与EP及q无关,即与试验电荷无关,反映电场本身的某种性质;
EpA=WAO=qELcosθ
1.定义: 电荷在电场中某一点的电势能与它的电荷量之比,叫做电场在这一点的电势,用φ表示。
2.定义式:
(计算时EP和q要代入正负号)
3.物理意义:反映电场能的性质,由电场本身的性质决定的,与是否引入电荷,以及引入电荷的电性和电量无关。
4.单位:伏特,符号为V 1 V = 1 J/C
知识点三:电势
6.电势是标量(有正负),正值表示该点电势比零高,负值表示该点电势比零低。
5.电势具有相对性
类比
电势
高度
电势能
重力势能
确定电势,应先规定电场中某处的电势为零。(一般选取无穷远处或大地电势为0)
1.假如正试探电荷沿着电场线从A点移到B点,电荷的电势能如何变化
A、B两点电势有什么关系
电场力做正功、电势能减少 φA>φB
2.假如负试探电荷从A点移到B点,电势能如何变化 A、B两点电势有
什么关系
电场力做负功、电势能增加 φA>φB
电势高低的判断方法
1.电场线法:沿着电场线方向电势逐渐降低。
2.场源电荷法:离场源正电荷越近的点,电势越高;离场源负电荷越近的点,电势越低。
3.公式法:由φ=知,对于同一正电荷,电势能越大,所在位置的电势越高;对于同一负电荷,电势能越小,所在位置的电势越高。
1.如图所示是以电荷+Q为圆心的一组同心圆(虚线),电场中有A、B、C、D四点。现将一带电荷量为q的正点电荷由A点沿不同的路径移动到D点,沿路径①做功为W1,沿路径②做功为W2,沿路径③做功为W3,则( )
A.W2C.W2>W3>W1 D.W3>W2>W1
B
2.如图所示的电场中有A、B两点,下列判断正确的是( )
A.电势关系为φA>φB,电场强度大小关系为EA>EB
B.电势关系为φA<φB,电场强度大小关系为EAC.将电荷量为q的正电荷从A点移到B点,静电力做负功,电势能增加
D.将电荷量为q的负电荷分别放在A、B两点,电荷具有的电势能关系为EpAD
3.某静电场的电场线分布如图所示,图中A、B两点的电场强度大小分别为EA和EB,电势分别为φA和φB,将带电量为q的负电荷分别放在A、B两点时具有的电势能分别为EpA和EpB,则有( )
A. EA>EB,φA>φB,EpAB. EA>EB,φA>φB,EpA>EpB
C. EAφB,EpA>EpB
D. EAA
4.将带电荷量为6×10-6 C的负电荷从电场中的A点移到B点,克服静电力做了3×10-5 J的功,再从B移到C,静电力做了1.2×10-5 J的功,则:
(1)电荷从A移到B,再从B移到C的过程中电势能
改变了多少
(2)如果规定A点的电势能为零,则该电荷在B点和C点的电势能分别为多少
(3)如果规定B点的电势能为零,则该电荷在A点和C点的电势能分别为多少
解:(1)静电力先做负功后做正功,则电荷从A经B到C的过程中,静电力做功WAC=WAB+WBC=(-3×10-5+1.2×10-5) J=-1.8×10-5 J,则知电势能增加了1.8×10-5 J。
(2)若A点的电势能为零,则B点的电势能为EpB=EpA-WAB=0-WAB=3×10-5 J,同理,C点的电势能为EpC=EpA-WAC=0-WAC=1.8×10-5 J。
(3)若B点的电势能为零,则该电荷在A点的电势能为EpA'=EpB'+WAB=0+WAB=-3×10-5 J
C点的电势能为EpC'=EpB'-WBC=0-WBC=-1.2×10-5 J。
5.如图,将q1=2×10-6 C的试探电荷从A点移到B点,静电力做功5×10-5 J,从B点移到无穷远处,静电力做功8×10-5 J。以无穷远处的电势为零,求:
(1)电荷q1在A、B两点的电势能;
答案 (1) 1.3×10-4 J 8×10-5 J
(2) 65 V 40 V (3) -1.3×10-4 J -8×10-5 J
(2)A、B两点的电势;
(3)q2=-2×10-6 C的电荷在A、B两点的电势能。
第十章 静电场中的能量
第1节 电势能和电势
问题:一个带正电的试探电荷在匀强电场中某点由静止释放,若只受静电力作用,将如何运动 动能如何变化?
E
在电场力作用下电荷加速运动,试探电荷的动能增加.
+
F
思考:是什么能转化为试探电荷的动能呢
1.通过计算在匀强电场中移动电荷静电力所做的功,认识静电力做功与路径无关的特点。
2.了解电荷在电场中的电势能,知道静电力做功与电势能变化的关系。
3.知道电势的定义方法及其公式、单位,会判断电场中两点电势的高低。
知识点一:静电力做功的特点
M
E
W = qE·|AB| cosθ
= qE·|AM|
1.将电荷q从A沿直线移至B
A
B
θ
+
q
F
2.将电荷q从A沿折线移至B
W1 = qE ·|AM|
W2 = 0
W = W1 + W2= qE·|AM|
M
θ
E
A
B
+
q
F
M
θ
E
A
B
+
q
F
3.将电荷q从A沿曲线移至B
E
A
B
+
q
F
+
q
F
+
q
F
+
q
F
M
x1
x2
微元法
W= W1+W2+W3+…=qE·|AM|
W1=qE·x1
W2=qE·x2
W3 =qE·x3
… … … …
x1 + x2 + x3 +…=
化曲为直
在匀强电场中移动电荷时,静电力的功与电荷的起始位置和终止位置有关,但与电荷经过的路径无关。
此结论对于非匀强电场也适用
这与什么力做功相似呢?
沿任意路径静电力做功:
W任意 = qE·|AM|
W任意 =qELcos θ (θ为力与位移之间的夹角)
mg
qE
重力做功
类比
电场做功
功和能量的变化密切相关。重力做功对应着重力势能的变化,那么,静电力做功又对应着哪种形式的能量变化呢?
知识点二:电势能
2 .电场力做功和电势能的关系
(1)当WAB>0,则EpA>EpB,表明电场力做正功,电势能减小;
(2)当WAB<0,则EpA
E
A
B
+
q
F
O
1.定义:电荷在电场中具有的势能叫电势能,用符号EP表示。
3.电势能是相对的,具体数值与零势能面的选取有关;
4.电势能为电荷和对它作用的电场组成的系统共有。
5.电势能是标量。
通常把电荷在离场源电荷无限远处的电势能规定为0,或把电荷在大地表面的电势能规定为0。
多远算“无限远” 呢?
q
Q
我们说某个电荷的电势能,只是一种简略的说法。
1.电荷在某点的电势能,等于把它从该点移动到零势能面时静电力所做的功。
E
A
B
若以A点作为零势能面,
则有 EPA-EPB=WAB
因EPA=0 ,则 EPB= -WAB
如图,若A→B电场力所做功为WAB
若以B点作为零势能面,
则EPA-0=WAB即EPA=WAB
2.选择不同的零势能面,对于同一个带电体在同一点来说电势能大小是不相同的。
6.电势能的大小:
总结:
思考:电场的力的性质我们用场强E来描述,那么电场的能的性质我们又应该用什么物理量来描述呢?能否用“电势能”呢?
A
O
L
θ
E
+
如图:有一个电场强度为E的匀强电场,规定电荷在O点的电势能为0。A为电场中的任意一点。用图中已知量表示出正电荷q在A点的电势能。
q
EpA=WAO=qELcosθ
思考:通过表格中的数据发现这个功与电荷的多少有关,但是不能用它来表示电场某点的性质。那么用什么物理量来反映电场某点性质呢?
通过分析可知,至于A点的电荷,如果它的电荷变为原来的几倍,其电势能也变为原来的几倍,电势能与电荷量之比却是一定的。
常量与EP及q无关,即与试验电荷无关,反映电场本身的某种性质;
EpA=WAO=qELcosθ
1.定义: 电荷在电场中某一点的电势能与它的电荷量之比,叫做电场在这一点的电势,用φ表示。
2.定义式:
(计算时EP和q要代入正负号)
3.物理意义:反映电场能的性质,由电场本身的性质决定的,与是否引入电荷,以及引入电荷的电性和电量无关。
4.单位:伏特,符号为V 1 V = 1 J/C
知识点三:电势
6.电势是标量(有正负),正值表示该点电势比零高,负值表示该点电势比零低。
5.电势具有相对性
类比
电势
高度
电势能
重力势能
确定电势,应先规定电场中某处的电势为零。(一般选取无穷远处或大地电势为0)
1.假如正试探电荷沿着电场线从A点移到B点,电荷的电势能如何变化
A、B两点电势有什么关系
电场力做正功、电势能减少 φA>φB
2.假如负试探电荷从A点移到B点,电势能如何变化 A、B两点电势有
什么关系
电场力做负功、电势能增加 φA>φB
电势高低的判断方法
1.电场线法:沿着电场线方向电势逐渐降低。
2.场源电荷法:离场源正电荷越近的点,电势越高;离场源负电荷越近的点,电势越低。
3.公式法:由φ=知,对于同一正电荷,电势能越大,所在位置的电势越高;对于同一负电荷,电势能越小,所在位置的电势越高。
1.如图所示是以电荷+Q为圆心的一组同心圆(虚线),电场中有A、B、C、D四点。现将一带电荷量为q的正点电荷由A点沿不同的路径移动到D点,沿路径①做功为W1,沿路径②做功为W2,沿路径③做功为W3,则( )
A.W2
B
2.如图所示的电场中有A、B两点,下列判断正确的是( )
A.电势关系为φA>φB,电场强度大小关系为EA>EB
B.电势关系为φA<φB,电场强度大小关系为EA
D.将电荷量为q的负电荷分别放在A、B两点,电荷具有的电势能关系为EpA
3.某静电场的电场线分布如图所示,图中A、B两点的电场强度大小分别为EA和EB,电势分别为φA和φB,将带电量为q的负电荷分别放在A、B两点时具有的电势能分别为EpA和EpB,则有( )
A. EA>EB,φA>φB,EpA
C. EA
D. EA
4.将带电荷量为6×10-6 C的负电荷从电场中的A点移到B点,克服静电力做了3×10-5 J的功,再从B移到C,静电力做了1.2×10-5 J的功,则:
(1)电荷从A移到B,再从B移到C的过程中电势能
改变了多少
(2)如果规定A点的电势能为零,则该电荷在B点和C点的电势能分别为多少
(3)如果规定B点的电势能为零,则该电荷在A点和C点的电势能分别为多少
解:(1)静电力先做负功后做正功,则电荷从A经B到C的过程中,静电力做功WAC=WAB+WBC=(-3×10-5+1.2×10-5) J=-1.8×10-5 J,则知电势能增加了1.8×10-5 J。
(2)若A点的电势能为零,则B点的电势能为EpB=EpA-WAB=0-WAB=3×10-5 J,同理,C点的电势能为EpC=EpA-WAC=0-WAC=1.8×10-5 J。
(3)若B点的电势能为零,则该电荷在A点的电势能为EpA'=EpB'+WAB=0+WAB=-3×10-5 J
C点的电势能为EpC'=EpB'-WBC=0-WBC=-1.2×10-5 J。
5.如图,将q1=2×10-6 C的试探电荷从A点移到B点,静电力做功5×10-5 J,从B点移到无穷远处,静电力做功8×10-5 J。以无穷远处的电势为零,求:
(1)电荷q1在A、B两点的电势能;
答案 (1) 1.3×10-4 J 8×10-5 J
(2) 65 V 40 V (3) -1.3×10-4 J -8×10-5 J
(2)A、B两点的电势;
(3)q2=-2×10-6 C的电荷在A、B两点的电势能。
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
