人教版五年级数学上册《简易方程》(课件)(共25张PPT)
文档属性
| 名称 | 人教版五年级数学上册《简易方程》(课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 459.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
人教版五年级上册
《简易方程》
整理和复习
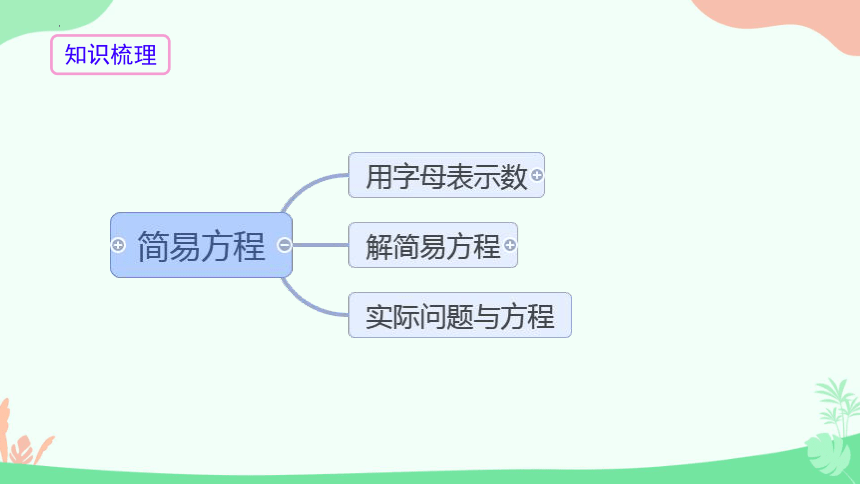
知识梳理
第一模块:用字母表示数
知识点1: 用字母表示数、数量关系
知识点2: 用字母表示运算定律和计算公式
知识点3: 用字母表示稍复杂的数量关系
用含有字母的式子表示下面的数量关系。
(1)比a的6倍少8。 ( )
(2)从96里连续减去6个a。( )
(3)a与b的和除以它们的差。( )
6a-8
96-6a
(a+b) ÷(a-b)
对点训练
知识点2:用字母表示运算定律和计算公式
加法交换律 a+b=b+a
加法结合律 (a+b)+c=a+(b+c)
乘法交换律 ab=ba
乘法结合律 (ab)c=a(bc)
乘法分配律 (a+b)c=ac+bc
如果用S表示面积,用C表示周长,用a表示正方形的边长
用字母表示计算公式:
S=a.a
=a
正方形面积:
正方形周长:
C=4a
如果用S表示面积,用a表示底,用h表示高。
平行四边形面积:S=ah
三角形面积:S=ah÷2
如果用S表示面积,用a表示上底,用b表示下底,用h表示高。
梯形面积:S=(a+b)h÷2
根据运算定律在 里填上适当的数或字母。
(1)(a+54)+46= +( + )
(2)6a+5a=( + ).a
(3)a-b-c= -( + )
(4)(a+28)×b= × + ×
a
54
46
6
5
a
b
c
a
b
b
28
对点训练
知识点3: 用字母表示稍复杂的数量关系
水果批发城运来a车苹果,每车装180箱,b天卖完。
(1)用含有字母的式子表示平均每天卖出多少箱。
(2)当a=4,b=9时,平均每天卖出多少箱?
苹果总量÷天数=平均每天卖出的箱数
180a
÷
=180×4÷9
=720÷9
=80(箱)
b
(1)
(2)
180a÷b
第二模块: 解简易方程
知识点1: 方程的意义
知识点2: 等式的性质
知识点3: 解方程
含有未知数的等式就是方程。
方程的定义:
判断题
1.含有未知数的式子叫方程。 ( )
2.a+x=b 是方程。 ( )
3.等式一定是方程,而有的方程不一定是等式。 ( )
4.6x-18=0和4x-18中都含有未知数,所以都是方程 ( )
√
×
×
×
知识点1: 方程的意义
对点训练
知识点2: 等式的性质
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
知识点3: 解方程
利用等式的性质来解方程。
类型1:形如x±a=b的方程的解法
检验:把x=21代入原方程
方程左边=x +15
=21+15
=36
所以,x=6是方程的解。
解:
x +15=36
x +15-15=36-15
x=21
=方程右边
类型2:形如ax=b和x÷a=b(a≠0)的方程的解法
x÷9=0.7
解:x ÷9×9=0.7×9
x=6.3
2.4x =0.96
检验:把x =6.3代入原方程
方程左边=x÷9
=6.3÷9
=0.7
=方程右边,
所以,x =6.3是方程的解。
类型3:形如a-x=b和a÷x=b 的方程的解法
3.8-x=1.2
275÷x=100
解:3.8-x+x=1.2+x
解:275÷x×x=100×x
3.8=1.2+x
275=100x
1.2+x=3.8
100x=275
1.2+x-1.2=3.8-1.2
x=2.6
100x÷100=275÷100
x=2.75
(先把ax看成一个整体,
求出ax的值,再求x的值)
类型4:形如ax±b=c的方程的解法
6x-7.3=19.7
解:6x-7.3+7.3=19.7+7.3
6x=27
6x÷6=27÷6
x =4.5
变式练习:
0.7x+ =37
+7=37
解:0.7x+30=37
解:5x+7=37
0.7x+30-30=37-30
5x+7-7=37-7
0.7x=7
5x=30
0.7x÷0.7=7÷0.7
5x÷5=30÷5
x=10
x=6
6×5
6×5
3x+2x
3x+2x
类型5:形如a(x±b)=c的方程的解法 (两种解法)
方法二:利用乘法分配率,先把括号去掉,再利用等式的性质分步求解。
方法一:把(x±b)看成一个整体,先求出(x±b)的值,再求出x的值。
2(x-2.8)=10.4
2(x-2.8)=10.4
解:2(x-2.8)÷2=10.4÷2
解:2x-2×2.8=10.4
x-2.8=5.2
2x-5.6=10.4
x-2.8+2.8=5.2+2.8
2x-5.6+5.6=10.4+5.6
x=8
2x=16
2x÷2=16÷2
x=8
列方程解决实际问题的步骤:
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,列方程;
(3)解方程并检验作答。
第三模块:实际问题与方程
一件衣服现价178元,比原来降低了121元,这件衣服原价多少钱?
类型1:列形如x±a=b的方程解决实际问题
解:设这件衣服原价x元
x-121=178
x-121+121=178+121
x=299
x-178=121
x-178+178=121+178
x=299
原价-降低的钱数=现价
答:这件衣服299元。
原价-现价=降低的钱数
类型2:列形如ax±b=c的方程解决实际问题(求一个数比另一个数的几倍多(少)几的问题)
果园里有157棵梨树,比苹果树的3倍多16棵。苹果树有多少棵?
类型3:列形如ax±bc=d的方程解决实际问题
小明去书店买书,他带了75元钱,其中3张面值为5元的人民币,剩下的是面值为10元的人民币,10元的面值有多少张?
解:设10元面值的有x张
10x+3×5=75
10元面值的总金额 + 5元面值的总金额= 75元
10x+15=75
10x+15=75-15
10x=60
x=6
答:10元的面值有6张。
(含有两个未知数时,一般设1倍量为x,另一个未知数用含有x的式子表示出来,再根据两数之和或两数之差来列方程)
类型4:列方程解决“和倍”“差倍”问题
小明和小红共有126张邮票,小红的邮票数是小明的2倍,小明和小红各有多少张邮票?
解:设小明有x张邮票,那么小红有2x张邮票。
x+2x=126
3x=126
3x÷3=126÷3
x=42
小红:
方法1:2x=42×2=84(张)
小明的邮票数 + 小红的邮票数 = 126
方法2:126-42=84(张)
答:小明有42张邮票,小红有84张邮票
志明和小宁同时从相距530m的两地相向而行,经过5分钟相遇。小宁每分钟走多少米
解:设小宁每分钟走x米。
志明走的路程+小宁走的路程=总路程
54×5+5x=530
(志明和小宁每分钟走的路程和)×时间=总路程
(54+x)×5=530
类型5:列方程解决行程问题
列方程解决实际问题类型
类型1:列形如x±a=b的方程解决实际问题
类型2:列形如ax±b=c的方程解决实际问题(求一个数比另一个
数的几倍多(少)几的问题)
类型3:列形如ax±bc=d的方程解决实际问题
类型4:列方程解决“和倍”“差倍”问题
类型5:列方程解决行程问题
回顾总结
(12-2x)÷2=3
1.解方程:
2.列方程解决问题
(1)弟弟有22元,哥哥有152元,哥哥给弟弟多少元后, 哥哥的钱是弟弟的2倍?
(2)陈老师到新华书店一共买了10本《语文阅读》和《趣味数学》, 共用去77元,每本《语文阅读》8元,每本《趣味数学》7元,
陈老师两种书各买了多少本?
(3)甲、乙两城相距315km,一辆汽车由甲城开往乙城,一辆摩托车由乙城开往甲城。汽车每小时行驶60km,3小时后两车相距15km。摩托车每小时行驶多少千米?
课后作业
人教版五年级上册
《简易方程》
整理和复习
知识梳理
第一模块:用字母表示数
知识点1: 用字母表示数、数量关系
知识点2: 用字母表示运算定律和计算公式
知识点3: 用字母表示稍复杂的数量关系
用含有字母的式子表示下面的数量关系。
(1)比a的6倍少8。 ( )
(2)从96里连续减去6个a。( )
(3)a与b的和除以它们的差。( )
6a-8
96-6a
(a+b) ÷(a-b)
对点训练
知识点2:用字母表示运算定律和计算公式
加法交换律 a+b=b+a
加法结合律 (a+b)+c=a+(b+c)
乘法交换律 ab=ba
乘法结合律 (ab)c=a(bc)
乘法分配律 (a+b)c=ac+bc
如果用S表示面积,用C表示周长,用a表示正方形的边长
用字母表示计算公式:
S=a.a
=a
正方形面积:
正方形周长:
C=4a
如果用S表示面积,用a表示底,用h表示高。
平行四边形面积:S=ah
三角形面积:S=ah÷2
如果用S表示面积,用a表示上底,用b表示下底,用h表示高。
梯形面积:S=(a+b)h÷2
根据运算定律在 里填上适当的数或字母。
(1)(a+54)+46= +( + )
(2)6a+5a=( + ).a
(3)a-b-c= -( + )
(4)(a+28)×b= × + ×
a
54
46
6
5
a
b
c
a
b
b
28
对点训练
知识点3: 用字母表示稍复杂的数量关系
水果批发城运来a车苹果,每车装180箱,b天卖完。
(1)用含有字母的式子表示平均每天卖出多少箱。
(2)当a=4,b=9时,平均每天卖出多少箱?
苹果总量÷天数=平均每天卖出的箱数
180a
÷
=180×4÷9
=720÷9
=80(箱)
b
(1)
(2)
180a÷b
第二模块: 解简易方程
知识点1: 方程的意义
知识点2: 等式的性质
知识点3: 解方程
含有未知数的等式就是方程。
方程的定义:
判断题
1.含有未知数的式子叫方程。 ( )
2.a+x=b 是方程。 ( )
3.等式一定是方程,而有的方程不一定是等式。 ( )
4.6x-18=0和4x-18中都含有未知数,所以都是方程 ( )
√
×
×
×
知识点1: 方程的意义
对点训练
知识点2: 等式的性质
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
知识点3: 解方程
利用等式的性质来解方程。
类型1:形如x±a=b的方程的解法
检验:把x=21代入原方程
方程左边=x +15
=21+15
=36
所以,x=6是方程的解。
解:
x +15=36
x +15-15=36-15
x=21
=方程右边
类型2:形如ax=b和x÷a=b(a≠0)的方程的解法
x÷9=0.7
解:x ÷9×9=0.7×9
x=6.3
2.4x =0.96
检验:把x =6.3代入原方程
方程左边=x÷9
=6.3÷9
=0.7
=方程右边,
所以,x =6.3是方程的解。
类型3:形如a-x=b和a÷x=b 的方程的解法
3.8-x=1.2
275÷x=100
解:3.8-x+x=1.2+x
解:275÷x×x=100×x
3.8=1.2+x
275=100x
1.2+x=3.8
100x=275
1.2+x-1.2=3.8-1.2
x=2.6
100x÷100=275÷100
x=2.75
(先把ax看成一个整体,
求出ax的值,再求x的值)
类型4:形如ax±b=c的方程的解法
6x-7.3=19.7
解:6x-7.3+7.3=19.7+7.3
6x=27
6x÷6=27÷6
x =4.5
变式练习:
0.7x+ =37
+7=37
解:0.7x+30=37
解:5x+7=37
0.7x+30-30=37-30
5x+7-7=37-7
0.7x=7
5x=30
0.7x÷0.7=7÷0.7
5x÷5=30÷5
x=10
x=6
6×5
6×5
3x+2x
3x+2x
类型5:形如a(x±b)=c的方程的解法 (两种解法)
方法二:利用乘法分配率,先把括号去掉,再利用等式的性质分步求解。
方法一:把(x±b)看成一个整体,先求出(x±b)的值,再求出x的值。
2(x-2.8)=10.4
2(x-2.8)=10.4
解:2(x-2.8)÷2=10.4÷2
解:2x-2×2.8=10.4
x-2.8=5.2
2x-5.6=10.4
x-2.8+2.8=5.2+2.8
2x-5.6+5.6=10.4+5.6
x=8
2x=16
2x÷2=16÷2
x=8
列方程解决实际问题的步骤:
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,列方程;
(3)解方程并检验作答。
第三模块:实际问题与方程
一件衣服现价178元,比原来降低了121元,这件衣服原价多少钱?
类型1:列形如x±a=b的方程解决实际问题
解:设这件衣服原价x元
x-121=178
x-121+121=178+121
x=299
x-178=121
x-178+178=121+178
x=299
原价-降低的钱数=现价
答:这件衣服299元。
原价-现价=降低的钱数
类型2:列形如ax±b=c的方程解决实际问题(求一个数比另一个数的几倍多(少)几的问题)
果园里有157棵梨树,比苹果树的3倍多16棵。苹果树有多少棵?
类型3:列形如ax±bc=d的方程解决实际问题
小明去书店买书,他带了75元钱,其中3张面值为5元的人民币,剩下的是面值为10元的人民币,10元的面值有多少张?
解:设10元面值的有x张
10x+3×5=75
10元面值的总金额 + 5元面值的总金额= 75元
10x+15=75
10x+15=75-15
10x=60
x=6
答:10元的面值有6张。
(含有两个未知数时,一般设1倍量为x,另一个未知数用含有x的式子表示出来,再根据两数之和或两数之差来列方程)
类型4:列方程解决“和倍”“差倍”问题
小明和小红共有126张邮票,小红的邮票数是小明的2倍,小明和小红各有多少张邮票?
解:设小明有x张邮票,那么小红有2x张邮票。
x+2x=126
3x=126
3x÷3=126÷3
x=42
小红:
方法1:2x=42×2=84(张)
小明的邮票数 + 小红的邮票数 = 126
方法2:126-42=84(张)
答:小明有42张邮票,小红有84张邮票
志明和小宁同时从相距530m的两地相向而行,经过5分钟相遇。小宁每分钟走多少米
解:设小宁每分钟走x米。
志明走的路程+小宁走的路程=总路程
54×5+5x=530
(志明和小宁每分钟走的路程和)×时间=总路程
(54+x)×5=530
类型5:列方程解决行程问题
列方程解决实际问题类型
类型1:列形如x±a=b的方程解决实际问题
类型2:列形如ax±b=c的方程解决实际问题(求一个数比另一个
数的几倍多(少)几的问题)
类型3:列形如ax±bc=d的方程解决实际问题
类型4:列方程解决“和倍”“差倍”问题
类型5:列方程解决行程问题
回顾总结
(12-2x)÷2=3
1.解方程:
2.列方程解决问题
(1)弟弟有22元,哥哥有152元,哥哥给弟弟多少元后, 哥哥的钱是弟弟的2倍?
(2)陈老师到新华书店一共买了10本《语文阅读》和《趣味数学》, 共用去77元,每本《语文阅读》8元,每本《趣味数学》7元,
陈老师两种书各买了多少本?
(3)甲、乙两城相距315km,一辆汽车由甲城开往乙城,一辆摩托车由乙城开往甲城。汽车每小时行驶60km,3小时后两车相距15km。摩托车每小时行驶多少千米?
课后作业
