11.2.2三角形的外角优化练(2)(含解析)2024--2025学年初中数学人教版八年级上册
文档属性
| 名称 | 11.2.2三角形的外角优化练(2)(含解析)2024--2025学年初中数学人教版八年级上册 | 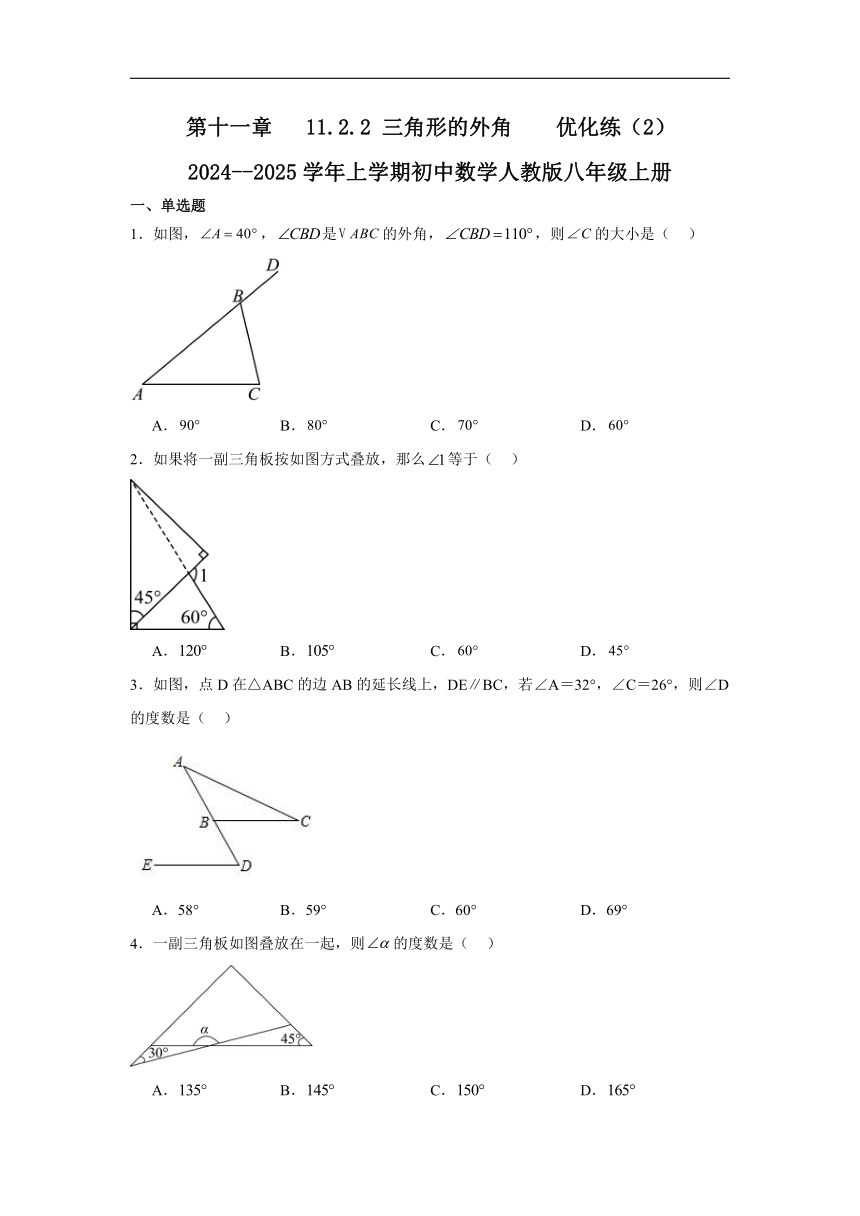 | |
| 格式 | docx | ||
| 文件大小 | 668.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 23:04:10 | ||
图片预览




文档简介
第十一章 11.2.2 三角形的外角 优化练(2) 2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.如图,,是的外角,,则的大小是( )
A. B. C. D.
2.如果将一副三角板按如图方式叠放,那么等于( )
A. B. C. D.
3.如图,点D在△ABC的边AB的延长线上,DE∥BC,若∠A=32°,∠C=26°,则∠D的度数是( )
A.58° B.59° C.60° D.69°
4.一副三角板如图叠放在一起,则的度数是( )
A. B. C. D.
5.下列关于三角形的外角和的叙述,正确的是( )
A.三角形的外角和等于
B.三角形的外角和就是所有外角的和
C.三角形的内角和等于外角和的一半
D.以上都不对
6.如图, ,且,,则等于( )
A. B. C. D.
7.将一副三角板按照如图方式摆放,则的度数为( )
A. B. C. D.
8.如图,在中,点D,E分别是边AB,BC上的点,连接AE和DE,则下列是的外角的是( )
A. B. C. D.
9.如果将一副三角板按如图方式叠放,那么等于( )
A. B. C. D.
10.已知点D在内,若,,则等于( )
A. B. C. D.
二、填空题
11.如图,已知,,,则 .
12.如图,在中,平分,点在射线上,于,,,则的度数为 .
13.已知直线 ,将含角的直角三角板按如图所示摆放.若,则= .
14.如图,与分别是和的角平分线,则与,之间的数量关系是 .
15.如图,中,,、、、分别是、、、的平分线.
(1) ;
(2) .
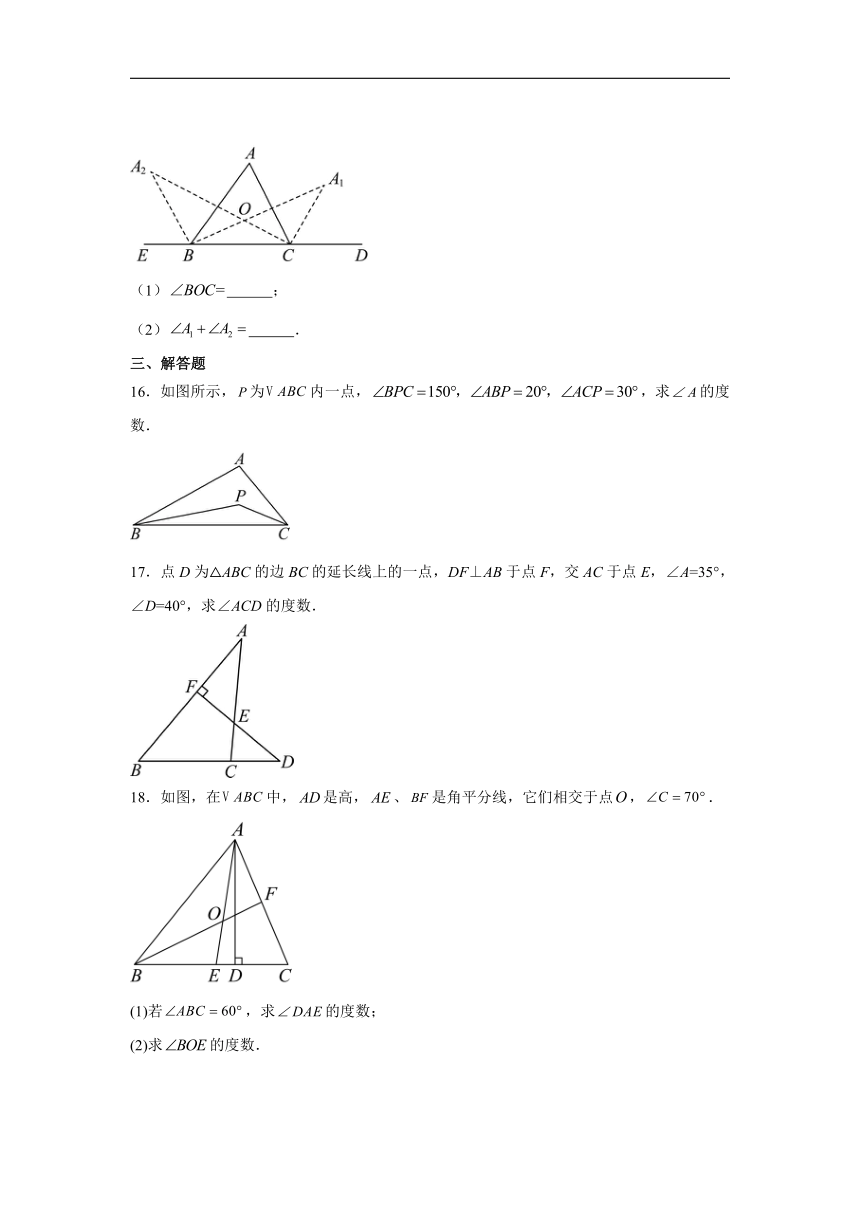
三、解答题
16.如图所示,为内一点,,求的度数.
17.点D为△ABC的边BC的延长线上的一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=40°,求∠ACD的度数.
18.如图,在中,是高,、是角平分线,它们相交于点,.
(1)若,求的度数;
(2)求的度数.
参考答案:
1.C
解:,是的外角,,
,
2.B
解:如图,
∵,
∴,
3.A
∵∠A=32°,∠C=26°,
∴∠DBC=∠A+∠C=58°,
∵DE∥BC,
∴∠D=∠DBC=58°,
4.D
解:如图:
∵,
∴,
∵,
∴,
5.C
解:A、三角形的外角和等于,故本选项不符合题意;
B、三角形的外角和是指每个顶点上取一个外角的和(三个外角的和),故本选项不符合题意;
C、三角形的内角和等于,三角形的外角和等于,所以三角形的内角和等于外角和的一半,故本选项符合题意;
D、本选项不符合题意;
6.D
解:,
,
,
,
.
7.C
解:由题意可得:
,,
∴,
8.C
解:由题意得,∠ADE,∠DEC是△BDE的外角.
9.C
解:如图,
由题意得: ,
由三角形的外角性质得,,
10.C
解:如图:∵、,,
∴,
∵,
∴
,
11.
如图,延长交于点,
由三角形的外角性质可知:,
∵,,
∴,
同理:,
∵,
∴,
故答案为:.
12./34度
解:,,
,
平分,
,
,
,
,
,
,
故答案为:.
13./110度
解:∵角的直角三角板,,
∴,
又∵,根据平行线同位角相等得:,
∵与为对顶角,
∴,
故答案为:.
14.
解:∵与分别是和的角平分线,
∴,,
∵,,
∴,
∴,
∴.
故答案为:.
15.
解:(1)∵,
∴,
∵和分别是和的角平分线,
∴,
∴.
(2)∵、分别是、的角平分线,
∴,,
且,
∴,
即,
同理,
即.
16.
解:延长交于,如图所示:
分别为的外角,
∴,,
∴,
∴.
17.85°
解:∵DF⊥AB于点F,
∴∠DFB=90°
在Rt△DFB中,∠DFB=90°,
∴∠B+∠D=90°
∵∠D=40°,
∴∠B=50°
∵∠ACD是△DFB的外角,∠A=35°,
∴∠ACD=∠B+∠A=50°+35°=85°
18.(1)
(2)
(1)解:是高,,
,
,
,
是的平分线,
,
;
(2)解:,
,
、是角平分线,
,
是的外角,
.
一、单选题
1.如图,,是的外角,,则的大小是( )
A. B. C. D.
2.如果将一副三角板按如图方式叠放,那么等于( )
A. B. C. D.
3.如图,点D在△ABC的边AB的延长线上,DE∥BC,若∠A=32°,∠C=26°,则∠D的度数是( )
A.58° B.59° C.60° D.69°
4.一副三角板如图叠放在一起,则的度数是( )
A. B. C. D.
5.下列关于三角形的外角和的叙述,正确的是( )
A.三角形的外角和等于
B.三角形的外角和就是所有外角的和
C.三角形的内角和等于外角和的一半
D.以上都不对
6.如图, ,且,,则等于( )
A. B. C. D.
7.将一副三角板按照如图方式摆放,则的度数为( )
A. B. C. D.
8.如图,在中,点D,E分别是边AB,BC上的点,连接AE和DE,则下列是的外角的是( )
A. B. C. D.
9.如果将一副三角板按如图方式叠放,那么等于( )
A. B. C. D.
10.已知点D在内,若,,则等于( )
A. B. C. D.
二、填空题
11.如图,已知,,,则 .
12.如图,在中,平分,点在射线上,于,,,则的度数为 .
13.已知直线 ,将含角的直角三角板按如图所示摆放.若,则= .
14.如图,与分别是和的角平分线,则与,之间的数量关系是 .
15.如图,中,,、、、分别是、、、的平分线.
(1) ;
(2) .
三、解答题
16.如图所示,为内一点,,求的度数.
17.点D为△ABC的边BC的延长线上的一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=40°,求∠ACD的度数.
18.如图,在中,是高,、是角平分线,它们相交于点,.
(1)若,求的度数;
(2)求的度数.
参考答案:
1.C
解:,是的外角,,
,
2.B
解:如图,
∵,
∴,
3.A
∵∠A=32°,∠C=26°,
∴∠DBC=∠A+∠C=58°,
∵DE∥BC,
∴∠D=∠DBC=58°,
4.D
解:如图:
∵,
∴,
∵,
∴,
5.C
解:A、三角形的外角和等于,故本选项不符合题意;
B、三角形的外角和是指每个顶点上取一个外角的和(三个外角的和),故本选项不符合题意;
C、三角形的内角和等于,三角形的外角和等于,所以三角形的内角和等于外角和的一半,故本选项符合题意;
D、本选项不符合题意;
6.D
解:,
,
,
,
.
7.C
解:由题意可得:
,,
∴,
8.C
解:由题意得,∠ADE,∠DEC是△BDE的外角.
9.C
解:如图,
由题意得: ,
由三角形的外角性质得,,
10.C
解:如图:∵、,,
∴,
∵,
∴
,
11.
如图,延长交于点,
由三角形的外角性质可知:,
∵,,
∴,
同理:,
∵,
∴,
故答案为:.
12./34度
解:,,
,
平分,
,
,
,
,
,
,
故答案为:.
13./110度
解:∵角的直角三角板,,
∴,
又∵,根据平行线同位角相等得:,
∵与为对顶角,
∴,
故答案为:.
14.
解:∵与分别是和的角平分线,
∴,,
∵,,
∴,
∴,
∴.
故答案为:.
15.
解:(1)∵,
∴,
∵和分别是和的角平分线,
∴,
∴.
(2)∵、分别是、的角平分线,
∴,,
且,
∴,
即,
同理,
即.
16.
解:延长交于,如图所示:
分别为的外角,
∴,,
∴,
∴.
17.85°
解:∵DF⊥AB于点F,
∴∠DFB=90°
在Rt△DFB中,∠DFB=90°,
∴∠B+∠D=90°
∵∠D=40°,
∴∠B=50°
∵∠ACD是△DFB的外角,∠A=35°,
∴∠ACD=∠B+∠A=50°+35°=85°
18.(1)
(2)
(1)解:是高,,
,
,
,
是的平分线,
,
;
(2)解:,
,
、是角平分线,
,
是的外角,
.
