(11)二次函数与一元二次方程—九年级数学人教版上册课前导学(含解析)
文档属性
| 名称 | (11)二次函数与一元二次方程—九年级数学人教版上册课前导学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 454.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 22:56:49 | ||
图片预览

文档简介
(11)二次函数与一元二次方程—九年级数学人教版上册课前导学
一、知识预习
二次函数的图象和x轴交点的横坐标与一元二次方程的根的关系:
抛物线(a≠0) 与x轴的公共点的个数 一元二次方程 (a≠0)的根的情况
>0 有 个 有两个不相等的实数根
=0 有 个 有两个相等的实数根
<0 没有公共点 没有实数根
二、自我检测
1.根据表中二次函数的自变量x与函数值y的对应值,判断一元二次方程的一个根x的取值范围是( )
x 6.17 6.18 6.19 6.20
y -0.03 -0.01 0.02 0.04
A. B.
C. D.
2.铅球运动是利用人体全身的力量,将一定重量的铅球从肩上用手臂推出的田径运动项目之一.如图,将一位运动员所推铅球的行进路线近似地看成一条抛物线,其中铅球行进高度y(m)与水平距离x(m)之间的函数关系式为,则该运动员所推铅球的水平距离为( )
A. B. C. D.
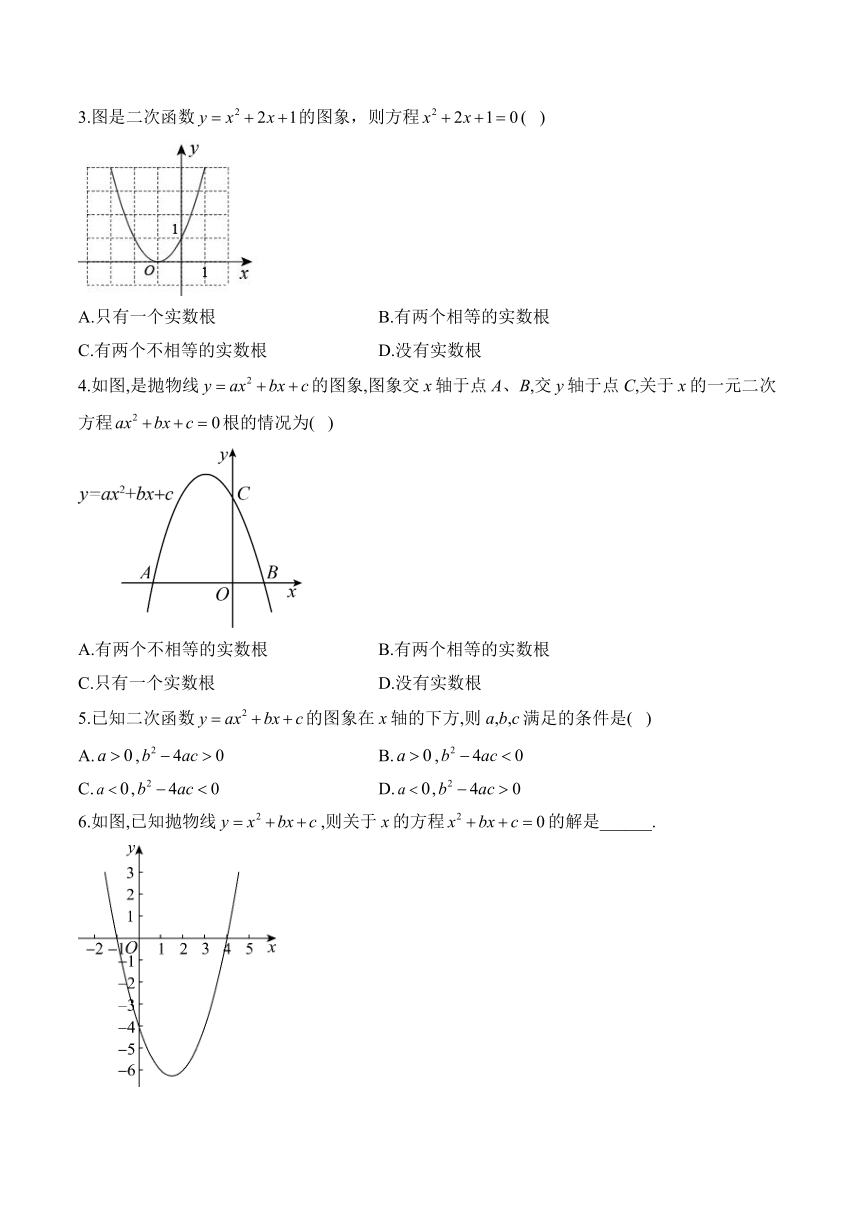
3.图是二次函数的图象,则方程( )
A.只有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
4.如图,是抛物线的图象,图象交x轴于点A、B,交y轴于点C,关于x的一元二次方程根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
5.已知二次函数的图象在x轴的下方,则a,b,c满足的条件是( )
A., B.,
C., D.,
6.如图,已知抛物线,则关于x的方程的解是______.
7.如图,抛物线的顶点坐标是,若关于x的一元二次方程无实数根,则m的取值范围是______.
8.已知的图象如图所示,根据图象回答下列问题.
(1)求方程的解;
(2)如果方程无实数根,求的取值范围.
答案以及解析
一、知识预习
1.两 一
二、自我检测
1.答案:C
解析:当时,,当时,,
一元二次方程的一个根x的取值范围是,
故选:C.
2.答案:A
解析:当时,
解得或,
该运动员所推铅球的水平距离为,
故选:A.
3.答案:B
解析:根据函数图象可得,二次函数与x轴只有一个交点,
方程有两个相等的实数根,故选:B.
4.答案:A
解析:函数图象开口向下.图象交x轴于点A、B,
∴一元二次方程有两个不相等的实数根;故选:A.
5.答案:C
解析:二次函教的图象在x轴的下方,
抛物线开口向下,与x轴无交点,
即,,
故选:C.
6.答案:
解析:由函数图象可知抛物线与x轴交于,,
∴关于x的方程的解是,,
故答案为:,.
7.答案:
解析:∵关于x的一元二次方程无实数根,
∴抛物线与没有交点,
∵抛物线的顶点坐标是,
∴.
故答案为:.
8.答案:(1),;
(2).
解析:(1)观察函数图象可知,图象与轴的交点坐标为,,与轴的交点坐标为,
将方程变形为,
由图象可知方程的解为,,
∴方程的解为,;
(2)若方程无实数根,
则由图象可得,
∴.
一、知识预习
二次函数的图象和x轴交点的横坐标与一元二次方程的根的关系:
抛物线(a≠0) 与x轴的公共点的个数 一元二次方程 (a≠0)的根的情况
>0 有 个 有两个不相等的实数根
=0 有 个 有两个相等的实数根
<0 没有公共点 没有实数根
二、自我检测
1.根据表中二次函数的自变量x与函数值y的对应值,判断一元二次方程的一个根x的取值范围是( )
x 6.17 6.18 6.19 6.20
y -0.03 -0.01 0.02 0.04
A. B.
C. D.
2.铅球运动是利用人体全身的力量,将一定重量的铅球从肩上用手臂推出的田径运动项目之一.如图,将一位运动员所推铅球的行进路线近似地看成一条抛物线,其中铅球行进高度y(m)与水平距离x(m)之间的函数关系式为,则该运动员所推铅球的水平距离为( )
A. B. C. D.
3.图是二次函数的图象,则方程( )
A.只有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
4.如图,是抛物线的图象,图象交x轴于点A、B,交y轴于点C,关于x的一元二次方程根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
5.已知二次函数的图象在x轴的下方,则a,b,c满足的条件是( )
A., B.,
C., D.,
6.如图,已知抛物线,则关于x的方程的解是______.
7.如图,抛物线的顶点坐标是,若关于x的一元二次方程无实数根,则m的取值范围是______.
8.已知的图象如图所示,根据图象回答下列问题.
(1)求方程的解;
(2)如果方程无实数根,求的取值范围.
答案以及解析
一、知识预习
1.两 一
二、自我检测
1.答案:C
解析:当时,,当时,,
一元二次方程的一个根x的取值范围是,
故选:C.
2.答案:A
解析:当时,
解得或,
该运动员所推铅球的水平距离为,
故选:A.
3.答案:B
解析:根据函数图象可得,二次函数与x轴只有一个交点,
方程有两个相等的实数根,故选:B.
4.答案:A
解析:函数图象开口向下.图象交x轴于点A、B,
∴一元二次方程有两个不相等的实数根;故选:A.
5.答案:C
解析:二次函教的图象在x轴的下方,
抛物线开口向下,与x轴无交点,
即,,
故选:C.
6.答案:
解析:由函数图象可知抛物线与x轴交于,,
∴关于x的方程的解是,,
故答案为:,.
7.答案:
解析:∵关于x的一元二次方程无实数根,
∴抛物线与没有交点,
∵抛物线的顶点坐标是,
∴.
故答案为:.
8.答案:(1),;
(2).
解析:(1)观察函数图象可知,图象与轴的交点坐标为,,与轴的交点坐标为,
将方程变形为,
由图象可知方程的解为,,
∴方程的解为,;
(2)若方程无实数根,
则由图象可得,
∴.
同课章节目录
