23.3.3&23.3.4 相似三角形的判定和性质 复习课件(共12张PPT)数学华师大版九年级上册
文档属性
| 名称 | 23.3.3&23.3.4 相似三角形的判定和性质 复习课件(共12张PPT)数学华师大版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 828.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 17:24:26 | ||
图片预览




文档简介
(共12张PPT)
相似三角形的判定和性质
(复习)
如图,在△ABC中,AB>AC,D为AC边上异于A、C的一点,过D点作一直线与AB相交于点E,使所得到的新三角形与原△ABC相似.
问:你能画出符合条件的直线吗?
D
A
C
B
E
E
相似三角形的判定方法
1、平行于三角形一边的直线和
其他两边相交,所构成的三角形
与原三角形相似
2、有两角对应相等的两个三角形相似
苏辙中学
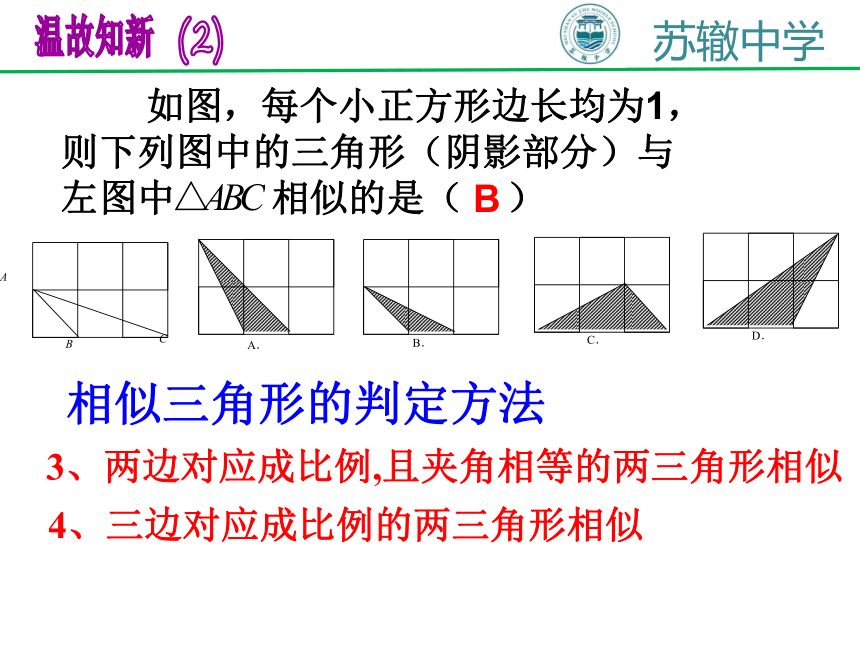
A.
B.
C.
D.
A
B
C
如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中 相似的是( )
3、两边对应成比例,且夹角相等的两三角形相似
4、三边对应成比例的两三角形相似
B
相似三角形的判定方法
苏辙中学
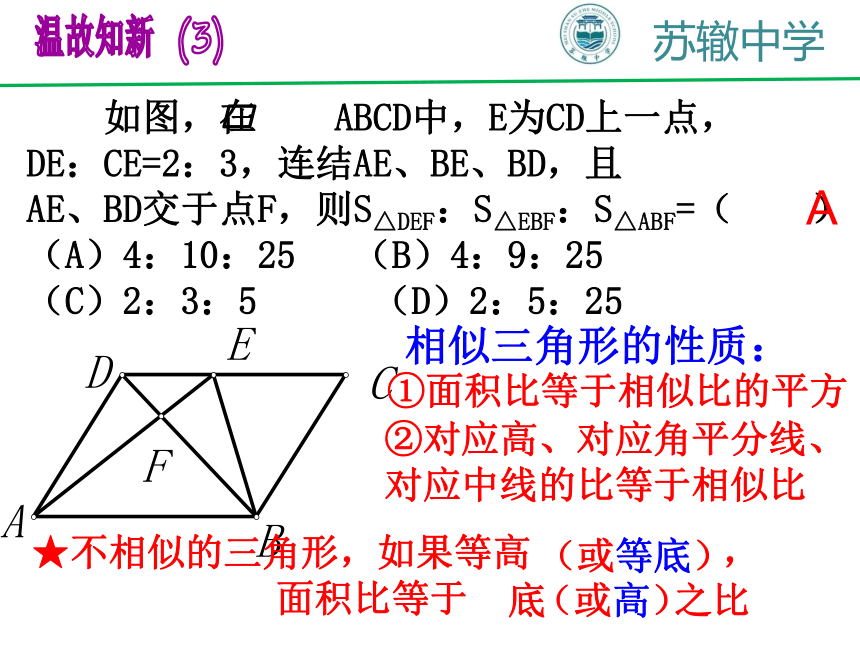
如图,在 ABCD中,E为CD上一点,
DE:CE=2:3,连结AE、BE、BD,且
AE、BD交于点F,则S△DEF:S△EBF:S△ABF=( )
(A)4:10:25 (B)4:9:25
(C)2:3:5 (D)2:5:25
F
E
B
A
C
D
苏辙中学
②对应高、对应角平分线、对应中线的比等于相似比
A
相似三角形的性质:
①面积比等于相似比的平方
★不相似的三角形,如果等高 ,
面积比等于
(或等底)
(或高)
底 之比
例1.如图,△PCD是等边三角形,A、C、D、B在同
一直线上,且∠APB=120°.
求证:⑴△PAC∽△BPD;⑵AC·BD=CD2.
A
B
C
D
P
苏辙中学
例题讲解
求∠APB的度数.
AC·BD=CD2
例2.如图,在平面直角坐标系内,已知点A(0,6),点B(8,0).动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P,Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,△APQ ∽ △AOB
并求出此时点P的坐标.
苏辙中学
例题讲解
△APQ与△AOB相似.
以A,P,Q为顶点的三角形和以点A,O,B为顶点的三角形相似
Q
O
P
Q
A
B
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
(3)当△ADE是等腰三角形时,求AE的长
1
苏辙中学
综合练习
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
(1)求证:△ABD∽△DCE
∵∠ADC是△ABD的外角
∴∠ADC=∠ADE+∠2=∠B+∠1
)2
1
证明:∵AB=AC,∠BAC=90°
∴∠B=∠C=45°
又∵∠ADE=45°
∴∠ADE=∠B
∴∠1=∠2
∴ △ABD∽△DCE
A
B
C
D
E
苏辙中学
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
解:∵△ABD∽△DCE
1
∴
∴
∴
当
时
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
苏辙中学
(3)当△ADE是等腰三角形时,求AE的长
AD=AE
AE=DE
DE=AD
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
1
A
B
C
D
E
分类讨论
苏辙中学
(2018.眉山)如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN. (1)求证:BN平分∠ABE; (3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
苏辙中学
链接中考
A
B
D
E
N
M
C
①
②
A
B
D
E
N
M
C
F
谢 谢
相似三角形的判定和性质
(复习)
如图,在△ABC中,AB>AC,D为AC边上异于A、C的一点,过D点作一直线与AB相交于点E,使所得到的新三角形与原△ABC相似.
问:你能画出符合条件的直线吗?
D
A
C
B
E
E
相似三角形的判定方法
1、平行于三角形一边的直线和
其他两边相交,所构成的三角形
与原三角形相似
2、有两角对应相等的两个三角形相似
苏辙中学
A.
B.
C.
D.
A
B
C
如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中 相似的是( )
3、两边对应成比例,且夹角相等的两三角形相似
4、三边对应成比例的两三角形相似
B
相似三角形的判定方法
苏辙中学
如图,在 ABCD中,E为CD上一点,
DE:CE=2:3,连结AE、BE、BD,且
AE、BD交于点F,则S△DEF:S△EBF:S△ABF=( )
(A)4:10:25 (B)4:9:25
(C)2:3:5 (D)2:5:25
F
E
B
A
C
D
苏辙中学
②对应高、对应角平分线、对应中线的比等于相似比
A
相似三角形的性质:
①面积比等于相似比的平方
★不相似的三角形,如果等高 ,
面积比等于
(或等底)
(或高)
底 之比
例1.如图,△PCD是等边三角形,A、C、D、B在同
一直线上,且∠APB=120°.
求证:⑴△PAC∽△BPD;⑵AC·BD=CD2.
A
B
C
D
P
苏辙中学
例题讲解
求∠APB的度数.
AC·BD=CD2
例2.如图,在平面直角坐标系内,已知点A(0,6),点B(8,0).动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P,Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,△APQ ∽ △AOB
并求出此时点P的坐标.
苏辙中学
例题讲解
△APQ与△AOB相似.
以A,P,Q为顶点的三角形和以点A,O,B为顶点的三角形相似
Q
O
P
Q
A
B
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
(3)当△ADE是等腰三角形时,求AE的长
1
苏辙中学
综合练习
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
(1)求证:△ABD∽△DCE
∵∠ADC是△ABD的外角
∴∠ADC=∠ADE+∠2=∠B+∠1
)2
1
证明:∵AB=AC,∠BAC=90°
∴∠B=∠C=45°
又∵∠ADE=45°
∴∠ADE=∠B
∴∠1=∠2
∴ △ABD∽△DCE
A
B
C
D
E
苏辙中学
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
解:∵△ABD∽△DCE
1
∴
∴
∴
当
时
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
苏辙中学
(3)当△ADE是等腰三角形时,求AE的长
AD=AE
AE=DE
DE=AD
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
1
A
B
C
D
E
分类讨论
苏辙中学
(2018.眉山)如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN. (1)求证:BN平分∠ABE; (3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
苏辙中学
链接中考
A
B
D
E
N
M
C
①
②
A
B
D
E
N
M
C
F
谢 谢
