人教九上培优练:第13课 二次函数与实际问题(含解析)
文档属性
| 名称 | 人教九上培优练:第13课 二次函数与实际问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 21:50:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第13课 二次函数与实际问题
题组A 基础过关练
1.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:
h =﹣5t2+20t﹣14,则小球距离地面的最大高度是( )
A.2米 B.5米 C.6米 D.14米
2.在地球上同一地点,不同质量的物体从同一高度同时下落,如果除地球引力外不考虑其他外力的作用,那么它们的落地时间相同.物体的下落距离h(m)与下落时间t(s)之间的函数表达式为h=gt2.其中g取值为9.8m/s2.小莉进行自由落体实验,她从某建筑物抛下一个小球,经过4s后落地,则该建筑物的高度约为( )
A.98m B.78.4m C.49m D.36.2m
3.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元.若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
4.如图,用绳子围成周长为10m的矩形,记矩形的一边长为xm,矩形的面积为Sm2.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
5.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
6.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
7.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为,那么关于的函数解析式为_________.
8.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB//x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm则右轮廓线DFE所在抛物线的函数表达式为___(不用写x的取值范围).
9.某商场经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价为25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)若商场每天要获得销售利润2000元,销售单价应定为多少元?
(2)求销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
10.如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?
题组B 能力提升练
1.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
2.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
3.飞机着陆后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数表达式为,当滑行时间为10秒时,滑行距离为450米;当滑行时间为20秒时,滑行距离为600米,则飞机的最大滑行距离为( )
A.600米 B.800米 C.1000米 D.1200米
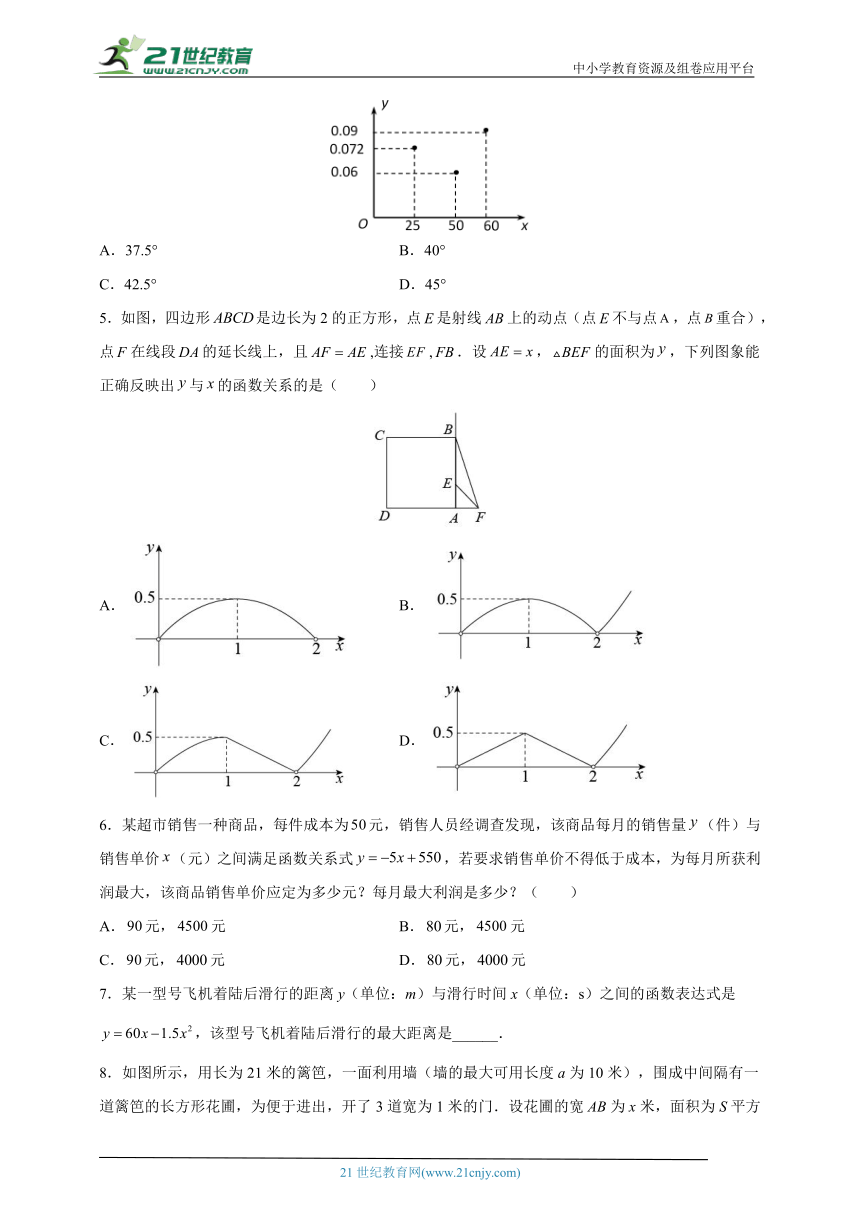
4.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.37.5° B.40°
C.42.5° D.45°
5.如图,四边形是边长为2的正方形,点是射线上的动点(点不与点,点重合),点在线段的延长线上,且,连接,.设,的面积为,下列图象能正确反映出与的函数关系的是( )
A. B.
C. D.
6.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
7.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是,该型号飞机着陆后滑行的最大距离是______.
8.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为__;自变量x的取值范围为 __.
9.为满足市场需求,某超市在中秋节前夕购进价格为12元/盒的某品牌月饼,根据市场预测,该品牌月饼每盒售价14元时,每天能售出200盒,并且售价每上涨1元,其销售量将减少10盒,为了维护消费者利益,物价部门规定:该品牌月饼的售价不能超过20元/盒.
(1)当销售单价为多少元时,该超市每天销售该品牌月饼的利润为720元;
(2)当销售单价为多少元时,超市每天销售该品牌月饼获得利润最大?最大利润是多少?
10.小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
题组C 培优拔尖练
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
2.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
3.如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P,Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t函数关系的图象是( )
A.B.C.D.
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论不正确的是( )
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
A.足球距离地面的最大高度超过20m B.足球飞行路线的对称轴是直线
C.点(10,0)在该抛物线上 D.足球被踢出时,距离地面的高度逐渐下降.
5.2020年6月中旬以来,北京市新冠肺炎疫情出现反弹,北京市民对防疫物资需求量激增.某厂商计划投资产销一种消毒液,设每天产销量为x瓶,每日产销这种消毒液的有关信息如下表:(产销量指生产并销售的数量,生产多少就销售多少,不考虑滞销和脱销)若该消毒液的单日产销利润y元,当销量x为多少时,该消毒液的单日产销利润最大.( )
消毒液 每瓶售价(元) 每瓶成本(元) 每日其他费用(元) 每日最大产销量(瓶)
30 18 1200+0.02x2 250
A.250 B.300 C.200 D.550
6.如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米 B.米 C.米 D.0.4米
7.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
8.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为______.
9.一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
10.某工厂制作A、B两种手工艺品,B每件获利比A多105元,制作16件A与制作2件B获利相同.
(1)制作一件A和一件B分别获利多少元;
(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C工艺品.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等,设每天安排x人制作B,y人制作A.写出y与x之间的函数关系式;
(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作B为5件时,每件B获利不变,若B每增加1件,则当天平均每件B获利减少2元,已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.
题组A 基础过关练
1.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h =﹣5t2+20t﹣14,则小球距离地面的最大高度是( )
A.2米 B.5米 C.6米 D.14米
【答案】C
【详解】高度h和飞行时间t 满足函数关系式:h =﹣5t2+20t﹣14,
当时,小球距离地面高度最大,
米,
故选:C.
2.在地球上同一地点,不同质量的物体从同一高度同时下落,如果除地球引力外不考虑其他外力的作用,那么它们的落地时间相同.物体的下落距离h(m)与下落时间t(s)之间的函数表达式为h=gt2.其中g取值为9.8m/s2.小莉进行自由落体实验,她从某建筑物抛下一个小球,经过4s后落地,则该建筑物的高度约为( )
A.98m B.78.4m C.49m D.36.2m
【答案】B
【详解】解:把t=4代入h=gt2得,
故选:B.
3.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元.若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
【答案】A
【详解】解:设每盆应该多植x株,由题意得
(x+3)(4-0.5x)=15,
故选:A.
4.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
【答案】A
【详解】解:由题意得,
2(x+y)=10,
∴x+y=5,
∴y=5﹣x,
∵S=xy
=x(5﹣x)
∴矩形面积满足的函数关系为S=x(5﹣x),
由题意可知自变量的取值范围为,
故选:A.
5.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
【答案】B
【详解】解:由题意得:,
故选B.
6.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
【答案】C
【详解】解:此炮弹在第6秒与第18秒时的高度相等,
抛物线的对称轴直线是:,
抛物线开口向下,
时,函数值最大,
即第12秒炮弹所在高度最高,
故选:C.
7.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为,那么关于的函数解析式为_________.
【答案】
【详解】解:根据题意可得:2020年的蔬菜产量为,
2021年的蔬菜产量为,
∴,
故答案为: .
8.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB//x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm则右轮廓线DFE所在抛物线的函数表达式为 ___(不用写x的取值范围).
【答案】
【详解】解:∵眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称,AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,
∴点C的坐标为(﹣3,0),点B(﹣1,1),
∴点D(1,1),点F(3,0),
设右轮廓线DFE所在抛物线的函数解析式为:y=a(x﹣3)2,
则1=a(1﹣3)2,
解得,a=,
∴右轮廓线DFE所在抛物线的函数解析式为:
9.某商场经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价为25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)若商场每天要获得销售利润2000元,销售单价应定为多少元?
(2)求销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
【答案】(1)销售单价应定为30元或40元.(2)当单价为35元时,该文具每天的最大利润为2250元.
【详解】解:(1)设销售单价为x元,根据题意列方程得,
(x﹣20)[250﹣10(x﹣25)]=2000,
解得x1=30,x2=40
答:销售单价应定为30元或40元.
(2)设销售单价为x元,每天的销售利润w元,可列函数解析式为:w=(x﹣20)[250﹣10(x﹣25)] =﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250.
∵﹣10<0,
∴函数图象开口向下,当x=35时,w有最大值,最大值为2250元,
答:当单价为35元时,该文具每天的最大利润为2250元.
10.如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG = 2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?
【答案】(1)y=-2x+4x+16;(2)2米
【详解】解:(1)∵BE边长为x米,
∴AE=AB-BE=4-x,AG=AD+DG=4+2x
苗圃的面积=AE×AG=(4-x)(4+2x)
则苗圃的面积y(单位:米2)与x(单位:米)的函数关系式为:y=-2x+4x+16
(2)依题意,令y=16 即-2x+4x+16=16
解得:x=0(舍)x=2
答:此时BE的长为2米.
题组B 能力提升练
1.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
【答案】C
【详解】解:∵AC⊥x轴,OA=5米,
∴点C的横坐标为-5,
当x=-5时,y=-0.01(x-20)2+4=y=-0.01(-5-20)2+4=-2.25,
∴C(-5,-2.25),
∴桥面离水面的高度AC为2.25米.
故选:C.
2.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
【答案】A
【详解】解:∵喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,
设抛物线解析式为,将点代入,得
解得
∴抛物线解析式为
令,解得(负值舍去)
即,
故选:A
3.飞机着陆后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数表达式为,当滑行时间为10秒时,滑行距离为450米;当滑行时间为20秒时,滑行距离为600米,则飞机的最大滑行距离为( )
A.600米 B.800米 C.1000米 D.1200米
【答案】A
【详解】解:∵时,;时,,
∴,解得:,
∴,
∵,
∴当时,S最大,且最大值为600,
即飞机的最大滑行距离为600米,故A正确.
故选:A.
4.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.37.5° B.40°
C.42.5° D.45°
【答案】B
【详解】解:由图象可得,
该函数的对称轴x>且x<50,
∴37.5<x<50,即对称轴位于直线x=37.5与直线x=50之间且靠近直线x=37.5
∴此燃气灶烧开壶水最节省燃气的旋钮角度约为40°,
故选:B.
5.如图,四边形是边长为2的正方形,点是射线上的动点(点不与点,点重合),点在线段的延长线上,且,连接,.设,的面积为,下列图象能正确反映出与的函数关系的是( )
A. B.
C. D.
【答案】B
【详解】解:当点在之间时,即,
,则,
,
图象是开口向下,对称为:的抛物线,
当点在上方时,即,
,则,
,
图象是开口向上的抛物线,
故选:B.
6.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
【答案】B
【详解】解:设每月总利润为,
依题意得:
,此图象开口向下,又,
当时,有最大值,最大值为元.
故选:B.
7.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是,该型号飞机着陆后滑行的最大距离是______.
【答案】600m##600米
【详解】解:∵,
∴x=20时,y取得最大值,最大值=600,
故答案为:600m.
8.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为 __;自变量x的取值范围为 __.
【答案】
【详解】解:设花圃的宽AB为x米,面积为S平方米,
则S与x的之间的函数表达式为:;
由题意可得:,
解得:.
故答案为:,.
9.为满足市场需求,某超市在中秋节前夕购进价格为12元/盒的某品牌月饼,根据市场预测,该品牌月饼每盒售价14元时,每天能售出200盒,并且售价每上涨1元,其销售量将减少10盒,为了维护消费者利益,物价部门规定:该品牌月饼的售价不能超过20元/盒.
(1)当销售单价为多少元时,该超市每天销售该品牌月饼的利润为720元;
(2)当销售单价为多少元时,超市每天销售该品牌月饼获得利润最大?最大利润是多少?
【答案】(1)当销售单价为16元/盒时,该超市每天的利润为720元
(2)当销售单价20元/盒时,超市每天获得利润最大,最大利润是1120元
【详解】(1)解:设销售单价为x元/盒,依据题意得
解得(不符合题意,舍去).
答:当销售单价为16元/盒时,该超市每天的利润为720元.
(2)设销售单价为x元/盒,每天销售该品牌月饼的利润为w元,依据题意得
∵,抛物线开口向下,当时,w随x的增大而增大.
∴时,w最大为1120元
答:当销售单价20元/盒时,超市每天获得利润最大,最大利润是1120元.
10.小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
【答案】(1)
(2)2或6m
【详解】(1)解:根据题意可知抛物线的顶点为,
设抛物线的解析式为,
将点代入,得,
解得,
抛物线的解析式为,
(2)由,令,
得,
解得,
爸爸站在水柱正下方,且距喷水头P水平距离3m,
当她的头顶恰好接触到水柱时,她与爸爸的水平距离为(m),或(m).
题组C 培优拔尖练
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
【答案】D
【详解】∵两个正方形的周长和是10,如果其中一个正方形的边长为,
∴另一个正方形的边长为,
∴这两个正方形的面积的和S关于的函数关系式为,
故选:D.
2.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
【答案】C
【详解】解:设总利润为y元,
∵第档次产品比最低档次产品提高了个档次,
∴每天利润为,
∴当时,产品利润最大,每天获利864元,
故选C.
3.如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P,Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t函数关系的图象是( )
A.B.C.D.
【答案】D
【详解】解:∵正方形边长为4,点P的运动速度为每秒1个单位长度,
∴当点P到达B点时,t=4s,
当t=4s时,点Q运动了4×2=8个单位长度,
此时点Q到达点D,
故点Q的运动轨迹为:点B——点C——点D;
令运动时间为t,
当点Q在BC上运动时,BQ=2t,AP=t
(0当点Q在CD上运动时,AP=t,此时三角形的高=4,
(2≤t<4)
故选:D
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论不正确的是( )
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
A.足球距离地面的最大高度超过20m B.足球飞行路线的对称轴是直线
C.点(10,0)在该抛物线上 D.足球被踢出时,距离地面的高度逐渐下降.
【答案】C
【详解】解:由题意,可得对称轴为,则可得抛物线经过(0,0),(9,0)
设抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
,
∴足球距离地面的最大高度为20.25m>20m,A选项正确,不符合题意;
∴抛物线的对称轴,故B正确,不符合题意;
由二次函数的性质可得,当时,h随t的增大而减小,
∴足球被踢出时,距离地面的高度逐渐下降,D选项正确,不符合题意,
抛物线经过点(9,0),不经过(10,0),
∴点(10,0)不在该抛物线上,C选项错误,符合题意;
故选:C
5.2020年6月中旬以来,北京市新冠肺炎疫情出现反弹,北京市民对防疫物资需求量激增.某厂商计划投资产销一种消毒液,设每天产销量为x瓶,每日产销这种消毒液的有关信息如下表:(产销量指生产并销售的数量,生产多少就销售多少,不考虑滞销和脱销)若该消毒液的单日产销利润y元,当销量x为多少时,该消毒液的单日产销利润最大.( )
消毒液 每瓶售价(元) 每瓶成本(元) 每日其他费用(元) 每日最大产销量(瓶)
30 18 1200+0.02x2 250
A.250 B.300 C.200 D.550
【答案】D
【详解】解:根据题意,得
∴,
∴,
∵,
∴抛物线的开口向下,有最大值,
又∵,
∴当时,,
故选:D
6.如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米 B.米 C.米 D.0.4米
【答案】B
【详解】解:如图,以O为原点,建立平面直角坐标系,
由题意得,对称轴为x=1.25=,A(0,0.8),C(3,0),
设解析式为y=ax2+bx+c,
∴,
解得:,
所以解析式为:y=x2+x+,
当x=2.75时,y=,
∴使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面08﹣=,
故选:B.
7.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
【答案】121
【详解】解:当时,设,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为,
设该食品零售店每天销售这款冷饮产品的利润为w元,
,
∵1<0,
∴当时,w有最大值为121,
故答案为:121.
8.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为______.
【答案】40米
【详解】解:如图,以底部所在的直线为轴,以线段的垂直平分线所在的直线为轴建立平面直角坐标系:
∴,,
设抛物线的解析式为,将代入,得:,
解得:,
∴抛物线的解析式为,
将代入得:,
解得:,
∴,,
∴,
故答案为:40米.
9.一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
【答案】(1)
(2)这一周该商场销售这种商品获得的最大利润为54000元,售价为12元
(3)
【详解】(1)解:设y与x的函数关系式为:
把和代入得,
解得,
∴
(2)解:根据“在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,”
得:
解得,
设利润为w元,根据题意得,
∵
∴当时,w随x的增大而增大,
∵,且x为正整数
∴当时,w取最大值为:
答:这一周该商场销售这种商品获得的最大利润为54000元,售价为12元;
(3)解:根据题意得,-12000m,
∴对称轴为
∵
∴当时,w随x的增大而增大,
∵该商场这种商品售价不大于15元/件时,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.
∴,解得
∵
∴
10.某工厂制作A、B两种手工艺品,B每件获利比A多105元,制作16件A与制作2件B获利相同.
(1)制作一件A和一件B分别获利多少元;
(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C工艺品.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等,设每天安排x人制作B,y人制作A.写出y与x之间的函数关系式;
(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作B为5件时,每件B获利不变,若B每增加1件,则当天平均每件B获利减少2元,已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.
【答案】(1)制作一件A获利15元,制作一件B获利120元;
(2);
(3)最大利润为3198元,此时.
【详解】(1)解:设制作一件获利元,则制作一件获利元,
由题意得:,
解得:,
当时,,
答:制作一件获利15元,制作一件获利120元;
(2)解:设每天安排人制作,人制作A,则人制作,
于是有:,
∴,
答:与之间的函数关系式为;
(3)解:由题意得:,
又∵,
∴,
∵,
∴抛物线的对称轴为直线,
当时,,y的值不是整数,不合题意,
∴不在顶点处取最值,
当时,不是整数,不符合题意;
当时,,
∵a=﹣2<0,
∴当 25<x<65时,y随着x的增大而减小,
∴当x=26时,.
∴此时制作产品的13人,产品的26人,产品的26人,获利最大,最大利润为3198元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第13课 二次函数与实际问题
题组A 基础过关练
1.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:
h =﹣5t2+20t﹣14,则小球距离地面的最大高度是( )
A.2米 B.5米 C.6米 D.14米
2.在地球上同一地点,不同质量的物体从同一高度同时下落,如果除地球引力外不考虑其他外力的作用,那么它们的落地时间相同.物体的下落距离h(m)与下落时间t(s)之间的函数表达式为h=gt2.其中g取值为9.8m/s2.小莉进行自由落体实验,她从某建筑物抛下一个小球,经过4s后落地,则该建筑物的高度约为( )
A.98m B.78.4m C.49m D.36.2m
3.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元.若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
4.如图,用绳子围成周长为10m的矩形,记矩形的一边长为xm,矩形的面积为Sm2.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
5.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
6.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
7.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为,那么关于的函数解析式为_________.
8.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB//x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm则右轮廓线DFE所在抛物线的函数表达式为___(不用写x的取值范围).
9.某商场经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价为25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)若商场每天要获得销售利润2000元,销售单价应定为多少元?
(2)求销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
10.如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?
题组B 能力提升练
1.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
2.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
3.飞机着陆后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数表达式为,当滑行时间为10秒时,滑行距离为450米;当滑行时间为20秒时,滑行距离为600米,则飞机的最大滑行距离为( )
A.600米 B.800米 C.1000米 D.1200米
4.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.37.5° B.40°
C.42.5° D.45°
5.如图,四边形是边长为2的正方形,点是射线上的动点(点不与点,点重合),点在线段的延长线上,且,连接,.设,的面积为,下列图象能正确反映出与的函数关系的是( )
A. B.
C. D.
6.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
7.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是,该型号飞机着陆后滑行的最大距离是______.
8.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为__;自变量x的取值范围为 __.
9.为满足市场需求,某超市在中秋节前夕购进价格为12元/盒的某品牌月饼,根据市场预测,该品牌月饼每盒售价14元时,每天能售出200盒,并且售价每上涨1元,其销售量将减少10盒,为了维护消费者利益,物价部门规定:该品牌月饼的售价不能超过20元/盒.
(1)当销售单价为多少元时,该超市每天销售该品牌月饼的利润为720元;
(2)当销售单价为多少元时,超市每天销售该品牌月饼获得利润最大?最大利润是多少?
10.小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
题组C 培优拔尖练
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
2.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
3.如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P,Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t函数关系的图象是( )
A.B.C.D.
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论不正确的是( )
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
A.足球距离地面的最大高度超过20m B.足球飞行路线的对称轴是直线
C.点(10,0)在该抛物线上 D.足球被踢出时,距离地面的高度逐渐下降.
5.2020年6月中旬以来,北京市新冠肺炎疫情出现反弹,北京市民对防疫物资需求量激增.某厂商计划投资产销一种消毒液,设每天产销量为x瓶,每日产销这种消毒液的有关信息如下表:(产销量指生产并销售的数量,生产多少就销售多少,不考虑滞销和脱销)若该消毒液的单日产销利润y元,当销量x为多少时,该消毒液的单日产销利润最大.( )
消毒液 每瓶售价(元) 每瓶成本(元) 每日其他费用(元) 每日最大产销量(瓶)
30 18 1200+0.02x2 250
A.250 B.300 C.200 D.550
6.如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米 B.米 C.米 D.0.4米
7.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
8.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为______.
9.一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
10.某工厂制作A、B两种手工艺品,B每件获利比A多105元,制作16件A与制作2件B获利相同.
(1)制作一件A和一件B分别获利多少元;
(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C工艺品.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等,设每天安排x人制作B,y人制作A.写出y与x之间的函数关系式;
(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作B为5件时,每件B获利不变,若B每增加1件,则当天平均每件B获利减少2元,已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.
题组A 基础过关练
1.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h =﹣5t2+20t﹣14,则小球距离地面的最大高度是( )
A.2米 B.5米 C.6米 D.14米
【答案】C
【详解】高度h和飞行时间t 满足函数关系式:h =﹣5t2+20t﹣14,
当时,小球距离地面高度最大,
米,
故选:C.
2.在地球上同一地点,不同质量的物体从同一高度同时下落,如果除地球引力外不考虑其他外力的作用,那么它们的落地时间相同.物体的下落距离h(m)与下落时间t(s)之间的函数表达式为h=gt2.其中g取值为9.8m/s2.小莉进行自由落体实验,她从某建筑物抛下一个小球,经过4s后落地,则该建筑物的高度约为( )
A.98m B.78.4m C.49m D.36.2m
【答案】B
【详解】解:把t=4代入h=gt2得,
故选:B.
3.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元.若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
【答案】A
【详解】解:设每盆应该多植x株,由题意得
(x+3)(4-0.5x)=15,
故选:A.
4.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A. B.
C. D.
【答案】A
【详解】解:由题意得,
2(x+y)=10,
∴x+y=5,
∴y=5﹣x,
∵S=xy
=x(5﹣x)
∴矩形面积满足的函数关系为S=x(5﹣x),
由题意可知自变量的取值范围为,
故选:A.
5.某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
【答案】B
【详解】解:由题意得:,
故选B.
6.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
【答案】C
【详解】解:此炮弹在第6秒与第18秒时的高度相等,
抛物线的对称轴直线是:,
抛物线开口向下,
时,函数值最大,
即第12秒炮弹所在高度最高,
故选:C.
7.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为,那么关于的函数解析式为_________.
【答案】
【详解】解:根据题意可得:2020年的蔬菜产量为,
2021年的蔬菜产量为,
∴,
故答案为: .
8.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB//x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm则右轮廓线DFE所在抛物线的函数表达式为 ___(不用写x的取值范围).
【答案】
【详解】解:∵眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称,AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,
∴点C的坐标为(﹣3,0),点B(﹣1,1),
∴点D(1,1),点F(3,0),
设右轮廓线DFE所在抛物线的函数解析式为:y=a(x﹣3)2,
则1=a(1﹣3)2,
解得,a=,
∴右轮廓线DFE所在抛物线的函数解析式为:
9.某商场经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价为25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)若商场每天要获得销售利润2000元,销售单价应定为多少元?
(2)求销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
【答案】(1)销售单价应定为30元或40元.(2)当单价为35元时,该文具每天的最大利润为2250元.
【详解】解:(1)设销售单价为x元,根据题意列方程得,
(x﹣20)[250﹣10(x﹣25)]=2000,
解得x1=30,x2=40
答:销售单价应定为30元或40元.
(2)设销售单价为x元,每天的销售利润w元,可列函数解析式为:w=(x﹣20)[250﹣10(x﹣25)] =﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250.
∵﹣10<0,
∴函数图象开口向下,当x=35时,w有最大值,最大值为2250元,
答:当单价为35元时,该文具每天的最大利润为2250元.
10.如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG = 2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?
【答案】(1)y=-2x+4x+16;(2)2米
【详解】解:(1)∵BE边长为x米,
∴AE=AB-BE=4-x,AG=AD+DG=4+2x
苗圃的面积=AE×AG=(4-x)(4+2x)
则苗圃的面积y(单位:米2)与x(单位:米)的函数关系式为:y=-2x+4x+16
(2)依题意,令y=16 即-2x+4x+16=16
解得:x=0(舍)x=2
答:此时BE的长为2米.
题组B 能力提升练
1.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
【答案】C
【详解】解:∵AC⊥x轴,OA=5米,
∴点C的横坐标为-5,
当x=-5时,y=-0.01(x-20)2+4=y=-0.01(-5-20)2+4=-2.25,
∴C(-5,-2.25),
∴桥面离水面的高度AC为2.25米.
故选:C.
2.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
【答案】A
【详解】解:∵喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,
设抛物线解析式为,将点代入,得
解得
∴抛物线解析式为
令,解得(负值舍去)
即,
故选:A
3.飞机着陆后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数表达式为,当滑行时间为10秒时,滑行距离为450米;当滑行时间为20秒时,滑行距离为600米,则飞机的最大滑行距离为( )
A.600米 B.800米 C.1000米 D.1200米
【答案】A
【详解】解:∵时,;时,,
∴,解得:,
∴,
∵,
∴当时,S最大,且最大值为600,
即飞机的最大滑行距离为600米,故A正确.
故选:A.
4.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.37.5° B.40°
C.42.5° D.45°
【答案】B
【详解】解:由图象可得,
该函数的对称轴x>且x<50,
∴37.5<x<50,即对称轴位于直线x=37.5与直线x=50之间且靠近直线x=37.5
∴此燃气灶烧开壶水最节省燃气的旋钮角度约为40°,
故选:B.
5.如图,四边形是边长为2的正方形,点是射线上的动点(点不与点,点重合),点在线段的延长线上,且,连接,.设,的面积为,下列图象能正确反映出与的函数关系的是( )
A. B.
C. D.
【答案】B
【详解】解:当点在之间时,即,
,则,
,
图象是开口向下,对称为:的抛物线,
当点在上方时,即,
,则,
,
图象是开口向上的抛物线,
故选:B.
6.某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
【答案】B
【详解】解:设每月总利润为,
依题意得:
,此图象开口向下,又,
当时,有最大值,最大值为元.
故选:B.
7.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是,该型号飞机着陆后滑行的最大距离是______.
【答案】600m##600米
【详解】解:∵,
∴x=20时,y取得最大值,最大值=600,
故答案为:600m.
8.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为 __;自变量x的取值范围为 __.
【答案】
【详解】解:设花圃的宽AB为x米,面积为S平方米,
则S与x的之间的函数表达式为:;
由题意可得:,
解得:.
故答案为:,.
9.为满足市场需求,某超市在中秋节前夕购进价格为12元/盒的某品牌月饼,根据市场预测,该品牌月饼每盒售价14元时,每天能售出200盒,并且售价每上涨1元,其销售量将减少10盒,为了维护消费者利益,物价部门规定:该品牌月饼的售价不能超过20元/盒.
(1)当销售单价为多少元时,该超市每天销售该品牌月饼的利润为720元;
(2)当销售单价为多少元时,超市每天销售该品牌月饼获得利润最大?最大利润是多少?
【答案】(1)当销售单价为16元/盒时,该超市每天的利润为720元
(2)当销售单价20元/盒时,超市每天获得利润最大,最大利润是1120元
【详解】(1)解:设销售单价为x元/盒,依据题意得
解得(不符合题意,舍去).
答:当销售单价为16元/盒时,该超市每天的利润为720元.
(2)设销售单价为x元/盒,每天销售该品牌月饼的利润为w元,依据题意得
∵,抛物线开口向下,当时,w随x的增大而增大.
∴时,w最大为1120元
答:当销售单价20元/盒时,超市每天获得利润最大,最大利润是1120元.
10.小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
【答案】(1)
(2)2或6m
【详解】(1)解:根据题意可知抛物线的顶点为,
设抛物线的解析式为,
将点代入,得,
解得,
抛物线的解析式为,
(2)由,令,
得,
解得,
爸爸站在水柱正下方,且距喷水头P水平距离3m,
当她的头顶恰好接触到水柱时,她与爸爸的水平距离为(m),或(m).
题组C 培优拔尖练
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
【答案】D
【详解】∵两个正方形的周长和是10,如果其中一个正方形的边长为,
∴另一个正方形的边长为,
∴这两个正方形的面积的和S关于的函数关系式为,
故选:D.
2.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
【答案】C
【详解】解:设总利润为y元,
∵第档次产品比最低档次产品提高了个档次,
∴每天利润为,
∴当时,产品利润最大,每天获利864元,
故选C.
3.如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P,Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t函数关系的图象是( )
A.B.C.D.
【答案】D
【详解】解:∵正方形边长为4,点P的运动速度为每秒1个单位长度,
∴当点P到达B点时,t=4s,
当t=4s时,点Q运动了4×2=8个单位长度,
此时点Q到达点D,
故点Q的运动轨迹为:点B——点C——点D;
令运动时间为t,
当点Q在BC上运动时,BQ=2t,AP=t
(0
(2≤t<4)
故选:D
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论不正确的是( )
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
A.足球距离地面的最大高度超过20m B.足球飞行路线的对称轴是直线
C.点(10,0)在该抛物线上 D.足球被踢出时,距离地面的高度逐渐下降.
【答案】C
【详解】解:由题意,可得对称轴为,则可得抛物线经过(0,0),(9,0)
设抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
,
∴足球距离地面的最大高度为20.25m>20m,A选项正确,不符合题意;
∴抛物线的对称轴,故B正确,不符合题意;
由二次函数的性质可得,当时,h随t的增大而减小,
∴足球被踢出时,距离地面的高度逐渐下降,D选项正确,不符合题意,
抛物线经过点(9,0),不经过(10,0),
∴点(10,0)不在该抛物线上,C选项错误,符合题意;
故选:C
5.2020年6月中旬以来,北京市新冠肺炎疫情出现反弹,北京市民对防疫物资需求量激增.某厂商计划投资产销一种消毒液,设每天产销量为x瓶,每日产销这种消毒液的有关信息如下表:(产销量指生产并销售的数量,生产多少就销售多少,不考虑滞销和脱销)若该消毒液的单日产销利润y元,当销量x为多少时,该消毒液的单日产销利润最大.( )
消毒液 每瓶售价(元) 每瓶成本(元) 每日其他费用(元) 每日最大产销量(瓶)
30 18 1200+0.02x2 250
A.250 B.300 C.200 D.550
【答案】D
【详解】解:根据题意,得
∴,
∴,
∵,
∴抛物线的开口向下,有最大值,
又∵,
∴当时,,
故选:D
6.如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米 B.米 C.米 D.0.4米
【答案】B
【详解】解:如图,以O为原点,建立平面直角坐标系,
由题意得,对称轴为x=1.25=,A(0,0.8),C(3,0),
设解析式为y=ax2+bx+c,
∴,
解得:,
所以解析式为:y=x2+x+,
当x=2.75时,y=,
∴使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面08﹣=,
故选:B.
7.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
【答案】121
【详解】解:当时,设,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为,
设该食品零售店每天销售这款冷饮产品的利润为w元,
,
∵1<0,
∴当时,w有最大值为121,
故答案为:121.
8.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为______.
【答案】40米
【详解】解:如图,以底部所在的直线为轴,以线段的垂直平分线所在的直线为轴建立平面直角坐标系:
∴,,
设抛物线的解析式为,将代入,得:,
解得:,
∴抛物线的解析式为,
将代入得:,
解得:,
∴,,
∴,
故答案为:40米.
9.一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
【答案】(1)
(2)这一周该商场销售这种商品获得的最大利润为54000元,售价为12元
(3)
【详解】(1)解:设y与x的函数关系式为:
把和代入得,
解得,
∴
(2)解:根据“在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,”
得:
解得,
设利润为w元,根据题意得,
∵
∴当时,w随x的增大而增大,
∵,且x为正整数
∴当时,w取最大值为:
答:这一周该商场销售这种商品获得的最大利润为54000元,售价为12元;
(3)解:根据题意得,-12000m,
∴对称轴为
∵
∴当时,w随x的增大而增大,
∵该商场这种商品售价不大于15元/件时,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.
∴,解得
∵
∴
10.某工厂制作A、B两种手工艺品,B每件获利比A多105元,制作16件A与制作2件B获利相同.
(1)制作一件A和一件B分别获利多少元;
(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C工艺品.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等,设每天安排x人制作B,y人制作A.写出y与x之间的函数关系式;
(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作B为5件时,每件B获利不变,若B每增加1件,则当天平均每件B获利减少2元,已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.
【答案】(1)制作一件A获利15元,制作一件B获利120元;
(2);
(3)最大利润为3198元,此时.
【详解】(1)解:设制作一件获利元,则制作一件获利元,
由题意得:,
解得:,
当时,,
答:制作一件获利15元,制作一件获利120元;
(2)解:设每天安排人制作,人制作A,则人制作,
于是有:,
∴,
答:与之间的函数关系式为;
(3)解:由题意得:,
又∵,
∴,
∵,
∴抛物线的对称轴为直线,
当时,,y的值不是整数,不合题意,
∴不在顶点处取最值,
当时,不是整数,不符合题意;
当时,,
∵a=﹣2<0,
∴当 25<x<65时,y随着x的增大而减小,
∴当x=26时,.
∴此时制作产品的13人,产品的26人,产品的26人,获利最大,最大利润为3198元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
