人教九上培优练:第10课 二次函数y=ax2+bx+c(a≠0)的图象与性质(含解析)
文档属性
| 名称 | 人教九上培优练:第10课 二次函数y=ax2+bx+c(a≠0)的图象与性质(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第10课 二次函数y=ax2+bx+c(a≠0)的图象与性质
题组A 基础过关练
1.抛物线经过点(m,3),则代数式的值为( )
A.0 B.1 C.2 D.3
2.二次函数(a≠0)中x,y的部分对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 ﹣4 ﹣6 ﹣6 ﹣4 …
则该二次函数图象的对称轴为( )
A.y轴 B.直线x= C.直线x=1 D.直线x=
3.若二次函数y=x2+2x+k的图象经过点(1,y1),(﹣2,y2),则y1,y2与的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
4.已知(﹣4,y1),(2.5,y2),(5,y3)是抛物线y=﹣3x2﹣6x+m上的点,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y1>y3
5.已知函数y=a﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.若a>0,则当x≥1时,y随x的增大而减小 B.若a<0,则当x≤1时,y随x的增大而增大
C.当a=1时,函数图像过点(﹣1,1) D.当a=﹣2时,函数图像与x轴没有交点
6.已知二次函数的图象如图所示,有以下4个结论:①;②;③;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.已知二次函数y=x2-4x-m的最小值是1,则m=_______.
8.二次函数的图象过点,,若当时.随着的增大而减小,则实数的取值范围是______.
9.已知抛物线y=ax2-2ax-3+2a2 (a<0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求抛物线的函数解析式;
10.已知抛物线.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当为何值时,函数取得最大值,请求出这个最大值.
题组B 能力提升练
1.将二次函数的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为,则、的值为( )
A., B.,
C., D.,
2.如图是二次函数y=ax2﹣x+a2﹣9图象,图象过坐标原点,则a的值是( )
A.a=3 B.a=-3 C.a=-9 D.a=3或a=﹣3
3.已知二次函数,当函数值y随x值的增大而增大时,x的取值范围是( )
A. B. C. D.
4.已知抛物线的最低点的纵坐标为,则抛物线的表达式是( )
A. B. C. D.
5.直线与抛物线在同一平面直角坐标系中的图像可能是( )
A. B. C. D.
6.二次函数()的部分图象如图所示,图象过点(,0),对称轴为直线,下列结论:(1);(2); (3);(4)若点A(,),点B(,),点C(,)在该函数图象上,则;(5)m为任意实数,则.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
7.已知二次函数,当时,自变量的取值范围是______.
8.如图,抛物线的对称轴为直线,点A,B均在抛物线上,且与x轴平行,其中点A的坐标为,则点B的坐标为_____.
9.如图,在平面直角坐标系中,抛物线经过点A(﹣1,0),B(4,0),C(0,﹣2).
(1)求此抛物线的解析式和对称轴.
(2)在此抛物线的对称轴上是否存在点P,使△PAC的周长最小?若存在,请求出点P的坐标;若不存在,说明理由.
10.如图,已知抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,直接写出y的取值范围;
题组C 培优拔尖练
1.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
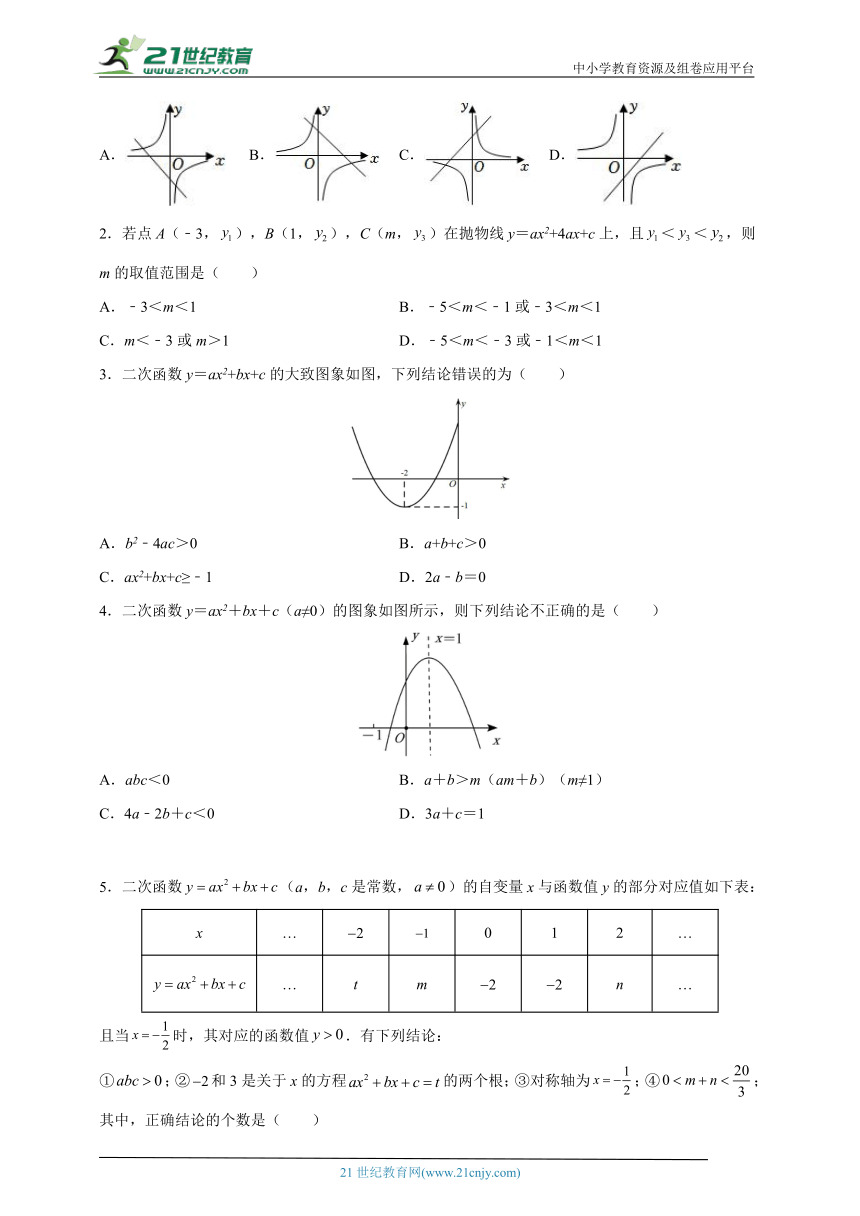
2.若点A(﹣3,),B(1,),C(m,)在抛物线y=ax2+4ax+c上,且<<,则m的取值范围是( )
A.﹣3<m<1 B.﹣5<m<﹣1或﹣3<m<1
C.m<﹣3或m>1 D.﹣5<m<﹣3或﹣1<m<1
3.二次函数y=ax2+bx+c的大致图象如图,下列结论错误的为( )
A.b2﹣4ac>0 B.a+b+c>0
C.ax2+bx+c≥﹣1 D.2a﹣b=0
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
A.abc<0 B.a+b>m(am+b)(m≠1)
C.4a﹣2b+c<0 D.3a+c=1
5.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x … 0 1 2 …
… t m n …
且当时,其对应的函数值.有下列结论:
①;②和3是关于x的方程的两个根;③对称轴为;④;其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6.已知抛物线(c为常数)经过点,,,当时,则m的取值范围为( )
A. B.
C. D.
7.已知二次函数,当时,函数的最大值为8,则的值是____.
8.若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是____________.
9.已知抛物线的顶点(0,1).
(1)求该抛物线的解析式;
(2)如图1,直线交x轴于A,交抛物线于B、C,BE⊥x轴于E,CF⊥x轴于F,试比较AE AF与4的大小关系.
(3)如图2,D(0,2),M(1,3),抛物线上是否存在点N,使得取得最小值,若存在,求出N的坐标,若不存在,说明理由.
10.北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为,着陆坡顶端与落地点的距离为米,若斜坡的坡度(即.求:
(1)点的坐标;
(2)该抛物线的函数表达式;
(3)起跳点与着陆坡顶端之间的水平距离的长.(精确到米)(参考数据:)
题组A 基础过关练
1.抛物线经过点(m,3),则代数式的值为( )
A.0 B.1 C.2 D.3
【答案】D
【详解】解:将点(m,3)代入中得,
,
故代数式的值为3,
故选:D.
2.二次函数(a≠0)中x,y的部分对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 ﹣4 ﹣6 ﹣6 ﹣4 …
则该二次函数图象的对称轴为( )
A.y轴 B.直线x= C.直线x=1 D.直线x=
【答案】B
【详解】解:由图表可知:
x=0时,y=-6,
x=1时,y=-6,
∴二次函数的对称轴为:,
故选:B.
3.若二次函数y=x2+2x+k的图象经过点(1,y1),(﹣2,y2),则y1,y2与的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
【答案】A
【详解】解:当x=1时,y1=x2+2x+k=1+2+k=k+3;
当x=﹣2时,y2=x2+2x+k=4﹣4+k=k,
所以y1>y2.
故选:A.
4.已知(﹣4,y1),(2.5,y2),(5,y3)是抛物线y=﹣3x2﹣6x+m上的点,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y1>y3
【答案】A
【详解】解:∵y=﹣3x2﹣6x+m,
∴抛物线开口向下,对称轴为直线x=﹣=﹣1,
∴与直线x=﹣1距离越近的点的纵坐标越大,
∵﹣1﹣(﹣4)<2.5﹣(﹣1)<5﹣(﹣1),
∴y1>y2>y3,
故选:A.
5.已知函数y=a﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.若a>0,则当x≥1时,y随x的增大而减小 B.若a<0,则当x≤1时,y随x的增大而增大
C.当a=1时,函数图像过点(﹣1,1) D.当a=﹣2时,函数图像与x轴没有交点
【答案】B
【详解】解:A、抛物线的对称轴为直线:,则若a>0,则当x≥1时,y随x的增大而增大,选项说法错误,不符合题意;
B、抛物线的对称轴为直线:,若a<0,则当x≤1时,y随x的增大而增大,选项说法正确,符合题意;
C、当,时,,则当a=1时,函数图像不经过点(﹣1,1),选项说法错误,不符合题意;
D、当a=﹣2时,,,则函数图像与x轴有两个交点,选项说法错误,不符合题意;
故选B.
6.已知二次函数的图象如图所示,有以下4个结论:①;②;③;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【详解】解:①抛物线开口向下,
,
∵,
∴,
,
抛物线与轴的交点在轴的正半轴,
,
,故错误;
②观察函数图象,可知:
当时,,
,故错误.
③抛物线的对称轴为,抛物线与轴的交点在轴的正半轴,
当时,,
,故正确;
④抛物线与轴有2个交点,
△,故正确.
故选:B.
7.已知二次函数y=x2-4x-m的最小值是1,则m=_______.
【答案】-5
【详解】解:由知,
当x=2时,y有最小值为-4-m,
∵该函数的最小值为1,
∴-4-m=1,
解得:m=-5,
故答案为:-5.
8.二次函数的图象过点,,若当时.随着的增大而减小,则实数的取值范围是______.
【答案】且
【详解】解:将代入得①,
将代入得②,
由②①得,
,,
抛物线的对称轴为直线,
当时.随着的增大而减小,
时,,
解得,
时,,
解得,
故答案为:且.
9.已知抛物线y=ax2-2ax-3+2a2 (a<0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求抛物线的函数解析式;
【答案】(1)x=1
(2)y=-x2+2x-1
【详解】(1)解:∵抛物线,
∴抛物线的对称轴为直线x=1;
(2)由(1)可得,
∵抛物线的顶点在x轴上,
∴,
解得,=-1,
∵a<0,
∴a=-1,
∴抛物线的解析式为.
10.已知抛物线.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当为何值时,函数取得最大值,请求出这个最大值.
【答案】(1)抛物线开口向下,对称轴是直线,顶点坐标是
(2)当时,函数取得最大值,最大值是3.
【详解】(1)解:∵-1<0,
∴抛物线开口向下,
对称轴是直线,
∵,
∴顶点坐标是;
(2)∵抛物线的顶点坐标是,
∴当时,函数取得最大值,最大值是3.
题组B 能力提升练
1.将二次函数的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为,则、的值为( )
A., B.,
C., D.,
【答案】D
【详解】由题意可得新抛物线的顶点为,
∴原抛物线的顶点为,
设原抛物线的解析式为,
代入得:,
∴,.
故选:D.
2.如图是二次函数y=ax2﹣x+a2﹣9图象,图象过坐标原点,则a的值是( )
A.a=3 B.a=-3 C.a=-9 D.a=3或a=﹣3
【答案】A
【详解】解:∵抛物线经过原点,
∴a2-9=0, 解得a=3或a=-3,
∵抛物线开口向上,
∴a=3,
故选:A.
3.已知二次函数,当函数值y随x值的增大而增大时,x的取值范围是( )
A. B. C. D.
【答案】B
【详解】解:∵
∵开口向上,对称轴为x=1,
∴x>1时,函数值y随x的增大而增大.
故选:B.
4.已知抛物线的最低点的纵坐标为,则抛物线的表达式是( )
A. B. C. D.
【答案】B
【详解】解:∵抛物线的最低点的纵坐标为,
∴,
即
∴,
当m=1时,抛物线为.
故选:B.
5.直线与抛物线在同一平面直角坐标系中的图像可能是( )
A. B. C. D.
【答案】B
【详解】解:A、由抛物线可知,a>0,b<0,c>0,则ac>0,由直线可知,ac>0,b>0,故本选项不合题意;
B、由抛物线可知,a>0,b>0,c>0,则ac>0,由直线可知,ac>0,b>0,故本选项符合题意;
C、由抛物线可知,a<0,b<0,c>0,则ac<0,由直线可知,ac>0,b>0,故本选项不合题意;
D、由抛物线可知,a<0,b>0,c>0,则ac<0,由直线可知,ac<0,b<0,故本选项不合题意.
故选:B.
6.二次函数()的部分图象如图所示,图象过点(,0),对称轴为直线,下列结论:(1); (2); (3);(4)若点A(,),点B(,),点C(,)在该函数图象上,则;(5)m为任意实数,则.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
【答案】A
【详解】解:∵对称轴为直线x=2,
∴-=2,
∴b=-4a,
∴b+4a=0,
∴(1)正确;
∵经过点(-1,0),
∴a-b+c=0,
∴c=b-a=-4a-a=-5a,
∴4a+c-2b=4a-5a+8a=7a,
∵a<0,
∴4a+c-2b<0,
∴4a+c<2b,
∴(2)不正确;
∵5a+3c=5a-15a=-10a>0,
∴(3)正确;
∵|-2-2|=4,|-2|=,|-2|=,
∴y1<y2<y3,
∴(4)不正确;
当x=2时,函数有最大值4a+2b+c,
∴am2+bm+c≤4a+2b+c,
∴(5)不正确;
综上所述:(1)(3)正确,
故选:A.
7.已知二次函数,当时,自变量的取值范围是______.
【答案】x≤-2或x≥4
【详解】解:∵二次函数,
∴抛物线开口向上,对称轴为直线,
∴当时,y随x的增大而减小,当时,y随x的增大而增大,
当时,则,
即,
解得,或,
∴当时,自变量x的取值范围是或,
故答案为:或.
8.如图,抛物线的对称轴为直线,点A,B均在抛物线上,且与x轴平行,其中点A的坐标为,则点B的坐标为_____.
【答案】(6,5)
【详解】∵AB与x轴平行,
而点A,B均在抛物线上,
∴点A与点B关于直线x=1对称,
∵点A的坐标为,
∴B点坐标为,
故答案为.
9.如图,在平面直角坐标系中,抛物线经过点A(﹣1,0),B(4,0),C(0,﹣2).
(1)求此抛物线的解析式和对称轴.
(2)在此抛物线的对称轴上是否存在点P,使△PAC的周长最小?若存在,请求出点P的坐标;若不存在,说明理由.
【答案】(1)y=x2﹣x﹣2;对称轴为x=
(2)存在,P的坐标为(,﹣)
【详解】(1)解:设该抛物线的解析式为y=ax2+bx+c,
∵该抛物线过点A(﹣1,0),B(4,0),C(0,﹣2),代入,得:
解得:
∴此抛物线的解析式为y=x2﹣x﹣2.
∵抛物线解析式为y=x2﹣x﹣2=﹣
∴抛物线的对称轴为x= .
(2)解:存在,理由如下:
连接PB
由抛物线的对称性得:PA=PB
∴△PAC的周长PA+PC+AC=PB+PC+AC,
∴当B、P、C三点共线时,PB+PC最小,
即当B、P、C三点共线时,△PAC的周长最小,
设直线BC的解析式为y=kx+m,
将点B(4,0),点C(0,﹣2)代入,
得,解得:,
即直线BC的解析式为y=x﹣2.
令x=,则有y=﹣2=﹣,
即点P的坐标为(,﹣).
∴在此抛物线的对称轴上存在点P,使△PAC的周长最小,此时点P的坐标为(,﹣).
10.如图,已知抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,直接写出y的取值范围;
【答案】(1),顶点坐标为(1,4);
(2)0<y≤4
【详解】(1)解:将A( 1,0)和B(3,0)代入y= x2+bx+c,得,解得:,∴抛物线的解析式为:,∵,∴抛物线的顶点坐标为(1,4);
(2)∵当x=1时,y=4;当x=3时,y=0,∴由函数图象可得:当0<x<3时,0<y≤4.
题组C 培优拔尖练
1.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
【答案】D
【详解】解:∵二次函数图象开口方向向下,
∴a<0,
∵对称轴为直线>0,
∴b>0,
∵与y轴的负半轴相交,
∴c<0,
∴y=bx+c的图象经过第一、三、四象限,
反比例函数y=图象在第二四象限,
只有D选项图象符合.
故选:D.
2.若点A(﹣3,),B(1,),C(m,)在抛物线y=ax2+4ax+c上,且<<,则m的取值范围是( )
A.﹣3<m<1 B.﹣5<m<﹣1或﹣3<m<1
C.m<﹣3或m>1 D.﹣5<m<﹣3或﹣1<m<1
【答案】D
【详解】解:抛物线y=ax2+4ax+c的对称轴为x=﹣=﹣2,
∵点A(﹣3,y1),B(1,y2),C(m,y3)在抛物线y=ax2+4ax+c上,且y1<y3<y2,
∴当a<0,则|m+2|<1且|m+2|>3,(不存在);
当a>0,则1<|m+2|<3,解得﹣5<m<﹣3或﹣1<m<1.
故选:D.
3.二次函数y=ax2+bx+c的大致图象如图,下列结论错误的为( )
A.b2﹣4ac>0 B.a+b+c>0
C.ax2+bx+c≥﹣1 D.2a﹣b=0
【答案】D
【详解】解:由图象可知,抛物线与x轴有两个交点,所以b2﹣4ac>0,故选项A正确不符合题意;
由图象可知,当x=1时,y>0,所以a+b+c>0,故选项B正确不符合题意;
由图象可知,抛物线的最低点为(-2,-1),所以ax2+bx+c≥﹣1,故选项C正确不符合题意;
由图象可知,抛物线的对称轴为x=-2,,所以4a﹣b=0,故选项D错误符合题意.
故选:D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
A.abc<0 B.a+b>m(am+b)(m≠1)
C.4a﹣2b+c<0 D.3a+c=1
【答案】D
【详解】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,故A正确;
当x=m(m≠1)时,y=am2+bm+c,
当x=1时,y有最大值为a+b+c,
∴am2+bm+c<a+b+c,
∴am2+bm<a+b,
∴a+b>m(am+b)(m≠1),故B正确;
由图象知,当x=﹣2时,y<0,
即4a﹣2b+c<0,故C正确;
由图象知,抛物线与x轴的交点横坐标大于﹣1小于0,对称轴为x=1,
∴抛物线与x轴另一交点的横坐标大于2小于3,
∴当x=3时,y<0,
∴9a+3b+c<0,
∵b=﹣2a,
∴3a+c<0,故D错误;
故选:D.
5.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x … 0 1 2 …
… t m n …
且当时,其对应的函数值.有下列结论:
①;②和3是关于x的方程的两个根;③对称轴为;④;其中,正确结论的个数是( )A.0 B.1 C.2 D.3
【答案】C
【详解】二次函数(a,b,c是常数,),
当时,,
当时,,
.
当时,其对应的函数值,
二次函数开口向下,.
,,,
.(①结论符合题意)
时,,
是关于x的方程的根.
对称轴,,(③结论不符合题意)
和3是关于x的方程的两个根.(②结论符合题意)
时,,
时,,
.
.(④结论不符合题意)
正确的结论有2个.
故选:C.
6.已知抛物线(c为常数)经过点,,,当时,则m的取值范围为( )
A. B.
C. D.
【答案】B
【详解】∵过点(4,c),
∴16+4b+c=c,解得b=-4,
∴,
∴则抛物线的对称轴为x=2,,
∵(p,m)和(q,m)的函数值相等,
∴(p,m)和(q,m)关于抛物线对称轴对称,
∴,即,
∵,
∴,解得:,
将点(q,m)代入,
有:,变形得:,
∵函数的自变量范围为,
∴当q=5时,m取最大值,m=c+5,
当q=时,m取最小值,,
∴m的取值范围为:,
故选:B.
7.已知二次函数,当时,函数的最大值为8,则的值是____.
【答案】无解
【详解】解:∵二次函数,
∴二次函数的对称轴为直线,
①当,即时,此时二次函数在上y随x的增大而减小,在取最大值,即,解得,与不符;
②当即时,此时离二次函数对称轴更远,
∴二次函数在取最大值,即,解得,与不符;
③当即时,此时离二次函数对称轴更远,
∴二次函数在取最大值,即,解得与不符;
④当即时,此时二次函数在上y随x的增大而增大,在取最大值,,解得与不符.
综上不存在符合题意的的值.
故答案:无解.
8.若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是____________.
【答案】
【详解】解:点到轴的距离小于2,
,
点在二次函数的图象上,
,
当时,有最小值为1.
当时,,
的取值范围为.
故答案为:
9.已知抛物线的顶点(0,1).
(1)求该抛物线的解析式;
(2)如图1,直线交x轴于A,交抛物线于B、C,BE⊥x轴于E,CF⊥x轴于F,试比较AE AF与4的大小关系.
(3)如图2,D(0,2),M(1,3),抛物线上是否存在点N,使得取得最小值,若存在,求出N的坐标,若不存在,说明理由.
【答案】(1)
(2)AE·AF>4;
(3)N(1,).
【详解】(1)解:将点(0,1)代入,得c=1,
∵点(0,1)是顶点,
∴,
∴b=0,
∴该抛物线的解析式为:;
(2)当y=kx+k=k(x+1)=0(k≠0)时,
解得:x=-1,
∴A( 1,0),
联立,得:,
整理得:,
∴,,
∵AE=,AF=,
∴AE·AF
=
=
=
=,
∴AE·AF>4;
(3)存在点N,使得NM+ND取得最小值,
设抛物线上任意一点H(x,y),
∴HD=,H点到x轴的距离为y,
∵,
∴HD=,
∴H点到D的距离与H点到x轴的距离相等,
∴N点到D的距离与N点到x轴的距离相等,
∴当MN⊥x轴时,MN+ND的值最小,
∴点N的横坐标为1,
当x=1时,,
∴N(1,).
10.北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为,着陆坡顶端与落地点的距离为米,若斜坡的坡度(即.求:
(1)点的坐标;
(2)该抛物线的函数表达式;
(3)起跳点与着陆坡顶端之间的水平距离的长.(精确到米)(参考数据:)
【答案】(1)
(2)
(3)的长约为米
【详解】(1)解:∵,且点在轴正半轴,
∴.
(2)∵抛物线最高点的坐标为,
∴设抛物线的解析式为:,
∵,
∴,
解得.
∴抛物线的解析式为:.
(3)在中,,,
设CE=3x,DE=4x,
∴,
即,
解得x=0.5,
∴,.
点的纵坐标为,
令,
解得,或不合题意,舍去,
∴.
∴.
∴的长约为米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第10课 二次函数y=ax2+bx+c(a≠0)的图象与性质
题组A 基础过关练
1.抛物线经过点(m,3),则代数式的值为( )
A.0 B.1 C.2 D.3
2.二次函数(a≠0)中x,y的部分对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 ﹣4 ﹣6 ﹣6 ﹣4 …
则该二次函数图象的对称轴为( )
A.y轴 B.直线x= C.直线x=1 D.直线x=
3.若二次函数y=x2+2x+k的图象经过点(1,y1),(﹣2,y2),则y1,y2与的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
4.已知(﹣4,y1),(2.5,y2),(5,y3)是抛物线y=﹣3x2﹣6x+m上的点,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y1>y3
5.已知函数y=a﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.若a>0,则当x≥1时,y随x的增大而减小 B.若a<0,则当x≤1时,y随x的增大而增大
C.当a=1时,函数图像过点(﹣1,1) D.当a=﹣2时,函数图像与x轴没有交点
6.已知二次函数的图象如图所示,有以下4个结论:①;②;③;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.已知二次函数y=x2-4x-m的最小值是1,则m=_______.
8.二次函数的图象过点,,若当时.随着的增大而减小,则实数的取值范围是______.
9.已知抛物线y=ax2-2ax-3+2a2 (a<0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求抛物线的函数解析式;
10.已知抛物线.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当为何值时,函数取得最大值,请求出这个最大值.
题组B 能力提升练
1.将二次函数的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为,则、的值为( )
A., B.,
C., D.,
2.如图是二次函数y=ax2﹣x+a2﹣9图象,图象过坐标原点,则a的值是( )
A.a=3 B.a=-3 C.a=-9 D.a=3或a=﹣3
3.已知二次函数,当函数值y随x值的增大而增大时,x的取值范围是( )
A. B. C. D.
4.已知抛物线的最低点的纵坐标为,则抛物线的表达式是( )
A. B. C. D.
5.直线与抛物线在同一平面直角坐标系中的图像可能是( )
A. B. C. D.
6.二次函数()的部分图象如图所示,图象过点(,0),对称轴为直线,下列结论:(1);(2); (3);(4)若点A(,),点B(,),点C(,)在该函数图象上,则;(5)m为任意实数,则.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
7.已知二次函数,当时,自变量的取值范围是______.
8.如图,抛物线的对称轴为直线,点A,B均在抛物线上,且与x轴平行,其中点A的坐标为,则点B的坐标为_____.
9.如图,在平面直角坐标系中,抛物线经过点A(﹣1,0),B(4,0),C(0,﹣2).
(1)求此抛物线的解析式和对称轴.
(2)在此抛物线的对称轴上是否存在点P,使△PAC的周长最小?若存在,请求出点P的坐标;若不存在,说明理由.
10.如图,已知抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,直接写出y的取值范围;
题组C 培优拔尖练
1.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
2.若点A(﹣3,),B(1,),C(m,)在抛物线y=ax2+4ax+c上,且<<,则m的取值范围是( )
A.﹣3<m<1 B.﹣5<m<﹣1或﹣3<m<1
C.m<﹣3或m>1 D.﹣5<m<﹣3或﹣1<m<1
3.二次函数y=ax2+bx+c的大致图象如图,下列结论错误的为( )
A.b2﹣4ac>0 B.a+b+c>0
C.ax2+bx+c≥﹣1 D.2a﹣b=0
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
A.abc<0 B.a+b>m(am+b)(m≠1)
C.4a﹣2b+c<0 D.3a+c=1
5.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x … 0 1 2 …
… t m n …
且当时,其对应的函数值.有下列结论:
①;②和3是关于x的方程的两个根;③对称轴为;④;其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6.已知抛物线(c为常数)经过点,,,当时,则m的取值范围为( )
A. B.
C. D.
7.已知二次函数,当时,函数的最大值为8,则的值是____.
8.若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是____________.
9.已知抛物线的顶点(0,1).
(1)求该抛物线的解析式;
(2)如图1,直线交x轴于A,交抛物线于B、C,BE⊥x轴于E,CF⊥x轴于F,试比较AE AF与4的大小关系.
(3)如图2,D(0,2),M(1,3),抛物线上是否存在点N,使得取得最小值,若存在,求出N的坐标,若不存在,说明理由.
10.北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为,着陆坡顶端与落地点的距离为米,若斜坡的坡度(即.求:
(1)点的坐标;
(2)该抛物线的函数表达式;
(3)起跳点与着陆坡顶端之间的水平距离的长.(精确到米)(参考数据:)
题组A 基础过关练
1.抛物线经过点(m,3),则代数式的值为( )
A.0 B.1 C.2 D.3
【答案】D
【详解】解:将点(m,3)代入中得,
,
故代数式的值为3,
故选:D.
2.二次函数(a≠0)中x,y的部分对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 ﹣4 ﹣6 ﹣6 ﹣4 …
则该二次函数图象的对称轴为( )
A.y轴 B.直线x= C.直线x=1 D.直线x=
【答案】B
【详解】解:由图表可知:
x=0时,y=-6,
x=1时,y=-6,
∴二次函数的对称轴为:,
故选:B.
3.若二次函数y=x2+2x+k的图象经过点(1,y1),(﹣2,y2),则y1,y2与的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
【答案】A
【详解】解:当x=1时,y1=x2+2x+k=1+2+k=k+3;
当x=﹣2时,y2=x2+2x+k=4﹣4+k=k,
所以y1>y2.
故选:A.
4.已知(﹣4,y1),(2.5,y2),(5,y3)是抛物线y=﹣3x2﹣6x+m上的点,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y1>y3
【答案】A
【详解】解:∵y=﹣3x2﹣6x+m,
∴抛物线开口向下,对称轴为直线x=﹣=﹣1,
∴与直线x=﹣1距离越近的点的纵坐标越大,
∵﹣1﹣(﹣4)<2.5﹣(﹣1)<5﹣(﹣1),
∴y1>y2>y3,
故选:A.
5.已知函数y=a﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.若a>0,则当x≥1时,y随x的增大而减小 B.若a<0,则当x≤1时,y随x的增大而增大
C.当a=1时,函数图像过点(﹣1,1) D.当a=﹣2时,函数图像与x轴没有交点
【答案】B
【详解】解:A、抛物线的对称轴为直线:,则若a>0,则当x≥1时,y随x的增大而增大,选项说法错误,不符合题意;
B、抛物线的对称轴为直线:,若a<0,则当x≤1时,y随x的增大而增大,选项说法正确,符合题意;
C、当,时,,则当a=1时,函数图像不经过点(﹣1,1),选项说法错误,不符合题意;
D、当a=﹣2时,,,则函数图像与x轴有两个交点,选项说法错误,不符合题意;
故选B.
6.已知二次函数的图象如图所示,有以下4个结论:①;②;③;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【详解】解:①抛物线开口向下,
,
∵,
∴,
,
抛物线与轴的交点在轴的正半轴,
,
,故错误;
②观察函数图象,可知:
当时,,
,故错误.
③抛物线的对称轴为,抛物线与轴的交点在轴的正半轴,
当时,,
,故正确;
④抛物线与轴有2个交点,
△,故正确.
故选:B.
7.已知二次函数y=x2-4x-m的最小值是1,则m=_______.
【答案】-5
【详解】解:由知,
当x=2时,y有最小值为-4-m,
∵该函数的最小值为1,
∴-4-m=1,
解得:m=-5,
故答案为:-5.
8.二次函数的图象过点,,若当时.随着的增大而减小,则实数的取值范围是______.
【答案】且
【详解】解:将代入得①,
将代入得②,
由②①得,
,,
抛物线的对称轴为直线,
当时.随着的增大而减小,
时,,
解得,
时,,
解得,
故答案为:且.
9.已知抛物线y=ax2-2ax-3+2a2 (a<0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求抛物线的函数解析式;
【答案】(1)x=1
(2)y=-x2+2x-1
【详解】(1)解:∵抛物线,
∴抛物线的对称轴为直线x=1;
(2)由(1)可得,
∵抛物线的顶点在x轴上,
∴,
解得,=-1,
∵a<0,
∴a=-1,
∴抛物线的解析式为.
10.已知抛物线.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当为何值时,函数取得最大值,请求出这个最大值.
【答案】(1)抛物线开口向下,对称轴是直线,顶点坐标是
(2)当时,函数取得最大值,最大值是3.
【详解】(1)解:∵-1<0,
∴抛物线开口向下,
对称轴是直线,
∵,
∴顶点坐标是;
(2)∵抛物线的顶点坐标是,
∴当时,函数取得最大值,最大值是3.
题组B 能力提升练
1.将二次函数的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为,则、的值为( )
A., B.,
C., D.,
【答案】D
【详解】由题意可得新抛物线的顶点为,
∴原抛物线的顶点为,
设原抛物线的解析式为,
代入得:,
∴,.
故选:D.
2.如图是二次函数y=ax2﹣x+a2﹣9图象,图象过坐标原点,则a的值是( )
A.a=3 B.a=-3 C.a=-9 D.a=3或a=﹣3
【答案】A
【详解】解:∵抛物线经过原点,
∴a2-9=0, 解得a=3或a=-3,
∵抛物线开口向上,
∴a=3,
故选:A.
3.已知二次函数,当函数值y随x值的增大而增大时,x的取值范围是( )
A. B. C. D.
【答案】B
【详解】解:∵
∵开口向上,对称轴为x=1,
∴x>1时,函数值y随x的增大而增大.
故选:B.
4.已知抛物线的最低点的纵坐标为,则抛物线的表达式是( )
A. B. C. D.
【答案】B
【详解】解:∵抛物线的最低点的纵坐标为,
∴,
即
∴,
当m=1时,抛物线为.
故选:B.
5.直线与抛物线在同一平面直角坐标系中的图像可能是( )
A. B. C. D.
【答案】B
【详解】解:A、由抛物线可知,a>0,b<0,c>0,则ac>0,由直线可知,ac>0,b>0,故本选项不合题意;
B、由抛物线可知,a>0,b>0,c>0,则ac>0,由直线可知,ac>0,b>0,故本选项符合题意;
C、由抛物线可知,a<0,b<0,c>0,则ac<0,由直线可知,ac>0,b>0,故本选项不合题意;
D、由抛物线可知,a<0,b>0,c>0,则ac<0,由直线可知,ac<0,b<0,故本选项不合题意.
故选:B.
6.二次函数()的部分图象如图所示,图象过点(,0),对称轴为直线,下列结论:(1); (2); (3);(4)若点A(,),点B(,),点C(,)在该函数图象上,则;(5)m为任意实数,则.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
【答案】A
【详解】解:∵对称轴为直线x=2,
∴-=2,
∴b=-4a,
∴b+4a=0,
∴(1)正确;
∵经过点(-1,0),
∴a-b+c=0,
∴c=b-a=-4a-a=-5a,
∴4a+c-2b=4a-5a+8a=7a,
∵a<0,
∴4a+c-2b<0,
∴4a+c<2b,
∴(2)不正确;
∵5a+3c=5a-15a=-10a>0,
∴(3)正确;
∵|-2-2|=4,|-2|=,|-2|=,
∴y1<y2<y3,
∴(4)不正确;
当x=2时,函数有最大值4a+2b+c,
∴am2+bm+c≤4a+2b+c,
∴(5)不正确;
综上所述:(1)(3)正确,
故选:A.
7.已知二次函数,当时,自变量的取值范围是______.
【答案】x≤-2或x≥4
【详解】解:∵二次函数,
∴抛物线开口向上,对称轴为直线,
∴当时,y随x的增大而减小,当时,y随x的增大而增大,
当时,则,
即,
解得,或,
∴当时,自变量x的取值范围是或,
故答案为:或.
8.如图,抛物线的对称轴为直线,点A,B均在抛物线上,且与x轴平行,其中点A的坐标为,则点B的坐标为_____.
【答案】(6,5)
【详解】∵AB与x轴平行,
而点A,B均在抛物线上,
∴点A与点B关于直线x=1对称,
∵点A的坐标为,
∴B点坐标为,
故答案为.
9.如图,在平面直角坐标系中,抛物线经过点A(﹣1,0),B(4,0),C(0,﹣2).
(1)求此抛物线的解析式和对称轴.
(2)在此抛物线的对称轴上是否存在点P,使△PAC的周长最小?若存在,请求出点P的坐标;若不存在,说明理由.
【答案】(1)y=x2﹣x﹣2;对称轴为x=
(2)存在,P的坐标为(,﹣)
【详解】(1)解:设该抛物线的解析式为y=ax2+bx+c,
∵该抛物线过点A(﹣1,0),B(4,0),C(0,﹣2),代入,得:
解得:
∴此抛物线的解析式为y=x2﹣x﹣2.
∵抛物线解析式为y=x2﹣x﹣2=﹣
∴抛物线的对称轴为x= .
(2)解:存在,理由如下:
连接PB
由抛物线的对称性得:PA=PB
∴△PAC的周长PA+PC+AC=PB+PC+AC,
∴当B、P、C三点共线时,PB+PC最小,
即当B、P、C三点共线时,△PAC的周长最小,
设直线BC的解析式为y=kx+m,
将点B(4,0),点C(0,﹣2)代入,
得,解得:,
即直线BC的解析式为y=x﹣2.
令x=,则有y=﹣2=﹣,
即点P的坐标为(,﹣).
∴在此抛物线的对称轴上存在点P,使△PAC的周长最小,此时点P的坐标为(,﹣).
10.如图,已知抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,直接写出y的取值范围;
【答案】(1),顶点坐标为(1,4);
(2)0<y≤4
【详解】(1)解:将A( 1,0)和B(3,0)代入y= x2+bx+c,得,解得:,∴抛物线的解析式为:,∵,∴抛物线的顶点坐标为(1,4);
(2)∵当x=1时,y=4;当x=3时,y=0,∴由函数图象可得:当0<x<3时,0<y≤4.
题组C 培优拔尖练
1.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
【答案】D
【详解】解:∵二次函数图象开口方向向下,
∴a<0,
∵对称轴为直线>0,
∴b>0,
∵与y轴的负半轴相交,
∴c<0,
∴y=bx+c的图象经过第一、三、四象限,
反比例函数y=图象在第二四象限,
只有D选项图象符合.
故选:D.
2.若点A(﹣3,),B(1,),C(m,)在抛物线y=ax2+4ax+c上,且<<,则m的取值范围是( )
A.﹣3<m<1 B.﹣5<m<﹣1或﹣3<m<1
C.m<﹣3或m>1 D.﹣5<m<﹣3或﹣1<m<1
【答案】D
【详解】解:抛物线y=ax2+4ax+c的对称轴为x=﹣=﹣2,
∵点A(﹣3,y1),B(1,y2),C(m,y3)在抛物线y=ax2+4ax+c上,且y1<y3<y2,
∴当a<0,则|m+2|<1且|m+2|>3,(不存在);
当a>0,则1<|m+2|<3,解得﹣5<m<﹣3或﹣1<m<1.
故选:D.
3.二次函数y=ax2+bx+c的大致图象如图,下列结论错误的为( )
A.b2﹣4ac>0 B.a+b+c>0
C.ax2+bx+c≥﹣1 D.2a﹣b=0
【答案】D
【详解】解:由图象可知,抛物线与x轴有两个交点,所以b2﹣4ac>0,故选项A正确不符合题意;
由图象可知,当x=1时,y>0,所以a+b+c>0,故选项B正确不符合题意;
由图象可知,抛物线的最低点为(-2,-1),所以ax2+bx+c≥﹣1,故选项C正确不符合题意;
由图象可知,抛物线的对称轴为x=-2,,所以4a﹣b=0,故选项D错误符合题意.
故选:D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
A.abc<0 B.a+b>m(am+b)(m≠1)
C.4a﹣2b+c<0 D.3a+c=1
【答案】D
【详解】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,故A正确;
当x=m(m≠1)时,y=am2+bm+c,
当x=1时,y有最大值为a+b+c,
∴am2+bm+c<a+b+c,
∴am2+bm<a+b,
∴a+b>m(am+b)(m≠1),故B正确;
由图象知,当x=﹣2时,y<0,
即4a﹣2b+c<0,故C正确;
由图象知,抛物线与x轴的交点横坐标大于﹣1小于0,对称轴为x=1,
∴抛物线与x轴另一交点的横坐标大于2小于3,
∴当x=3时,y<0,
∴9a+3b+c<0,
∵b=﹣2a,
∴3a+c<0,故D错误;
故选:D.
5.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x … 0 1 2 …
… t m n …
且当时,其对应的函数值.有下列结论:
①;②和3是关于x的方程的两个根;③对称轴为;④;其中,正确结论的个数是( )A.0 B.1 C.2 D.3
【答案】C
【详解】二次函数(a,b,c是常数,),
当时,,
当时,,
.
当时,其对应的函数值,
二次函数开口向下,.
,,,
.(①结论符合题意)
时,,
是关于x的方程的根.
对称轴,,(③结论不符合题意)
和3是关于x的方程的两个根.(②结论符合题意)
时,,
时,,
.
.(④结论不符合题意)
正确的结论有2个.
故选:C.
6.已知抛物线(c为常数)经过点,,,当时,则m的取值范围为( )
A. B.
C. D.
【答案】B
【详解】∵过点(4,c),
∴16+4b+c=c,解得b=-4,
∴,
∴则抛物线的对称轴为x=2,,
∵(p,m)和(q,m)的函数值相等,
∴(p,m)和(q,m)关于抛物线对称轴对称,
∴,即,
∵,
∴,解得:,
将点(q,m)代入,
有:,变形得:,
∵函数的自变量范围为,
∴当q=5时,m取最大值,m=c+5,
当q=时,m取最小值,,
∴m的取值范围为:,
故选:B.
7.已知二次函数,当时,函数的最大值为8,则的值是____.
【答案】无解
【详解】解:∵二次函数,
∴二次函数的对称轴为直线,
①当,即时,此时二次函数在上y随x的增大而减小,在取最大值,即,解得,与不符;
②当即时,此时离二次函数对称轴更远,
∴二次函数在取最大值,即,解得,与不符;
③当即时,此时离二次函数对称轴更远,
∴二次函数在取最大值,即,解得与不符;
④当即时,此时二次函数在上y随x的增大而增大,在取最大值,,解得与不符.
综上不存在符合题意的的值.
故答案:无解.
8.若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是____________.
【答案】
【详解】解:点到轴的距离小于2,
,
点在二次函数的图象上,
,
当时,有最小值为1.
当时,,
的取值范围为.
故答案为:
9.已知抛物线的顶点(0,1).
(1)求该抛物线的解析式;
(2)如图1,直线交x轴于A,交抛物线于B、C,BE⊥x轴于E,CF⊥x轴于F,试比较AE AF与4的大小关系.
(3)如图2,D(0,2),M(1,3),抛物线上是否存在点N,使得取得最小值,若存在,求出N的坐标,若不存在,说明理由.
【答案】(1)
(2)AE·AF>4;
(3)N(1,).
【详解】(1)解:将点(0,1)代入,得c=1,
∵点(0,1)是顶点,
∴,
∴b=0,
∴该抛物线的解析式为:;
(2)当y=kx+k=k(x+1)=0(k≠0)时,
解得:x=-1,
∴A( 1,0),
联立,得:,
整理得:,
∴,,
∵AE=,AF=,
∴AE·AF
=
=
=
=,
∴AE·AF>4;
(3)存在点N,使得NM+ND取得最小值,
设抛物线上任意一点H(x,y),
∴HD=,H点到x轴的距离为y,
∵,
∴HD=,
∴H点到D的距离与H点到x轴的距离相等,
∴N点到D的距离与N点到x轴的距离相等,
∴当MN⊥x轴时,MN+ND的值最小,
∴点N的横坐标为1,
当x=1时,,
∴N(1,).
10.北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为,着陆坡顶端与落地点的距离为米,若斜坡的坡度(即.求:
(1)点的坐标;
(2)该抛物线的函数表达式;
(3)起跳点与着陆坡顶端之间的水平距离的长.(精确到米)(参考数据:)
【答案】(1)
(2)
(3)的长约为米
【详解】(1)解:∵,且点在轴正半轴,
∴.
(2)∵抛物线最高点的坐标为,
∴设抛物线的解析式为:,
∵,
∴,
解得.
∴抛物线的解析式为:.
(3)在中,,,
设CE=3x,DE=4x,
∴,
即,
解得x=0.5,
∴,.
点的纵坐标为,
令,
解得,或不合题意,舍去,
∴.
∴.
∴的长约为米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
