3.2代数式 冀教版(2024)初中数学七年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 3.2代数式 冀教版(2024)初中数学七年级上册同步练习(含详细答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 476.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 19:42:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.2代数式冀教版( 2024)初中数学七年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.请仔细分析下列赋予实际意义的例子,其中错误的是( )
A. 若表示一个正方形的边长,则表示这个正方形的周长
B. 若一个两位数的十位数字是,个位数字是,则表示这个两位数
C. 若阳光玫瑰的价格是元千克,则表示购买千克该种阳光玫瑰的金额
D. 若一辆汽车行驶速度是千米小时,则表示这辆汽车行驶小时的路程
2.用代数式表示“的倍与的相反数的和”,下列不正确的是( )
A. B. C. D.
3.分形的概念是由数学家本华曼德博提出的.如图是分形的一种,第个图案有个三角形;第个图案有个三角形;第个图案有个三角形;第个图案有个三角形;下列数据中是按此规律分形得到的三角形的个数是( )
A. B. C. D.
4.某商场举行促销活动,促销的方法是“消费超过元时,所购买的商品按原价打折后,再减少元”若某商品的原价为元,则购买该商品实际付款的金额是 ( )
A. 元 B. 元 C. 元 D. 元
5.去年李华妈妈的年龄是岁,李华比妈妈小岁,那么李华今年的年龄是( )
A. 岁 B. 岁 C. 岁 D. 岁
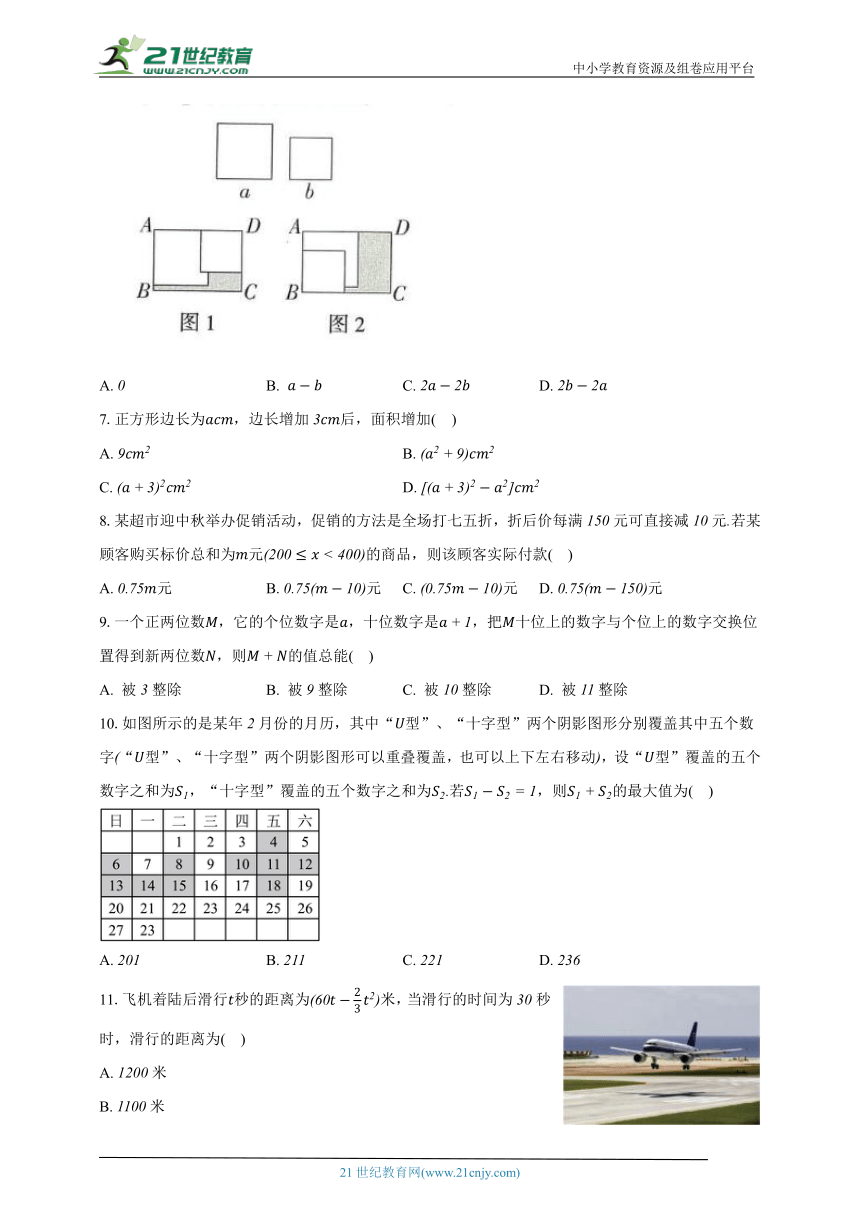
6.将两个边长分别为和的正方形纸片按图、图两种方式置于长方形中图、图中两张正方形纸片均有部分重叠,长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图中阴影部分的周长为,图中阴影部分的周长为,则的值为( )
A. B. C. D.
7.正方形边长为,边长增加后,面积增加( )
A. B.
C. D.
8.某超市迎中秋举办促销活动,促销的方法是全场打七五折,折后价每满元可直接减元若某顾客购买标价总和为元的商品,则该顾客实际付款( )
A. 元 B. 元 C. 元 D. 元
9.一个正两位数,它的个位数字是,十位数字是,把十位上的数字与个位上的数字交换位置得到新两位数,则的值总能( )
A. 被整除 B. 被整除 C. 被整除 D. 被整除
10.如图所示的是某年月份的月历,其中“型”、“十字型”两个阴影图形分别覆盖其中五个数字“型”、“十字型”两个阴影图形可以重叠覆盖,也可以上下左右移动,设“型”覆盖的五个数字之和为,“十字型”覆盖的五个数字之和为若,则的最大值为( )
A. B. C. D.
11.飞机着陆后滑行秒的距离为米,当滑行的时间为秒时,滑行的距离为( )
A. 米
B. 米
C. 米
D. 米
12.若桶油漆可以刷的墙,则桶油漆可以刷的墙.
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.小明下五子棋的时候,用棋子按一定的规律摆了如下三个图形,请你猜测一下,若小明继续摆下去,第个图形需要______颗棋子用含的代数式表示
14.某服装以单价元的价格购进一批服装,加价进行销售,把最后一件服装按售价的八折售完,则最后一件服装的售价是______元用含有的代数式表示
15.按规定,食品包装袋上都应标明袋内装有食品多少克,如表是、、、四种饼干的检验结果,“、”分别表示比标准重量多和少,用绝对值判断最符合标准的一种食品是______填写饼干型号
16.如图,在中,,于,点在上,在内部,且满足,,交于,若,,则的长为______用含字母的代数式表示
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
点为数轴的原点,点、在数轴上的位置如图所示,点表示的数为,、两点间的距离是点到原点间距离的倍点在数轴上,点到、两点间的距离相等.
求点表示的数;
若、两点间的距离为,求点到原点的距离;
若、两点间的距离为,求、两点间的距离用含的代数式表示
18.本小题分
某商店原有袋大米,每袋大米为,上午售出袋,下午又购进同样包装的大米袋进货后这个商店有大米多少千克
19.本小题分
观察下列现象:;;;;;
以上每个等式中两边数字是对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
根据上面各式反映的规律填空,使式子成为“数字对称等式”.
______ ______;
______ ______;
______ ______.
设这类等式左边两位数的十位数字为,个位数字为,且,请你用含,式子表示“数字对称等式”的一般形式;
证明你在中写出的等式的正确性.
20.本小题分
观察下列三行数:
,,,,
,,,,
,,,,
第行的第个数是______;
若第行某列的数是,则第行该列的数是______,第行该列的数是______;
设,,是每行的第个数,计算的值.
21.本小题分
把形状、大小完全相同的小长方形卡片如图不重叠地放在一个底面为长方形长为,宽为,且的盒子底部,有如下两种摆法如图,盒子底部未被卡片覆盖的部分用阴影表示.
图中阴影部分的周长为______用含,的式子表示;
图中,若,请直接写出,的长用含,的式子表示;
若图中阴影部分的面积为,,且,在的条件下,求图中的长.
22.本小题分
随着农业技术的现代化,节水型灌溉得到逐步推广喷灌和滴灌是比漫灌节水的灌溉方式,灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的和,设第一块实验田用水量吨.
根据第一块实验田的用水量吨,分别表示出另两块实验田的用水量;
如果第三块实验田用水吨,则另两块实验田共用水多少吨?
如果三块实验田的用水总量是第二块实验田和第三块实验田用水量的两倍还多吨,则每块实验田各用水多少吨?
答案和解析
1.【答案】
【解析】【分析】
本题主要考查代数式,解题的关键是掌握代数式的书写规范和实际问题中数量间的关系.
根据代数式表示实际意义的方法分别判断每个选项即可得.
【解答】
解:、若表示个正方形的边长,则表示这个正方形的周长,这个说法正确,不符合题意;
B、若和分别表示一个两位数中的十位数和个位数字,则表示这个两位数,
这个说法没有实际意义,是不正确的,符合题意;
C、阳光玫瑰的价格是元千克,则表示购买千克该种阳光玫瑰的金额这个说法正确,不符合题意;
D、一辆汽车的行驶速度是千米小时,则表示这辆汽车行驶小时的路程,这个说法正确,不符合题意;
故选B.
2.【答案】
【解析】【分析】
本题考查列代数式.根据题意,可以用含、的代数式表示出的倍与的相反数的和.
【解答】
解:的倍与的相反数的和可以表示为:,
故不正确的是选项.
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】解:去年李华妈妈岁,
李华妈妈今年的年龄是岁,
李华比妈妈小岁,
李华今年的年龄是:岁.
故选:.
直接表示出李华妈妈今年的岁数,再利用李华比妈妈小岁表示出李华今年的年龄.
此题主要考查了列代数式,正确表示出李华妈妈今年的年龄是解题关键.
6.【答案】
【解析】由题意知,
因为四边形是长方形,
所以,.
所以,
同理,,
故故选A.
7.【答案】
【解析】【分析】
此题考查了列代数式,用到的知识点是正方形的面积公式,分别求出两次正方形的面积,再进行比较是本题的关键.
先求出正方形边长为的面积,再求出边长增加后的面积,最后进行相减,即可得出答案.
【解答】
解:正方形边长为,
它的面积是;
边长增加后,
它的面积是,
面积增加;
故选D.
8.【答案】
【解析】解:购买商品的标价总和:,
当为最少时,折后价:元,
在折后价再减元,
实际付款:元,
故选:.
先用字母表示出打折后付的钱数,再根据题意表示出实际付款的代数式.
本题考查了在实际问题中列代数式,关键分析出打折后还能优惠的钱.
9.【答案】
【解析】解:由题意,
,
的值总能被整除;
故选:.
求出的值,因式分解后,进行判断即可.
本题考查整式的加减运算,熟练掌握因式分解是关键.
10.【答案】
【解析】【分析】
本题考查了代数式的知识点,熟练掌握以上知识点是解题的关键.
根据日历中的规律可表示出“型”夏盖的五个数字和“十字型”覆盖的五个数字,从而表示出,,由,整理可得,结合,的取值范围即可获得答案.
【解答】
解:
.
,
,
当最大时也取得最大值,
由月历图知,的最大值为,
所以的最大值为
11.【答案】
【解析】解:当时,,
即滑行的距离为米.
故选:.
把代入式子,即可解答.
本题考查代数式求值,熟练掌握代数式求值是解题的关键.
12.【答案】
【解析】【分析】根据题意先求出桶油漆可以刷墙的面积,再乘列出代数式即可求解.
【解答】解:
故选:.
【点评】此题考查列代数式问题,关键根据题意列出代数式解答.
13.【答案】
【解析】解:第个图形中棋子的个数是,
第个图形中棋子的个数是,
第个图形中棋子的个数是,
,
第个图形中棋子的个数是.
故选:.
根据前三个图形中棋子的数量,可找出变化规律“”.
本题考查了规律型:图形的变化类.发现规律是关键.
14.【答案】
【解析】解:根据题意,得元.
故答案为:.
加价后的价格为元,打折后的售价为元.
此题主要考查了列代数式,正确表示出商品的售价和成本是解题关键.
15.【答案】
【解析】解:,
故D饼干最符合标准.
故答案为:.
根据绝对值越小越符合标准即可得到答案.
本题主要考查了绝对值、列代数式,掌握绝对值越小越符合标准是解题的关键.
16.【答案】
【解析】解:,,
是等边三角形,
,,
,
,
,
在中,,
,
,
.
故答案为:.
依题意得是等边三角形,则,根据等腰三角形性质得,,则,进而得,然后再根据即可得出的长.
此题主要考查了等边三角形的性质,列代数式,等腰三角形的性质,熟练掌握等边三角形的性质,等腰三角形的性质是解决问题的关键.
17.【答案】解:设点表示的数为,根据题意得:
,
解得.
即点表示的数为.
故答案为:;
设点表示的数为,根据题意得:
,
解得或,
点到点的距离为或;
设点表示的数为,根据题意得:
,
解得或,
当时,
点到、两点的距离相等,
表示的数是,
点到点的距离为,
当时,
同理点到点的距离为,
点到点的距离是或.
【解析】设点表示的数为,根据点到点的距离是点到点距离的倍列出方程,求解即可;
设点表示的数为,根据点到点的距离为列出方程,求出,进而得到点到点的距离;
设点表示的数为,根据点到点的距离为,求出,进而得到点到点的距离.
本题考查一元一次方程的应用,数轴上的有理数,两点间的距离,解题的关键是用含字母的式子表示相关点表示的数及分类讨论思想的应用.
18.【答案】解:根据题意得:
故进货后这个商店有大米千克.
【解析】本题考查了整式的加减,解题的关键是根据题意列出算式,计算比较简单.
根据数量关系式计算,原来大米总重量上午卖出的重量下午购进的重量剩下的重量.
19.【答案】
【解析】解:对称到,对称到,
.
故答案为:,.
对称到,,得左边第个乘数为,
对称到,
.
故答案为:,.
中的对称到,得左边第个乘数为,
对称到,
.
故答案为:,.
.
证明:,
得证.
先找出数字对称的规律,以及数字之和的规律即可填空,再正确地列出等式证明即可.
本题主要考查学生寻找数字对称的规律,以及数字之和的规律的能力,正确地列出等式并证明是难点.
20.【答案】
【解析】解:,,,,
第行的第个数是,
故答案为:;
,,,,
第行的第个数是;
,,,,
第行的第个数是;
第行的第个数是,
第行的每一个数是第行的每一个数的,第行的每一个数是第行的每一个数的倍再加上,
若第行某列的数是,则第行该列的数是,第行该列的数是,
故答案为:,;
,,是每行的第个数,
,,,
.
根据,,,可以得出第行的第个数是,得到答案;
计算得出第行的第个数是,第行的第个数是,从而得出第行的每一个数是第行的每一个数的,第行的每一个数是第行的每一个数的倍再加上,由此即可得到答案;
先计算出、、的值,再代入进行计算即可得到答案.
本题考查数字的变化类规律探究、有理数的四则混合运算,根据题意得出第行的第个数是,第行的第个数是,第行的第个数是是解此题的关键.
21.【答案】
【解析】解:如图.
阴影部分的周长为.
故答案为:.
由图,得,.
图中阴影部分的面积为,
,
,
,
,
根据题意,得图中阴影部分的面积也是,
,
将、和代入,得,
将代入,得,
,
,
,
解得,
.
利用割补法计算即可;
根据图中、与和的数量关系作答即可;
图和中阴影部分的面积均为,据此得到、、、之间的数量关系,求出、,进而求出、,再由计算的长即可.
本题考查整式的混合运算、列代数式,根据几何图形长度之间的数量关系列代数式是解题的关键.
22.【答案】解:第二块实验田用水量表示为吨,第三块实验田用水量表示为吨;
已知第三块实验田用水量表示为:吨,
由题意列方程为:,
解得,
即第一块实验田用水量为吨,
则第二块实验田用水量为:,
第一块实验田和第二块实验田共用水: 吨,
答:另两块实验田共用水吨;
根据已知条件可列方程:,
解得:,
所以第一块实验田用水量为吨,
第二块实验田用水量为:吨,
第三块实验田用水量为:吨,
答:第一块实验田用水量为吨,第二块实验田用水量为吨,第三块实验田用水量为吨.
【解析】根据后两种方式用水量分别是漫灌的和,可分别求出另两块实验田的用水量;
根据第三块实验田用水吨,可以列方程,解出,再分别求另两块用水量,即可求出另两块实验田共用水量;
根据三块实验田的用水总量是第二块实验田和第三块实验田用水量的两倍还多吨,可列方程,解出,再分别求另两块用水量即可.
本题考查了一元一次方程的应用,列代数式,解题关键是弄清题意,找出等量关系,并根据等量关系列方程,再求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.2代数式冀教版( 2024)初中数学七年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.请仔细分析下列赋予实际意义的例子,其中错误的是( )
A. 若表示一个正方形的边长,则表示这个正方形的周长
B. 若一个两位数的十位数字是,个位数字是,则表示这个两位数
C. 若阳光玫瑰的价格是元千克,则表示购买千克该种阳光玫瑰的金额
D. 若一辆汽车行驶速度是千米小时,则表示这辆汽车行驶小时的路程
2.用代数式表示“的倍与的相反数的和”,下列不正确的是( )
A. B. C. D.
3.分形的概念是由数学家本华曼德博提出的.如图是分形的一种,第个图案有个三角形;第个图案有个三角形;第个图案有个三角形;第个图案有个三角形;下列数据中是按此规律分形得到的三角形的个数是( )
A. B. C. D.
4.某商场举行促销活动,促销的方法是“消费超过元时,所购买的商品按原价打折后,再减少元”若某商品的原价为元,则购买该商品实际付款的金额是 ( )
A. 元 B. 元 C. 元 D. 元
5.去年李华妈妈的年龄是岁,李华比妈妈小岁,那么李华今年的年龄是( )
A. 岁 B. 岁 C. 岁 D. 岁
6.将两个边长分别为和的正方形纸片按图、图两种方式置于长方形中图、图中两张正方形纸片均有部分重叠,长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图中阴影部分的周长为,图中阴影部分的周长为,则的值为( )
A. B. C. D.
7.正方形边长为,边长增加后,面积增加( )
A. B.
C. D.
8.某超市迎中秋举办促销活动,促销的方法是全场打七五折,折后价每满元可直接减元若某顾客购买标价总和为元的商品,则该顾客实际付款( )
A. 元 B. 元 C. 元 D. 元
9.一个正两位数,它的个位数字是,十位数字是,把十位上的数字与个位上的数字交换位置得到新两位数,则的值总能( )
A. 被整除 B. 被整除 C. 被整除 D. 被整除
10.如图所示的是某年月份的月历,其中“型”、“十字型”两个阴影图形分别覆盖其中五个数字“型”、“十字型”两个阴影图形可以重叠覆盖,也可以上下左右移动,设“型”覆盖的五个数字之和为,“十字型”覆盖的五个数字之和为若,则的最大值为( )
A. B. C. D.
11.飞机着陆后滑行秒的距离为米,当滑行的时间为秒时,滑行的距离为( )
A. 米
B. 米
C. 米
D. 米
12.若桶油漆可以刷的墙,则桶油漆可以刷的墙.
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.小明下五子棋的时候,用棋子按一定的规律摆了如下三个图形,请你猜测一下,若小明继续摆下去,第个图形需要______颗棋子用含的代数式表示
14.某服装以单价元的价格购进一批服装,加价进行销售,把最后一件服装按售价的八折售完,则最后一件服装的售价是______元用含有的代数式表示
15.按规定,食品包装袋上都应标明袋内装有食品多少克,如表是、、、四种饼干的检验结果,“、”分别表示比标准重量多和少,用绝对值判断最符合标准的一种食品是______填写饼干型号
16.如图,在中,,于,点在上,在内部,且满足,,交于,若,,则的长为______用含字母的代数式表示
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
点为数轴的原点,点、在数轴上的位置如图所示,点表示的数为,、两点间的距离是点到原点间距离的倍点在数轴上,点到、两点间的距离相等.
求点表示的数;
若、两点间的距离为,求点到原点的距离;
若、两点间的距离为,求、两点间的距离用含的代数式表示
18.本小题分
某商店原有袋大米,每袋大米为,上午售出袋,下午又购进同样包装的大米袋进货后这个商店有大米多少千克
19.本小题分
观察下列现象:;;;;;
以上每个等式中两边数字是对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
根据上面各式反映的规律填空,使式子成为“数字对称等式”.
______ ______;
______ ______;
______ ______.
设这类等式左边两位数的十位数字为,个位数字为,且,请你用含,式子表示“数字对称等式”的一般形式;
证明你在中写出的等式的正确性.
20.本小题分
观察下列三行数:
,,,,
,,,,
,,,,
第行的第个数是______;
若第行某列的数是,则第行该列的数是______,第行该列的数是______;
设,,是每行的第个数,计算的值.
21.本小题分
把形状、大小完全相同的小长方形卡片如图不重叠地放在一个底面为长方形长为,宽为,且的盒子底部,有如下两种摆法如图,盒子底部未被卡片覆盖的部分用阴影表示.
图中阴影部分的周长为______用含,的式子表示;
图中,若,请直接写出,的长用含,的式子表示;
若图中阴影部分的面积为,,且,在的条件下,求图中的长.
22.本小题分
随着农业技术的现代化,节水型灌溉得到逐步推广喷灌和滴灌是比漫灌节水的灌溉方式,灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的和,设第一块实验田用水量吨.
根据第一块实验田的用水量吨,分别表示出另两块实验田的用水量;
如果第三块实验田用水吨,则另两块实验田共用水多少吨?
如果三块实验田的用水总量是第二块实验田和第三块实验田用水量的两倍还多吨,则每块实验田各用水多少吨?
答案和解析
1.【答案】
【解析】【分析】
本题主要考查代数式,解题的关键是掌握代数式的书写规范和实际问题中数量间的关系.
根据代数式表示实际意义的方法分别判断每个选项即可得.
【解答】
解:、若表示个正方形的边长,则表示这个正方形的周长,这个说法正确,不符合题意;
B、若和分别表示一个两位数中的十位数和个位数字,则表示这个两位数,
这个说法没有实际意义,是不正确的,符合题意;
C、阳光玫瑰的价格是元千克,则表示购买千克该种阳光玫瑰的金额这个说法正确,不符合题意;
D、一辆汽车的行驶速度是千米小时,则表示这辆汽车行驶小时的路程,这个说法正确,不符合题意;
故选B.
2.【答案】
【解析】【分析】
本题考查列代数式.根据题意,可以用含、的代数式表示出的倍与的相反数的和.
【解答】
解:的倍与的相反数的和可以表示为:,
故不正确的是选项.
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】解:去年李华妈妈岁,
李华妈妈今年的年龄是岁,
李华比妈妈小岁,
李华今年的年龄是:岁.
故选:.
直接表示出李华妈妈今年的岁数,再利用李华比妈妈小岁表示出李华今年的年龄.
此题主要考查了列代数式,正确表示出李华妈妈今年的年龄是解题关键.
6.【答案】
【解析】由题意知,
因为四边形是长方形,
所以,.
所以,
同理,,
故故选A.
7.【答案】
【解析】【分析】
此题考查了列代数式,用到的知识点是正方形的面积公式,分别求出两次正方形的面积,再进行比较是本题的关键.
先求出正方形边长为的面积,再求出边长增加后的面积,最后进行相减,即可得出答案.
【解答】
解:正方形边长为,
它的面积是;
边长增加后,
它的面积是,
面积增加;
故选D.
8.【答案】
【解析】解:购买商品的标价总和:,
当为最少时,折后价:元,
在折后价再减元,
实际付款:元,
故选:.
先用字母表示出打折后付的钱数,再根据题意表示出实际付款的代数式.
本题考查了在实际问题中列代数式,关键分析出打折后还能优惠的钱.
9.【答案】
【解析】解:由题意,
,
的值总能被整除;
故选:.
求出的值,因式分解后,进行判断即可.
本题考查整式的加减运算,熟练掌握因式分解是关键.
10.【答案】
【解析】【分析】
本题考查了代数式的知识点,熟练掌握以上知识点是解题的关键.
根据日历中的规律可表示出“型”夏盖的五个数字和“十字型”覆盖的五个数字,从而表示出,,由,整理可得,结合,的取值范围即可获得答案.
【解答】
解:
.
,
,
当最大时也取得最大值,
由月历图知,的最大值为,
所以的最大值为
11.【答案】
【解析】解:当时,,
即滑行的距离为米.
故选:.
把代入式子,即可解答.
本题考查代数式求值,熟练掌握代数式求值是解题的关键.
12.【答案】
【解析】【分析】根据题意先求出桶油漆可以刷墙的面积,再乘列出代数式即可求解.
【解答】解:
故选:.
【点评】此题考查列代数式问题,关键根据题意列出代数式解答.
13.【答案】
【解析】解:第个图形中棋子的个数是,
第个图形中棋子的个数是,
第个图形中棋子的个数是,
,
第个图形中棋子的个数是.
故选:.
根据前三个图形中棋子的数量,可找出变化规律“”.
本题考查了规律型:图形的变化类.发现规律是关键.
14.【答案】
【解析】解:根据题意,得元.
故答案为:.
加价后的价格为元,打折后的售价为元.
此题主要考查了列代数式,正确表示出商品的售价和成本是解题关键.
15.【答案】
【解析】解:,
故D饼干最符合标准.
故答案为:.
根据绝对值越小越符合标准即可得到答案.
本题主要考查了绝对值、列代数式,掌握绝对值越小越符合标准是解题的关键.
16.【答案】
【解析】解:,,
是等边三角形,
,,
,
,
,
在中,,
,
,
.
故答案为:.
依题意得是等边三角形,则,根据等腰三角形性质得,,则,进而得,然后再根据即可得出的长.
此题主要考查了等边三角形的性质,列代数式,等腰三角形的性质,熟练掌握等边三角形的性质,等腰三角形的性质是解决问题的关键.
17.【答案】解:设点表示的数为,根据题意得:
,
解得.
即点表示的数为.
故答案为:;
设点表示的数为,根据题意得:
,
解得或,
点到点的距离为或;
设点表示的数为,根据题意得:
,
解得或,
当时,
点到、两点的距离相等,
表示的数是,
点到点的距离为,
当时,
同理点到点的距离为,
点到点的距离是或.
【解析】设点表示的数为,根据点到点的距离是点到点距离的倍列出方程,求解即可;
设点表示的数为,根据点到点的距离为列出方程,求出,进而得到点到点的距离;
设点表示的数为,根据点到点的距离为,求出,进而得到点到点的距离.
本题考查一元一次方程的应用,数轴上的有理数,两点间的距离,解题的关键是用含字母的式子表示相关点表示的数及分类讨论思想的应用.
18.【答案】解:根据题意得:
故进货后这个商店有大米千克.
【解析】本题考查了整式的加减,解题的关键是根据题意列出算式,计算比较简单.
根据数量关系式计算,原来大米总重量上午卖出的重量下午购进的重量剩下的重量.
19.【答案】
【解析】解:对称到,对称到,
.
故答案为:,.
对称到,,得左边第个乘数为,
对称到,
.
故答案为:,.
中的对称到,得左边第个乘数为,
对称到,
.
故答案为:,.
.
证明:,
得证.
先找出数字对称的规律,以及数字之和的规律即可填空,再正确地列出等式证明即可.
本题主要考查学生寻找数字对称的规律,以及数字之和的规律的能力,正确地列出等式并证明是难点.
20.【答案】
【解析】解:,,,,
第行的第个数是,
故答案为:;
,,,,
第行的第个数是;
,,,,
第行的第个数是;
第行的第个数是,
第行的每一个数是第行的每一个数的,第行的每一个数是第行的每一个数的倍再加上,
若第行某列的数是,则第行该列的数是,第行该列的数是,
故答案为:,;
,,是每行的第个数,
,,,
.
根据,,,可以得出第行的第个数是,得到答案;
计算得出第行的第个数是,第行的第个数是,从而得出第行的每一个数是第行的每一个数的,第行的每一个数是第行的每一个数的倍再加上,由此即可得到答案;
先计算出、、的值,再代入进行计算即可得到答案.
本题考查数字的变化类规律探究、有理数的四则混合运算,根据题意得出第行的第个数是,第行的第个数是,第行的第个数是是解此题的关键.
21.【答案】
【解析】解:如图.
阴影部分的周长为.
故答案为:.
由图,得,.
图中阴影部分的面积为,
,
,
,
,
根据题意,得图中阴影部分的面积也是,
,
将、和代入,得,
将代入,得,
,
,
,
解得,
.
利用割补法计算即可;
根据图中、与和的数量关系作答即可;
图和中阴影部分的面积均为,据此得到、、、之间的数量关系,求出、,进而求出、,再由计算的长即可.
本题考查整式的混合运算、列代数式,根据几何图形长度之间的数量关系列代数式是解题的关键.
22.【答案】解:第二块实验田用水量表示为吨,第三块实验田用水量表示为吨;
已知第三块实验田用水量表示为:吨,
由题意列方程为:,
解得,
即第一块实验田用水量为吨,
则第二块实验田用水量为:,
第一块实验田和第二块实验田共用水: 吨,
答:另两块实验田共用水吨;
根据已知条件可列方程:,
解得:,
所以第一块实验田用水量为吨,
第二块实验田用水量为:吨,
第三块实验田用水量为:吨,
答:第一块实验田用水量为吨,第二块实验田用水量为吨,第三块实验田用水量为吨.
【解析】根据后两种方式用水量分别是漫灌的和,可分别求出另两块实验田的用水量;
根据第三块实验田用水吨,可以列方程,解出,再分别求另两块用水量,即可求出另两块实验田共用水量;
根据三块实验田的用水总量是第二块实验田和第三块实验田用水量的两倍还多吨,可列方程,解出,再分别求另两块用水量即可.
本题考查了一元一次方程的应用,列代数式,解题关键是弄清题意,找出等量关系,并根据等量关系列方程,再求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
