5.4一元一次方程的应用 人教版初中数学七年级上册同步练习(含详细答案解析)(含详细答案解析)
文档属性
| 名称 | 5.4一元一次方程的应用 人教版初中数学七年级上册同步练习(含详细答案解析)(含详细答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.4一元一次方程的应用人教版初中数学七年级上册同步练习(含详细答案解析)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
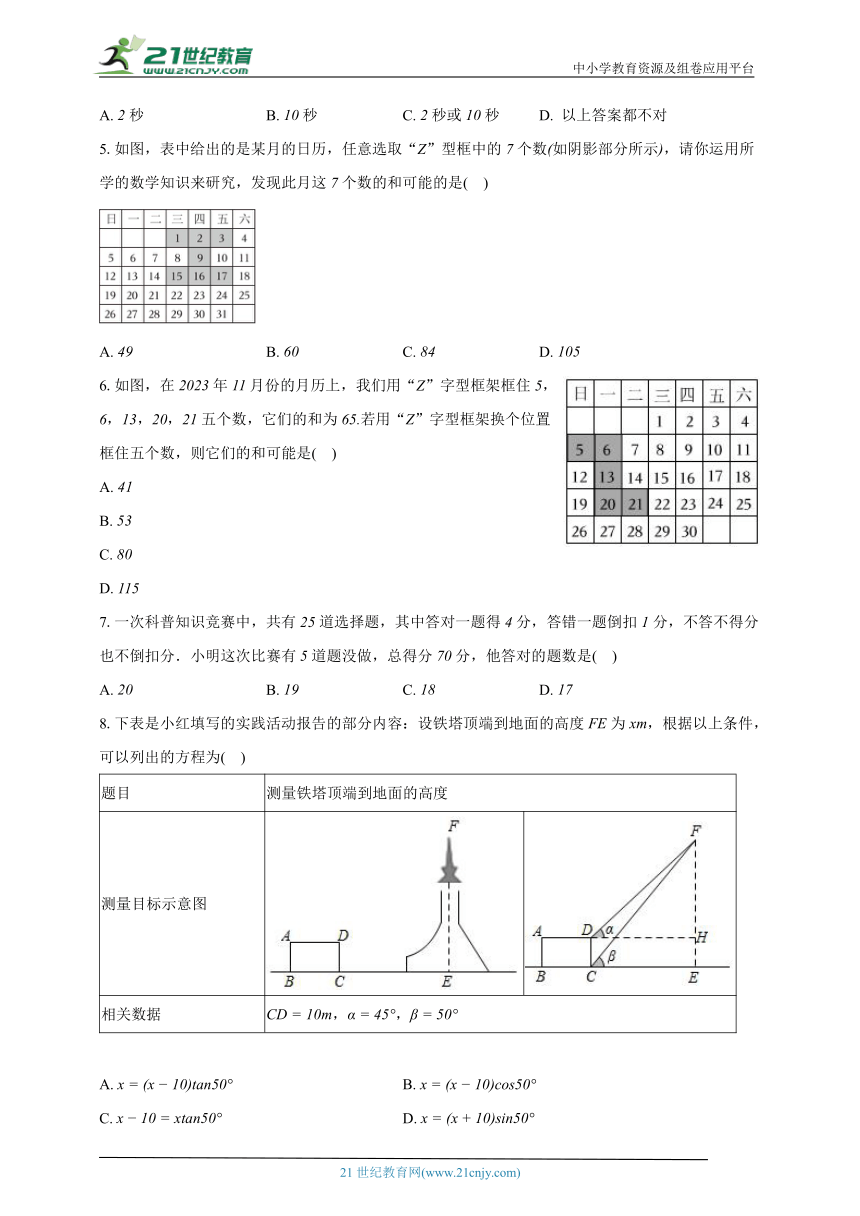
1.新年将至,如图是年月的日历,用笔在日历中任意框出两组呈斜对角线交叉的个代表日期的数,如图若设交叉框中的五个数分别为,,,,,且,则的值为( )
A. B. C. D.
2.如图,某校需要向某工厂定制一批四条腿的凳子,已知该工厂有名工人,每人每天可以生产块凳面或条凳腿,块凳面需要配条凳腿,为使每天生产的凳面和凳腿刚好配套,设安排名工人生产凳面,则下面所列方程正确的是( )
A. B.
C. D.
3.幻方,最早源于我国,古人称之为纵横图如图所示的幻方中,每一行、每一列及各条对角线上的三个数之和均相等,则的值为( )
A. B. C. D.
4.如图,已知,两点在数轴上,点表示的数为,,点以每秒个单位长度的速度从点向右运动.点以每秒个单位长度的速度从点向右运动点、点同时出发经过几秒,点、点分别到原点的距离相等?( )
A. 秒 B. 秒 C. 秒或秒 D. 以上答案都不对
5.如图,表中给出的是某月的日历,任意选取“”型框中的个数如阴影部分所示,请你运用所学的数学知识来研究,发现此月这个数的和可能的是( )
A. B. C. D.
6.如图,在年月份的月历上,我们用“”字型框架框住,,,,五个数,它们的和为若用“”字型框架换个位置框住五个数,则它们的和可能是( )
A.
B.
C.
D.
7.一次科普知识竞赛中,共有道选择题,其中答对一题得分,答错一题倒扣分,不答不得分也不倒扣分.小明这次比赛有道题没做,总得分分,他答对的题数是( )
A. B. C. D.
8.下表是小红填写的实践活动报告的部分内容:设铁塔顶端到地面的高度为,根据以上条件,可以列出的方程为( )
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据 ,,
A. B.
C. D.
9.已知某商店有两个进价不同的书包都卖了元,其中一个亏损,另一个盈利,在这次买卖中,这家商店( )
A. 盈利元 B. 盈利元 C. 亏损元 D. 不亏不赢
10.如图是年月的月历,用“”型框如阴影部分所示覆盖任意七个数并求它们的和,请你运用所学的知识,探索这七个数的和不可能的是( )
A. B. C. D.
11.如图,甲乙两只蚂蚁分别从数轴上的,两点处同时出发,相向而行甲蚂蚁的速度为每分钟个单位长度,乙蚂蚁的速度为每分钟个单位长度一只蝴蝶精灵与甲同时从地出发,当蝴蝶精灵碰到乙后,马上返回遇上甲,再返回遇上乙,依次反复,直至甲和乙两只蚂蚁相遇为止已知蝴蝶精灵的速度为每分钟个单位长度,那么,在这一过程中,蝴蝶精灵一共飞行了个单位长度.
A. B.
C. D. 缺少条件,无法计算
12.为了增强学生的安全防范意识,某校九班班委举行了一次安全知识抢答赛,共道题,记分规则如下:每答对一题得分,答错或不答倒扣分.小红共得了分,则小红答对题的道数为( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.在手工制作课上,老师组织七年级一班的学生用硬纸制作圆柱形茶叶筒七年级一班共有学生人,每名学生每小时剪筒身个或剪筒底个要求一个筒身配两个筒底,那么安排______人剪筒身,才能使每小时剪出的筒身与筒底配套.
14.某时装店将某品牌服装按成本提高标价,又以折优惠卖出,结果每件服装仍可获利元,则这种服装每件的成本价是______元
15.为了大力弘扬航天精神,科学普及航天知识,某校特意举行了“扬帆起航,逐梦九天”的知识竞赛.假设共道题,评分标准如下:答对题加分,答错题扣分,不答记分.已知小明不答的题比答错的题多道,他的总分为分,则小明答对了______道题.
16.一个书包的标价为元,按折出售仍可获利,该书包的进价为______元.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
甲容器中有浓度为的盐水克,乙容器中有克水把甲容器中盐水的一半倒入乙容器中;混合后,再把乙容器中现有盐水的一半倒入甲容器中;混合后,再把甲容器中的盐水倒入乙容器,使两个容器盐水一样多,问最后乙容器中的盐水浓度是多少?
18.本小题分
某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证元,仅限本人当年使用,凭证游泳每次再付费元;方式二:不购买会员证,每次游泳付费元设小明计划今年夏季游泳次数为为正整数.
根据题意,填写下表:
游泳次数
方式一的总费用元 ______ ______
方式二的总费用元 ______ ______
若小明计划今年夏季游泳的预算为元,选择哪种付费方式,他游泳的次数更多?
若小明用方式一付费比用方式二付费便宜元,则小明游泳了几次?
19.本小题分
定义:关于的方程与方程均为不等于的常数互为“反对方程”.
例如:方程与方程互为“反对方程”.
若方程与方程互为“反对方程”,则 ______;
若关于的方程与方程互为“反对方程”,求,的值.
20.本小题分
列方程解应用题:
我国元代数学家朱世杰所撰写的算学启蒙中有这样一道题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”
译文:良马平均每天能跑里,驽马平均每天能跑里.现驽马出发天后良马从同一地点出发沿同一路线追它,问良马多少天能够追上驽马?
21.本小题分
从广州到某市,可乘坐普通大巴走高速公路,也可以乘坐高铁.已知普通大巴行驶的路程是千米,高铁行驶的路程是普通大巴的倍.
求高铁行驶的路程;
若高铁行驶的平均速度千米时是普通大巴的平均速度千米时的倍,且乘坐高铁所需时间比普通大巴所需时间缩短小时,求高铁平均速度.
22.本小题分
某市居民生活用电峰谷电价如表:
高峰时间段用电价格表 低谷时间段用电价格表
高峰电价元千瓦时 低谷用电电量千瓦时 低谷电价元千瓦时
及以下部分
超过的部分
注:用电总量高峰用电量低谷用电量
小明家月份用电量中,高峰用电量为千瓦时,低谷用电量为千瓦时,这个月他家需付电费多少元?
小明家月份用电量中,高峰用电量为千瓦时,低谷用电量为千瓦时,请用含字母的整式表示他家月份需付的电费.
如果小明家月用电总量为千瓦时,需付电费元,那么这个月小明家高峰用电量和低谷用电量分别用了多少千瓦时?
答案和解析
1.【答案】
【解析】解:由图可得,,,
,
,
,
故选:.
由图形可得:,,代入即可得到关于的一元一次方程,解方程即可求解.
本题考查了一元一次方程的应用,根据图形得到,是解题的关键.
2.【答案】
【解析】解:设安排名工人生产凳面,则安排名工人生产凳腿,
依题意,得:.
故选:.
设安排名工人生产凳面,则安排名工人生产凳腿,根据生产的凳腿数量是凳面数量的倍,即可得出关于的一元一次方程,此题得解.
本题考查了由实际问题抽象出一元一次方程,理清题中的等量关系是解题的关键.
3.【答案】
【解析】解:如图,设左下角的方格中的数为.
每一行、每一列及各条对角线上的三个数之和均相等,
,
解得,
,
解得.
故选:.
设左下角的方格中的数为,根据题意列方程求出的值,然后根据题意列方程求出的值即可.
此题考查了一元一次方程的应用,解题的关键是根据等量关系列出方程.
4.【答案】
【解析】【分析】
此题主要考查了数轴,两点间的距离,一元一次方程的应用,解题关键是要读懂题目的意思.
根据题目给出的条件,找出合适的等量关系,列出方程,再求解.分点、点在点两侧;点、点重合两种情况讨论求解.
【解答】
解:点表示的数为,,
.
则对应的数是,
设经过秒,点、点分别到原点的距离相等,
点、点在点两侧,则,
解得;
点、点重合,则,
解得.
所以经过秒或秒,点、点分别到原点的距离相等。
故选:.
5.【答案】
【解析】【分析】
本题考查了一元一次方程的应用,正确表示出这个数的和是解答本题的关键.
先设中间的数为,则上一行个数分别是 , , ,下一行个数分别是 , , ,然后列方程求解即可.
【解答】
解:设中间的数为 ,则上一行个数分别是 , , ,下一行个数分别是 , , ,
则这个数的和为 ,
若 ,则 ,不符合题意;
B.若 ,则 ,不符合题意;
C.若 ,则 ,不符合题意;
D.若 ,则 ,符合题意;
故选:.
6.【答案】
【解析】解;设“”字型框架中最小的数为,则其他个数分别为,,,,
这五个数的和为,
当时,解得,不符合题意;
当时,解得,不符合题意;
当时,解得,,此时符合题意;
当时,解得,,此时不符合题意;
综上所述,这五个数的和可能为,
故选:.
设“”字型框架中最小的数为,则其他个数分别为,,,,然后求出这 五个数的和,进而建立方程求解即可.
本题主要考查了一元一次方程的应用,关键是根据题意找到等量关系式.
7.【答案】
【解析】【分析】
本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
根据题意可知:答对题目的得分答错题目的得分总得分,然后列出方程,再求解即可.
【解答】
解:设小明答对了道,则答错了道,
由题意可得:,
解得,
答:小明答对了道题目,
故答案为:
8.【答案】
【解析】解:过作于,
则四边形是矩形,
,,
,
,
,
,
,
,
故选:.
过作于,则四边形是矩形,根据矩形的性质得到,,求得,得到,根据三角函数的定义列方程即可得到结论.
本题考查了解直角三角形的应用,由实际问题抽象出一元一次方程,正确的识别图形是解题的关键.
9.【答案】
【解析】解:设盈利的进价为元,亏损的进价为元,由题意,得
,,
解得:,,
成本为:元.
售价为:元,
利润为:元.
故选:.
设盈利的进价为元,亏损的进价为元,根据销售问题的数量关系建立方程求出其解即可.
本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,销售问题的数量关系利润售价进价的运用,解答时由销售问题的数量关系建立方程是关键.
10.【答案】
【解析】【分析】
此题考查一元一次方程的实际运用,掌握“”型框中的个数的数字的排列规律是解决问题的关键.
设“”型框中的正中间的数为,则其他个数分别为,,,,,,表示出这个数之和,然后分别列出方程解答即可.
【解答】
解:设“”型框中的正中间的数为,则其他个数分别为,,,,,,
“”型框中的个数的和表示为:.
A.,解得,则,不能求出这个数,符合题意;
B.,解得,能求出这个数,不符合题意;
C.,解得,能求出这个数,不符合题意;
D.,解得,能求出这个数,不符合题意;
故选A.
11.【答案】
【解析】解:设甲乙两只蚂蚁经过分钟相遇,则蝴蝶精灵一共飞行了个单位,
根据题意可得,
,
解得,
.
蝴蝶精灵一共飞行了个单位长度.
故选:.
设甲乙两只蚂蚁经过分钟相遇,然后列方程求解即可.
此题考查了一元一次方程的应用,数轴,解题的关键是读懂题意,列方程求出甲乙两只蚂蚁相遇所用时间.
12.【答案】
【解析】解:设小红答对的个数为个,
由题意得,
解得,
故选:.
设小红答对的个数为个,根据抢答题一共个,记分规则如下:每答对一题得分,每答错或不答倒扣分,列出方程求解即可.
本题主要考查了一元一次方程的应用,正确理解题意是列出方程求解是解题的关键.
13.【答案】
【解析】解:设人剪筒身,则人剪筒底,
根据题意得,,
解得:,
人剪筒身,才能使每小时剪出的筒身与筒底配套,
故答案为:.
设人剪筒身,则人剪筒底,根据一个筒身配两个筒底列出方程,解方程即可得到答案.
本题考查了一元一次方程的应用,读懂题意,根据题中的等量关系,列出方程是解题的关键.
14.【答案】
【解析】解:设这种服装每件成本价为元,
,
解得:,
这种服装每件成本元,
故答案为:.
设这种服装每件成本价为元,根据“利润售价成本”,列出方程求解即可.
本题考查了一元一次方程的实际应用,关键是找到等量关系式.
15.【答案】
【解析】【分析】
本题主要考查一元一次方程的应用,解答的关键是理解清楚题意找到等量关系.
根据总分答对题数答错题数不答题数,设答错的题数为道,不答的题数为道,可列出方程,求出解.
【解答】
解:设答错的题数为道,不答的题数为道,依题意得:
,
解得:,
则不答的题数为:,
答对的题数为:道,
故答案为:.
16.【答案】
【解析】【分析】
本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.设该书包的进价为元,根据销售收入成本利润,即可得出关于的一元一次方程,解之即可得出结论.
【解答】
解:设该书包的进价为元,
根据题意得:,
解得:.
答:该书包的进价为元.
故答案为:.
17.【答案】解:乙容器中盐的质量:第一次混合后为克,第二次混合后为克,溶液总质量为:克,
甲容器中盐的质量:克,溶液总质量为:克,
最后使两个容器盐水一样多,
甲容器倒入乙容器的溶液质量为:克,
设最后乙容器中的盐水浓度是,
由题意得:,
解得:,
答:最后乙容器中的盐水浓度是.
【解析】先求出两次混合后甲、乙容器中盐的质量和溶液总质量,再设最后乙容器中的盐水浓度是,然后根据溶液浓度溶质,列出一元一次方程,解方程即可.
本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
18.【答案】
【解析】解:方式一:元,;
方式二:元,;
填表如图所示:
游泳次数
方式一的总费用元
方式二的总费用元
故答案为;;;.
由第问已知两种付费方式的总费用关于游泳次数的表达式,
令,解得,
即用方式一付费可以游泳次,
令,解得,
即用方式二付费可以游泳次,
答:选择方式一付费,他游泳的次数更多;
由第问已知两种付费方式的总费用关于游泳次数的表达式,
根据题意列方程为:
,
,
.
答:小明游泳了次.
根据两种付费分式计算、列式、填表即可;
根据中所得关系式,代入求出值,比较即可得答案;
根据方式一付费比用方式二付费便宜元列方程求解即可得解.
本题考查一元一次方程的应用以及列代数,明确题意,找出等量关系列方程是解题关键.
19.【答案】
【解析】解:若方程与方程互为“反对方程”,则,
故答案为:;
可变形为,
由题意知,,,
解得,.
根据互为“反对方程”的定义可得答案;
根据互为“反对方程”的定义列出关于和关于的一元一次方程,可得答案.
本题考查一元一次方程的应用,熟练掌握新定义运算,解一元一次方程的方法是解题的关键.
20.【答案】解:设良马天能够追上驽马.
根据题意得:,
解得:.
答:良马天能够追上驽马.
【解析】设良马天能够追上驽马,根据路程速度时间结合二者总路程相等,即可得出关于的一元一次方程,解之即可得出结论.
本题考查了一元一次方程的应用,根据路程速度时间结合二者总路程相等,列出关于的一元一次方程是解题的关键.
21.【答案】 千米;
高铁的平均速度是 千米时
【解析】【分析】高铁行驶的路程是普通大巴的 倍,普通大巴行驶的路程是 千米,两数相乘即可得出答案;
设普通大巴的平均速度是 千米时,则高铁平均速度是 千米时,列出分式方程,然后求解即可.
【详解】解:根据题意得: 千米,
答:高铁行驶的路程 千米;
设普通大巴的平均速度是 千米时,则高铁平均速度是 千米时,根据题意得:
.
解得 ,
经检验 是原方程的根,且符合题意,
所以高铁的平均速度是 千米时.
答:高铁的平均速度是 千米时.
【点睛】本题考查了分式方程的应用,关键是分析题意,找到合适的数量关系列出方程,解分式方程时要注意检验.
22.【答案】解:元,
答:他家需付电费元;
由于,需付的电费:
;
答:他家月份需付的电费为元;
当低谷用电量为千瓦时,需付电费为:
元元,
当总用电量一定时,低谷用电量越多,电费越小,
因此,低谷用电量超过千瓦时,
设低谷用电量为千瓦时,则高峰用电量为千瓦时,可列方程为:
,
解得,
所以这个月小明家低谷用电量为千瓦时,高峰用电量千瓦时.
【解析】根据“总电费高峰用电量的费用低谷用电量的费用”求解即可;
根据分段付费的方法进行计算电费即可;
首先判断低谷用电量超过千瓦时,然后再根据分段付费列方程求解即可.
本题主要考查列代数式、一元一次方程的应用,有理数的混合运算,关键是根据题意找到等量关系式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.4一元一次方程的应用人教版初中数学七年级上册同步练习(含详细答案解析)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.新年将至,如图是年月的日历,用笔在日历中任意框出两组呈斜对角线交叉的个代表日期的数,如图若设交叉框中的五个数分别为,,,,,且,则的值为( )
A. B. C. D.
2.如图,某校需要向某工厂定制一批四条腿的凳子,已知该工厂有名工人,每人每天可以生产块凳面或条凳腿,块凳面需要配条凳腿,为使每天生产的凳面和凳腿刚好配套,设安排名工人生产凳面,则下面所列方程正确的是( )
A. B.
C. D.
3.幻方,最早源于我国,古人称之为纵横图如图所示的幻方中,每一行、每一列及各条对角线上的三个数之和均相等,则的值为( )
A. B. C. D.
4.如图,已知,两点在数轴上,点表示的数为,,点以每秒个单位长度的速度从点向右运动.点以每秒个单位长度的速度从点向右运动点、点同时出发经过几秒,点、点分别到原点的距离相等?( )
A. 秒 B. 秒 C. 秒或秒 D. 以上答案都不对
5.如图,表中给出的是某月的日历,任意选取“”型框中的个数如阴影部分所示,请你运用所学的数学知识来研究,发现此月这个数的和可能的是( )
A. B. C. D.
6.如图,在年月份的月历上,我们用“”字型框架框住,,,,五个数,它们的和为若用“”字型框架换个位置框住五个数,则它们的和可能是( )
A.
B.
C.
D.
7.一次科普知识竞赛中,共有道选择题,其中答对一题得分,答错一题倒扣分,不答不得分也不倒扣分.小明这次比赛有道题没做,总得分分,他答对的题数是( )
A. B. C. D.
8.下表是小红填写的实践活动报告的部分内容:设铁塔顶端到地面的高度为,根据以上条件,可以列出的方程为( )
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据 ,,
A. B.
C. D.
9.已知某商店有两个进价不同的书包都卖了元,其中一个亏损,另一个盈利,在这次买卖中,这家商店( )
A. 盈利元 B. 盈利元 C. 亏损元 D. 不亏不赢
10.如图是年月的月历,用“”型框如阴影部分所示覆盖任意七个数并求它们的和,请你运用所学的知识,探索这七个数的和不可能的是( )
A. B. C. D.
11.如图,甲乙两只蚂蚁分别从数轴上的,两点处同时出发,相向而行甲蚂蚁的速度为每分钟个单位长度,乙蚂蚁的速度为每分钟个单位长度一只蝴蝶精灵与甲同时从地出发,当蝴蝶精灵碰到乙后,马上返回遇上甲,再返回遇上乙,依次反复,直至甲和乙两只蚂蚁相遇为止已知蝴蝶精灵的速度为每分钟个单位长度,那么,在这一过程中,蝴蝶精灵一共飞行了个单位长度.
A. B.
C. D. 缺少条件,无法计算
12.为了增强学生的安全防范意识,某校九班班委举行了一次安全知识抢答赛,共道题,记分规则如下:每答对一题得分,答错或不答倒扣分.小红共得了分,则小红答对题的道数为( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.在手工制作课上,老师组织七年级一班的学生用硬纸制作圆柱形茶叶筒七年级一班共有学生人,每名学生每小时剪筒身个或剪筒底个要求一个筒身配两个筒底,那么安排______人剪筒身,才能使每小时剪出的筒身与筒底配套.
14.某时装店将某品牌服装按成本提高标价,又以折优惠卖出,结果每件服装仍可获利元,则这种服装每件的成本价是______元
15.为了大力弘扬航天精神,科学普及航天知识,某校特意举行了“扬帆起航,逐梦九天”的知识竞赛.假设共道题,评分标准如下:答对题加分,答错题扣分,不答记分.已知小明不答的题比答错的题多道,他的总分为分,则小明答对了______道题.
16.一个书包的标价为元,按折出售仍可获利,该书包的进价为______元.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
甲容器中有浓度为的盐水克,乙容器中有克水把甲容器中盐水的一半倒入乙容器中;混合后,再把乙容器中现有盐水的一半倒入甲容器中;混合后,再把甲容器中的盐水倒入乙容器,使两个容器盐水一样多,问最后乙容器中的盐水浓度是多少?
18.本小题分
某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证元,仅限本人当年使用,凭证游泳每次再付费元;方式二:不购买会员证,每次游泳付费元设小明计划今年夏季游泳次数为为正整数.
根据题意,填写下表:
游泳次数
方式一的总费用元 ______ ______
方式二的总费用元 ______ ______
若小明计划今年夏季游泳的预算为元,选择哪种付费方式,他游泳的次数更多?
若小明用方式一付费比用方式二付费便宜元,则小明游泳了几次?
19.本小题分
定义:关于的方程与方程均为不等于的常数互为“反对方程”.
例如:方程与方程互为“反对方程”.
若方程与方程互为“反对方程”,则 ______;
若关于的方程与方程互为“反对方程”,求,的值.
20.本小题分
列方程解应用题:
我国元代数学家朱世杰所撰写的算学启蒙中有这样一道题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”
译文:良马平均每天能跑里,驽马平均每天能跑里.现驽马出发天后良马从同一地点出发沿同一路线追它,问良马多少天能够追上驽马?
21.本小题分
从广州到某市,可乘坐普通大巴走高速公路,也可以乘坐高铁.已知普通大巴行驶的路程是千米,高铁行驶的路程是普通大巴的倍.
求高铁行驶的路程;
若高铁行驶的平均速度千米时是普通大巴的平均速度千米时的倍,且乘坐高铁所需时间比普通大巴所需时间缩短小时,求高铁平均速度.
22.本小题分
某市居民生活用电峰谷电价如表:
高峰时间段用电价格表 低谷时间段用电价格表
高峰电价元千瓦时 低谷用电电量千瓦时 低谷电价元千瓦时
及以下部分
超过的部分
注:用电总量高峰用电量低谷用电量
小明家月份用电量中,高峰用电量为千瓦时,低谷用电量为千瓦时,这个月他家需付电费多少元?
小明家月份用电量中,高峰用电量为千瓦时,低谷用电量为千瓦时,请用含字母的整式表示他家月份需付的电费.
如果小明家月用电总量为千瓦时,需付电费元,那么这个月小明家高峰用电量和低谷用电量分别用了多少千瓦时?
答案和解析
1.【答案】
【解析】解:由图可得,,,
,
,
,
故选:.
由图形可得:,,代入即可得到关于的一元一次方程,解方程即可求解.
本题考查了一元一次方程的应用,根据图形得到,是解题的关键.
2.【答案】
【解析】解:设安排名工人生产凳面,则安排名工人生产凳腿,
依题意,得:.
故选:.
设安排名工人生产凳面,则安排名工人生产凳腿,根据生产的凳腿数量是凳面数量的倍,即可得出关于的一元一次方程,此题得解.
本题考查了由实际问题抽象出一元一次方程,理清题中的等量关系是解题的关键.
3.【答案】
【解析】解:如图,设左下角的方格中的数为.
每一行、每一列及各条对角线上的三个数之和均相等,
,
解得,
,
解得.
故选:.
设左下角的方格中的数为,根据题意列方程求出的值,然后根据题意列方程求出的值即可.
此题考查了一元一次方程的应用,解题的关键是根据等量关系列出方程.
4.【答案】
【解析】【分析】
此题主要考查了数轴,两点间的距离,一元一次方程的应用,解题关键是要读懂题目的意思.
根据题目给出的条件,找出合适的等量关系,列出方程,再求解.分点、点在点两侧;点、点重合两种情况讨论求解.
【解答】
解:点表示的数为,,
.
则对应的数是,
设经过秒,点、点分别到原点的距离相等,
点、点在点两侧,则,
解得;
点、点重合,则,
解得.
所以经过秒或秒,点、点分别到原点的距离相等。
故选:.
5.【答案】
【解析】【分析】
本题考查了一元一次方程的应用,正确表示出这个数的和是解答本题的关键.
先设中间的数为,则上一行个数分别是 , , ,下一行个数分别是 , , ,然后列方程求解即可.
【解答】
解:设中间的数为 ,则上一行个数分别是 , , ,下一行个数分别是 , , ,
则这个数的和为 ,
若 ,则 ,不符合题意;
B.若 ,则 ,不符合题意;
C.若 ,则 ,不符合题意;
D.若 ,则 ,符合题意;
故选:.
6.【答案】
【解析】解;设“”字型框架中最小的数为,则其他个数分别为,,,,
这五个数的和为,
当时,解得,不符合题意;
当时,解得,不符合题意;
当时,解得,,此时符合题意;
当时,解得,,此时不符合题意;
综上所述,这五个数的和可能为,
故选:.
设“”字型框架中最小的数为,则其他个数分别为,,,,然后求出这 五个数的和,进而建立方程求解即可.
本题主要考查了一元一次方程的应用,关键是根据题意找到等量关系式.
7.【答案】
【解析】【分析】
本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
根据题意可知:答对题目的得分答错题目的得分总得分,然后列出方程,再求解即可.
【解答】
解:设小明答对了道,则答错了道,
由题意可得:,
解得,
答:小明答对了道题目,
故答案为:
8.【答案】
【解析】解:过作于,
则四边形是矩形,
,,
,
,
,
,
,
,
故选:.
过作于,则四边形是矩形,根据矩形的性质得到,,求得,得到,根据三角函数的定义列方程即可得到结论.
本题考查了解直角三角形的应用,由实际问题抽象出一元一次方程,正确的识别图形是解题的关键.
9.【答案】
【解析】解:设盈利的进价为元,亏损的进价为元,由题意,得
,,
解得:,,
成本为:元.
售价为:元,
利润为:元.
故选:.
设盈利的进价为元,亏损的进价为元,根据销售问题的数量关系建立方程求出其解即可.
本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,销售问题的数量关系利润售价进价的运用,解答时由销售问题的数量关系建立方程是关键.
10.【答案】
【解析】【分析】
此题考查一元一次方程的实际运用,掌握“”型框中的个数的数字的排列规律是解决问题的关键.
设“”型框中的正中间的数为,则其他个数分别为,,,,,,表示出这个数之和,然后分别列出方程解答即可.
【解答】
解:设“”型框中的正中间的数为,则其他个数分别为,,,,,,
“”型框中的个数的和表示为:.
A.,解得,则,不能求出这个数,符合题意;
B.,解得,能求出这个数,不符合题意;
C.,解得,能求出这个数,不符合题意;
D.,解得,能求出这个数,不符合题意;
故选A.
11.【答案】
【解析】解:设甲乙两只蚂蚁经过分钟相遇,则蝴蝶精灵一共飞行了个单位,
根据题意可得,
,
解得,
.
蝴蝶精灵一共飞行了个单位长度.
故选:.
设甲乙两只蚂蚁经过分钟相遇,然后列方程求解即可.
此题考查了一元一次方程的应用,数轴,解题的关键是读懂题意,列方程求出甲乙两只蚂蚁相遇所用时间.
12.【答案】
【解析】解:设小红答对的个数为个,
由题意得,
解得,
故选:.
设小红答对的个数为个,根据抢答题一共个,记分规则如下:每答对一题得分,每答错或不答倒扣分,列出方程求解即可.
本题主要考查了一元一次方程的应用,正确理解题意是列出方程求解是解题的关键.
13.【答案】
【解析】解:设人剪筒身,则人剪筒底,
根据题意得,,
解得:,
人剪筒身,才能使每小时剪出的筒身与筒底配套,
故答案为:.
设人剪筒身,则人剪筒底,根据一个筒身配两个筒底列出方程,解方程即可得到答案.
本题考查了一元一次方程的应用,读懂题意,根据题中的等量关系,列出方程是解题的关键.
14.【答案】
【解析】解:设这种服装每件成本价为元,
,
解得:,
这种服装每件成本元,
故答案为:.
设这种服装每件成本价为元,根据“利润售价成本”,列出方程求解即可.
本题考查了一元一次方程的实际应用,关键是找到等量关系式.
15.【答案】
【解析】【分析】
本题主要考查一元一次方程的应用,解答的关键是理解清楚题意找到等量关系.
根据总分答对题数答错题数不答题数,设答错的题数为道,不答的题数为道,可列出方程,求出解.
【解答】
解:设答错的题数为道,不答的题数为道,依题意得:
,
解得:,
则不答的题数为:,
答对的题数为:道,
故答案为:.
16.【答案】
【解析】【分析】
本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.设该书包的进价为元,根据销售收入成本利润,即可得出关于的一元一次方程,解之即可得出结论.
【解答】
解:设该书包的进价为元,
根据题意得:,
解得:.
答:该书包的进价为元.
故答案为:.
17.【答案】解:乙容器中盐的质量:第一次混合后为克,第二次混合后为克,溶液总质量为:克,
甲容器中盐的质量:克,溶液总质量为:克,
最后使两个容器盐水一样多,
甲容器倒入乙容器的溶液质量为:克,
设最后乙容器中的盐水浓度是,
由题意得:,
解得:,
答:最后乙容器中的盐水浓度是.
【解析】先求出两次混合后甲、乙容器中盐的质量和溶液总质量,再设最后乙容器中的盐水浓度是,然后根据溶液浓度溶质,列出一元一次方程,解方程即可.
本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
18.【答案】
【解析】解:方式一:元,;
方式二:元,;
填表如图所示:
游泳次数
方式一的总费用元
方式二的总费用元
故答案为;;;.
由第问已知两种付费方式的总费用关于游泳次数的表达式,
令,解得,
即用方式一付费可以游泳次,
令,解得,
即用方式二付费可以游泳次,
答:选择方式一付费,他游泳的次数更多;
由第问已知两种付费方式的总费用关于游泳次数的表达式,
根据题意列方程为:
,
,
.
答:小明游泳了次.
根据两种付费分式计算、列式、填表即可;
根据中所得关系式,代入求出值,比较即可得答案;
根据方式一付费比用方式二付费便宜元列方程求解即可得解.
本题考查一元一次方程的应用以及列代数,明确题意,找出等量关系列方程是解题关键.
19.【答案】
【解析】解:若方程与方程互为“反对方程”,则,
故答案为:;
可变形为,
由题意知,,,
解得,.
根据互为“反对方程”的定义可得答案;
根据互为“反对方程”的定义列出关于和关于的一元一次方程,可得答案.
本题考查一元一次方程的应用,熟练掌握新定义运算,解一元一次方程的方法是解题的关键.
20.【答案】解:设良马天能够追上驽马.
根据题意得:,
解得:.
答:良马天能够追上驽马.
【解析】设良马天能够追上驽马,根据路程速度时间结合二者总路程相等,即可得出关于的一元一次方程,解之即可得出结论.
本题考查了一元一次方程的应用,根据路程速度时间结合二者总路程相等,列出关于的一元一次方程是解题的关键.
21.【答案】 千米;
高铁的平均速度是 千米时
【解析】【分析】高铁行驶的路程是普通大巴的 倍,普通大巴行驶的路程是 千米,两数相乘即可得出答案;
设普通大巴的平均速度是 千米时,则高铁平均速度是 千米时,列出分式方程,然后求解即可.
【详解】解:根据题意得: 千米,
答:高铁行驶的路程 千米;
设普通大巴的平均速度是 千米时,则高铁平均速度是 千米时,根据题意得:
.
解得 ,
经检验 是原方程的根,且符合题意,
所以高铁的平均速度是 千米时.
答:高铁的平均速度是 千米时.
【点睛】本题考查了分式方程的应用,关键是分析题意,找到合适的数量关系列出方程,解分式方程时要注意检验.
22.【答案】解:元,
答:他家需付电费元;
由于,需付的电费:
;
答:他家月份需付的电费为元;
当低谷用电量为千瓦时,需付电费为:
元元,
当总用电量一定时,低谷用电量越多,电费越小,
因此,低谷用电量超过千瓦时,
设低谷用电量为千瓦时,则高峰用电量为千瓦时,可列方程为:
,
解得,
所以这个月小明家低谷用电量为千瓦时,高峰用电量千瓦时.
【解析】根据“总电费高峰用电量的费用低谷用电量的费用”求解即可;
根据分段付费的方法进行计算电费即可;
首先判断低谷用电量超过千瓦时,然后再根据分段付费列方程求解即可.
本题主要考查列代数式、一元一次方程的应用,有理数的混合运算,关键是根据题意找到等量关系式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
