8.1 习题课:变力做功的计算(共16张PPT)
文档属性
| 名称 | 8.1 习题课:变力做功的计算(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-25 19:22:46 | ||
图片预览





文档简介
(共16张PPT)
专题:变力做功的计算
第八章 机械能守恒定律
人教版(2019)必修 第二册
知道变力做功的解题常见思路和方法
拓展解题思路,提高分析问题的能力
学习目标
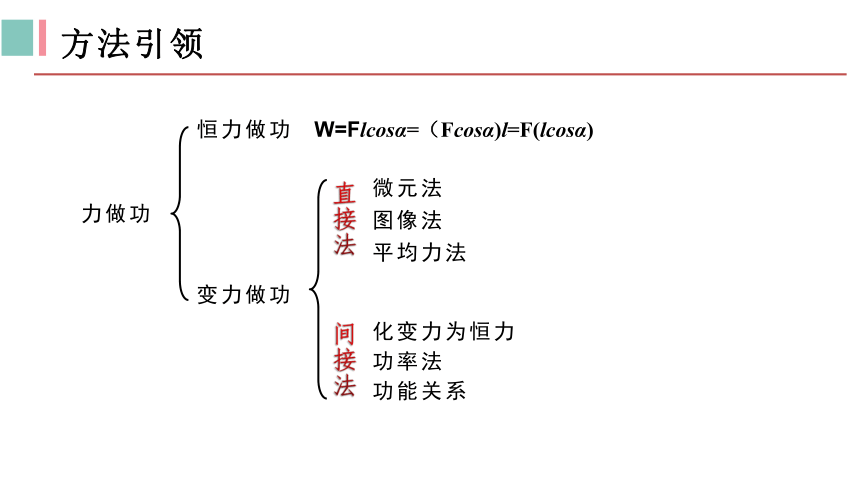
力做功
恒力做功
变力做功
W=Flcosα=(Fcosα)l=F(lcosα)
微元法
图像法
平均力法
功能关系
功率法
化变力为恒力
方法引领
直接法
间接法
例1 如图所示,在西部的偏远山区,人们至今还通过“驴拉磨”的方式把小麦颗粒加工成粗面来食用。假设驴拉磨的平均拉力大小为300 N,驴做圆周运动的等效半径r=1.5m,则驴拉磨转动一周所做的功约为( )
A.0 B.300J C.1400J D.2800J
1.微元法(拉磨模型)
一、直接法
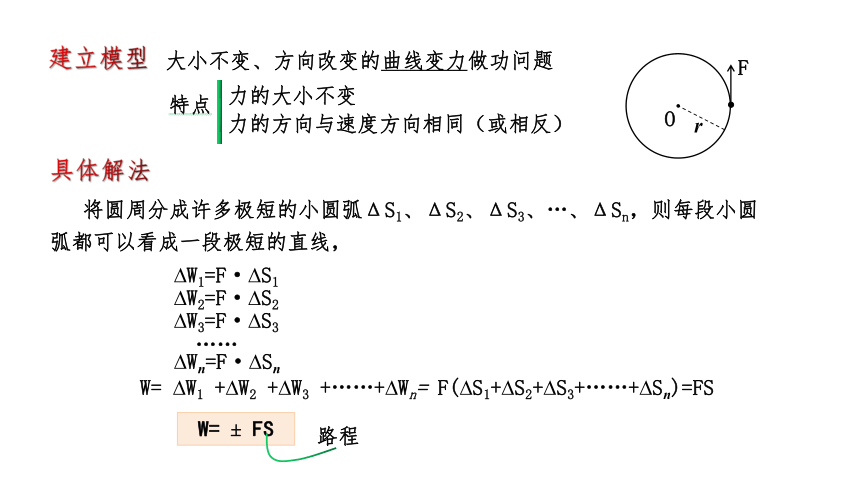
建立模型
特点
将圆周分成许多极短的小圆弧ΔS1、ΔS2、ΔS3、…、ΔSn,则每段小圆弧都可以看成一段极短的直线,
具体解法
W1=F· S1
W2=F· S2
W3=F· S3
……
Wn=F· Sn
W= W1 + W2 + W3 +……+ Wn= F( S1+ S2+ S3+……+ Sn)=FS
W= FS
+
-
路程
F
r
O
大小不变、方向改变的曲线变力做功问题
力的方向与速度方向相同(或相反)
力的大小不变
例1 如图所示,在西部的偏远山区,人们至今还通过“驴拉磨”的方式把小麦颗粒加工成粗面来食用。假设驴拉磨的平均拉力大小为300 N,驴做圆周运动的等效半径r=1.5m,则驴拉磨转动一周所做的功约为( )
A.0 B.300J C.1400J D.2800J
【参考答案】D
2.图像法
当力与位移同向共线时:
可将变力做功的F-x图像画出,图线与坐标轴所围“面积”的代数和就表示力F在这段位移内做的功。
F
l
F
l
O
F
l
恒力情况
启示:利用F x图像求变力做功
F
原长态
伸长态
l
WF= Fl = kl2
F
l
O
F
l
l
O
F
l
⑴缓慢拉伸轻弹簧
⑵一般情况
3.平均力法
适用条件
F
l
O
F
l
⑴ 力F的方向一定
⑵ F—l 线性变化
l :力作用点的位移
木块缓慢移动的过程,拉力做的功W2=Fx2=40×0.4 J=16 J。故拉力所做的总功W=W1+W2=20 J.
【解析1】 木块刚要滑动时,拉力的大小F=kx1=200×0.2 N=40 N,从开始到木块刚要滑动的过程,拉力做的功
【答案】20 J
例2 如图,放在水平地面上的木块与一劲度系数k=200 N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2 m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4 m,求上述过程中拉力所做的功。
【解析2】 画出F-x图象,图像与横坐标所围成的面积表示拉力的功,则有
1.变力转换恒力法(简称为“转换法”或“等效法”)——区别平均值类型
若某一变力做功和某一恒力做功相等,则可以用求得的恒力的功来作为变力的功。
关键点:
利用功的定义式W=Flcosα求恒力的功。
二、间接法
分析清楚该变力做功到底与哪个恒力做功是相同的。
思想:
计算方法:
例3 如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功。
【分析】 轻绳不存储能量,恒力F做功通过绳子将能量转移到物体上,故此恒力F做功应该等于绳子对物体做的功。
h
A
B
F
练习 如图所示,一辆拖车通过光滑定滑轮拉动一重物G匀速提升,当拖车从A点水平移动到B点时,位移为S,绳子由竖直变为与竖直方向成θ角度,求此过程中拖车对绳子所做的功。
【解析】 拖车对绳子做的功等于绳子对重物做的功。以重物为研究对象,由于整个过程中重物匀速运动,
所以绳子的拉力大小
重物上升的距离
所以绳子对重物做功
拖车对绳子做功等于绳子对重物做功,为
若变力做功的功率恒定,且做功时间已知的,则有
3.功能关系法(重点)
2.功率法
W=Pt
力做功
恒力做功
变力做功
W=Flcosα =(Fcosα)l=F(lcosα)
直接法
间接法
微元法
图像法
平均力法
功能关系
功率法
化变力为恒力
课堂小结
专题:变力做功的计算
第八章 机械能守恒定律
人教版(2019)必修 第二册
知道变力做功的解题常见思路和方法
拓展解题思路,提高分析问题的能力
学习目标
力做功
恒力做功
变力做功
W=Flcosα=(Fcosα)l=F(lcosα)
微元法
图像法
平均力法
功能关系
功率法
化变力为恒力
方法引领
直接法
间接法
例1 如图所示,在西部的偏远山区,人们至今还通过“驴拉磨”的方式把小麦颗粒加工成粗面来食用。假设驴拉磨的平均拉力大小为300 N,驴做圆周运动的等效半径r=1.5m,则驴拉磨转动一周所做的功约为( )
A.0 B.300J C.1400J D.2800J
1.微元法(拉磨模型)
一、直接法
建立模型
特点
将圆周分成许多极短的小圆弧ΔS1、ΔS2、ΔS3、…、ΔSn,则每段小圆弧都可以看成一段极短的直线,
具体解法
W1=F· S1
W2=F· S2
W3=F· S3
……
Wn=F· Sn
W= W1 + W2 + W3 +……+ Wn= F( S1+ S2+ S3+……+ Sn)=FS
W= FS
+
-
路程
F
r
O
大小不变、方向改变的曲线变力做功问题
力的方向与速度方向相同(或相反)
力的大小不变
例1 如图所示,在西部的偏远山区,人们至今还通过“驴拉磨”的方式把小麦颗粒加工成粗面来食用。假设驴拉磨的平均拉力大小为300 N,驴做圆周运动的等效半径r=1.5m,则驴拉磨转动一周所做的功约为( )
A.0 B.300J C.1400J D.2800J
【参考答案】D
2.图像法
当力与位移同向共线时:
可将变力做功的F-x图像画出,图线与坐标轴所围“面积”的代数和就表示力F在这段位移内做的功。
F
l
F
l
O
F
l
恒力情况
启示:利用F x图像求变力做功
F
原长态
伸长态
l
WF= Fl = kl2
F
l
O
F
l
l
O
F
l
⑴缓慢拉伸轻弹簧
⑵一般情况
3.平均力法
适用条件
F
l
O
F
l
⑴ 力F的方向一定
⑵ F—l 线性变化
l :力作用点的位移
木块缓慢移动的过程,拉力做的功W2=Fx2=40×0.4 J=16 J。故拉力所做的总功W=W1+W2=20 J.
【解析1】 木块刚要滑动时,拉力的大小F=kx1=200×0.2 N=40 N,从开始到木块刚要滑动的过程,拉力做的功
【答案】20 J
例2 如图,放在水平地面上的木块与一劲度系数k=200 N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2 m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4 m,求上述过程中拉力所做的功。
【解析2】 画出F-x图象,图像与横坐标所围成的面积表示拉力的功,则有
1.变力转换恒力法(简称为“转换法”或“等效法”)——区别平均值类型
若某一变力做功和某一恒力做功相等,则可以用求得的恒力的功来作为变力的功。
关键点:
利用功的定义式W=Flcosα求恒力的功。
二、间接法
分析清楚该变力做功到底与哪个恒力做功是相同的。
思想:
计算方法:
例3 如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功。
【分析】 轻绳不存储能量,恒力F做功通过绳子将能量转移到物体上,故此恒力F做功应该等于绳子对物体做的功。
h
A
B
F
练习 如图所示,一辆拖车通过光滑定滑轮拉动一重物G匀速提升,当拖车从A点水平移动到B点时,位移为S,绳子由竖直变为与竖直方向成θ角度,求此过程中拖车对绳子所做的功。
【解析】 拖车对绳子做的功等于绳子对重物做的功。以重物为研究对象,由于整个过程中重物匀速运动,
所以绳子的拉力大小
重物上升的距离
所以绳子对重物做功
拖车对绳子做功等于绳子对重物做功,为
若变力做功的功率恒定,且做功时间已知的,则有
3.功能关系法(重点)
2.功率法
W=Pt
力做功
恒力做功
变力做功
W=Flcosα =(Fcosα)l=F(lcosα)
直接法
间接法
微元法
图像法
平均力法
功能关系
功率法
化变力为恒力
课堂小结
