第五周—九年级上册数学人教版(2012)每周测验 考查范围:22.2-22.3 (含解析)
文档属性
| 名称 | 第五周—九年级上册数学人教版(2012)每周测验 考查范围:22.2-22.3 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 519.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 22:46:07 | ||
图片预览

文档简介
第五周—九年级上册数学人教版(2012)每周测验
考查范围:22.2-22.3
1.小康在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离,则小康此次掷球的成绩(即的长度)是( )
A. B. C. D.
2.已知二次函数(a,b,c是常数,),当时,,若此一元二次方程有两个不相等的实数根,则该二次函数的图象可能是( )
A. B. C. D.
3.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是,则所获利润最多为( )
A.15元 B.400元 C.800元 D.1250元
4.已知二次函数的图象在x轴的下方,则a,b,c满足的条件是( )
A., B.,
C., D.,
5.用一段长度为的篱笆围成一个矩形菜地,能围成菜地的面积不可能是( ).
A. B. C. D.
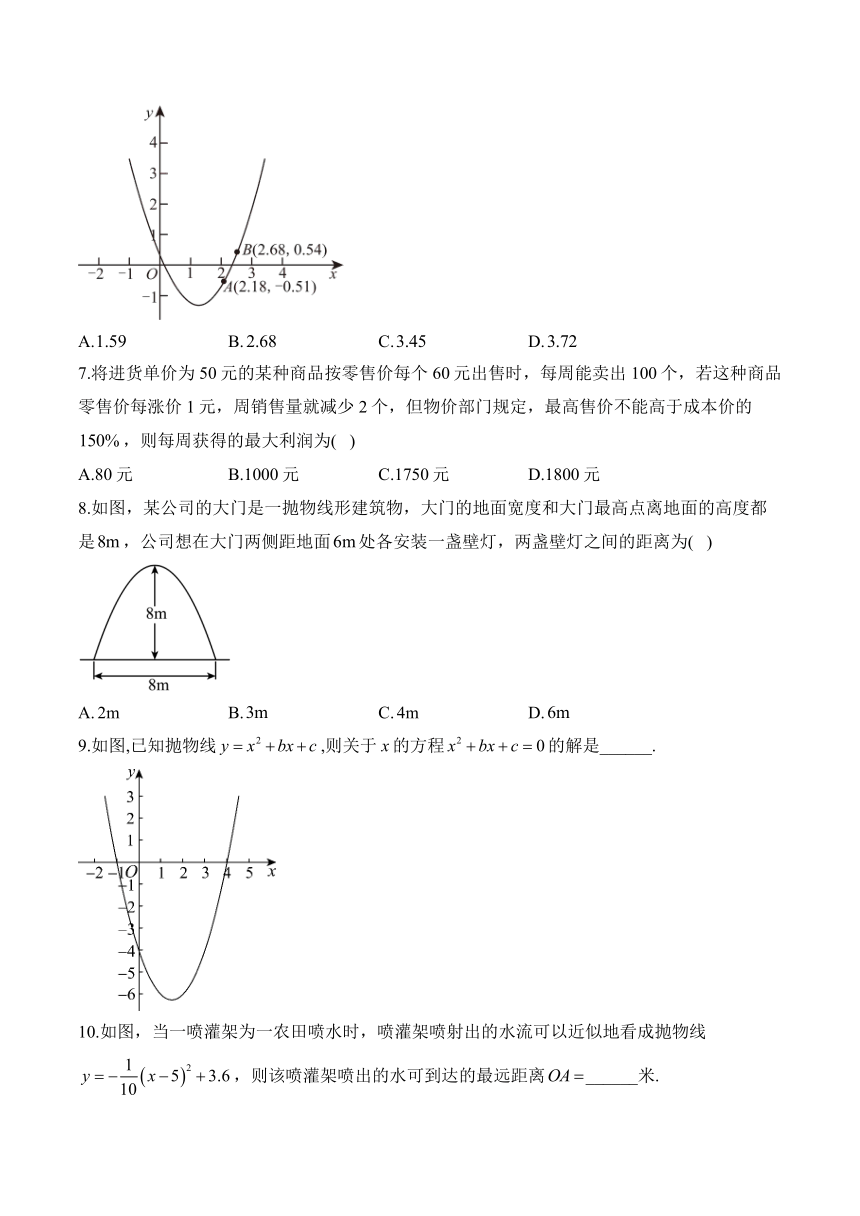
6.如图是二次函数的图象,图象上有两点分别为,,则方程的一个解只可能是( )
A. B. C. D.
7.将进货单价为50元的某种商品按零售价每个60元出售时,每周能卖出100个,若这种商品零售价每涨价1元,周销售量就减少2个,但物价部门规定,最高售价不能高于成本价的,则每周获得的最大利润为( )
A.80元 B.1000元 C.1750元 D.1800元
8.如图,某公司的大门是一抛物线形建筑物,大门的地面宽度和大门最高点离地面的高度都是,公司想在大门两侧距地面处各安装一盏壁灯,两盏壁灯之间的距离为( )
A. B. C. D.
9.如图,已知抛物线,则关于x的方程的解是______.
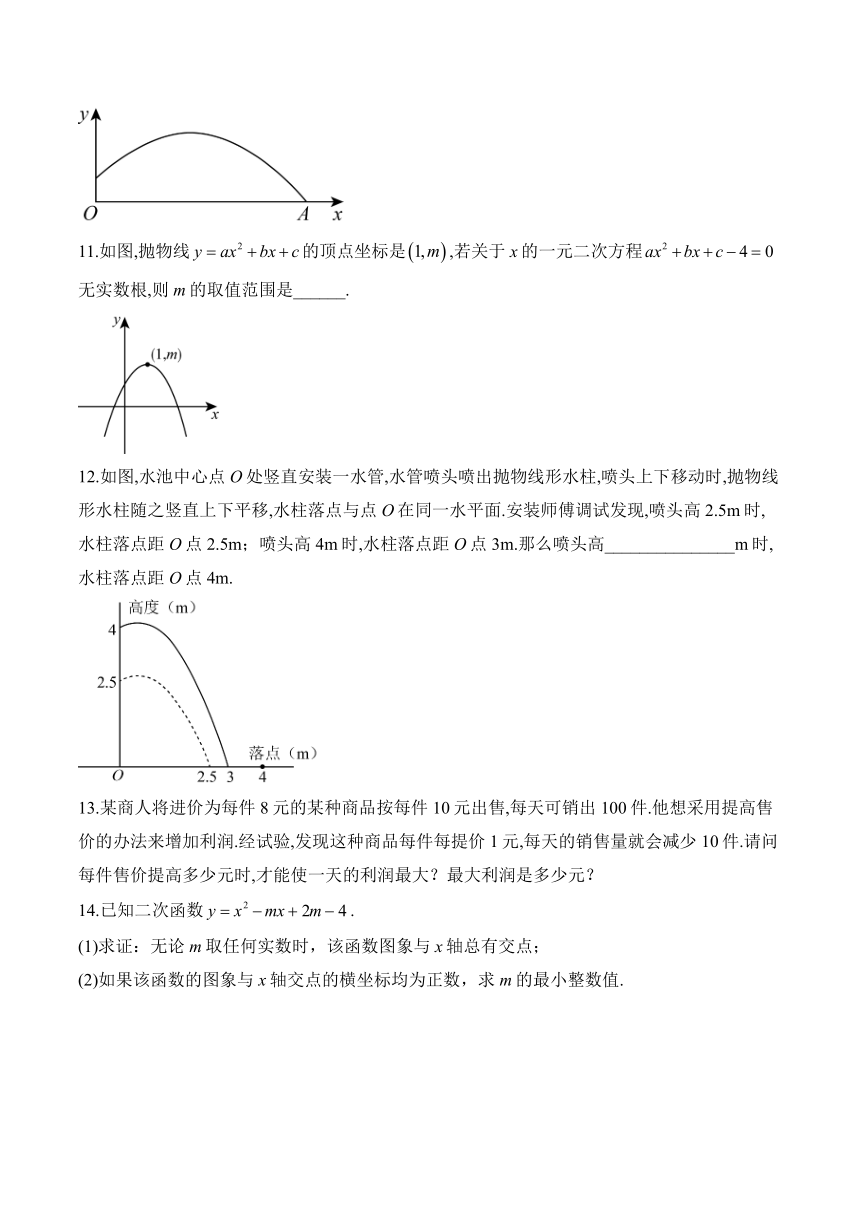
10.如图,当一喷灌架为一农田喷水时,喷灌架喷射出的水流可以近似地看成抛物线,则该喷灌架喷出的水可到达的最远距离______米.
11.如图,抛物线的顶点坐标是,若关于x的一元二次方程无实数根,则m的取值范围是______.
12.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高2.5m时,水柱落点距O点2.5m;喷头高4m时,水柱落点距O点3m.那么喷头高_______________m时,水柱落点距O点4m.
13.某商人将进价为每件8元的某种商品按每件10元出售,每天可销出100件.他想采用提高售价的办法来增加利润.经试验,发现这种商品每件每提价1元,每天的销售量就会减少10件.请问每件售价提高多少元时,才能使一天的利润最大?最大利润是多少元?
14.已知二次函数.
(1)求证:无论m取任何实数时,该函数图象与x轴总有交点;
(2)如果该函数的图象与x轴交点的横坐标均为正数,求m的最小整数值.
答案以及解析
1.答案:B
解析:令,则,
解得:,(舍去)
故选B.
2.答案:C
解析:当时,有两个不相等的实根,
∴,即二次函数图象与x轴有两个交点,
∴根据图示可得,
A、与x轴无交点,不符合题意;
B、与x轴有一个交代,不符合题意;
C、与x轴有两个交点,符合题意;
D、与x轴有一个交代,不符合题意;
故选:C.
3.答案:D
解析:,
因为,所以当时,y有最大值,最大值为1250,即所获利润最多为1250元.
4.答案:C
解析:二次函教的图象在x轴的下方,
抛物线开口向下,与x轴无交点,
即,,
故选:C.
5.答案:D
解析:设菜地的长为,面积为,则宽为,,
依题意得,,
,
当时,面积最大,最大值为,
,
能围成菜地的面积不可能是,
故选:D.
6.答案:C
解析:二次函数图象上有两点分别为,,
方程的一个解,
方程的解为:,
即.
故选:C.
7.答案:C
解析:设涨价x元,每周获利,
最高售价不能高于成本价的,
,
,
,
当时,y随x的增大而增大,
故当时,y的最大值为,
故应选:C.
8.答案:C
解析:建立如图所示坐标系,抛物线的顶点坐标为,
设抛物线解析式为
抛物线过,
把代入
,
两壁灯之间的水平距离为,
故选:C.
9.答案:
解析:由函数图象可知抛物线与x轴交于,,
∴关于x的方程的解是,,
故答案为:,.
10.答案:11
解析:对于,令,则,
解得:,(舍),
,
米.
故答案为:11.
11.答案:
解析:∵关于x的一元二次方程无实数根,
∴抛物线与没有交点,
∵抛物线的顶点坐标是,
∴.
故答案为:.
12.答案:8
解析:由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,
当喷头高2.5m时,可设,
将代入解析式得出①,
喷头高4m时,可设,
将(3,0)代入解析式得②,
联立可求出,,
设喷头高为h时,水柱落点距O点4m,
∴此时的解析式为,
将代入可得,
解得.
故答案为:8.
13.答案:每件售价提高4元时,才能使一天的利润最大,最大利润是360元
解析:设每件售价提高x元,每天的利润为y元,则每件的利润为元,每天的销售量为件,
∴,解得:.
依题意有:.
∵,∴当时,y最大,最大值为360,
∴每件售价提高4元时,才能使一天的利润最大,最大利润是360元.
14.答案:(1)见解析
(2)
解析:(1)由题意,得,
无论m取任何实数时,该函数图象与x轴总有交点.
(2),,.
该函数的图象与x轴交点的横坐标均为正数,
,即.
m取最小整数;.
考查范围:22.2-22.3
1.小康在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离,则小康此次掷球的成绩(即的长度)是( )
A. B. C. D.
2.已知二次函数(a,b,c是常数,),当时,,若此一元二次方程有两个不相等的实数根,则该二次函数的图象可能是( )
A. B. C. D.
3.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是,则所获利润最多为( )
A.15元 B.400元 C.800元 D.1250元
4.已知二次函数的图象在x轴的下方,则a,b,c满足的条件是( )
A., B.,
C., D.,
5.用一段长度为的篱笆围成一个矩形菜地,能围成菜地的面积不可能是( ).
A. B. C. D.
6.如图是二次函数的图象,图象上有两点分别为,,则方程的一个解只可能是( )
A. B. C. D.
7.将进货单价为50元的某种商品按零售价每个60元出售时,每周能卖出100个,若这种商品零售价每涨价1元,周销售量就减少2个,但物价部门规定,最高售价不能高于成本价的,则每周获得的最大利润为( )
A.80元 B.1000元 C.1750元 D.1800元
8.如图,某公司的大门是一抛物线形建筑物,大门的地面宽度和大门最高点离地面的高度都是,公司想在大门两侧距地面处各安装一盏壁灯,两盏壁灯之间的距离为( )
A. B. C. D.
9.如图,已知抛物线,则关于x的方程的解是______.
10.如图,当一喷灌架为一农田喷水时,喷灌架喷射出的水流可以近似地看成抛物线,则该喷灌架喷出的水可到达的最远距离______米.
11.如图,抛物线的顶点坐标是,若关于x的一元二次方程无实数根,则m的取值范围是______.
12.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高2.5m时,水柱落点距O点2.5m;喷头高4m时,水柱落点距O点3m.那么喷头高_______________m时,水柱落点距O点4m.
13.某商人将进价为每件8元的某种商品按每件10元出售,每天可销出100件.他想采用提高售价的办法来增加利润.经试验,发现这种商品每件每提价1元,每天的销售量就会减少10件.请问每件售价提高多少元时,才能使一天的利润最大?最大利润是多少元?
14.已知二次函数.
(1)求证:无论m取任何实数时,该函数图象与x轴总有交点;
(2)如果该函数的图象与x轴交点的横坐标均为正数,求m的最小整数值.
答案以及解析
1.答案:B
解析:令,则,
解得:,(舍去)
故选B.
2.答案:C
解析:当时,有两个不相等的实根,
∴,即二次函数图象与x轴有两个交点,
∴根据图示可得,
A、与x轴无交点,不符合题意;
B、与x轴有一个交代,不符合题意;
C、与x轴有两个交点,符合题意;
D、与x轴有一个交代,不符合题意;
故选:C.
3.答案:D
解析:,
因为,所以当时,y有最大值,最大值为1250,即所获利润最多为1250元.
4.答案:C
解析:二次函教的图象在x轴的下方,
抛物线开口向下,与x轴无交点,
即,,
故选:C.
5.答案:D
解析:设菜地的长为,面积为,则宽为,,
依题意得,,
,
当时,面积最大,最大值为,
,
能围成菜地的面积不可能是,
故选:D.
6.答案:C
解析:二次函数图象上有两点分别为,,
方程的一个解,
方程的解为:,
即.
故选:C.
7.答案:C
解析:设涨价x元,每周获利,
最高售价不能高于成本价的,
,
,
,
当时,y随x的增大而增大,
故当时,y的最大值为,
故应选:C.
8.答案:C
解析:建立如图所示坐标系,抛物线的顶点坐标为,
设抛物线解析式为
抛物线过,
把代入
,
两壁灯之间的水平距离为,
故选:C.
9.答案:
解析:由函数图象可知抛物线与x轴交于,,
∴关于x的方程的解是,,
故答案为:,.
10.答案:11
解析:对于,令,则,
解得:,(舍),
,
米.
故答案为:11.
11.答案:
解析:∵关于x的一元二次方程无实数根,
∴抛物线与没有交点,
∵抛物线的顶点坐标是,
∴.
故答案为:.
12.答案:8
解析:由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,
当喷头高2.5m时,可设,
将代入解析式得出①,
喷头高4m时,可设,
将(3,0)代入解析式得②,
联立可求出,,
设喷头高为h时,水柱落点距O点4m,
∴此时的解析式为,
将代入可得,
解得.
故答案为:8.
13.答案:每件售价提高4元时,才能使一天的利润最大,最大利润是360元
解析:设每件售价提高x元,每天的利润为y元,则每件的利润为元,每天的销售量为件,
∴,解得:.
依题意有:.
∵,∴当时,y最大,最大值为360,
∴每件售价提高4元时,才能使一天的利润最大,最大利润是360元.
14.答案:(1)见解析
(2)
解析:(1)由题意,得,
无论m取任何实数时,该函数图象与x轴总有交点.
(2),,.
该函数的图象与x轴交点的横坐标均为正数,
,即.
m取最小整数;.
同课章节目录
