人教版八年级数学上册第十一章《三角形》综合复习题(含答案)
文档属性
| 名称 | 人教版八年级数学上册第十一章《三角形》综合复习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 772.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 22:57:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册第十一章《三角形》综合复习题(含答案)
一.选择题(共10小题,满分30分,每小题3分)
1.三角形的重心是三角形的( )
A.三条角平分线的交点 B.一条边的中线与另一边的高的交点
C.三条高的交点 D.三条中线的交点
2.下列长度的三条线段能组成三角形的是( )
A.2、3、5 B.5、15、8 C.10、16、8 D.3、6、9
3.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上( )根木条.
A.1 B.2 C.3 D.4
4.如图,足球的表面是由正五边形和正六边形拼接而成,其中黑皮的正五边形有12块,白皮的正六边形有20块.如图,足球图片中的一块黑色皮块的内角和是( )
A.180° B.360° C.540° D.720°
(3题) (4题) (7题) (9题)
5.下列关于三角形的角平分线、中线、高的说法正确的是( )
A.三角形的角平分线、中线、高都是线段
B.三角形的高是直线,角平分线是射线,中线是线段
C.三角形的角平分线、中线、高都在三角形内部
D.三角形的角平分线、中线在三角形内部,高在三角形外部
6.若一个三角形的三个内角的度数比为3:4:7,则这个三角形为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
7.如图,在△ABC中,BE⊥AC于点E,AD⊥CB,交CB的延长线于点D,BC=10,AD=6,BE=5,则AC的长为( )
A.12 B.11 C.10 D.9
8.如果等腰三角形的各边长是整数,周长为9,那么这样的等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在△ABC中,AD⊥BC于点D,BE平分∠ABC交AD于点E.若∠EBD=30°,∠BAC=70°,则∠DAC=( )
A.60° B.50° C.40° D.45°
10.如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45° B.50° C.55° D.80°
二.填空题(共5小题,满分15分,每小题3分)
11.已知三角形的三边长都是整数,其中两边长分别为5和1,则它的周长为 .
12.若a、b、c为三角形的三边,且a、b满足(b﹣2)2=0,则第三边c的取值范围是 .
13.若一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来的多边形的边数是 .
(10题) (14题) (15题)
14.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=50°,则∠BOE的度数为 .
15.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为 .
三.解答题(共8小题,满分75分)
16.(9分)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
17.(9分)在一个正多边形中,一个内角是它相邻的一个外角的3倍.
(1)求这个多边形的每一个外角的度数.
(2)求这个多边形的边数.
18.(9分)如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
19.(9分)如图,在△ABC中,AD是高,∠DAC=10°,AE是△ABC外角∠MAC的平分线,交BC的延长线于点E,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.
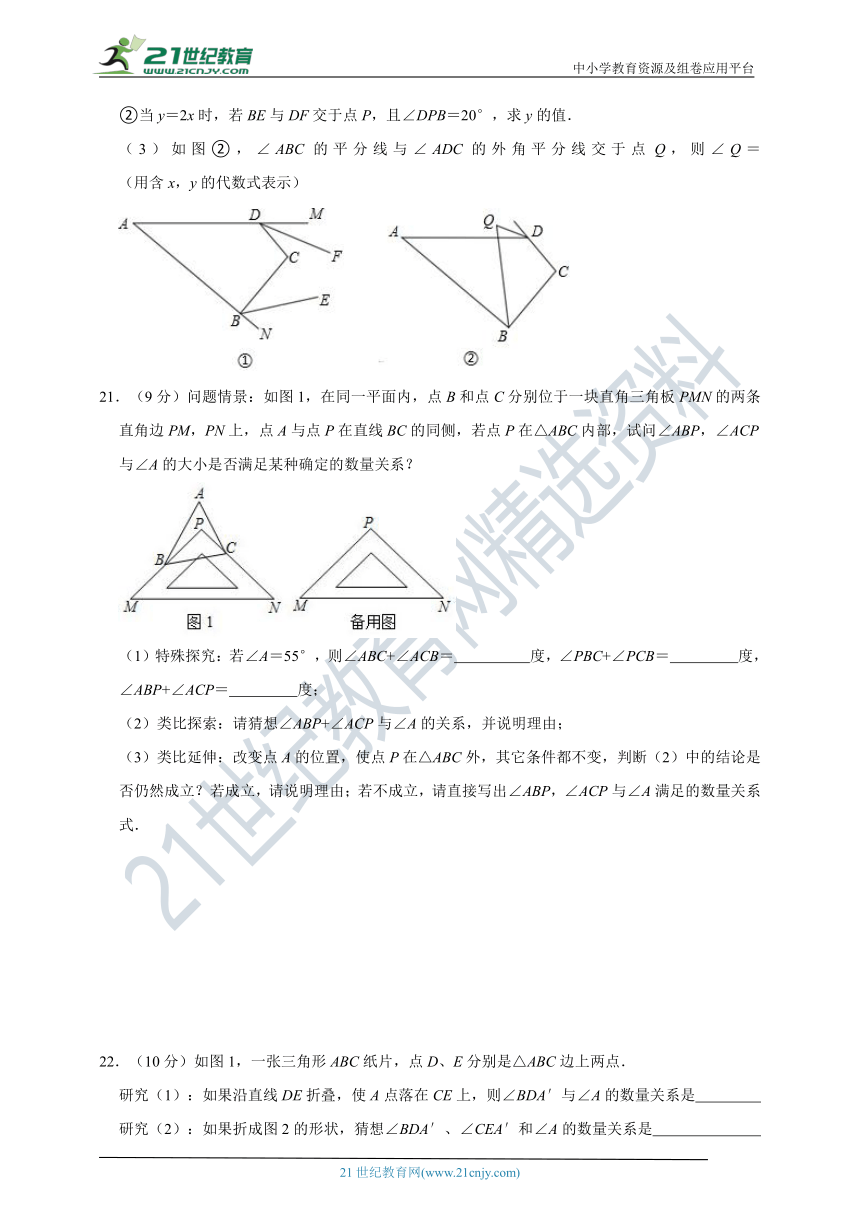
20.(9分)如图①,在四边形ABCD中,∠A=x°,∠C=y°.
(1)∠ABC+∠ADC= °(用含x,y的代数式表示)
(2)BE、DF分别为∠ABC、∠ADC的外角平分线,
①若BE∥DF,x=30,则y= ;
②当y=2x时,若BE与DF交于点P,且∠DPB=20°,求y的值.
(3)如图②,∠ABC的平分线与∠ADC的外角平分线交于点Q,则∠Q= (用含x,y的代数式表示)
21.(9分)问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板PMN的两条直角边PM,PN上,点A与点P在直线BC的同侧,若点P在△ABC内部,试问∠ABP,∠ACP与∠A的大小是否满足某种确定的数量关系?
(1)特殊探究:若∠A=55°,则∠ABC+∠ACB= 度,∠PBC+∠PCB= 度,∠ABP+∠ACP= 度;
(2)类比探索:请猜想∠ABP+∠ACP与∠A的关系,并说明理由;
(3)类比延伸:改变点A的位置,使点P在△ABC外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出∠ABP,∠ACP与∠A满足的数量关系式.
22.(10分)如图1,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 .
23.(11分)如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后,A、B两点的坐标;
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值:若发生变化,请说明理由.
(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵三角形的重心是三角形三条边中线的交点,
∴选项D正确.
2.解:根据三角形的三边关系,知
A、2+3=5,不能组成三角形;
B、5+8=13<15,不能组成三角形;
C、10+8=18>16,能组成三角形;
D、3+6=9,不能组成三角形.
故选:C.
3.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
故选:C.
4.解:∵黑皮是正五边形,
∴一块黑色皮块的内角和=(5﹣2)×180°=540°.
故选:C.
5.解:A、三角形的角平分线、中线、高都是线段,说法正确,符合题意;
B、三角形的高是线段,角平分线是线段,中线是线段,故本选项说法错误,不符合题意;
C、三角形的角平分线、中线都在三角形内部,但高不一定都在三角形内部,故本选项说法错误,不符合题意;
D、三角形的角平分线、中线在三角形内部,高可能在三角形内部、边上或外部,故本选项说法错误,不符合题意;
故选:A.
6.解:设一份为k°,则三个内角的度数分别为3k°,4k°,7k°,
则3k°+4k°+7k°=180°,
解得7k°=90°.
所以最大的内角是90°.
故三角形是直角三角形,
故选:A.
7.解:BD=x,AC=a,
∵S△ABD6x=3x,S△ABC5a=2.5a,S△ADC6(x+10)=3x+30,
又∵S△ABD+S△ABC=S△ADC,
∴3x+2.5a=3x+30,
解得:a=12,
∴AC的长为12.
故选:A.
8.解:设等腰三角形的腰长为x,则底边长为9﹣2x,
由题意得:,
解得:2.25<x<4.5,
∵x为整数,
∴x=3或4,
当x=3时,9﹣2x=3,等腰三角形的三边长分别为3,3,3;
当x=4时,9﹣2x=1,等腰三角形的三边长分别为4,4,1;
综上所述:这样的等腰三角形有2个,
故选:B.
9.解:∵BE平分∠ABC交AD于点E,∠EBD=30°,
∴∠ABC=2∠EBD=60°,
∵∠BAC=70°,∠ABC+∠BAC+∠C=180°,
∴∠C=50°,
∵AD⊥BC于点D,
∴∠ADC=90°,
∵∠ADC+∠C+∠DAC=180°,
∴∠DAC=40°,
故选:C.
10.解:连接AC并延长交EF于点G.
∵AB∥CF,
∴∠BAC=∠FCG,
∵AD∥CE,
∴∠DAC=∠ECG,
∴∠BAD=∠BAC+∠DAC=∠FCG+∠ECG=∠ECF,
在△CEF中,∠E=80°,∠F=55°,
∴∠ECF=180°﹣∠E﹣∠F=180°﹣80°﹣55°=45°,
∴∠BAD=∠ECF=45°.
故选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.已知三角形的三边长都是整数,其中两边长分别为5和1,则它的周长为 11 .
解:∵三角形的两边的长为5和1,
∴第三边的取值范围是4<x<6,
∵三角形的三边长都是整数,
∴第三边的长为5,
∴周长为:5+5+1=11,
故答案为:11.
12.若a、b、c为三角形的三边,且a、b满足(b﹣2)2=0,则第三边c的取值范围是 1<c<5 .
解:由题意得,a2﹣9=0,b﹣2=0,
解得a=3,b=2,
∵3﹣2=1,3+2=5,
∴1<c<5.
故答案为:1<c<5.
13.若一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来的多边形的边数是 10,11或12 .
解:多边形的内角和可以表示成(n﹣2) 180°(n≥3且n是整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,
根据(n﹣2) 180°=1620°,
解得:n=11,
则多边形的边数是10,11或12.
故答案为10,11或12.
14.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=50°,则∠BOE的度数为 65° .
解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠1∠ABC,∠2∠ACB,
∴∠1+∠2∠ABC∠ACB(∠ABC+∠ACB)=65°,
∴∠BOC=180°﹣65°=115°,
∴∠BOE=180°﹣115°=65°,
故答案为:65°.
15.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为 20°或60° .
解:如图所示,当∠BFD=90°时,
∵AD是△ABC的角平分线,∠BAC=60°,
∴∠BAD=30°,
∴Rt△ADF中,∠ADF=60°;
如图,当∠BDF=90°时,
同理可得∠BAD=30°,
∵CE是△ABC的高,∠BCE=50°,
∴∠BFD=∠BCE=50°,
∴∠ADF=∠BFD﹣∠BAD=20°,
综上所述,∠ADF的度数为20°或60°.
故答案为:20°或60°.
三.解答题(共8小题,满分75分)
16.(9分)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
17.(9分)在一个正多边形中,一个内角是它相邻的一个外角的3倍.
(1)求这个多边形的每一个外角的度数.
(2)求这个多边形的边数.
解:(1)设这个多边形的每一个外角的度数为x度.根据题意,得:
3x+x=180,
解得x=45.
故这个多边形的每一个外角的度数为45°;
(2)360°÷45°=8.
故这个多边形的边数为8.
18.(9分)如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
解:(1)∵∠A=50°,∠C=30°,
∴∠BDO=∠A+∠C=80°;
∵∠BOD=70°,
∴∠B=180°﹣∠BDO﹣∠BOD=30°;
(2)∠BOC=∠A+∠B+∠C.
理由:∵∠BEC=∠A+∠B,
∴∠BOC=∠BEC+∠C=∠A+∠B+∠C.
19.(9分)如图,在△ABC中,AD是高,∠DAC=10°,AE是△ABC外角∠MAC的平分线,交BC的延长线于点E,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.
解:∵AD是高,
∴∠ADB=90°,
∵∠ABC=46°,
∴∠BAD=90°﹣∠ABC=90°﹣46°=44°,
∵∠DAC=10°,
∴∠BAC=∠BAD+∠DAC=44°+10°=54°,
∴∠MAC=180°﹣∠BAC=126°,
∵AE是△ABC外角∠MAC的平分线,
∴∠CAEMAC=63°,
∴∠BAF=∠BAC+∠CAE=54°+63°=117°,
∵∠ABC=46°,BF平分∠ABC,
∴∠ABF∠ABC=23°,
∴∠AFB=180°﹣∠ABF﹣∠BAF=180°﹣23°﹣117°=40°.
20.(9分)如图①,在四边形ABCD中,∠A=x°,∠C=y°.
(1)∠ABC+∠ADC= (360﹣x﹣y) °(用含x,y的代数式表示)
(2)BE、DF分别为∠ABC、∠ADC的外角平分线,
①若BE∥DF,x=30,则y= 30 ;
②当y=2x时,若BE与DF交于点P,且∠DPB=20°,求y的值.
(3)如图②,∠ABC的平分线与∠ADC的外角平分线交于点Q,则∠Q= [90(x﹣y)]° (用含x,y的代数式表示)
解:(1)在四边形ABCD中,∠ABC+∠ADC=360°﹣∠A﹣∠DCB=360°﹣x°﹣y°.
故答案为:(360﹣x﹣y).
(2)①如图1中,
∵BE∥DF,
∴∠C=∠CDF+∠CBE=y°,
∵BE、DF分别为∠ABC、∠ADC的外角平分线,
∴∠MDC+∠CBN=2(∠CDF+∠CBE)=(2y)°,
∵∠ADC+∠ABC=360°﹣30°﹣y°,
∵∠ADC+∠MDC=180°,∠ABC+∠CBN=180°,
∴360°﹣30°﹣y°+(2y)°=360°,
∴y=30.
故答案为30.
②如图2中,延长BC交PD于Q.
由(1)可知:∠ABC+∠ADC=(360﹣x﹣y)°,
∵∠ADC+∠MDC=180°,∠ABC+∠NBC=180°,
∴∠NBC+∠MDC=(x+y)°,
∵BE、DF分别为∠ABC、∠ADC的外角平分线,
∴∠PBC∠NBC,∠PDC∠MDC,
∴∠PBC+∠PDC=[(x+y)]°,
∵∠BCD=∠PDC+∠CQD,∠CQD=∠PBC+∠P,
∴∠BCD=∠PDC+∠PBC+∠P,
∴y=20(x+y),即y﹣x=40,
∵y=2x,
∴x=40,y=80.
(3)如图②中,
由题意:∠DNQ=∠ANB=180°﹣x°∠ABC,∠QDN(180°﹣∠ADC),
∴∠Q=180°﹣∠DNQ﹣∠QDN=180°﹣(180°﹣x°∠ABC)(180°﹣∠ADC)
=x°(∠ABC+∠ADC)﹣90°
=x°+180°(x+y)°﹣90°
=[90(x﹣y)]°.
故答案为:[90(x﹣y)]°.
21.(9分)问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板PMN的两条直角边PM,PN上,点A与点P在直线BC的同侧,若点P在△ABC内部,试问∠ABP,∠ACP与∠A的大小是否满足某种确定的数量关系?
(1)特殊探究:若∠A=55°,则∠ABC+∠ACB= 125 度,∠PBC+∠PCB= 90 度,∠ABP+∠ACP= 35 度;
(2)类比探索:请猜想∠ABP+∠ACP与∠A的关系,并说明理由;
(3)类比延伸:改变点A的位置,使点P在△ABC外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出∠ABP,∠ACP与∠A满足的数量关系式.
解:(1)由题意:∠ABC+∠ACB=125度,∠PBC+∠PCB=90度,
∠ABP+∠ACP=35度.
故答案为125,90,35.
(2)猜想:∠ABP+∠ACP=90°﹣∠A.
理由:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠ABC=∠ABP+∠PBC,∠ACB=∠ACP+∠PCB,
∴(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°﹣∠A,
∴(∠ABP+∠ACP)+(∠PBC+∠PCB)=180°﹣∠A,
又∵在Rt△PBC中,∠P=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABP+∠ACP)+90°=180°﹣∠A,
∴∠ABP+∠ACP=90°﹣∠A.
(3)判断:(2)中的结论不成立.
①如图3﹣1中,结论:∠A+∠ACP﹣∠ABP=90°.
理由:设AB交PN于O.
∵∠AOC=∠BOP,
∴∠A+∠ACP=90°+∠ABP,
∴∠A+∠ACP﹣∠ABP=90°.
②如图3﹣2中,结论:∠A+∠ABP﹣∠ACP=90°.证明方法类似①
③如图3﹣3中,结论:∠A﹣∠ABP﹣∠ACP=90°.
理由:∵∠A+∠ABC+∠ACB=180°,∠P+∠ABP+∠ACP+∠ABC+∠ACB=180°,
∴∠A=∠P+∠ABP+∠ACP,
∴∠A﹣∠ABP﹣∠ACP=90°.
22.(10分)如图1,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是 ∠BDA′=2∠A
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 ∠BDA′+∠CEA′=2∠A
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 ∠BDA′﹣∠CEA′=2∠A .
解:(1)∠BDA′与∠A的数量关系是∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°,
∴∠A+∠DA′E=360°﹣∠ADA′﹣∠A′EA,
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°,
∴∠BDA′+∠CEA′=360°﹣∠ADA′﹣∠A′EA,
∴∠BDA′+∠CEA′=∠A+∠DA′E,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′﹣∠CEA′=2∠A.
理由:DA′交AC于点F,
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′,
∴∠BDA′=∠A+∠A′+∠CEA′,
∴∠BDA′﹣∠CEA′=∠A+∠A′,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠BDA′﹣∠CEA′=2∠A.
故答案为:∠BDA′=2∠A;∠BDA′+∠CEA′=2∠A;∠BDA′﹣∠CEA′=2∠A.
23.(11分)如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后,A、B两点的坐标;
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值:若发生变化,请说明理由.
(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.
解:(1)由题意得,,
解得,,
∴A(﹣1,0),B(0,2);
(2)∠P的大小不发生变化,
∵∠P=180°﹣∠PAB﹣∠PBA
=180°(∠EAB+∠FBA)
=180°(∠ABO+90°+∠BAO+90°)
=180°(180°+90°)
=180°﹣135°
=45°,
∴∠P的大小不会发生变化;
(3)∠AGH=∠BGC,
理由如下:作GM⊥BF于点M.
由已知得:∠AGH=90°∠EAC
=90°(180°﹣∠BAC)
∠BAC,
∠BGC=∠BGM﹣∠CGM
=90°∠ABC﹣(90°∠ACF)
(∠ACF﹣∠ABC)
∠BAC
∴∠AGH=∠BGC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上册第十一章《三角形》综合复习题(含答案)
一.选择题(共10小题,满分30分,每小题3分)
1.三角形的重心是三角形的( )
A.三条角平分线的交点 B.一条边的中线与另一边的高的交点
C.三条高的交点 D.三条中线的交点
2.下列长度的三条线段能组成三角形的是( )
A.2、3、5 B.5、15、8 C.10、16、8 D.3、6、9
3.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上( )根木条.
A.1 B.2 C.3 D.4
4.如图,足球的表面是由正五边形和正六边形拼接而成,其中黑皮的正五边形有12块,白皮的正六边形有20块.如图,足球图片中的一块黑色皮块的内角和是( )
A.180° B.360° C.540° D.720°
(3题) (4题) (7题) (9题)
5.下列关于三角形的角平分线、中线、高的说法正确的是( )
A.三角形的角平分线、中线、高都是线段
B.三角形的高是直线,角平分线是射线,中线是线段
C.三角形的角平分线、中线、高都在三角形内部
D.三角形的角平分线、中线在三角形内部,高在三角形外部
6.若一个三角形的三个内角的度数比为3:4:7,则这个三角形为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
7.如图,在△ABC中,BE⊥AC于点E,AD⊥CB,交CB的延长线于点D,BC=10,AD=6,BE=5,则AC的长为( )
A.12 B.11 C.10 D.9
8.如果等腰三角形的各边长是整数,周长为9,那么这样的等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在△ABC中,AD⊥BC于点D,BE平分∠ABC交AD于点E.若∠EBD=30°,∠BAC=70°,则∠DAC=( )
A.60° B.50° C.40° D.45°
10.如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45° B.50° C.55° D.80°
二.填空题(共5小题,满分15分,每小题3分)
11.已知三角形的三边长都是整数,其中两边长分别为5和1,则它的周长为 .
12.若a、b、c为三角形的三边,且a、b满足(b﹣2)2=0,则第三边c的取值范围是 .
13.若一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来的多边形的边数是 .
(10题) (14题) (15题)
14.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=50°,则∠BOE的度数为 .
15.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为 .
三.解答题(共8小题,满分75分)
16.(9分)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
17.(9分)在一个正多边形中,一个内角是它相邻的一个外角的3倍.
(1)求这个多边形的每一个外角的度数.
(2)求这个多边形的边数.
18.(9分)如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
19.(9分)如图,在△ABC中,AD是高,∠DAC=10°,AE是△ABC外角∠MAC的平分线,交BC的延长线于点E,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.
20.(9分)如图①,在四边形ABCD中,∠A=x°,∠C=y°.
(1)∠ABC+∠ADC= °(用含x,y的代数式表示)
(2)BE、DF分别为∠ABC、∠ADC的外角平分线,
①若BE∥DF,x=30,则y= ;
②当y=2x时,若BE与DF交于点P,且∠DPB=20°,求y的值.
(3)如图②,∠ABC的平分线与∠ADC的外角平分线交于点Q,则∠Q= (用含x,y的代数式表示)
21.(9分)问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板PMN的两条直角边PM,PN上,点A与点P在直线BC的同侧,若点P在△ABC内部,试问∠ABP,∠ACP与∠A的大小是否满足某种确定的数量关系?
(1)特殊探究:若∠A=55°,则∠ABC+∠ACB= 度,∠PBC+∠PCB= 度,∠ABP+∠ACP= 度;
(2)类比探索:请猜想∠ABP+∠ACP与∠A的关系,并说明理由;
(3)类比延伸:改变点A的位置,使点P在△ABC外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出∠ABP,∠ACP与∠A满足的数量关系式.
22.(10分)如图1,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 .
23.(11分)如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后,A、B两点的坐标;
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值:若发生变化,请说明理由.
(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵三角形的重心是三角形三条边中线的交点,
∴选项D正确.
2.解:根据三角形的三边关系,知
A、2+3=5,不能组成三角形;
B、5+8=13<15,不能组成三角形;
C、10+8=18>16,能组成三角形;
D、3+6=9,不能组成三角形.
故选:C.
3.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
故选:C.
4.解:∵黑皮是正五边形,
∴一块黑色皮块的内角和=(5﹣2)×180°=540°.
故选:C.
5.解:A、三角形的角平分线、中线、高都是线段,说法正确,符合题意;
B、三角形的高是线段,角平分线是线段,中线是线段,故本选项说法错误,不符合题意;
C、三角形的角平分线、中线都在三角形内部,但高不一定都在三角形内部,故本选项说法错误,不符合题意;
D、三角形的角平分线、中线在三角形内部,高可能在三角形内部、边上或外部,故本选项说法错误,不符合题意;
故选:A.
6.解:设一份为k°,则三个内角的度数分别为3k°,4k°,7k°,
则3k°+4k°+7k°=180°,
解得7k°=90°.
所以最大的内角是90°.
故三角形是直角三角形,
故选:A.
7.解:BD=x,AC=a,
∵S△ABD6x=3x,S△ABC5a=2.5a,S△ADC6(x+10)=3x+30,
又∵S△ABD+S△ABC=S△ADC,
∴3x+2.5a=3x+30,
解得:a=12,
∴AC的长为12.
故选:A.
8.解:设等腰三角形的腰长为x,则底边长为9﹣2x,
由题意得:,
解得:2.25<x<4.5,
∵x为整数,
∴x=3或4,
当x=3时,9﹣2x=3,等腰三角形的三边长分别为3,3,3;
当x=4时,9﹣2x=1,等腰三角形的三边长分别为4,4,1;
综上所述:这样的等腰三角形有2个,
故选:B.
9.解:∵BE平分∠ABC交AD于点E,∠EBD=30°,
∴∠ABC=2∠EBD=60°,
∵∠BAC=70°,∠ABC+∠BAC+∠C=180°,
∴∠C=50°,
∵AD⊥BC于点D,
∴∠ADC=90°,
∵∠ADC+∠C+∠DAC=180°,
∴∠DAC=40°,
故选:C.
10.解:连接AC并延长交EF于点G.
∵AB∥CF,
∴∠BAC=∠FCG,
∵AD∥CE,
∴∠DAC=∠ECG,
∴∠BAD=∠BAC+∠DAC=∠FCG+∠ECG=∠ECF,
在△CEF中,∠E=80°,∠F=55°,
∴∠ECF=180°﹣∠E﹣∠F=180°﹣80°﹣55°=45°,
∴∠BAD=∠ECF=45°.
故选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.已知三角形的三边长都是整数,其中两边长分别为5和1,则它的周长为 11 .
解:∵三角形的两边的长为5和1,
∴第三边的取值范围是4<x<6,
∵三角形的三边长都是整数,
∴第三边的长为5,
∴周长为:5+5+1=11,
故答案为:11.
12.若a、b、c为三角形的三边,且a、b满足(b﹣2)2=0,则第三边c的取值范围是 1<c<5 .
解:由题意得,a2﹣9=0,b﹣2=0,
解得a=3,b=2,
∵3﹣2=1,3+2=5,
∴1<c<5.
故答案为:1<c<5.
13.若一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来的多边形的边数是 10,11或12 .
解:多边形的内角和可以表示成(n﹣2) 180°(n≥3且n是整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,
根据(n﹣2) 180°=1620°,
解得:n=11,
则多边形的边数是10,11或12.
故答案为10,11或12.
14.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=50°,则∠BOE的度数为 65° .
解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠1∠ABC,∠2∠ACB,
∴∠1+∠2∠ABC∠ACB(∠ABC+∠ACB)=65°,
∴∠BOC=180°﹣65°=115°,
∴∠BOE=180°﹣115°=65°,
故答案为:65°.
15.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为 20°或60° .
解:如图所示,当∠BFD=90°时,
∵AD是△ABC的角平分线,∠BAC=60°,
∴∠BAD=30°,
∴Rt△ADF中,∠ADF=60°;
如图,当∠BDF=90°时,
同理可得∠BAD=30°,
∵CE是△ABC的高,∠BCE=50°,
∴∠BFD=∠BCE=50°,
∴∠ADF=∠BFD﹣∠BAD=20°,
综上所述,∠ADF的度数为20°或60°.
故答案为:20°或60°.
三.解答题(共8小题,满分75分)
16.(9分)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
17.(9分)在一个正多边形中,一个内角是它相邻的一个外角的3倍.
(1)求这个多边形的每一个外角的度数.
(2)求这个多边形的边数.
解:(1)设这个多边形的每一个外角的度数为x度.根据题意,得:
3x+x=180,
解得x=45.
故这个多边形的每一个外角的度数为45°;
(2)360°÷45°=8.
故这个多边形的边数为8.
18.(9分)如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
解:(1)∵∠A=50°,∠C=30°,
∴∠BDO=∠A+∠C=80°;
∵∠BOD=70°,
∴∠B=180°﹣∠BDO﹣∠BOD=30°;
(2)∠BOC=∠A+∠B+∠C.
理由:∵∠BEC=∠A+∠B,
∴∠BOC=∠BEC+∠C=∠A+∠B+∠C.
19.(9分)如图,在△ABC中,AD是高,∠DAC=10°,AE是△ABC外角∠MAC的平分线,交BC的延长线于点E,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.
解:∵AD是高,
∴∠ADB=90°,
∵∠ABC=46°,
∴∠BAD=90°﹣∠ABC=90°﹣46°=44°,
∵∠DAC=10°,
∴∠BAC=∠BAD+∠DAC=44°+10°=54°,
∴∠MAC=180°﹣∠BAC=126°,
∵AE是△ABC外角∠MAC的平分线,
∴∠CAEMAC=63°,
∴∠BAF=∠BAC+∠CAE=54°+63°=117°,
∵∠ABC=46°,BF平分∠ABC,
∴∠ABF∠ABC=23°,
∴∠AFB=180°﹣∠ABF﹣∠BAF=180°﹣23°﹣117°=40°.
20.(9分)如图①,在四边形ABCD中,∠A=x°,∠C=y°.
(1)∠ABC+∠ADC= (360﹣x﹣y) °(用含x,y的代数式表示)
(2)BE、DF分别为∠ABC、∠ADC的外角平分线,
①若BE∥DF,x=30,则y= 30 ;
②当y=2x时,若BE与DF交于点P,且∠DPB=20°,求y的值.
(3)如图②,∠ABC的平分线与∠ADC的外角平分线交于点Q,则∠Q= [90(x﹣y)]° (用含x,y的代数式表示)
解:(1)在四边形ABCD中,∠ABC+∠ADC=360°﹣∠A﹣∠DCB=360°﹣x°﹣y°.
故答案为:(360﹣x﹣y).
(2)①如图1中,
∵BE∥DF,
∴∠C=∠CDF+∠CBE=y°,
∵BE、DF分别为∠ABC、∠ADC的外角平分线,
∴∠MDC+∠CBN=2(∠CDF+∠CBE)=(2y)°,
∵∠ADC+∠ABC=360°﹣30°﹣y°,
∵∠ADC+∠MDC=180°,∠ABC+∠CBN=180°,
∴360°﹣30°﹣y°+(2y)°=360°,
∴y=30.
故答案为30.
②如图2中,延长BC交PD于Q.
由(1)可知:∠ABC+∠ADC=(360﹣x﹣y)°,
∵∠ADC+∠MDC=180°,∠ABC+∠NBC=180°,
∴∠NBC+∠MDC=(x+y)°,
∵BE、DF分别为∠ABC、∠ADC的外角平分线,
∴∠PBC∠NBC,∠PDC∠MDC,
∴∠PBC+∠PDC=[(x+y)]°,
∵∠BCD=∠PDC+∠CQD,∠CQD=∠PBC+∠P,
∴∠BCD=∠PDC+∠PBC+∠P,
∴y=20(x+y),即y﹣x=40,
∵y=2x,
∴x=40,y=80.
(3)如图②中,
由题意:∠DNQ=∠ANB=180°﹣x°∠ABC,∠QDN(180°﹣∠ADC),
∴∠Q=180°﹣∠DNQ﹣∠QDN=180°﹣(180°﹣x°∠ABC)(180°﹣∠ADC)
=x°(∠ABC+∠ADC)﹣90°
=x°+180°(x+y)°﹣90°
=[90(x﹣y)]°.
故答案为:[90(x﹣y)]°.
21.(9分)问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板PMN的两条直角边PM,PN上,点A与点P在直线BC的同侧,若点P在△ABC内部,试问∠ABP,∠ACP与∠A的大小是否满足某种确定的数量关系?
(1)特殊探究:若∠A=55°,则∠ABC+∠ACB= 125 度,∠PBC+∠PCB= 90 度,∠ABP+∠ACP= 35 度;
(2)类比探索:请猜想∠ABP+∠ACP与∠A的关系,并说明理由;
(3)类比延伸:改变点A的位置,使点P在△ABC外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出∠ABP,∠ACP与∠A满足的数量关系式.
解:(1)由题意:∠ABC+∠ACB=125度,∠PBC+∠PCB=90度,
∠ABP+∠ACP=35度.
故答案为125,90,35.
(2)猜想:∠ABP+∠ACP=90°﹣∠A.
理由:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠ABC=∠ABP+∠PBC,∠ACB=∠ACP+∠PCB,
∴(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°﹣∠A,
∴(∠ABP+∠ACP)+(∠PBC+∠PCB)=180°﹣∠A,
又∵在Rt△PBC中,∠P=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABP+∠ACP)+90°=180°﹣∠A,
∴∠ABP+∠ACP=90°﹣∠A.
(3)判断:(2)中的结论不成立.
①如图3﹣1中,结论:∠A+∠ACP﹣∠ABP=90°.
理由:设AB交PN于O.
∵∠AOC=∠BOP,
∴∠A+∠ACP=90°+∠ABP,
∴∠A+∠ACP﹣∠ABP=90°.
②如图3﹣2中,结论:∠A+∠ABP﹣∠ACP=90°.证明方法类似①
③如图3﹣3中,结论:∠A﹣∠ABP﹣∠ACP=90°.
理由:∵∠A+∠ABC+∠ACB=180°,∠P+∠ABP+∠ACP+∠ABC+∠ACB=180°,
∴∠A=∠P+∠ABP+∠ACP,
∴∠A﹣∠ABP﹣∠ACP=90°.
22.(10分)如图1,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是 ∠BDA′=2∠A
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 ∠BDA′+∠CEA′=2∠A
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 ∠BDA′﹣∠CEA′=2∠A .
解:(1)∠BDA′与∠A的数量关系是∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°,
∴∠A+∠DA′E=360°﹣∠ADA′﹣∠A′EA,
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°,
∴∠BDA′+∠CEA′=360°﹣∠ADA′﹣∠A′EA,
∴∠BDA′+∠CEA′=∠A+∠DA′E,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′﹣∠CEA′=2∠A.
理由:DA′交AC于点F,
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′,
∴∠BDA′=∠A+∠A′+∠CEA′,
∴∠BDA′﹣∠CEA′=∠A+∠A′,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠BDA′﹣∠CEA′=2∠A.
故答案为:∠BDA′=2∠A;∠BDA′+∠CEA′=2∠A;∠BDA′﹣∠CEA′=2∠A.
23.(11分)如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后,A、B两点的坐标;
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值:若发生变化,请说明理由.
(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.
解:(1)由题意得,,
解得,,
∴A(﹣1,0),B(0,2);
(2)∠P的大小不发生变化,
∵∠P=180°﹣∠PAB﹣∠PBA
=180°(∠EAB+∠FBA)
=180°(∠ABO+90°+∠BAO+90°)
=180°(180°+90°)
=180°﹣135°
=45°,
∴∠P的大小不会发生变化;
(3)∠AGH=∠BGC,
理由如下:作GM⊥BF于点M.
由已知得:∠AGH=90°∠EAC
=90°(180°﹣∠BAC)
∠BAC,
∠BGC=∠BGM﹣∠CGM
=90°∠ABC﹣(90°∠ACF)
(∠ACF﹣∠ABC)
∠BAC
∴∠AGH=∠BGC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
