2.2.2 公式法 课件(共12张PPT)
文档属性
| 名称 | 2.2.2 公式法 课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 365.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 10:02:30 | ||
图片预览





文档简介
(共12张PPT)
2.2.2 公式法
运用配方法解一元二次方程时,我们对于每一个具体的方程,都重复使用了一些相同的计算步骤,这启发我们思考:能不能对一般形式的一元二次方程
ax2+bx+c=0(a ≠ 0)
使用配方法,求出这个方程的根呢?
对于方程
ax2+bx+c=0(a ≠ 0)
为了便于配方,在方程的两边同除以a,得
x2 + x+ =0.
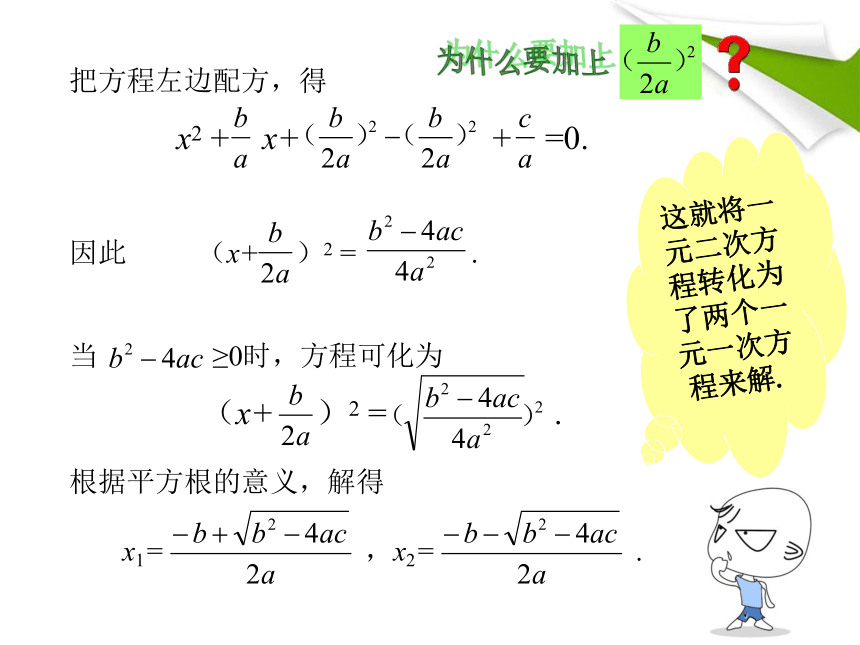
把方程左边配方,得
x2 + x+ + =0.
因此 (x+ )2 = .
当 ≥0时,方程可化为
(x+ )2 = .
根据平方根的意义,解得
x1= ,x2= .
这就将一元二次方程转化为了两个一元一次方程来解.
结论
一元二次方程 ax2+bx+c=0(a ≠ 0)在 ≥0的条件下,它的根为:
x= ( ≥0).
我们通常把这个式子叫做一元二次方程ax2+bx+c=0(a ≠ 0)的求根公式.今后我们可以运用一元二次方程的求根公式直接求每一个一元二次方程的根,这种解一元二次方程的方法叫作公式法.
例题讲解
例 1 用公式法解方程:x2-7x-18=0.
即
解
这里
例 2 用公式法解方程:x2+3= .
这里
移项,得
解
即
先将方程化为一般形式,再确定a,b,c的值.
此时方程的两个实数根相等.
求根公式 : X=
一、由配方法解一般的一元二次方程 ax2+bx+c=0 (a≠0) 若 b2-4ac≥0 得
二、用公式法解一元二次方程的一般步骤:
1、把方程化成一般形式, 并写出a,b,c的值;
2、求出b2-4ac的值;
3、代入求根公式 :
X=
(a≠0, b2-4ac≥0)
4、写出方程的解: x1= , x2=
四、计算一定要细心,尤其
是计算b2-4ac的值和代入公式
时,符号不要弄错.
三、当 b2-4ac=0时,一元二次
方程有两个相等的实数根.
用公式法解下列方程:
(2)x2+4x+8=4x+11;
随堂练习
(3)x(2x-4)=5-8x;
随堂练习
2.2.2 公式法
运用配方法解一元二次方程时,我们对于每一个具体的方程,都重复使用了一些相同的计算步骤,这启发我们思考:能不能对一般形式的一元二次方程
ax2+bx+c=0(a ≠ 0)
使用配方法,求出这个方程的根呢?
对于方程
ax2+bx+c=0(a ≠ 0)
为了便于配方,在方程的两边同除以a,得
x2 + x+ =0.
把方程左边配方,得
x2 + x+ + =0.
因此 (x+ )2 = .
当 ≥0时,方程可化为
(x+ )2 = .
根据平方根的意义,解得
x1= ,x2= .
这就将一元二次方程转化为了两个一元一次方程来解.
结论
一元二次方程 ax2+bx+c=0(a ≠ 0)在 ≥0的条件下,它的根为:
x= ( ≥0).
我们通常把这个式子叫做一元二次方程ax2+bx+c=0(a ≠ 0)的求根公式.今后我们可以运用一元二次方程的求根公式直接求每一个一元二次方程的根,这种解一元二次方程的方法叫作公式法.
例题讲解
例 1 用公式法解方程:x2-7x-18=0.
即
解
这里
例 2 用公式法解方程:x2+3= .
这里
移项,得
解
即
先将方程化为一般形式,再确定a,b,c的值.
此时方程的两个实数根相等.
求根公式 : X=
一、由配方法解一般的一元二次方程 ax2+bx+c=0 (a≠0) 若 b2-4ac≥0 得
二、用公式法解一元二次方程的一般步骤:
1、把方程化成一般形式, 并写出a,b,c的值;
2、求出b2-4ac的值;
3、代入求根公式 :
X=
(a≠0, b2-4ac≥0)
4、写出方程的解: x1= , x2=
四、计算一定要细心,尤其
是计算b2-4ac的值和代入公式
时,符号不要弄错.
三、当 b2-4ac=0时,一元二次
方程有两个相等的实数根.
用公式法解下列方程:
(2)x2+4x+8=4x+11;
随堂练习
(3)x(2x-4)=5-8x;
随堂练习
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
