2024-2025学年湖南省娄底市涟源市部分学校高二(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖南省娄底市涟源市部分学校高二(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 73.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 23:04:28 | ||
图片预览



文档简介
2024-2025学年湖南省娄底市涟源市部分学校高二(上)开学数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若,则( )
A. B. C. D.
2.复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.为了培养青少年无私奉献,服务社会,回馈社会的精神,某学校鼓励学生在假期去社会上的一些福利机构做义工某慈善机构抽查了其中名学生在一年内在福利机构做义工的时间单位:小时,绘制成如图所示的频率分布直方图,则的值为( )
A.
B.
C.
D.
4.若四边形满足:,且,则四边形的形状是( )
A. 矩形 B. 正方形 C. 等腰梯形 D. 菱形
5.抛掷两枚质地均匀的硬币,记事件“第一枚硬币正面朝上”,事件“第二枚硬币反面朝上”,事件“两枚硬币都正面朝上”,事件“至少一枚硬币反面朝上”则( )
A. 与独立 B. 与互斥 C. D.
6.已知内角,,所对边的长分别为,,,,则形状一定是( )
A. 等腰直角三角形 B. 等边三角形 C. 等腰三角形 D. 直角三角形
7.已知两个平面、,在下列条件下,可以判定平面与平面平行的是( )
A. 、都垂直于一个平面
B. 平面内有无数条直线与平面平行
C. 、是内两条直线,且,
D. 、是两条异面直线,且,,,
8.正三棱柱的底面边长为,侧棱长为,为中点,则三棱锥的体积为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知向量,,且,则下列说法正确的是( )
A. B.
C. 向量与夹角是 D.
10.若,,则下列结论正确的有( )
A. B. 若,则
C. 若,则 D. 若,则
11.如图所示,在正方体中,,分别是,的中点,是线段上的动点,则下列判断正确的是( )
A. 三棱锥的体积是定值
B. 过,,三点的平面截正方体所得的截面是六边形
C. 存在唯一的点,使得
D. 与平面所成的角为定值
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,,且,则 ______.
13.甲、乙两人独立解同一道数学题目,甲解出这道题目的概率是,乙解出这道题目的概率是,这道题被解出至少有一人解出来的概率是______.
14.在中,,满足此条件有两解,则边长度的取值范围为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,.
若与垂直,求实数的值;
已知,,,为平面内四点,且,,若,,三点共线,求实数的值.
16.本小题分
如图,在多面体中,四边形是菱形,平面,,,.
求证:平面;
求证:平面.
17.本小题分
在中,,,.
求值;
求角和的面积.
18.本小题分
某地区课改时实行高考新方案试点,规定:语文、数学和英语是必考科目,考生还要从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目为了解某校学生选科情况,现从高一、高二、高三学生中各随机选取了名学生作为样本进行调查,调查数据如下表,用频率估计概率.
选考情况 第门 第门 第门 第门 第门 第门
物理 化学 生物 历史 地理 政治
高一选科人数
高二选科人数
高三选科人数
已知该校高一年级有人,估计该学校高一年级学生中选考历史的人数;
现采用分层抽样的方式从样本中随机抽取三个年级中选择历史学科的名学生组成兴趣小组,再从这人中随机抽取名同学参加知识问答比赛,求这名参赛同学来自不同年级的概率;
假设三个年级选择选考科目是相互独立的为了解不同年级学生对各科目的选择倾向,现从高一、高二、高三样本中各随机选取名学生进行调查,求这名学生均选择了第门科目的概率.
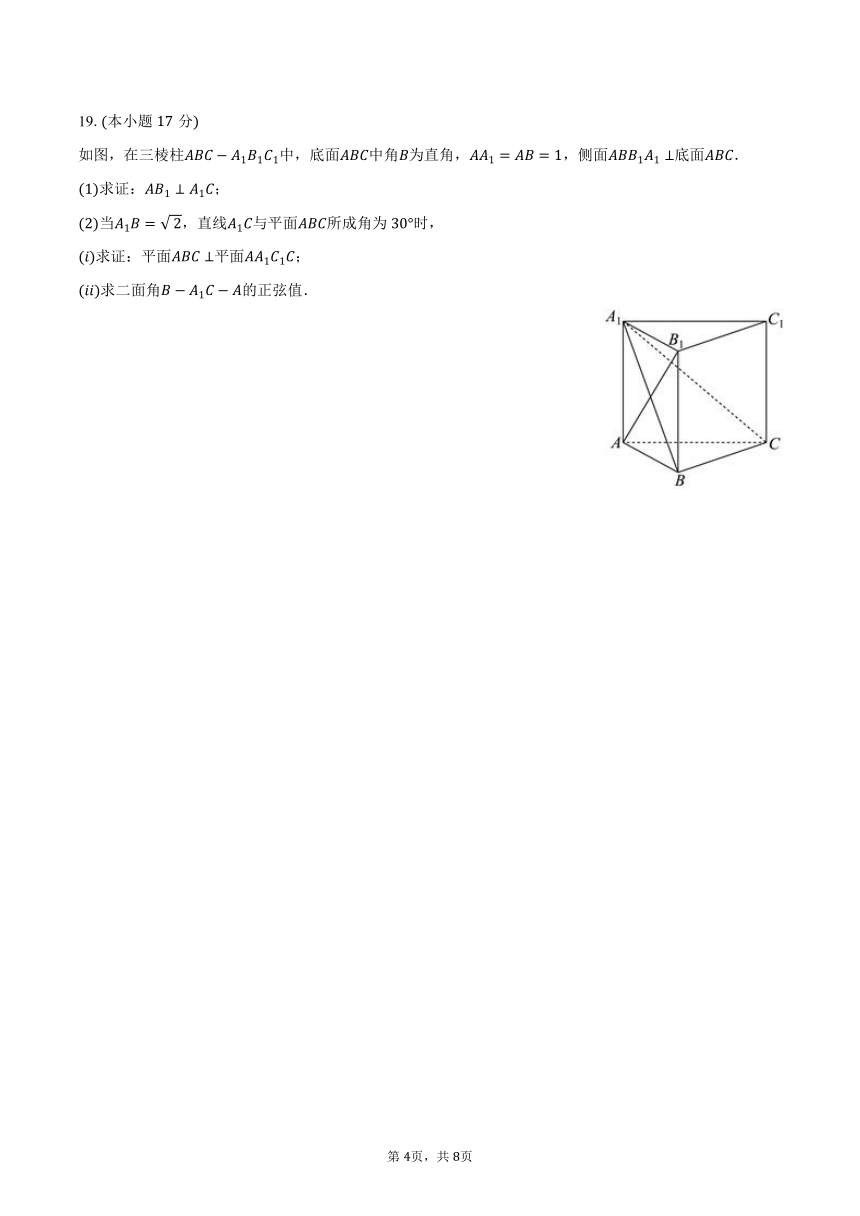
19.本小题分
如图,在三棱柱中,底面中角为直角,,侧面底面.
求证:;
当,直线与平面所成角为时,
求证:平面平面;
求二面角的正弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为,,
所以,
,
因为与垂直,所以,
解得;
因为,
,
所以,
,
因为,,三点共线,所以.
所以,
解得.
16.证明:连接,交于点,
四边形为菱形,,
平面,平面,,
,,平面,
平面;
证明:取的中点,连接,,
又为的中点,则,,
已知,,
则有,,四边形为平行四边形,
有,即有,
平面,平面,
平面.
17.解:因为,
由正弦定理可得:,
在中,可得,,
可得,
又因为,,
由余弦定理可得:,
即,
可得,
可得或舍,
即的值为;
由及中,可得,
由正弦定理可得:,
即,解得,而为锐角,
可得;
.
18.解:由题意知,样本中高一学生共有人,其中选择历史学科的学生有人,
故估计高一年级选历史学科的学生有人.
由表格数据可知应从样本中三个年级选历史的学生中分别抽取人数为,,,
编号依次为,,,,,
从这名运动员中随机抽取名参加比赛,所有可能的结果为
,,,,,,,,,,共种,
设为事件“这名参赛同学来自不同年级”,
则
为事件“这名参赛同学来自相同年级”有,共种,所以事件发生的概率
样本中三个年级选第一门科目的学生分别为,,,
所以样本中三个年级选第一门科目的概率分别为,
所以现从高一、高二、高三样本中各随机选取名学生进行调查,
则这名学生均选择了第门科目的概率为.
19.解:证明:因为,所以,
因为平面平面,平面平面,平面,
所以平面,
因为平面,所以,
由三棱柱性质得四边形是平行四边形,又,
所以是菱形,所以,
因为,B、平面,
所以平面,又平面,
所以;
证明:当时,因为,
所以,所以,
由平面,平面,所以,
因为,、平面,
所以平面,又平面,
所以平面平面;
因为平面,平面,
所以直线与平面所成的角为,所以,
因为,且,,,故,
作交于,
因为平面平面,平面平面,平面,
所以平面,又平面,所以,
作交于,连接,
因为,、平面,所以平面,
因为平面,所以,
所以是二面角的平面角,
因为即,所以,
因为即,所以,
所以,
所以二面角的正弦值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若,则( )
A. B. C. D.
2.复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.为了培养青少年无私奉献,服务社会,回馈社会的精神,某学校鼓励学生在假期去社会上的一些福利机构做义工某慈善机构抽查了其中名学生在一年内在福利机构做义工的时间单位:小时,绘制成如图所示的频率分布直方图,则的值为( )
A.
B.
C.
D.
4.若四边形满足:,且,则四边形的形状是( )
A. 矩形 B. 正方形 C. 等腰梯形 D. 菱形
5.抛掷两枚质地均匀的硬币,记事件“第一枚硬币正面朝上”,事件“第二枚硬币反面朝上”,事件“两枚硬币都正面朝上”,事件“至少一枚硬币反面朝上”则( )
A. 与独立 B. 与互斥 C. D.
6.已知内角,,所对边的长分别为,,,,则形状一定是( )
A. 等腰直角三角形 B. 等边三角形 C. 等腰三角形 D. 直角三角形
7.已知两个平面、,在下列条件下,可以判定平面与平面平行的是( )
A. 、都垂直于一个平面
B. 平面内有无数条直线与平面平行
C. 、是内两条直线,且,
D. 、是两条异面直线,且,,,
8.正三棱柱的底面边长为,侧棱长为,为中点,则三棱锥的体积为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知向量,,且,则下列说法正确的是( )
A. B.
C. 向量与夹角是 D.
10.若,,则下列结论正确的有( )
A. B. 若,则
C. 若,则 D. 若,则
11.如图所示,在正方体中,,分别是,的中点,是线段上的动点,则下列判断正确的是( )
A. 三棱锥的体积是定值
B. 过,,三点的平面截正方体所得的截面是六边形
C. 存在唯一的点,使得
D. 与平面所成的角为定值
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,,且,则 ______.
13.甲、乙两人独立解同一道数学题目,甲解出这道题目的概率是,乙解出这道题目的概率是,这道题被解出至少有一人解出来的概率是______.
14.在中,,满足此条件有两解,则边长度的取值范围为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,.
若与垂直,求实数的值;
已知,,,为平面内四点,且,,若,,三点共线,求实数的值.
16.本小题分
如图,在多面体中,四边形是菱形,平面,,,.
求证:平面;
求证:平面.
17.本小题分
在中,,,.
求值;
求角和的面积.
18.本小题分
某地区课改时实行高考新方案试点,规定:语文、数学和英语是必考科目,考生还要从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目为了解某校学生选科情况,现从高一、高二、高三学生中各随机选取了名学生作为样本进行调查,调查数据如下表,用频率估计概率.
选考情况 第门 第门 第门 第门 第门 第门
物理 化学 生物 历史 地理 政治
高一选科人数
高二选科人数
高三选科人数
已知该校高一年级有人,估计该学校高一年级学生中选考历史的人数;
现采用分层抽样的方式从样本中随机抽取三个年级中选择历史学科的名学生组成兴趣小组,再从这人中随机抽取名同学参加知识问答比赛,求这名参赛同学来自不同年级的概率;
假设三个年级选择选考科目是相互独立的为了解不同年级学生对各科目的选择倾向,现从高一、高二、高三样本中各随机选取名学生进行调查,求这名学生均选择了第门科目的概率.
19.本小题分
如图,在三棱柱中,底面中角为直角,,侧面底面.
求证:;
当,直线与平面所成角为时,
求证:平面平面;
求二面角的正弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为,,
所以,
,
因为与垂直,所以,
解得;
因为,
,
所以,
,
因为,,三点共线,所以.
所以,
解得.
16.证明:连接,交于点,
四边形为菱形,,
平面,平面,,
,,平面,
平面;
证明:取的中点,连接,,
又为的中点,则,,
已知,,
则有,,四边形为平行四边形,
有,即有,
平面,平面,
平面.
17.解:因为,
由正弦定理可得:,
在中,可得,,
可得,
又因为,,
由余弦定理可得:,
即,
可得,
可得或舍,
即的值为;
由及中,可得,
由正弦定理可得:,
即,解得,而为锐角,
可得;
.
18.解:由题意知,样本中高一学生共有人,其中选择历史学科的学生有人,
故估计高一年级选历史学科的学生有人.
由表格数据可知应从样本中三个年级选历史的学生中分别抽取人数为,,,
编号依次为,,,,,
从这名运动员中随机抽取名参加比赛,所有可能的结果为
,,,,,,,,,,共种,
设为事件“这名参赛同学来自不同年级”,
则
为事件“这名参赛同学来自相同年级”有,共种,所以事件发生的概率
样本中三个年级选第一门科目的学生分别为,,,
所以样本中三个年级选第一门科目的概率分别为,
所以现从高一、高二、高三样本中各随机选取名学生进行调查,
则这名学生均选择了第门科目的概率为.
19.解:证明:因为,所以,
因为平面平面,平面平面,平面,
所以平面,
因为平面,所以,
由三棱柱性质得四边形是平行四边形,又,
所以是菱形,所以,
因为,B、平面,
所以平面,又平面,
所以;
证明:当时,因为,
所以,所以,
由平面,平面,所以,
因为,、平面,
所以平面,又平面,
所以平面平面;
因为平面,平面,
所以直线与平面所成的角为,所以,
因为,且,,,故,
作交于,
因为平面平面,平面平面,平面,
所以平面,又平面,所以,
作交于,连接,
因为,、平面,所以平面,
因为平面,所以,
所以是二面角的平面角,
因为即,所以,
因为即,所以,
所以,
所以二面角的正弦值为.
第1页,共1页
同课章节目录
