湖南省常德市西洞庭管理区第一中学2024-2025学年高一上学期入学自测数学试题(无答案)
文档属性
| 名称 | 湖南省常德市西洞庭管理区第一中学2024-2025学年高一上学期入学自测数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 316.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 00:00:00 | ||
图片预览


文档简介
2024年秋高一入学自测卷·数学
(120分钟,150分)
第Ⅰ卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列计算正确的是( )
A. B. C. D.
2.由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A.8 B.7 C.6 D.5
3.为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神,某学校积极开设种植类劳动教育课.某班决定每位学生随机抽取一张卡片来确定自己的种植项目,老师提供6张背面完全相同的卡片,其中蔬菜类有4张,正面分别印有白菜、辣椒、豇豆、茄子图案;水果类有2张,正面分别印有草莓、西瓜图案,每个图案对应该种植项目.把这6张卡片背面朝上洗匀,小明随机抽取一张,他恰好抽中水果类卡片的概率是( )
A. B. C. D.
4.“当x<1时,二次函数y=ax2+2x-1随x的增大而增大”的一个充分不必要条件为( ).
A.a>1 B.a<-2
C.-5.一商店在某一时间以每件120元的价格卖出两件衣服,其中一件盈利20%,另一件亏损20%,在这次买卖中,这家商店( )
A.不盈不亏 B.盈利20元
C.亏损10元 D.亏损30元
6.如图,在中,,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论不正确的是( )
A.AD平分 B.
C.点D在AB的垂直平分线上 D.
7.如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形拼出来的图形的总长度是( )
A. B.
C. D.
8.若一组数据,,的平均数为4,方差为3,那么数据,,的平均数和方差分别是( )
A.4,3 B.6,3 C.3,4 D.6,5
9. 甲 乙两人解关于的不等式,甲写错了常数,得到的解集为;乙写错了常数,得到的解集为.那么原不等式的解集为( )
A. B.
C. D.
10.定义:在平面直角坐标系中,对于点,当点满足时,称点是点的“倍增点”,已知点,有下列结论:
①点,都是点的“倍增点”;
②若直线上的点A是点的“倍增点”,则点A的坐标为;
③抛物线上存在两个点是点的“倍增点”;
④若点是点的“倍增点”,则的最小值是.
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
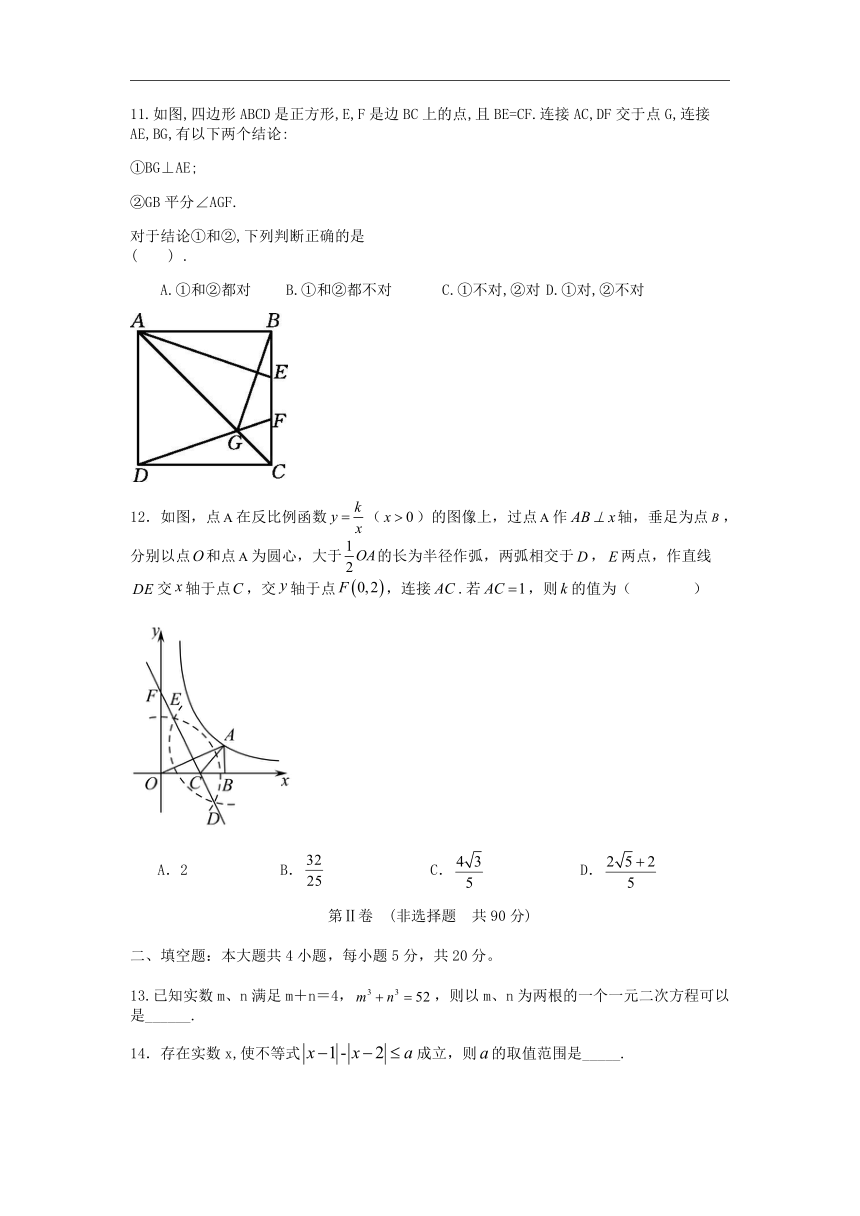
11.如图,四边形ABCD是正方形,E,F是边BC上的点,且BE=CF.连接AC,DF交于点G,连接AE,BG,有以下两个结论:
①BG⊥AE;
②GB平分∠AGF.
对于结论①和②,下列判断正确的是 ( ) .
A.①和②都对 B.①和②都不对 C.①不对,②对 D.①对,②不对
12.如图,点在反比例函数()的图像上,过点作轴,垂足为点,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,作直线交轴于点,交轴于点,连接.若,则的值为( )
A.2 B. C. D.
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分。
13.已知实数m、n满足m+n=4,,则以m、n为两根的一个一元二次方程可以是______.
14.存在实数x,使不等式成立,则的取值范围是_____.
15.如图,正六边形的边长为2,以为圆心,的长为半径画弧,得弧,连结,,则图中阴影部分的面积为 .
16.小明对自己上学路线的长度进行了20次测量,得到20个数据x1,x2,…,x20,已知x1+x2+…+x20=2024,当代数式(x-x1)2+(x-x2)2+…+(x-x20)2取得最小值时,x的值为 .
三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.本小题满分10分.
化简y=+,并画出简图,写出最小值.
18.本小题满分12分.
已知集合A=,B={x|a≤x<2a+1,a∈R}.
(1)求A;(6分)
(2)若B A,求实数a的取值范围.(6分)
19.本小题满分12分
如图,以边长为4的正方形ABCD的中心为原点,构建一个平面直角坐标系.现做如下实验:连续抛掷一枚质地均匀的正方体的骰子(六个面分别标有1至6这六个点数中的一个)两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数作为横坐标,第二次的点数作为纵坐标).
(1)①请用画树状图或列表的方法,表示出点P的坐标的所有可能的结果; (4分)
②求点P在正方形ABCD中(含正方形内部和边界)的概率. (4分)
(2)试将正方形ABCD平移整数个单位长度,则是否存在一种平移,使点P在正方形ABCD中的概率为 若存在,请写出平移方式;若不存在,请说明理由. (4分)
20.本小题满分12分
为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有两种型号的挖掘机,已知3台型和5台型挖掘机同时施工一小时挖土165立方米;4台型和7台型挖掘机同时施工一小时挖土225立方米.每台型挖掘机一小时的施工费用为300元,每台型挖掘机一小时的施工费用为180元.
(1)分别求每台型,型挖掘机一小时挖土多少立方米?(6分)
(2)若不同数量的型和型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?(6分)
21.本小题满分12分
如图1,抛物线交轴于点,交轴于点.
(1)求和的值;(4分)
(2)已知点,是抛物线上的两个点,且,,求此抛物线的顶点到的距离;(4分)
(3)如图2,连接,点是抛物线在线段上方部分上的一个动点,连接,交线段于点,设,求的取值范围. (4分)
22.本小题满分12分
如图1,点A,B,D,C在同一条直线上,B是AC的中点,点D在线段BC上,BC=4,CD=3,DE⊥AC于点D,DE=4,以AB为直径,在直线AC的上方作半圆O.
(1)求点O到CE的距离. (4分)
(2)如图2,将半圆O与直径AB绕点B顺时针旋转α(0°<α<180°)得到半圆O'与直径A'B(点A'为点A的对应点).
①当半圆O'与DE相切,切点记为P时,求扇形A'O'P的面积; (4分)
②当点A'恰好落△CDE的边上时,直接写出tan∠A'BD的值. (4分)
(120分钟,150分)
第Ⅰ卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列计算正确的是( )
A. B. C. D.
2.由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A.8 B.7 C.6 D.5
3.为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神,某学校积极开设种植类劳动教育课.某班决定每位学生随机抽取一张卡片来确定自己的种植项目,老师提供6张背面完全相同的卡片,其中蔬菜类有4张,正面分别印有白菜、辣椒、豇豆、茄子图案;水果类有2张,正面分别印有草莓、西瓜图案,每个图案对应该种植项目.把这6张卡片背面朝上洗匀,小明随机抽取一张,他恰好抽中水果类卡片的概率是( )
A. B. C. D.
4.“当x<1时,二次函数y=ax2+2x-1随x的增大而增大”的一个充分不必要条件为( ).
A.a>1 B.a<-2
C.-
A.不盈不亏 B.盈利20元
C.亏损10元 D.亏损30元
6.如图,在中,,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论不正确的是( )
A.AD平分 B.
C.点D在AB的垂直平分线上 D.
7.如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形拼出来的图形的总长度是( )
A. B.
C. D.
8.若一组数据,,的平均数为4,方差为3,那么数据,,的平均数和方差分别是( )
A.4,3 B.6,3 C.3,4 D.6,5
9. 甲 乙两人解关于的不等式,甲写错了常数,得到的解集为;乙写错了常数,得到的解集为.那么原不等式的解集为( )
A. B.
C. D.
10.定义:在平面直角坐标系中,对于点,当点满足时,称点是点的“倍增点”,已知点,有下列结论:
①点,都是点的“倍增点”;
②若直线上的点A是点的“倍增点”,则点A的坐标为;
③抛物线上存在两个点是点的“倍增点”;
④若点是点的“倍增点”,则的最小值是.
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
11.如图,四边形ABCD是正方形,E,F是边BC上的点,且BE=CF.连接AC,DF交于点G,连接AE,BG,有以下两个结论:
①BG⊥AE;
②GB平分∠AGF.
对于结论①和②,下列判断正确的是 ( ) .
A.①和②都对 B.①和②都不对 C.①不对,②对 D.①对,②不对
12.如图,点在反比例函数()的图像上,过点作轴,垂足为点,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,作直线交轴于点,交轴于点,连接.若,则的值为( )
A.2 B. C. D.
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分。
13.已知实数m、n满足m+n=4,,则以m、n为两根的一个一元二次方程可以是______.
14.存在实数x,使不等式成立,则的取值范围是_____.
15.如图,正六边形的边长为2,以为圆心,的长为半径画弧,得弧,连结,,则图中阴影部分的面积为 .
16.小明对自己上学路线的长度进行了20次测量,得到20个数据x1,x2,…,x20,已知x1+x2+…+x20=2024,当代数式(x-x1)2+(x-x2)2+…+(x-x20)2取得最小值时,x的值为 .
三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.本小题满分10分.
化简y=+,并画出简图,写出最小值.
18.本小题满分12分.
已知集合A=,B={x|a≤x<2a+1,a∈R}.
(1)求A;(6分)
(2)若B A,求实数a的取值范围.(6分)
19.本小题满分12分
如图,以边长为4的正方形ABCD的中心为原点,构建一个平面直角坐标系.现做如下实验:连续抛掷一枚质地均匀的正方体的骰子(六个面分别标有1至6这六个点数中的一个)两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数作为横坐标,第二次的点数作为纵坐标).
(1)①请用画树状图或列表的方法,表示出点P的坐标的所有可能的结果; (4分)
②求点P在正方形ABCD中(含正方形内部和边界)的概率. (4分)
(2)试将正方形ABCD平移整数个单位长度,则是否存在一种平移,使点P在正方形ABCD中的概率为 若存在,请写出平移方式;若不存在,请说明理由. (4分)
20.本小题满分12分
为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有两种型号的挖掘机,已知3台型和5台型挖掘机同时施工一小时挖土165立方米;4台型和7台型挖掘机同时施工一小时挖土225立方米.每台型挖掘机一小时的施工费用为300元,每台型挖掘机一小时的施工费用为180元.
(1)分别求每台型,型挖掘机一小时挖土多少立方米?(6分)
(2)若不同数量的型和型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?(6分)
21.本小题满分12分
如图1,抛物线交轴于点,交轴于点.
(1)求和的值;(4分)
(2)已知点,是抛物线上的两个点,且,,求此抛物线的顶点到的距离;(4分)
(3)如图2,连接,点是抛物线在线段上方部分上的一个动点,连接,交线段于点,设,求的取值范围. (4分)
22.本小题满分12分
如图1,点A,B,D,C在同一条直线上,B是AC的中点,点D在线段BC上,BC=4,CD=3,DE⊥AC于点D,DE=4,以AB为直径,在直线AC的上方作半圆O.
(1)求点O到CE的距离. (4分)
(2)如图2,将半圆O与直径AB绕点B顺时针旋转α(0°<α<180°)得到半圆O'与直径A'B(点A'为点A的对应点).
①当半圆O'与DE相切,切点记为P时,求扇形A'O'P的面积; (4分)
②当点A'恰好落△CDE的边上时,直接写出tan∠A'BD的值. (4分)
同课章节目录
