高中数学必修一第三章 函数概念与性质 单元测试(含解析)
文档属性
| 名称 | 高中数学必修一第三章 函数概念与性质 单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 148.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 07:04:10 | ||
图片预览




文档简介
高中数学必修一第三章
一、单选题
1.函数f(x)= 的定义域为( )
A.[-1,2)∪(2,+∞) B.(-1,+∞)
C.[-1,2) D.[-1,+∞)
2.某工厂今年前五个月每月生产某种产品的数量C(件)关于时间t(月)的函数图象如图所示,则这个工厂对这种产品来说( )
A.一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少
B.一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平
C.一至三月每月生产数量逐月增加,四、五两月均停止生产
D.一至三月每月生产数量不变,四、五两月均停止生产
3.设全集为R,函数 的定义域为M,则 =( )
A. B.
C. D.
4.狄利克雷函数是数学中非常有名且很重要的一个函数.它的定义如下: ,则关于狄利克雷函数 的说法错误的一项是( )
A.定义域为R
B.值域为
C.是偶函数
D.对定义域内任意 都有
5.函数f (x )= 的奇偶性及单调性的情况是( )
A.增函数、偶函数 B.减函数、奇函数
C.增函数、非奇非偶函数 D.减函数、非奇非偶函数
6.已知 ,则 ( )
A. B. C. D.
7.定义在上的函数满足,,,且当时,,则( )
A. B. C. D.
8.已知定义在R上的单调递增的函数满足:任意,有,,则下列结论错误的是( )
A.当时,
B.任意
C.存在非零实数,使得任意
D.存在非零实数,使得任意
二、多选题
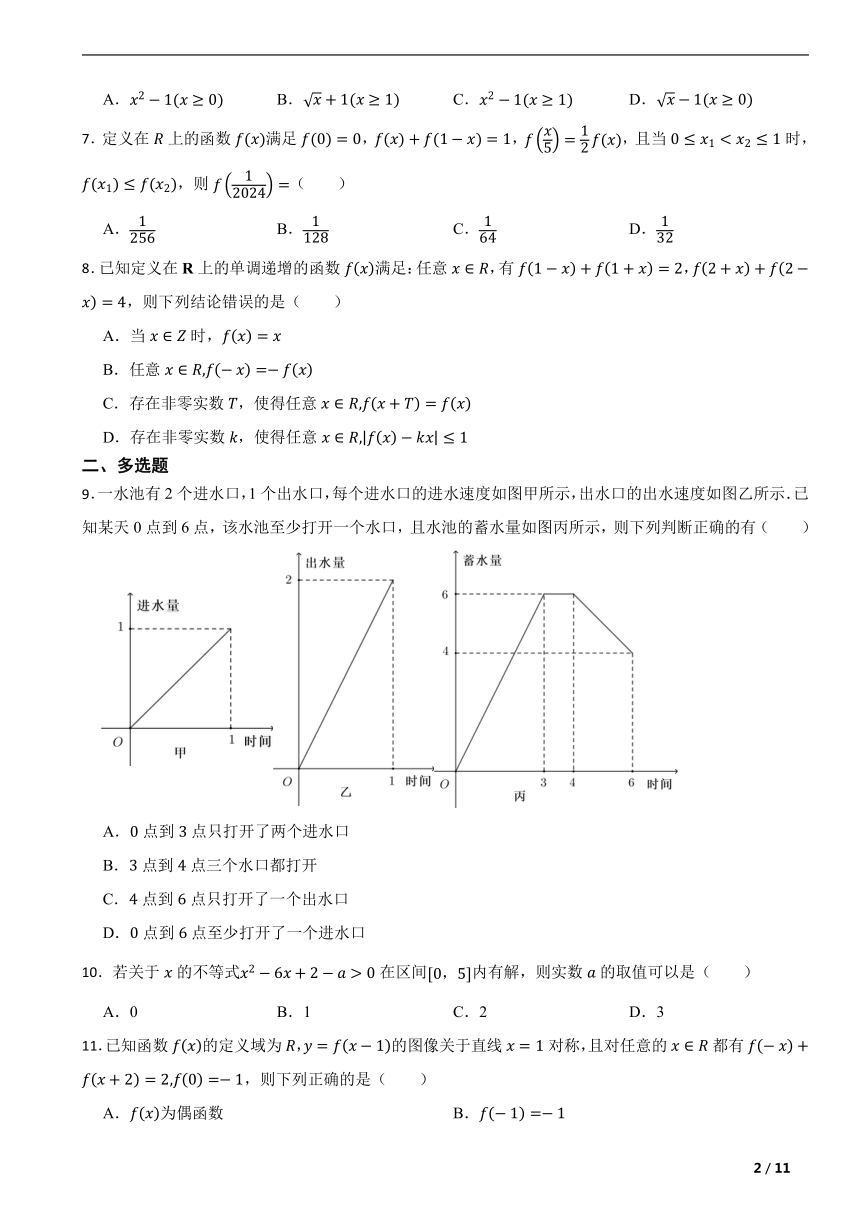
9.一水池有2个进水口,1个出水口,每个进水口的进水速度如图甲所示,出水口的出水速度如图乙所示.已知某天0点到6点,该水池至少打开一个水口,且水池的蓄水量如图丙所示,则下列判断正确的有( )
A.点到点只打开了两个进水口
B.点到点三个水口都打开
C.点到点只打开了一个出水口
D.点到点至少打开了一个进水口
10.若关于的不等式在区间内有解,则实数的取值可以是( )
A.0 B.1 C.2 D.3
11.已知函数的定义域为,的图像关于直线对称,且对任意的都有,则下列正确的是( )
A.为偶函数 B.
C.2是的一个周期 D.
12.已知函数,对任意的实数x,y都有成立,,,则( )
A.为偶函数 B.
C. D.4为的一个周期
三、填空题
13.已知是一次函数,且,则 .
14.已知定义在 上的奇函数 ,当 时, ,则 .
15.已知奇函数f(x)是定义在(﹣3,3)上的减函数,且满足不等式f(x﹣3)+f(x2﹣3)<0,则不等式解集 .
16.已知函数,若对,使得,则实数的取值范围为 .
四、解答题
17.已知是定义在上的奇函数,当时,,且.
(1)求的解析式;
(2)画出的图象,并根据图象写出的单调区间(直接写出,无需证明).
18.定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y ,有 , .
(1)求 的值;
(2)求证:对任意x ,都有f(x)>0;
(3)解不等式f(3 2x)>4.
19.已知函数f(x)=|x|+ ﹣1(x≠0)
(1)当m=1时,判断f(x)在(﹣∞,0)的单调性,并用定义证明;
(2)讨论f(x)零点的个数.
20.已知二次函数.
(1)若函数满足,且.求的解析式;
(2)若对任意,不等式恒成立,求的最大值.
21.在数学探究活动中,某兴趣小组合作制作一个工艺品,设计了如图所示的一个窗户,其中矩形的三边,,由长为8厘米的材料弯折而成,边的长为厘米();曲线是一段抛物线,在如图所示的平面直角坐标系中,其解析式为,记窗户的高(点到边的距离)为.
(1)求函数的解析式;
(2)要使得窗户的高最小,边应设计成多少厘米?
(3)要使得窗户的高与长的比值达到最小,边应设计成多少厘米?
22.对于定义域为 的函数 ,若同时满足下列两个条件:① 在 上具有单调性;②存在区间 ,使 在区间 上的值域也为 ,则称 为 上的“精彩函数”,区间 为函数 的“精彩区间”.
(1)判断 是否为函数 的“精彩区间”,并说明理由;
(2)判断函数 是否为“精彩函数”,并说明理由;
(3)若函数 是“精彩函数”,求实数 的取值范围.
参考答案
1.A
要使函数有意义,
则 ,
解得 且 ,
所以函数的定义域为[-1,2)∪(2,+∞),
2.B
解:∵所给图象表示的是前五个月每月生产某种产品的数量C(件)关于时间t(月)的函数图象,
从图象上看一至三月份的产品数量逐月增加,从三月份开始产量稳定,
四月份、五月份的产量和三月份的产量持平.
∴一至三月每月生产数量逐月增加,四、五月生产数量与三月持平.
3.C
由 ,解得 且 ,故其补集为 或 .
4.B
则函数定义域为R,A符合题意;值域为 B不符合题意;
,是偶函数,C符合题意;
,D符合题意.
5. C
解答:由题可知: 则可得函数定义域为:﹣1≤x<1,所以为非奇非偶函数.
令g(x)= =﹣ =﹣(1+ ),
由此判断g(x)在﹣1≤x<1上单调递增,从而知f(x)在﹣1≤x<1上也单调递增.
6.C
令 , ,则 ,
由 得, , ,
即 , 。
7. D
解:,,
令得:,又,
反复利用可得:
①,
再令,由,可求得,
同理反复利用可得:
②,
由①②可得:有,
,,而,
所以,,
故.
8. C
9. A,B,D
由甲、乙图知:每个进水口进水速度为,每个出水口出水速度为2,
对于A:由丙图知:点到点蓄水量增加,所以只打开了两个进水口,只进水不出水,A符合题意;
对于B:点到点蓄水量不变,说明三个水口都打开进出一样多蓄水量不变,B符合题意;
对于C:点到点蓄水量减少,说明每个小时减少,所以打开了一个进水口和一个出水口,C不正确;
对于D:由ABC的分析可知,点到点至少打开了一个进水口,D符合题意;
10. A,B
解:,在区间内有解,在区间内有解,
令,则,的对称轴是是最大值,
.又因为,所以只能取0,1.
11.A,D
解:对于A,因为函数的定义域为,的图像关于直线对称,
所以关于轴对称,即,所以为偶函数,故A正确;
对于B,因为,
令,可得,则,
因为为偶函数,所以,故B不正确;
对于C,由,
令,可得:,,2是不是的一个周期,故C不正确;
对于D,因为,,所以,
所以,则,即是以4为周期的周期函数,
所以,故D正确.
故答案为:AD.
12. B,C,D
13.
设,
因为,
则,
可知,解得,故.
14.-1
因为定义在 上的奇函数 ,当 时, ,
所以 ,所以 ,
15.(2, )
解:因为f(x)是奇函数,所以不等式f(x﹣3)+f(x2﹣3)<0等价为f(x2﹣3)<﹣f(x﹣3)=f(3﹣x),
又f(x)是定义在(﹣3,3)上的减函数,
所以 ,即 ,解得2 ,
即不等式的解集为(2, ).
16.
因为对,,使得,则,
,在上单调递增,所以,
令,则,在上单调递减,上单调递增,所以当时取得最小值,,
所以,解得。
17.(1)解:是定义在上的奇函数,所以,,
解得.
所以当时,,
当时,,.
所以
(2)解:的图象如下:
由图可知,的单调增区间为和,单调减区间为.
18.(1)解:对任意x,y , .
令x=y=0,得f(0)=f(0)·f(0),即f(0)·[f(0) 1]=0.
令y=0,得f(x)=f(x)·f(0),对任意x 成立,
所以f(0)≠0,因此f(0)=1
(2)证明:对任意x ,有 .
假设存在x0 ,使f(x0)=0,
则对任意x>0,有f(x)=f[(x x0)+x0]=f(x x0)·f(x0)=0.
这与已知x>0时,f(x)>1矛盾.所以,对任意x ,均有f(x)>0成立.
(3)解:令x=y=1有f(1 1)=f(1)·f(1),
所以f(2)=22=4.任取x1,x2 ,且x1则f(x2)-f(x1)=f[(x2 x1)+x1] f(x1)=f(x2 x1)·f(x1) f(x1)=f(x1)·[f(x2 x1) 1].
∵x10,由已知f(x2 x1)>1,∴f(x2 x1) 1>0.
由(2)知x1 ,f(x1)>0.所以f(x2) f(x1)>0,即f(x1)故函数f(x)在 上是增函数.
由f(3 2x)>4,得f(3 2x)>f(2),即3 2x>2.解得x< .所以,不等式的解集是 .
19.(1)解:由当m=1,且x<0时,f(x)=﹣x+ ﹣1是单调递减的.
证明:设x1<x2<0,则
f(x1)﹣f(x2)=﹣x1+ ﹣1﹣(﹣x2+ ﹣1)=x2﹣x1+ ﹣
=(x2﹣x1)﹣ =(x2﹣x1)(1+ ),
∵x1<x2<0,则x2﹣x1>0,x1x2>0,则有f(x1)﹣f(x2)>0,
f(x1)>f(x2)
则f(x)在(﹣∞,0)上为减函数
(2)解:由f(x)=0可得x|x|﹣x+m=0,变为m=﹣x|x|+x,x≠0
令h(x)=x﹣x|x|=
作出函数h(x)的图象及直线y=m,由图象可得:
当m> 或m<﹣ 时,f(x)有1个零点.
当m= 或m=0或m=﹣ 时,f(x)有2个零点;
当0<m< 或﹣ <m<0时,f(x)有3个零点.
20.(1)解:设,
由已知代入,
得,
对于恒成立,
故,解得,又由,得,
所以
(2)解:若对任意,不等式恒成立,
整理得:恒成立,因为a不为0,
所以,所以,
所以,
令,因为,所以,
若时,此时,
若时,,
当时,即时,上式取得等号,
综上的最大值为.
21.(1)因为抛物线方程为,所以
又因为,所以点到的距离为
所以点到的距离为,即
(2)因为,所以当时有最小值
此时,,故应设计为3厘米
(3)窗户的高与长的比值为
因为,当且仅当,即时取等号
所以要使得窗户的高与长的比值达到最小,厘米
22.(1)解:由题意, 是 上的增函数,
易知 在 上的值域为 ,
所以函数 是“精彩区间”, 是该函数的“精彩区间”.
(2)解:不是精彩函数,证明如下:
因为函数 在区间 上单调递减,在区间 上单调递增,
所以函数 在定义域 上不单调,不满足“精彩函数”的第一个条件,
所以函数 不是“精彩函数”.
(3)解:由题意,函数 的定义域为 ,且 在定义域上为单调递增函数,
因为函数 是“精彩函数”,所以方程 至少存在两个不等的实数解,
方程整理得 ,
所以该方程有两个不等的实数根,设为 ,不妨设 ,则 , ,
令 ,
由题意得, ,
即 ,解得 .
所以实数 的取值范围是 .
1 / 1
一、单选题
1.函数f(x)= 的定义域为( )
A.[-1,2)∪(2,+∞) B.(-1,+∞)
C.[-1,2) D.[-1,+∞)
2.某工厂今年前五个月每月生产某种产品的数量C(件)关于时间t(月)的函数图象如图所示,则这个工厂对这种产品来说( )
A.一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少
B.一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平
C.一至三月每月生产数量逐月增加,四、五两月均停止生产
D.一至三月每月生产数量不变,四、五两月均停止生产
3.设全集为R,函数 的定义域为M,则 =( )
A. B.
C. D.
4.狄利克雷函数是数学中非常有名且很重要的一个函数.它的定义如下: ,则关于狄利克雷函数 的说法错误的一项是( )
A.定义域为R
B.值域为
C.是偶函数
D.对定义域内任意 都有
5.函数f (x )= 的奇偶性及单调性的情况是( )
A.增函数、偶函数 B.减函数、奇函数
C.增函数、非奇非偶函数 D.减函数、非奇非偶函数
6.已知 ,则 ( )
A. B. C. D.
7.定义在上的函数满足,,,且当时,,则( )
A. B. C. D.
8.已知定义在R上的单调递增的函数满足:任意,有,,则下列结论错误的是( )
A.当时,
B.任意
C.存在非零实数,使得任意
D.存在非零实数,使得任意
二、多选题
9.一水池有2个进水口,1个出水口,每个进水口的进水速度如图甲所示,出水口的出水速度如图乙所示.已知某天0点到6点,该水池至少打开一个水口,且水池的蓄水量如图丙所示,则下列判断正确的有( )
A.点到点只打开了两个进水口
B.点到点三个水口都打开
C.点到点只打开了一个出水口
D.点到点至少打开了一个进水口
10.若关于的不等式在区间内有解,则实数的取值可以是( )
A.0 B.1 C.2 D.3
11.已知函数的定义域为,的图像关于直线对称,且对任意的都有,则下列正确的是( )
A.为偶函数 B.
C.2是的一个周期 D.
12.已知函数,对任意的实数x,y都有成立,,,则( )
A.为偶函数 B.
C. D.4为的一个周期
三、填空题
13.已知是一次函数,且,则 .
14.已知定义在 上的奇函数 ,当 时, ,则 .
15.已知奇函数f(x)是定义在(﹣3,3)上的减函数,且满足不等式f(x﹣3)+f(x2﹣3)<0,则不等式解集 .
16.已知函数,若对,使得,则实数的取值范围为 .
四、解答题
17.已知是定义在上的奇函数,当时,,且.
(1)求的解析式;
(2)画出的图象,并根据图象写出的单调区间(直接写出,无需证明).
18.定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y ,有 , .
(1)求 的值;
(2)求证:对任意x ,都有f(x)>0;
(3)解不等式f(3 2x)>4.
19.已知函数f(x)=|x|+ ﹣1(x≠0)
(1)当m=1时,判断f(x)在(﹣∞,0)的单调性,并用定义证明;
(2)讨论f(x)零点的个数.
20.已知二次函数.
(1)若函数满足,且.求的解析式;
(2)若对任意,不等式恒成立,求的最大值.
21.在数学探究活动中,某兴趣小组合作制作一个工艺品,设计了如图所示的一个窗户,其中矩形的三边,,由长为8厘米的材料弯折而成,边的长为厘米();曲线是一段抛物线,在如图所示的平面直角坐标系中,其解析式为,记窗户的高(点到边的距离)为.
(1)求函数的解析式;
(2)要使得窗户的高最小,边应设计成多少厘米?
(3)要使得窗户的高与长的比值达到最小,边应设计成多少厘米?
22.对于定义域为 的函数 ,若同时满足下列两个条件:① 在 上具有单调性;②存在区间 ,使 在区间 上的值域也为 ,则称 为 上的“精彩函数”,区间 为函数 的“精彩区间”.
(1)判断 是否为函数 的“精彩区间”,并说明理由;
(2)判断函数 是否为“精彩函数”,并说明理由;
(3)若函数 是“精彩函数”,求实数 的取值范围.
参考答案
1.A
要使函数有意义,
则 ,
解得 且 ,
所以函数的定义域为[-1,2)∪(2,+∞),
2.B
解:∵所给图象表示的是前五个月每月生产某种产品的数量C(件)关于时间t(月)的函数图象,
从图象上看一至三月份的产品数量逐月增加,从三月份开始产量稳定,
四月份、五月份的产量和三月份的产量持平.
∴一至三月每月生产数量逐月增加,四、五月生产数量与三月持平.
3.C
由 ,解得 且 ,故其补集为 或 .
4.B
则函数定义域为R,A符合题意;值域为 B不符合题意;
,是偶函数,C符合题意;
,D符合题意.
5. C
解答:由题可知: 则可得函数定义域为:﹣1≤x<1,所以为非奇非偶函数.
令g(x)= =﹣ =﹣(1+ ),
由此判断g(x)在﹣1≤x<1上单调递增,从而知f(x)在﹣1≤x<1上也单调递增.
6.C
令 , ,则 ,
由 得, , ,
即 , 。
7. D
解:,,
令得:,又,
反复利用可得:
①,
再令,由,可求得,
同理反复利用可得:
②,
由①②可得:有,
,,而,
所以,,
故.
8. C
9. A,B,D
由甲、乙图知:每个进水口进水速度为,每个出水口出水速度为2,
对于A:由丙图知:点到点蓄水量增加,所以只打开了两个进水口,只进水不出水,A符合题意;
对于B:点到点蓄水量不变,说明三个水口都打开进出一样多蓄水量不变,B符合题意;
对于C:点到点蓄水量减少,说明每个小时减少,所以打开了一个进水口和一个出水口,C不正确;
对于D:由ABC的分析可知,点到点至少打开了一个进水口,D符合题意;
10. A,B
解:,在区间内有解,在区间内有解,
令,则,的对称轴是是最大值,
.又因为,所以只能取0,1.
11.A,D
解:对于A,因为函数的定义域为,的图像关于直线对称,
所以关于轴对称,即,所以为偶函数,故A正确;
对于B,因为,
令,可得,则,
因为为偶函数,所以,故B不正确;
对于C,由,
令,可得:,,2是不是的一个周期,故C不正确;
对于D,因为,,所以,
所以,则,即是以4为周期的周期函数,
所以,故D正确.
故答案为:AD.
12. B,C,D
13.
设,
因为,
则,
可知,解得,故.
14.-1
因为定义在 上的奇函数 ,当 时, ,
所以 ,所以 ,
15.(2, )
解:因为f(x)是奇函数,所以不等式f(x﹣3)+f(x2﹣3)<0等价为f(x2﹣3)<﹣f(x﹣3)=f(3﹣x),
又f(x)是定义在(﹣3,3)上的减函数,
所以 ,即 ,解得2 ,
即不等式的解集为(2, ).
16.
因为对,,使得,则,
,在上单调递增,所以,
令,则,在上单调递减,上单调递增,所以当时取得最小值,,
所以,解得。
17.(1)解:是定义在上的奇函数,所以,,
解得.
所以当时,,
当时,,.
所以
(2)解:的图象如下:
由图可知,的单调增区间为和,单调减区间为.
18.(1)解:对任意x,y , .
令x=y=0,得f(0)=f(0)·f(0),即f(0)·[f(0) 1]=0.
令y=0,得f(x)=f(x)·f(0),对任意x 成立,
所以f(0)≠0,因此f(0)=1
(2)证明:对任意x ,有 .
假设存在x0 ,使f(x0)=0,
则对任意x>0,有f(x)=f[(x x0)+x0]=f(x x0)·f(x0)=0.
这与已知x>0时,f(x)>1矛盾.所以,对任意x ,均有f(x)>0成立.
(3)解:令x=y=1有f(1 1)=f(1)·f(1),
所以f(2)=22=4.任取x1,x2 ,且x1
∵x1
由(2)知x1 ,f(x1)>0.所以f(x2) f(x1)>0,即f(x1)
由f(3 2x)>4,得f(3 2x)>f(2),即3 2x>2.解得x< .所以,不等式的解集是 .
19.(1)解:由当m=1,且x<0时,f(x)=﹣x+ ﹣1是单调递减的.
证明:设x1<x2<0,则
f(x1)﹣f(x2)=﹣x1+ ﹣1﹣(﹣x2+ ﹣1)=x2﹣x1+ ﹣
=(x2﹣x1)﹣ =(x2﹣x1)(1+ ),
∵x1<x2<0,则x2﹣x1>0,x1x2>0,则有f(x1)﹣f(x2)>0,
f(x1)>f(x2)
则f(x)在(﹣∞,0)上为减函数
(2)解:由f(x)=0可得x|x|﹣x+m=0,变为m=﹣x|x|+x,x≠0
令h(x)=x﹣x|x|=
作出函数h(x)的图象及直线y=m,由图象可得:
当m> 或m<﹣ 时,f(x)有1个零点.
当m= 或m=0或m=﹣ 时,f(x)有2个零点;
当0<m< 或﹣ <m<0时,f(x)有3个零点.
20.(1)解:设,
由已知代入,
得,
对于恒成立,
故,解得,又由,得,
所以
(2)解:若对任意,不等式恒成立,
整理得:恒成立,因为a不为0,
所以,所以,
所以,
令,因为,所以,
若时,此时,
若时,,
当时,即时,上式取得等号,
综上的最大值为.
21.(1)因为抛物线方程为,所以
又因为,所以点到的距离为
所以点到的距离为,即
(2)因为,所以当时有最小值
此时,,故应设计为3厘米
(3)窗户的高与长的比值为
因为,当且仅当,即时取等号
所以要使得窗户的高与长的比值达到最小,厘米
22.(1)解:由题意, 是 上的增函数,
易知 在 上的值域为 ,
所以函数 是“精彩区间”, 是该函数的“精彩区间”.
(2)解:不是精彩函数,证明如下:
因为函数 在区间 上单调递减,在区间 上单调递增,
所以函数 在定义域 上不单调,不满足“精彩函数”的第一个条件,
所以函数 不是“精彩函数”.
(3)解:由题意,函数 的定义域为 ,且 在定义域上为单调递增函数,
因为函数 是“精彩函数”,所以方程 至少存在两个不等的实数解,
方程整理得 ,
所以该方程有两个不等的实数根,设为 ,不妨设 ,则 , ,
令 ,
由题意得, ,
即 ,解得 .
所以实数 的取值范围是 .
1 / 1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
