人教版数学八上 第十二章 全等三角形 单元练习(含答案)
文档属性
| 名称 | 人教版数学八上 第十二章 全等三角形 单元练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 836.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 00:00:00 | ||
图片预览




文档简介
人教版数学八上第十二章
一、单选题
1.下列说法正确的是( )
A.两个直角三角形一定全等 B.形状相同的两个三角形全等
C.全等三角形的面积一定相等 D.面积相等的两个三角形全等
2.如图,在四边形ABCD中,AB=AD,CB=CD,点E在AC上,则图中全等三角形共有
A.1对 B.2对 C.3对 D.4对
3.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠AOB=∠A′O′B′,需要证明△COD和△C'O'D',则这两个三角形全等的依据是( )
A.SAS B.AAS C.SSS D.ASA
4.如图,中,,平分交于,过点作交于,下列结论中错误的是( )
A. B. C. D.
5.以下判断两个直角三角形全等的各种条件:(1)一个锐角和一边对应相等;(2)两对对应直角边相等;(3)两对锐角对应相等,其中能得到两个直角三角形全等的条件有( )
A.0个 B.1个 C.2个 D.3个
6.如图,AD是 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则EF=( ).
A.2.5 B.2 C.1.5 D.1
7.如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=18,DE=3,AB=7,则AC长是( )
A.5 B.6 C.4 D.7
8.如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
9.三角形是一种常见且神奇的图形,我们小学阶段就知道,三角形的内角和等于180°.如图,△ABC的角平分线BE、CD相交于点F,∠A=90°,GD//BC,BG⊥GD于点G,下列结论:①∠CBG=90°;②∠BDG=2∠ABE;③∠BFD=∠FBC+∠FCB;④∠AEB=∠EBG;⑤∠CFE=45°,其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
10.如图,在中,.分别为上的动点,且,连接,则的最小值为( )
A. B. C.6 D.
二、填空题
11. ≌ , , ,若 的周长为偶数,则 .
12.如图,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线是的平分线,由做法得到三角形全等的判定方法是 .
13.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为 .
14.如图,在中,,D,E分别是,上的点.若,则 .
15.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
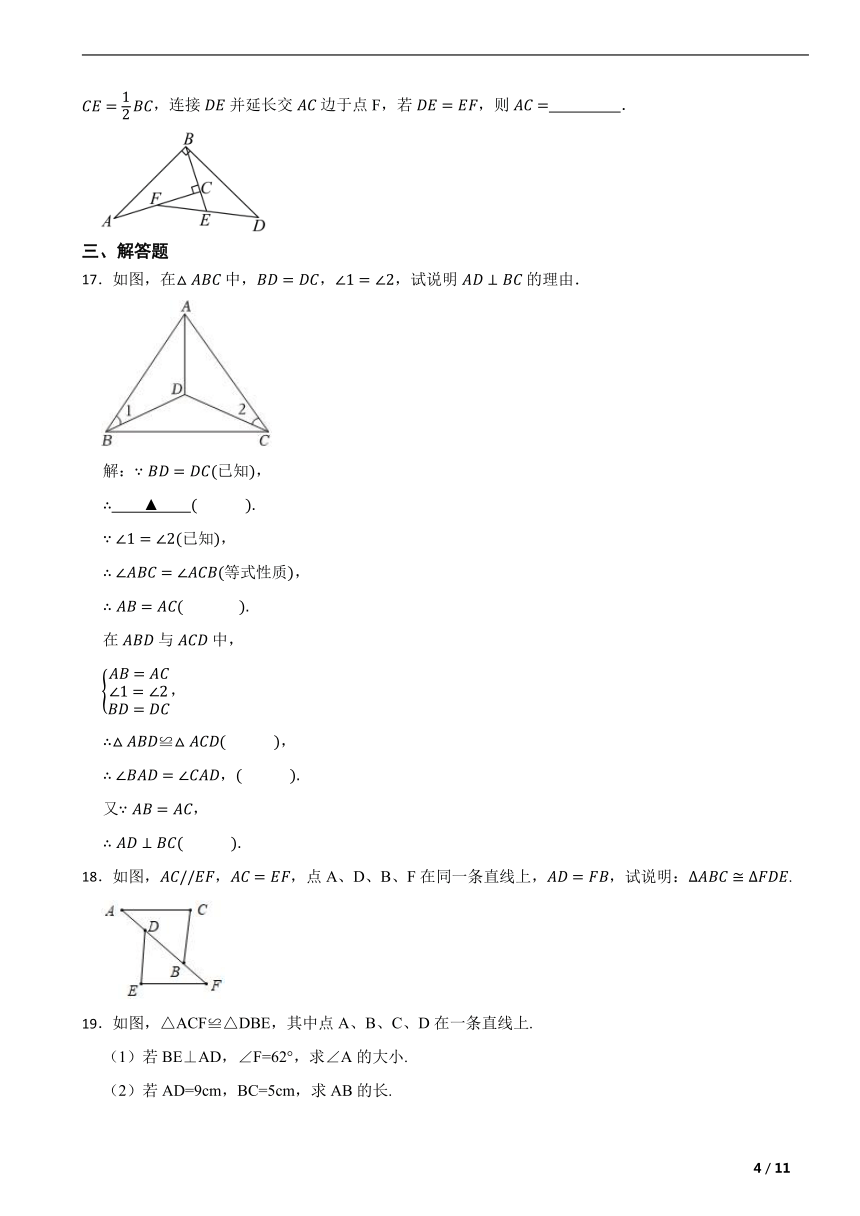
16.如图,在中,,,过点B作,且,延长至点E,使,连接并延长交边于点F,若,则 .
三、解答题
17.如图,在中,,,试说明的理由.
解:已知,
▲
已知,
等式性质,
在与中,
,
≌ ,
,
又,
18.如图,,,点A、D、B、F在同一条直线上,,试说明:.
19.如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
20.如图,是的高,是的角平分线,F是中点,,.
(1)求的度数;
(2)若与的周长差为3,,则_____.
21.在中,平分交于点,点是射线上的动点(不与点重合),过点作交直线于点,的角平分线所在的直线与直线交于点(不与点重合.
(1)如图,点在线段上运动,若,,求的度数;
(2)若点在线段的延长线上时,设,求的度数(答案可用含的代数式表示).
22.阅读理解:如图①,在四边形ABCD中,ABDC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
(1)AB,AD,DC之间的等量关系为
(2)问题探究:如图②,在四边形ABCD中,ABDC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
23.已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,∠BDA=∠AEC=∠BAC
图① 图② 图③
(1)如图①,若AB⊥AC,则BD与AE的数量关系为 ,BD,CE与DE的数量关系为 ;
(2)如图②,当AB不垂直于AC时,(1)中的结论是否成立?请说明理由.
(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,DE=10cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t与x的值;若不存在,请说明理由.
答案解析部分
1.C
2.C
3.C
4.D
5.B
6.C
解:如图,延长AD,使DG=AD,连接BG,
∵AD是△ABC的中线,
∴BD=CD,且DG=AD,∠ADC=∠BDG,
∴△ADC≌△GDB(SAS),
∴AC=DG=CF+AF=6+AF,∠DAC=∠G,
∵EF=AF,
∴∠DAC=∠AEF,
∴∠G=∠AEF=∠BEG,
∴BE=BG=7.5,
∴6+AF=BG=7.5,
∴AF=1.5=EF,
故选择:C.
7.A
8.A
9.A
10.B
11.4
12.SSS
13.4
14.
15.15
16.12
解:如图,过点D作DG⊥BE交BE的延长线于点G,
∵BD⊥AB,
∴∠ABC+∠DBG=90°,
∵∠BDG+∠DBG=90°,
∴∠ABC=∠BDG,
在△ABC和△BDG中,
,
∴△ABC≌△BDG(AAS)
∴AC=BG
在△ECF和△EGD中,
,
∴△ECF≌△EGD(AAS)
∴EG=CE=BC=3,
∴AC=BG=BC+CE+EG=6+3+3=12.
17.解:(已知),
(等边对等角),
(已知),
(等式性质),
(等角对等边),
在ABD与ACD中,
,(全等三角形的对应角相等),
又,
(等腰三角形的三线合一).
18.证明:,
,
,
,
即,
在和中
,
.
19.(1)∠A=28°;(2)AB =2 cm.
20.(1);
(2).
21.(1)
(2)
22.(1)AD=AB+DC
证明:如图①,延长AE交DC的延长线于点F,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠F,
在△AEB和△FEC中,,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAF的平分线,
∴∠BAF=∠DAF,
∵AB∥CD,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
∴DF=AD=DC+CF=AB+DC;
(2)解:AB=AF+CF,证明:如下图,延长AE交DF的延长线于点G,∵E是BC的中点,∴CE=BE,∵AB∥DC,∴∠BAE=∠G,在△AEB和△GEC中,,∴△AEB≌△GEC,∴AB=GC,∵AE是∠BAF的平分线,∴∠BAG=∠FAG,∵AB∥CD,∴∠BAG=∠G,∴∠FAG=∠G,∴FA=FG,∴AB=CG=AF+CF
解:(1)证明:如图①,延长AE交DC的延长线于点F,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠F,
在△AEB和△FEC中,,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAF的平分线,
∴∠BAF=∠DAF,
∵AB∥CD,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
∴DF=AD=DC+CF=AB+DC
23.(1);
(2)解:成立, ,理由如下:
,
,
,
,
,
,
(3)解:存在,理由如下:
,
,
,
,
;
当时,
综上所述.
1 / 1
一、单选题
1.下列说法正确的是( )
A.两个直角三角形一定全等 B.形状相同的两个三角形全等
C.全等三角形的面积一定相等 D.面积相等的两个三角形全等
2.如图,在四边形ABCD中,AB=AD,CB=CD,点E在AC上,则图中全等三角形共有
A.1对 B.2对 C.3对 D.4对
3.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠AOB=∠A′O′B′,需要证明△COD和△C'O'D',则这两个三角形全等的依据是( )
A.SAS B.AAS C.SSS D.ASA
4.如图,中,,平分交于,过点作交于,下列结论中错误的是( )
A. B. C. D.
5.以下判断两个直角三角形全等的各种条件:(1)一个锐角和一边对应相等;(2)两对对应直角边相等;(3)两对锐角对应相等,其中能得到两个直角三角形全等的条件有( )
A.0个 B.1个 C.2个 D.3个
6.如图,AD是 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则EF=( ).
A.2.5 B.2 C.1.5 D.1
7.如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=18,DE=3,AB=7,则AC长是( )
A.5 B.6 C.4 D.7
8.如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
9.三角形是一种常见且神奇的图形,我们小学阶段就知道,三角形的内角和等于180°.如图,△ABC的角平分线BE、CD相交于点F,∠A=90°,GD//BC,BG⊥GD于点G,下列结论:①∠CBG=90°;②∠BDG=2∠ABE;③∠BFD=∠FBC+∠FCB;④∠AEB=∠EBG;⑤∠CFE=45°,其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
10.如图,在中,.分别为上的动点,且,连接,则的最小值为( )
A. B. C.6 D.
二、填空题
11. ≌ , , ,若 的周长为偶数,则 .
12.如图,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线是的平分线,由做法得到三角形全等的判定方法是 .
13.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为 .
14.如图,在中,,D,E分别是,上的点.若,则 .
15.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
16.如图,在中,,,过点B作,且,延长至点E,使,连接并延长交边于点F,若,则 .
三、解答题
17.如图,在中,,,试说明的理由.
解:已知,
▲
已知,
等式性质,
在与中,
,
≌ ,
,
又,
18.如图,,,点A、D、B、F在同一条直线上,,试说明:.
19.如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
20.如图,是的高,是的角平分线,F是中点,,.
(1)求的度数;
(2)若与的周长差为3,,则_____.
21.在中,平分交于点,点是射线上的动点(不与点重合),过点作交直线于点,的角平分线所在的直线与直线交于点(不与点重合.
(1)如图,点在线段上运动,若,,求的度数;
(2)若点在线段的延长线上时,设,求的度数(答案可用含的代数式表示).
22.阅读理解:如图①,在四边形ABCD中,ABDC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
(1)AB,AD,DC之间的等量关系为
(2)问题探究:如图②,在四边形ABCD中,ABDC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
23.已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,∠BDA=∠AEC=∠BAC
图① 图② 图③
(1)如图①,若AB⊥AC,则BD与AE的数量关系为 ,BD,CE与DE的数量关系为 ;
(2)如图②,当AB不垂直于AC时,(1)中的结论是否成立?请说明理由.
(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,DE=10cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t与x的值;若不存在,请说明理由.
答案解析部分
1.C
2.C
3.C
4.D
5.B
6.C
解:如图,延长AD,使DG=AD,连接BG,
∵AD是△ABC的中线,
∴BD=CD,且DG=AD,∠ADC=∠BDG,
∴△ADC≌△GDB(SAS),
∴AC=DG=CF+AF=6+AF,∠DAC=∠G,
∵EF=AF,
∴∠DAC=∠AEF,
∴∠G=∠AEF=∠BEG,
∴BE=BG=7.5,
∴6+AF=BG=7.5,
∴AF=1.5=EF,
故选择:C.
7.A
8.A
9.A
10.B
11.4
12.SSS
13.4
14.
15.15
16.12
解:如图,过点D作DG⊥BE交BE的延长线于点G,
∵BD⊥AB,
∴∠ABC+∠DBG=90°,
∵∠BDG+∠DBG=90°,
∴∠ABC=∠BDG,
在△ABC和△BDG中,
,
∴△ABC≌△BDG(AAS)
∴AC=BG
在△ECF和△EGD中,
,
∴△ECF≌△EGD(AAS)
∴EG=CE=BC=3,
∴AC=BG=BC+CE+EG=6+3+3=12.
17.解:(已知),
(等边对等角),
(已知),
(等式性质),
(等角对等边),
在ABD与ACD中,
,(全等三角形的对应角相等),
又,
(等腰三角形的三线合一).
18.证明:,
,
,
,
即,
在和中
,
.
19.(1)∠A=28°;(2)AB =2 cm.
20.(1);
(2).
21.(1)
(2)
22.(1)AD=AB+DC
证明:如图①,延长AE交DC的延长线于点F,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠F,
在△AEB和△FEC中,,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAF的平分线,
∴∠BAF=∠DAF,
∵AB∥CD,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
∴DF=AD=DC+CF=AB+DC;
(2)解:AB=AF+CF,证明:如下图,延长AE交DF的延长线于点G,∵E是BC的中点,∴CE=BE,∵AB∥DC,∴∠BAE=∠G,在△AEB和△GEC中,,∴△AEB≌△GEC,∴AB=GC,∵AE是∠BAF的平分线,∴∠BAG=∠FAG,∵AB∥CD,∴∠BAG=∠G,∴∠FAG=∠G,∴FA=FG,∴AB=CG=AF+CF
解:(1)证明:如图①,延长AE交DC的延长线于点F,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠F,
在△AEB和△FEC中,,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAF的平分线,
∴∠BAF=∠DAF,
∵AB∥CD,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
∴DF=AD=DC+CF=AB+DC
23.(1);
(2)解:成立, ,理由如下:
,
,
,
,
,
,
(3)解:存在,理由如下:
,
,
,
,
;
当时,
综上所述.
1 / 1
