上海市虹口区2016届九年级上学期期末考试数学试卷(解析版)
文档属性
| 名称 | 上海市虹口区2016届九年级上学期期末考试数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-04 00:00:00 | ||
图片预览




文档简介
虹口2015学年第一学期期终教学质量监控测试
初三数学 试卷
(满分150分,考试时间100分钟) 2016.1
考生注意:
1.本试卷含三个大题,共25题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题(本大题共6题,每题4分,满分24分)
[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.已知为锐角,如果,那么等于
A.; B.; C.; D.不确定.
【考点】特殊角的三角函数值 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
为锐角,,则=45°,故选B
【答案】B
2.把二次函数化成的形式是
A.; B.; C.; D..
【考点】二次函数的概念及表示方法 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
原式=,故选D
【答案】D
3.若将抛物线平移,得到新抛物线,则下列平移方法中,正确的是
A.向左平移3个单位; B.向右平移3个单位;
C.向上平移3个单位; D.向下平移3个单位.
【考点】二次函数图像的平移 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
对称轴为x=0,顶点坐标(0,0);平移后对称轴x=-3,顶点(-3,0);可知为向左平移3个单位,故选A
【答案】A
4.若坡面与水平面的夹角为,则坡度i与坡角之间的关系是
A.; B.; C.; D..
【考点】锐角三角函数 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
坡度定义为坡角的正切值,则,故选D
【答案】D
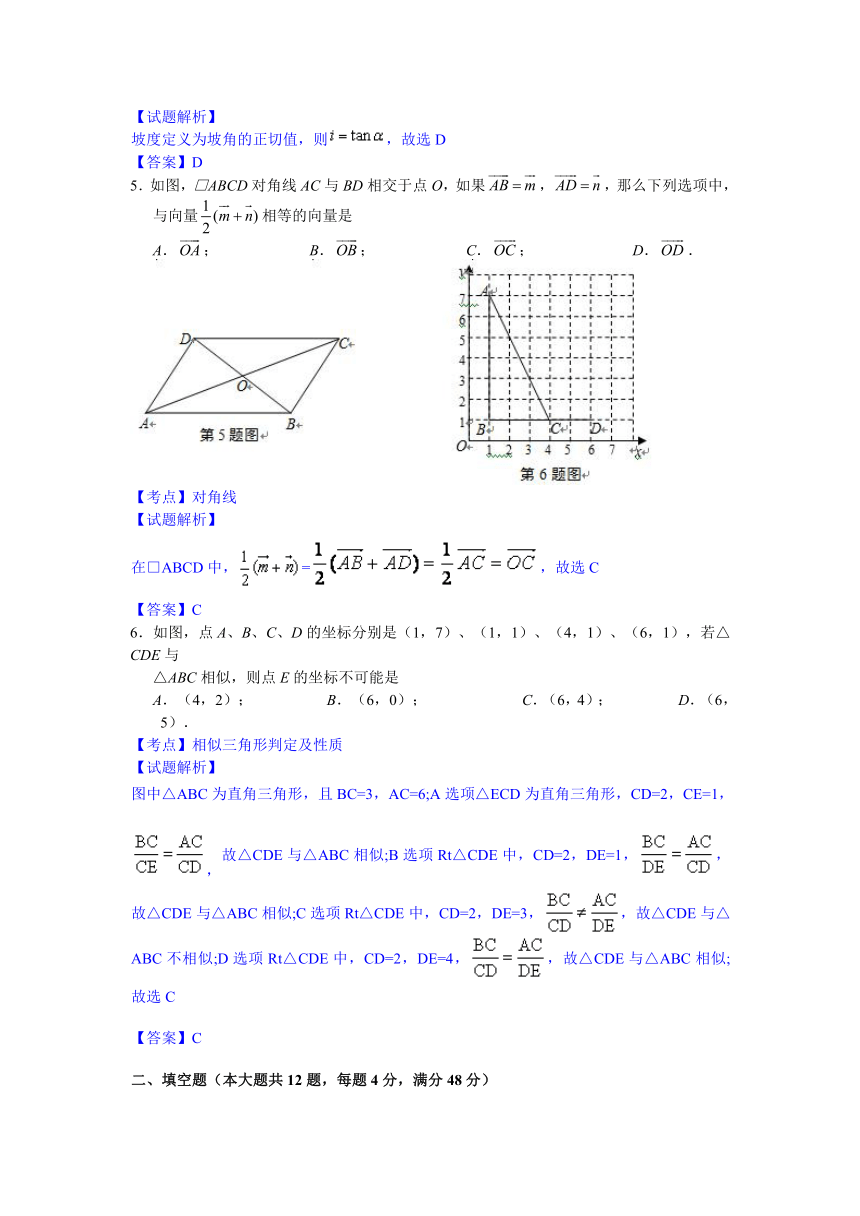
5.如图,□ABCD对角线AC与BD相交于点O,如果,,那么下列选项中,与向量相等的向量是
A.; B.; C.; D..
( http: / / www.21cnjy.com )
【考点】对角线
【试题解析】
在□ABCD中,=,故选C
【答案】C
6.如图,点A、B、C、D的坐标分别是(1,7)、(1,1)、(4,1)、(6,1),若△CDE与
△ABC相似,则点E的坐标不可能是
A.(4,2); B.(6,0); C.(6,4); D.(6,5).
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
图中△ABC为直角三角形,且BC=3,AC=6;A选项△ECD为直角三角形,CD=2,CE=1,,故△CDE与△ABC相似;B选项Rt△CDE中,CD=2,DE=1,,故△CDE与△ABC相似;C选项Rt△CDE中,CD=2,DE=3,,故△CDE与△ABC不相似;D选项Rt△CDE中,CD=2,DE=4,,故△CDE与△ABC相似;故选C
【答案】C
二、填空题(本大题共12题,每题4分,满分48分)
[请将结果直接填入答题纸的相应位置]
7.若,则的值是 ▲ .
【考点】比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
=
【答案】
8. 计算:= ▲ .
【考点】函数
【试题解析】
=
【答案】
9.二次函数的图像的对称轴是直线 ▲ .
【考点】二次函数图像与a,b,c的关系 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
的对称轴为.
【答案】
10. 如果抛物线经过原点,那么= ▲ .
【考点】二次函数表达式的确定 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
将原点(0,0)代入抛物线解析式,得-1+m=0,解得m=1.
【答案】1
11.已知点、为二次函数图像上的两点,若,则
▲ .(填“>”、“<”或“=”)
【考点】二次函数的图像及其性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
开口向上,对称轴为x=1,则当x<1时,y随x的增大而减小;因为,所以y1>y2
【答案】
12.用“描点法”画二次函数的图像时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 …
y … ﹣11 ﹣2 1 ﹣2 …
根据表格上的信息回答问题:当时,= ▲ .
【考点】二次函数的图像及其性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
观察表格中数据可以看出,当x=-1与x=1时y值相等,可得该二次函数的对称轴为,所以x=2时y值与x=-2时y值相等,查表为-11
【答案】-11
13.如果两个相似三角形的周长的比为,那么周长较小的三角形与周长较大的三角形对应
角平分线的比为 ▲ .
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
令两相似三角形分别为△ABC与△A’B’C’,其中△ABC周长较小,相似比为k,则由题意可得:,即两三角形的相似比为1:4;又相似三角形对应的角平分线比等于相似比,故角平分线之比为1:4
【答案】1:4
14. 如图,在□ABCD中,E是边BC上的点,分别联结AE、BD相交于点O,若AD=5,,则= ▲ .
( http: / / www.21cnjy.com )
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
如图,过C点作CF//AE交AD与点F,则可知在□ABCD中BO=DG,又已知,则;又AE//CF,故;又BC=AD=5,所以
【答案】2
15.如图,正方形DEFG的边EF在△A ( http: / / www.21cnjy.com )BC的边BC上,顶点D、G分别在边AB、AC上.若△ABC的边BC长为40厘米,高AH为30厘米,则正方形DEFG的边长为 ▲ 厘米.
【考点】三角形的面积 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )梯形的有关概念和性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
令正方形边长为a,则由图可知:S△ABC=S梯形DGCB+S△ADG,代入数值得方程为,解得a=,即正方形DEFG的边长为厘米.
【答案】
16.如图,在△ABC中,∠ACB=90°,若点G是△ABC的重心,,BC=4,则CG= ▲ .
( http: / / www.21cnjy.com )
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )三角形的内心、外心和重心 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
如图,延长CG交AB于D,连接AG延长交BF于E,过D点作DF//AE;在Rt△ABC中,D为斜边中点,则AD=CD=DB,.所以∠BCG=∠B,即cos∠B=,AB=BC×=6,故CD=3;又在△ABE中,DF//AE,D为AB中点,则可得F为BE中点,即EF=BE=CE;又在△CDF中,GE//DF,EF=CE,所以DG=CG=CD=1,CG=2
【答案】2
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,,则CD= ▲ .
【考点】直角三角形与勾股定理 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )解直角三角形 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
如图,延长AD、BC交于点E;AB=3,,得BE=4,又BC=2,所以EC=2;由题意可得tan∠ECD=tan∠A=,令CD=a,则DE=a;在△CDE中,根据勾股定理得,解得a=,所以CD=
【答案】
18.如图,在矩形ABCD中,AB=6,AD=10,点E是边BC的中点,联结AE,若将△ABE沿
AE翻折,点B落在点F处,联结FC,则= ▲ .
【考点】解直角三角形 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )图形的翻折 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
由题知△ABE≌△AFE,∠AEB=∠AEF,所以∠AEB+∠AEF+∠FEC=2∠AEB+∠FEC=180°;又E为BC中点,EC=BE=EF,得∠ECF=∠EFC,所以在△EFC中,∠ECF+∠EFC+∠FEC=2∠ECF+∠FEC=180°;所以∠ECF=∠BEA,cos∠ECF=cos∠BEA=
【答案】
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
计算:
【考点】特殊角的三角函数值 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
原式= =1
【答案】1
20.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)
已知一个二次函数的图像经过A(0,-3)、B(2,-3)、C(-1,0)三点.
(1)求这个二次函数的解析式;
(2)将这个二次函数图像平移,使顶点移到点P(0,-3)的位置,求所得新抛物线的表达式.
【考点】二次函数图像的平移 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )二次函数表达式的确定 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
解:(1)设所求二次函数的解析式为:,由题意得:
解得:
∴这个二次函数的解析式为
(2)∵新抛物线是由二次函数的图像平移所得
∴a=1
又∵顶点坐标是(0,-3)
∴
【答案】(1)(2)
21.(本题满分10分)
如图,//////,AB=12,CD=6,DE∶EG∶GA=3∶4∶5.
求EF和GH的长.
【考点】比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
过点D作CB的平行线,分别交EF、GH、AB于点I、J、K
∵DC∥AB ∴KB=DC=6
∴AK=6
∵EF∥AB
∴
∵DE∶EG∶GA=3∶4∶5
∴
∴
∴
同理:
∴
∴
【答案】EF;GH
22.(本题满分10分)
如图,已知楼AB高36米,从楼顶A处测得旗 ( http: / / www.21cnjy.com )杆顶C的俯角为60°,又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°,求该旗杆CD的高.(结果保留根号)
【考点】解直角三角形的实际应用 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
过点C作CG⊥AE,垂足为点G
由题意得∠CEF=45°=∠CEG,∠ACG=60°
设CG=x,
在Rt△ACG中,
在Rt△ECG中,
∵AG+EG=AE
∴
解得:
又可求得:CF=EG=
∴答:该旗杆CD的高为()米.
【答案】
( http: / / www.21cnjy.com )
23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)
如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC.
(1)求证:;
(2)求证:∠AED +∠ADC=180°.
【考点】二次函数与一次函数综合 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )二次函数与几何综合 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )二次函数表达式的确定 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
(1)∵当时,,∴C(0,3)
在Rt△COB中,∵ ∴ ∴
∴点B(6,0)
把A(2,0)、B(6,0)分别代入,得:
得
解得:
∴该抛物线表达式为
(2)∵
∴顶点D(4,-1)
∴
(3)点E的坐标是(10,8)或(16,35)
【答案】(1)(2)8(3)(10,8)或(16,35)
( http: / / www.21cnjy.com )
24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)
在平面直角坐标系xOy中,抛物线与轴分别交于点A(2,0)、点B(点B在点A的右侧),与轴交于点C,.
(1)求该抛物线的表达式;
(2)设该抛物线的顶点为D,求四边形ACBD的面积;
(3)设抛物线上的点E在第一象限,△BCE是以BC为一条直角边的直角三角形,请直接写出点E的坐标.
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
(1)在□ABCD中,AD=BC, AD∥BC
∴
∵ x=1,即 ∴
∴ AD=AB,AG=BE
∵ E为BC的中点 ∴
∴ 即
(2)∵
∴ 不妨设AB=1,则AD=x,
∵ AD∥BC ∴
∴ ,
∵ GH∥AE ∴ ∠ DGH=∠DAE
∵ AD∥BC ∴ ∠ DAE=∠AEB
∴ ∠DGH=∠AEB
在□ABCD中,∠D=∠ABE
∴△GDH ∽△EBA
∴
∴ ∴
(3)① 当点H在边DC上时,
∵ DH=3HC ∴ ∴
∵△GDH ∽ △EBA ∴
∴ 解得
②当H在DC的延长线上时,
∵ DH=3HC ∴ ∴
∵△GDH ∽ △EBA ∴
∴ 解得
综上所述,可知的值为或
【答案】(1)(2)(3)或
( http: / / www.21cnjy.com )
25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)
如图,在□ABCD中,E为边BC的中点,F为线段AE上一点,联结BF并延长交边AD于点G,过点G作AE的平行线,交射线DC于点H.设.
(1)当时,求的值;
(2)设,求关于x的函数关系式,并写出x的取值范围;
(3)当时,求x的值.
( http: / / www.21cnjy.com )
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
(1)∵∠BAE=∠DAC ∴∠BAE+∠EAC =∠DAC+∠EAC
即∠BAC=∠EAD
∵∠ABC=∠ABE +∠CBD ∠AED=∠ABE +∠BAE
∵∠CBD=∠BAE
∴∠ABC=∠AED
∴△ABC∽△AED
∴ ∴
(2)∵△ABC∽△AED
∴ 即
∵∠BAE=∠DAC
∴△ABE∽△ACD
∴∠AEB=∠ADC
∵∠AED +∠AEB =180°
∴∠AED+∠ADC=180°
【答案】见解析
G
C
A
E
D
B
第21题图
F
H
初三数学 试卷
(满分150分,考试时间100分钟) 2016.1
考生注意:
1.本试卷含三个大题,共25题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题(本大题共6题,每题4分,满分24分)
[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.已知为锐角,如果,那么等于
A.; B.; C.; D.不确定.
【考点】特殊角的三角函数值 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
为锐角,,则=45°,故选B
【答案】B
2.把二次函数化成的形式是
A.; B.; C.; D..
【考点】二次函数的概念及表示方法 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
原式=,故选D
【答案】D
3.若将抛物线平移,得到新抛物线,则下列平移方法中,正确的是
A.向左平移3个单位; B.向右平移3个单位;
C.向上平移3个单位; D.向下平移3个单位.
【考点】二次函数图像的平移 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
对称轴为x=0,顶点坐标(0,0);平移后对称轴x=-3,顶点(-3,0);可知为向左平移3个单位,故选A
【答案】A
4.若坡面与水平面的夹角为,则坡度i与坡角之间的关系是
A.; B.; C.; D..
【考点】锐角三角函数 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
坡度定义为坡角的正切值,则,故选D
【答案】D
5.如图,□ABCD对角线AC与BD相交于点O,如果,,那么下列选项中,与向量相等的向量是
A.; B.; C.; D..
( http: / / www.21cnjy.com )
【考点】对角线
【试题解析】
在□ABCD中,=,故选C
【答案】C
6.如图,点A、B、C、D的坐标分别是(1,7)、(1,1)、(4,1)、(6,1),若△CDE与
△ABC相似,则点E的坐标不可能是
A.(4,2); B.(6,0); C.(6,4); D.(6,5).
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
图中△ABC为直角三角形,且BC=3,AC=6;A选项△ECD为直角三角形,CD=2,CE=1,,故△CDE与△ABC相似;B选项Rt△CDE中,CD=2,DE=1,,故△CDE与△ABC相似;C选项Rt△CDE中,CD=2,DE=3,,故△CDE与△ABC不相似;D选项Rt△CDE中,CD=2,DE=4,,故△CDE与△ABC相似;故选C
【答案】C
二、填空题(本大题共12题,每题4分,满分48分)
[请将结果直接填入答题纸的相应位置]
7.若,则的值是 ▲ .
【考点】比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
=
【答案】
8. 计算:= ▲ .
【考点】函数
【试题解析】
=
【答案】
9.二次函数的图像的对称轴是直线 ▲ .
【考点】二次函数图像与a,b,c的关系 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
的对称轴为.
【答案】
10. 如果抛物线经过原点,那么= ▲ .
【考点】二次函数表达式的确定 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
将原点(0,0)代入抛物线解析式,得-1+m=0,解得m=1.
【答案】1
11.已知点、为二次函数图像上的两点,若,则
▲ .(填“>”、“<”或“=”)
【考点】二次函数的图像及其性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
开口向上,对称轴为x=1,则当x<1时,y随x的增大而减小;因为,所以y1>y2
【答案】
12.用“描点法”画二次函数的图像时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 …
y … ﹣11 ﹣2 1 ﹣2 …
根据表格上的信息回答问题:当时,= ▲ .
【考点】二次函数的图像及其性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
观察表格中数据可以看出,当x=-1与x=1时y值相等,可得该二次函数的对称轴为,所以x=2时y值与x=-2时y值相等,查表为-11
【答案】-11
13.如果两个相似三角形的周长的比为,那么周长较小的三角形与周长较大的三角形对应
角平分线的比为 ▲ .
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
令两相似三角形分别为△ABC与△A’B’C’,其中△ABC周长较小,相似比为k,则由题意可得:,即两三角形的相似比为1:4;又相似三角形对应的角平分线比等于相似比,故角平分线之比为1:4
【答案】1:4
14. 如图,在□ABCD中,E是边BC上的点,分别联结AE、BD相交于点O,若AD=5,,则= ▲ .
( http: / / www.21cnjy.com )
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
如图,过C点作CF//AE交AD与点F,则可知在□ABCD中BO=DG,又已知,则;又AE//CF,故;又BC=AD=5,所以
【答案】2
15.如图,正方形DEFG的边EF在△A ( http: / / www.21cnjy.com )BC的边BC上,顶点D、G分别在边AB、AC上.若△ABC的边BC长为40厘米,高AH为30厘米,则正方形DEFG的边长为 ▲ 厘米.
【考点】三角形的面积 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )梯形的有关概念和性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
令正方形边长为a,则由图可知:S△ABC=S梯形DGCB+S△ADG,代入数值得方程为,解得a=,即正方形DEFG的边长为厘米.
【答案】
16.如图,在△ABC中,∠ACB=90°,若点G是△ABC的重心,,BC=4,则CG= ▲ .
( http: / / www.21cnjy.com )
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )三角形的内心、外心和重心 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
如图,延长CG交AB于D,连接AG延长交BF于E,过D点作DF//AE;在Rt△ABC中,D为斜边中点,则AD=CD=DB,.所以∠BCG=∠B,即cos∠B=,AB=BC×=6,故CD=3;又在△ABE中,DF//AE,D为AB中点,则可得F为BE中点,即EF=BE=CE;又在△CDF中,GE//DF,EF=CE,所以DG=CG=CD=1,CG=2
【答案】2
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,,则CD= ▲ .
【考点】直角三角形与勾股定理 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )解直角三角形 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
如图,延长AD、BC交于点E;AB=3,,得BE=4,又BC=2,所以EC=2;由题意可得tan∠ECD=tan∠A=,令CD=a,则DE=a;在△CDE中,根据勾股定理得,解得a=,所以CD=
【答案】
18.如图,在矩形ABCD中,AB=6,AD=10,点E是边BC的中点,联结AE,若将△ABE沿
AE翻折,点B落在点F处,联结FC,则= ▲ .
【考点】解直角三角形 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )图形的翻折 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
由题知△ABE≌△AFE,∠AEB=∠AEF,所以∠AEB+∠AEF+∠FEC=2∠AEB+∠FEC=180°;又E为BC中点,EC=BE=EF,得∠ECF=∠EFC,所以在△EFC中,∠ECF+∠EFC+∠FEC=2∠ECF+∠FEC=180°;所以∠ECF=∠BEA,cos∠ECF=cos∠BEA=
【答案】
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
计算:
【考点】特殊角的三角函数值 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
原式= =1
【答案】1
20.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)
已知一个二次函数的图像经过A(0,-3)、B(2,-3)、C(-1,0)三点.
(1)求这个二次函数的解析式;
(2)将这个二次函数图像平移,使顶点移到点P(0,-3)的位置,求所得新抛物线的表达式.
【考点】二次函数图像的平移 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )二次函数表达式的确定 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
解:(1)设所求二次函数的解析式为:,由题意得:
解得:
∴这个二次函数的解析式为
(2)∵新抛物线是由二次函数的图像平移所得
∴a=1
又∵顶点坐标是(0,-3)
∴
【答案】(1)(2)
21.(本题满分10分)
如图,//////,AB=12,CD=6,DE∶EG∶GA=3∶4∶5.
求EF和GH的长.
【考点】比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
过点D作CB的平行线,分别交EF、GH、AB于点I、J、K
∵DC∥AB ∴KB=DC=6
∴AK=6
∵EF∥AB
∴
∵DE∶EG∶GA=3∶4∶5
∴
∴
∴
同理:
∴
∴
【答案】EF;GH
22.(本题满分10分)
如图,已知楼AB高36米,从楼顶A处测得旗 ( http: / / www.21cnjy.com )杆顶C的俯角为60°,又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°,求该旗杆CD的高.(结果保留根号)
【考点】解直角三角形的实际应用 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
过点C作CG⊥AE,垂足为点G
由题意得∠CEF=45°=∠CEG,∠ACG=60°
设CG=x,
在Rt△ACG中,
在Rt△ECG中,
∵AG+EG=AE
∴
解得:
又可求得:CF=EG=
∴答:该旗杆CD的高为()米.
【答案】
( http: / / www.21cnjy.com )
23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)
如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC.
(1)求证:;
(2)求证:∠AED +∠ADC=180°.
【考点】二次函数与一次函数综合 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )二次函数与几何综合 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )二次函数表达式的确定 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
(1)∵当时,,∴C(0,3)
在Rt△COB中,∵ ∴ ∴
∴点B(6,0)
把A(2,0)、B(6,0)分别代入,得:
得
解得:
∴该抛物线表达式为
(2)∵
∴顶点D(4,-1)
∴
(3)点E的坐标是(10,8)或(16,35)
【答案】(1)(2)8(3)(10,8)或(16,35)
( http: / / www.21cnjy.com )
24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)
在平面直角坐标系xOy中,抛物线与轴分别交于点A(2,0)、点B(点B在点A的右侧),与轴交于点C,.
(1)求该抛物线的表达式;
(2)设该抛物线的顶点为D,求四边形ACBD的面积;
(3)设抛物线上的点E在第一象限,△BCE是以BC为一条直角边的直角三角形,请直接写出点E的坐标.
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )比例线段的相关概念及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
(1)在□ABCD中,AD=BC, AD∥BC
∴
∵ x=1,即 ∴
∴ AD=AB,AG=BE
∵ E为BC的中点 ∴
∴ 即
(2)∵
∴ 不妨设AB=1,则AD=x,
∵ AD∥BC ∴
∴ ,
∵ GH∥AE ∴ ∠ DGH=∠DAE
∵ AD∥BC ∴ ∠ DAE=∠AEB
∴ ∠DGH=∠AEB
在□ABCD中,∠D=∠ABE
∴△GDH ∽△EBA
∴
∴ ∴
(3)① 当点H在边DC上时,
∵ DH=3HC ∴ ∴
∵△GDH ∽ △EBA ∴
∴ 解得
②当H在DC的延长线上时,
∵ DH=3HC ∴ ∴
∵△GDH ∽ △EBA ∴
∴ 解得
综上所述,可知的值为或
【答案】(1)(2)(3)或
( http: / / www.21cnjy.com )
25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)
如图,在□ABCD中,E为边BC的中点,F为线段AE上一点,联结BF并延长交边AD于点G,过点G作AE的平行线,交射线DC于点H.设.
(1)当时,求的值;
(2)设,求关于x的函数关系式,并写出x的取值范围;
(3)当时,求x的值.
( http: / / www.21cnjy.com )
【考点】相似三角形判定及性质 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "http: / / www. / shiti / _blank )
【试题解析】
(1)∵∠BAE=∠DAC ∴∠BAE+∠EAC =∠DAC+∠EAC
即∠BAC=∠EAD
∵∠ABC=∠ABE +∠CBD ∠AED=∠ABE +∠BAE
∵∠CBD=∠BAE
∴∠ABC=∠AED
∴△ABC∽△AED
∴ ∴
(2)∵△ABC∽△AED
∴ 即
∵∠BAE=∠DAC
∴△ABE∽△ACD
∴∠AEB=∠ADC
∵∠AED +∠AEB =180°
∴∠AED+∠ADC=180°
【答案】见解析
G
C
A
E
D
B
第21题图
F
H
同课章节目录
