第八单元数学广角——数与形巩固练 人教版数学六年级上册(含答案)
文档属性
| 名称 | 第八单元数学广角——数与形巩固练 人教版数学六年级上册(含答案) | 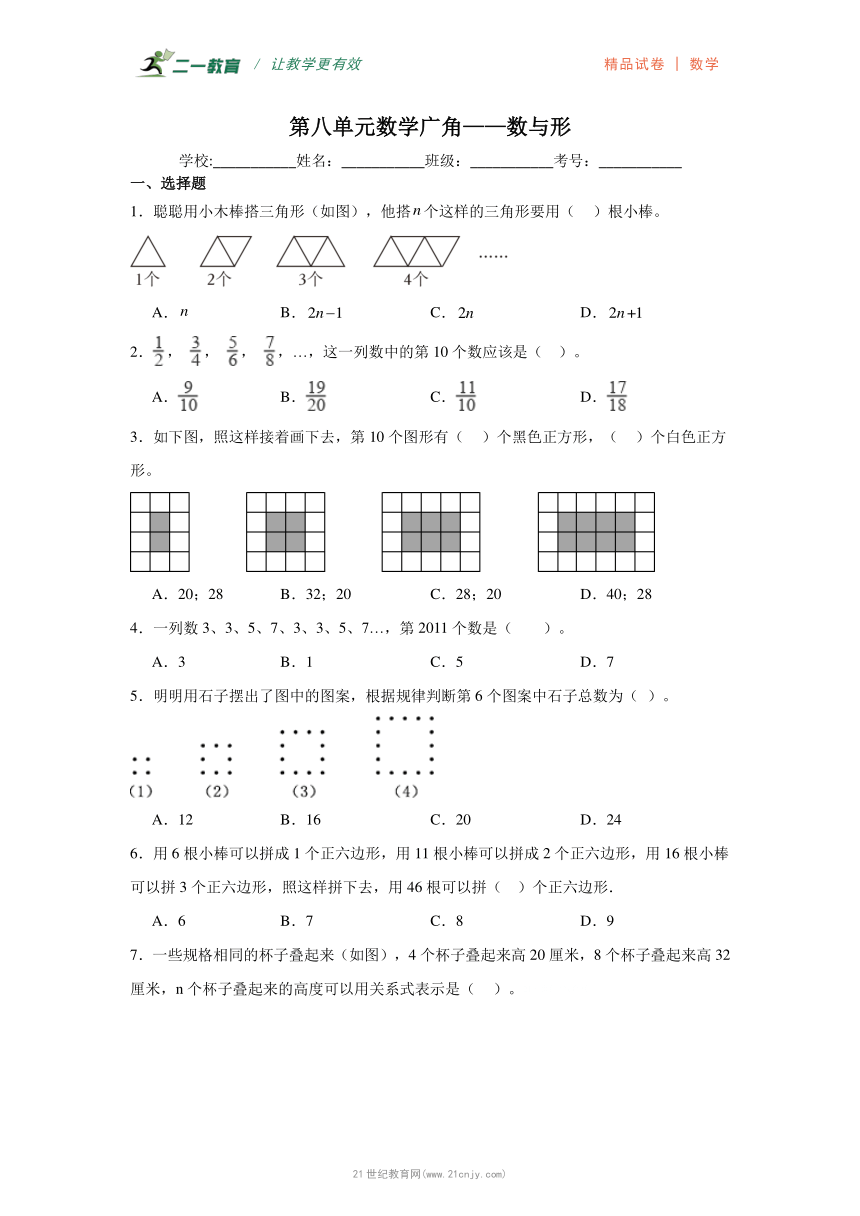 | |
| 格式 | doc | ||
| 文件大小 | 687.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 12:05:16 | ||
图片预览





文档简介
/ 让教学更有效 精品试卷 | 数学
第八单元数学广角——数与形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.聪聪用小木棒搭三角形(如图),他搭个这样的三角形要用( )根小棒。
A. B. C. D.
2., , , ,…,这一列数中的第10个数应该是( )。
A. B. C. D.
3.如下图,照这样接着画下去,第10个图形有( )个黑色正方形,( )个白色正方形。
A.20;28 B.32;20 C.28;20 D.40;28
4.一列数3、3、5、7、3、3、5、7…,第2011个数是( )。
A.3 B.1 C.5 D.7
5.明明用石子摆出了图中的图案,根据规律判断第6个图案中石子总数为( )。
A.12 B.16 C.20 D.24
6.用6根小棒可以拼成1个正六边形,用11根小棒可以拼成2个正六边形,用16根小棒可以拼3个正六边形,照这样拼下去,用46根可以拼( )个正六边形.
A.6 B.7 C.8 D.9
7.一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,8个杯子叠起来高32厘米,n个杯子叠起来的高度可以用关系式表示是( )。21·世纪*教育网
A.5n B.4n C.4n+12 D.3n+8
8.摆1个正方形需要4根小棒,摆2个正方形需要7根小棒.照这样横着摆下去,10个正方形需要( )根小棒。【版权所有:21教育】
A.31 B.30 C.27 D.32
二、填空题
9.下图中有( )个三角形.
10.观察下面的点阵图规律,第9个点阵图中有( )个点。
11.用长度相等的火柴棒按照下图的方式拼摆正方形,第1幅图需要4根火柴棒,第2幅图需要7根火柴棒,第3幅图需要10根火柴棒。按照这个规律,第4幅图需要( )根火柴棒,第7幅图需要( )根火柴棒。21教育名师原创作品
12.如图,摆一个三角形需要3根小棒;摆2个三角形需要5根小棒,摆3个三角形需要7根小棒。照这样摆下去,摆6个三角形需要( )根小棒,摆10个三角形需要( )根小棒,摆n个三角形需要( )根小棒。
13.观察下图,填空.
( )个三角形 ( )个三角形 ( )个三角形
14.观察下面的点阵图规律,第9个点阵图中有( )个点,第( )个点阵图中有300个点。
15.观察规律,直接写一写:1=12,1+3=22,1+3+5=32,1+3+5+7=42…,( )=112。
16.已知:1×7+1=8,12×7+2=86,123×7+3=864,1234×7+4=8642;那么:12345×7+5=( )。
三、判断题
17.在扇形统计图中,所有扇形的百分比之和为1。( )
18.扇形统计图中,各部分数量占总数的百分比的总和都是100%。( )
19.如图这样放三角形积木,如果最下层放19块积木,共需放72块积木。( )
20.要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制扇形统计图。( )
21.下图是小明和小敏两人在相同的600米路上步行情况统计图,从图中可以看出小敏的速度更快。( )
四、解答题
22.平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?
23.观察如图,要想得到200个直角三角形,应画多少个正方形?
……
24.在10×19方格表的每个方格内,写上0或1,然后算出每行及每列的各数之和。问最多能得到多少个不同的和数?www.21-cn-jy.com
25.按照右边的方法堆木头,如果底层放9根木头,完成堆放后,木头的总根数是多少根?
参考答案:
1.D
【分析】根据图意,1个三角形用根火柴,2个三角形用根火柴,3个三角形用根火柴,则个三角形用根火柴,据此解答即可。
【详解】分析可知,用小木棒搭三角形(如图),他搭个这样的三角形要用根小棒。
故答案为:D
2.B
【详解】从这列数中可以看出每一个数的分母就是这个数在这列数中的顺序×2,每一个数的分子就是分母-1。www-2-1-cnjy-com
故答案为:B
3.A
【分析】分析题意,找出图形变化的规律,用含有字母的式子表示出第n个图形小正方形的总个数和黑色小正方形的个数;
白色小正方形的个数=小正方形的总个数-黑色小正方形的个数,据此解答。
【详解】第n个图形小正方形的总个数:4×(n+2)=4n+8
第n个图形黑色小正方形的个数:2n
第n个图形白色小正方形的个数:4n+8-2n=2n+8
当n=10时
黑色小正方形的个数:2n=2×10=20(个)
白色小正方形的个数:2n+8=2×10+8=28(个)
故答案为:A
【点睛】用含有字母的式子表示出图形变化的规律是解答题目的关键。
4.C
【解析】3、3、5、7,4个数是一个循环,要求第2011个数是几,用2011除以4,余数是几,就在3、3、5、7中选第几个数,因此得解.据此进行判断即可解答。
【详解】2011÷4=502……3
所以第2011个数是5。
故选:C
【点睛】此题考查了数列中的规律,看出规律,灵活应用有余数的除法运算而得解。
5.D
【分析】图(1)石子总数是4,图(2)石子总数是8,图(3)石子总数是12,图(4)石子总数是16,从中找出规律:石子的总数=图案序号×4,从而可以求出第6个图案中石子总数。21教育网
【详解】据分析知:6×4=24(个)
故答案为:D
【点睛】通过已知图案,找出规律:石子的总数=图案序号×4,这是解决此题的关键。
6.D
【详解】略
7.D
【分析】先计算增加一个杯子时增加的高度,再计算出单独一个杯子的高度,n个杯子叠起来的高度表示为:单独一个杯子的高度+(n-1)×增加一个杯子时增加的高度。
【详解】增加一个杯子时增加的高度:(32-20)÷4=12÷4=3(厘米)
单独一个杯子的高度:20-3×(4-1)=20-3×3=20-9=11(厘米)
11+(n-1)×3
=11+3n-3
=3n+8
故答案为:D
【点睛】掌握含有字母的式子的化简方法是解答本题的关键。
8.A
【详解】摆1个正方形需要小棒根数:4根
摆2个正方形需要小棒根数:4+3=7(根)
摆3个正方形需要小棒根数:4+3+3=10(根)
……
摆n个正方形需要小棒根数:4+3(n﹣1)=(3n+1)根
……
摆10个正方形需要小棒根数:
3×10+1
=30+1
=31(根)
故答案为:A
9.15
【详解】略
10.30
【分析】观察点阵图可以发现:以左下角的3个点为基础,每个点阵图依次增加3个点,那么第1个点阵图中有3×(1+1)=6个点;第2个点阵图有3×(2+1)=9个点;第3个点阵图中有3×(3+1)=12个点;以此类推,第n个点阵图中有3(n+1)个点。据此解答。21世纪教育网版权所有
【详解】通过分析,第n个点阵图中有3(n+1)个点。
3×(9+1)
=3×10
=30(个)
则第9个点阵图中有30个点。
【点睛】本题考查数形结合问题。通过观察、分析,发现点阵图的序数与点的个数之间的关系是解题的关键。
11. 13 22
【分析】观察这组图,可知每增加1个正方形,需要3根火柴棒。摆1个正方形需要4根火柴棒,摆2个正方形需要(4+3)根火柴棒,摆3个正方形需要(4+2×3)根火柴棒,则摆4个正方形需要(4+3×3)根火柴棒,摆7个正方形需要(4+6×3)根火柴棒。
【详解】4+(4-1)×3
=4+3×3
=4+9
=13(根)
4+(7-1)×3
=4+6×3
=4+18
=22(根)
第4幅图需要13根火柴棒,第7幅图需要22根火柴棒。
【点睛】本题考查数与形,关键是明确正方形个数与火柴棒根数之间的关系。
12. 13 21 (2n+1)
【分析】结合图形可知,第一个图形需要需要3根小棒,后面每多一个图形,则多用2根小棒,搭建n个图形,则需要3+2(n-1)=2n+1(根),由此解答即可。
【详解】第一个图形需要需要3根小棒,后面每多一个图形,则多用2根小棒,搭建n个图形,则需要3+2(n-1)=2n+1(根),21·cn·jy·com
当摆6个三角形时需:2n+1=2×6+1=13(根)
当摆10个三角形时需:2n+1=2×10+1=21(根)
【点睛】此题考查数与形,根据已知信息得出小棒的变化规律是解题的关键。
13. 3 6 10
【解析】略
14. 30 99
【分析】通过观察,第1幅点阵图中有(3+3)个点,第2幅点阵图中有(3+3+3)个点;第3幅点阵图中有(3+3+3+3)个点……以此类推,可得出第n幅点阵图中有(3+3n)个点,据此解答。
【详解】据分析可知,第n幅点阵图中有(3+3n)个点;
第9幅点阵图中有
3+3×9
=3+27
=30(个)
第9幅点阵图中有30个点。
3+3n=300
解:3+3n-3=300-3
3n=297
3n÷3=297÷3
n=99
第99个点阵图中有300个点。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
15.1+3+5+7+9+11+13+15+17+19+21
【分析】观察算式,每相邻两个加数相差2,加数都是连续的奇数,发现规律:连续奇数的和等于奇数个数的平方,据此规律解答。21*cnjy*com
【详解】1+3+5+7+9+11+13+15+17+19+21=112
【点睛】本题是找规律的题型,从已知的数据中找到规律,并按规律解题。
16.86420
【分析】观察算式可知,乘法算式第一个因数依次为1、12、123、1234、12345,因数的位数每次递增一位且它们是连续自然数,乘法算式的第二个因数都是7,加号后面的数字依次为1、2、3、4、5,它们是从1开始的连续自然数,算式的结果依次为8、86、864、8642,算式结果的位数每次递增一位,且它们是从8开始依次递减的连续偶数,所以12345×7+5的结果是一个五位数,前四位数字是8642,最后一位数字是0,据此解答。
【详解】分析可知,已知:1×7+1=8,12×7+2=86,123×7+3=864,1234×7+4=8642;那么:12345×7+5=86420。21cnjy.com
【点睛】根据已知条件找出算式变化的规律是解答题目的关键。
17.√
【分析】扇形统计图中,将整个圆看作单位“1”,则所有扇形的百分比之和为1。
【详解】在扇形统计图中,所有扇形的百分比之和为1,题目描述正确。
故答案为:√
【点睛】本题主要考查扇形统计图的概念和意义,圆代表整体,即单位“1”,各个扇形代表部分,掌握扇形统计图的特点是关键。
18.√
【分析】在扇形统计图中,整个圆代表总体,把总体看作单位“1”,每个扇形代表总体中的各部分,各部分之和等于单位“1”,即各部分数量占总数的百分比的总和都是100%。
【详解】分析可知,任何扇形统计图中,各部分数量占总数的百分比的总和都是100%。
故答案为:√
【点睛】扇形统计图是用圆的面积表示总数,用圆内扇形的面积表示各部分占总数的百分比。
19.×
【分析】图1:1+3=4;图2:1+3+5=9;图3:1+3+5+7=16,结合规律可知:如果最下层放19块积木,共需放积木的块数为:1+3+5+……+19=(1+19)×10÷2,计算出结果判断即可。2-1-c-n-j-y
【详解】1+3+5+……+19
=(1+19)×10÷2
=20÷2×10
=10×10
=100
故答案为:×
【点睛】本题考查数和形中的找规律问题。找到共同特征解决问题即可。
20.×
【分析】扇形统计图主要表示部分与部分之间,部分与总体之间的数量关系,以及各部分量占总体的百分比情况,要具体的数量选择条形统计图更加合适,据此解答。
【详解】条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;因此要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制条形统计图。
故答案为:×
【点睛】根据统计图的特征选择合适的统计图是解答题目的关键。
21.×
【分析】如图所示,横向表示所用时间,竖向表示行走的行程,行程相同的情况下,线段越陡的速度越快。
【详解】通过观察可知,小明步行600米所用时间是5分钟,小敏步行600米所用时间是6分钟。
故答案为:×
【点睛】解答本题需要明确折线统计图自身的特点,例如横轴、纵轴所代表的含义,并能够利用现有信息进行计算,从而求解。【来源:21cnj*y.co*m】
22.16部分;5051部分
【分析】要使得分成的份数尽可能多,就要求直线的交点尽可能多,新增加的直线必须和每一条直线都相交,如图,给出比较简单的情况,0条直线,可以分成1部分,1条直线,可以分成2部分,2条直线,可以分成4部分,每一次增加的份数是连续的自然数列。
【详解】如图所示:
假设用ak表示k条直线最多能把圆的内部分成的部分数,这里k=0,1,2,…
a0=1
a1=a0+1=2
a2=a1+2=4
a3=a2+3=7
a4=a3+4=11
…
答:5条直线可以把圆分成16部分;100条直线可以把圆分成5051部分。
【点睛】本题考查的是归纳递推计数问题,n条直线最多能把圆的内部分成部分。
23.51个
【分析】第1个正方体中有0个直角三角形;第2个正方体中有4个直角三角形;第3个正方体中有8个直角三角形;第4个正方体中有12个直角三角形。由此得出规律,三角形的个数都是4的倍数,然后得出假设第n个正方体,就有(n-1)×4个直角三角形。
【详解】根据图中的数据可得:1个正方形有0个三角形,可以写成(1-1)×4个;
2个正方形有4个三角形,可以写成(2-1)×4个;
3个正方形有8个三角形,可以写成(3-1)×4个;
4个正方形有12个三角形,可以写成(4-1)×4个;
所以当正方形的个数为a时,三角形的个数可以写成:(a-1)×4个;
设需要画a个正方形才得到200个直角三角形,则根据上面的结论可得:
(a-1)×4=200
a-1=200÷4
a-1=50
a=51
答:应画51个正方形。
【点睛】本题的关键是根据图形发现规律:第1个正方体就有0×4个直角三角形;第2个正方体就有(2-1)×4个直角三角形,然后以此类推。2·1·c·n·j·y
24.19个
【分析】每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。21*cnjy*com
【详解】首先每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。如果和是0出现,那么必然有另外一个数字不能出现。如果0出现在行的和中,说明有1行全是0,意味着列的和中至多出现0到9,加上行的和至多出现10个数字,所以少了一种可能。如果0出现在列的和中,说明在行的和中19不可能出现,所以0出现就意味着另一个数字不能出现,所以至多是19。如下图所示:【出处:21教育名师】
除去重复的和,所以和最多是19个。
答: 最多能得到19个不同的和数。
【点睛】我们先弄清楚题意,分行分列的分别求出和,最后算出不同和的个数,综合考虑此题中最小和是0,最大和是19。假设每一行全写0则和是0,写上1个1则和是1,以此类推可得出最多的和的个数是19个。【来源:21·世纪·教育·网】
25.45根
【详解】9×(9+1)÷2 = 45(根)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第八单元数学广角——数与形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.聪聪用小木棒搭三角形(如图),他搭个这样的三角形要用( )根小棒。
A. B. C. D.
2., , , ,…,这一列数中的第10个数应该是( )。
A. B. C. D.
3.如下图,照这样接着画下去,第10个图形有( )个黑色正方形,( )个白色正方形。
A.20;28 B.32;20 C.28;20 D.40;28
4.一列数3、3、5、7、3、3、5、7…,第2011个数是( )。
A.3 B.1 C.5 D.7
5.明明用石子摆出了图中的图案,根据规律判断第6个图案中石子总数为( )。
A.12 B.16 C.20 D.24
6.用6根小棒可以拼成1个正六边形,用11根小棒可以拼成2个正六边形,用16根小棒可以拼3个正六边形,照这样拼下去,用46根可以拼( )个正六边形.
A.6 B.7 C.8 D.9
7.一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,8个杯子叠起来高32厘米,n个杯子叠起来的高度可以用关系式表示是( )。21·世纪*教育网
A.5n B.4n C.4n+12 D.3n+8
8.摆1个正方形需要4根小棒,摆2个正方形需要7根小棒.照这样横着摆下去,10个正方形需要( )根小棒。【版权所有:21教育】
A.31 B.30 C.27 D.32
二、填空题
9.下图中有( )个三角形.
10.观察下面的点阵图规律,第9个点阵图中有( )个点。
11.用长度相等的火柴棒按照下图的方式拼摆正方形,第1幅图需要4根火柴棒,第2幅图需要7根火柴棒,第3幅图需要10根火柴棒。按照这个规律,第4幅图需要( )根火柴棒,第7幅图需要( )根火柴棒。21教育名师原创作品
12.如图,摆一个三角形需要3根小棒;摆2个三角形需要5根小棒,摆3个三角形需要7根小棒。照这样摆下去,摆6个三角形需要( )根小棒,摆10个三角形需要( )根小棒,摆n个三角形需要( )根小棒。
13.观察下图,填空.
( )个三角形 ( )个三角形 ( )个三角形
14.观察下面的点阵图规律,第9个点阵图中有( )个点,第( )个点阵图中有300个点。
15.观察规律,直接写一写:1=12,1+3=22,1+3+5=32,1+3+5+7=42…,( )=112。
16.已知:1×7+1=8,12×7+2=86,123×7+3=864,1234×7+4=8642;那么:12345×7+5=( )。
三、判断题
17.在扇形统计图中,所有扇形的百分比之和为1。( )
18.扇形统计图中,各部分数量占总数的百分比的总和都是100%。( )
19.如图这样放三角形积木,如果最下层放19块积木,共需放72块积木。( )
20.要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制扇形统计图。( )
21.下图是小明和小敏两人在相同的600米路上步行情况统计图,从图中可以看出小敏的速度更快。( )
四、解答题
22.平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?
23.观察如图,要想得到200个直角三角形,应画多少个正方形?
……
24.在10×19方格表的每个方格内,写上0或1,然后算出每行及每列的各数之和。问最多能得到多少个不同的和数?www.21-cn-jy.com
25.按照右边的方法堆木头,如果底层放9根木头,完成堆放后,木头的总根数是多少根?
参考答案:
1.D
【分析】根据图意,1个三角形用根火柴,2个三角形用根火柴,3个三角形用根火柴,则个三角形用根火柴,据此解答即可。
【详解】分析可知,用小木棒搭三角形(如图),他搭个这样的三角形要用根小棒。
故答案为:D
2.B
【详解】从这列数中可以看出每一个数的分母就是这个数在这列数中的顺序×2,每一个数的分子就是分母-1。www-2-1-cnjy-com
故答案为:B
3.A
【分析】分析题意,找出图形变化的规律,用含有字母的式子表示出第n个图形小正方形的总个数和黑色小正方形的个数;
白色小正方形的个数=小正方形的总个数-黑色小正方形的个数,据此解答。
【详解】第n个图形小正方形的总个数:4×(n+2)=4n+8
第n个图形黑色小正方形的个数:2n
第n个图形白色小正方形的个数:4n+8-2n=2n+8
当n=10时
黑色小正方形的个数:2n=2×10=20(个)
白色小正方形的个数:2n+8=2×10+8=28(个)
故答案为:A
【点睛】用含有字母的式子表示出图形变化的规律是解答题目的关键。
4.C
【解析】3、3、5、7,4个数是一个循环,要求第2011个数是几,用2011除以4,余数是几,就在3、3、5、7中选第几个数,因此得解.据此进行判断即可解答。
【详解】2011÷4=502……3
所以第2011个数是5。
故选:C
【点睛】此题考查了数列中的规律,看出规律,灵活应用有余数的除法运算而得解。
5.D
【分析】图(1)石子总数是4,图(2)石子总数是8,图(3)石子总数是12,图(4)石子总数是16,从中找出规律:石子的总数=图案序号×4,从而可以求出第6个图案中石子总数。21教育网
【详解】据分析知:6×4=24(个)
故答案为:D
【点睛】通过已知图案,找出规律:石子的总数=图案序号×4,这是解决此题的关键。
6.D
【详解】略
7.D
【分析】先计算增加一个杯子时增加的高度,再计算出单独一个杯子的高度,n个杯子叠起来的高度表示为:单独一个杯子的高度+(n-1)×增加一个杯子时增加的高度。
【详解】增加一个杯子时增加的高度:(32-20)÷4=12÷4=3(厘米)
单独一个杯子的高度:20-3×(4-1)=20-3×3=20-9=11(厘米)
11+(n-1)×3
=11+3n-3
=3n+8
故答案为:D
【点睛】掌握含有字母的式子的化简方法是解答本题的关键。
8.A
【详解】摆1个正方形需要小棒根数:4根
摆2个正方形需要小棒根数:4+3=7(根)
摆3个正方形需要小棒根数:4+3+3=10(根)
……
摆n个正方形需要小棒根数:4+3(n﹣1)=(3n+1)根
……
摆10个正方形需要小棒根数:
3×10+1
=30+1
=31(根)
故答案为:A
9.15
【详解】略
10.30
【分析】观察点阵图可以发现:以左下角的3个点为基础,每个点阵图依次增加3个点,那么第1个点阵图中有3×(1+1)=6个点;第2个点阵图有3×(2+1)=9个点;第3个点阵图中有3×(3+1)=12个点;以此类推,第n个点阵图中有3(n+1)个点。据此解答。21世纪教育网版权所有
【详解】通过分析,第n个点阵图中有3(n+1)个点。
3×(9+1)
=3×10
=30(个)
则第9个点阵图中有30个点。
【点睛】本题考查数形结合问题。通过观察、分析,发现点阵图的序数与点的个数之间的关系是解题的关键。
11. 13 22
【分析】观察这组图,可知每增加1个正方形,需要3根火柴棒。摆1个正方形需要4根火柴棒,摆2个正方形需要(4+3)根火柴棒,摆3个正方形需要(4+2×3)根火柴棒,则摆4个正方形需要(4+3×3)根火柴棒,摆7个正方形需要(4+6×3)根火柴棒。
【详解】4+(4-1)×3
=4+3×3
=4+9
=13(根)
4+(7-1)×3
=4+6×3
=4+18
=22(根)
第4幅图需要13根火柴棒,第7幅图需要22根火柴棒。
【点睛】本题考查数与形,关键是明确正方形个数与火柴棒根数之间的关系。
12. 13 21 (2n+1)
【分析】结合图形可知,第一个图形需要需要3根小棒,后面每多一个图形,则多用2根小棒,搭建n个图形,则需要3+2(n-1)=2n+1(根),由此解答即可。
【详解】第一个图形需要需要3根小棒,后面每多一个图形,则多用2根小棒,搭建n个图形,则需要3+2(n-1)=2n+1(根),21·cn·jy·com
当摆6个三角形时需:2n+1=2×6+1=13(根)
当摆10个三角形时需:2n+1=2×10+1=21(根)
【点睛】此题考查数与形,根据已知信息得出小棒的变化规律是解题的关键。
13. 3 6 10
【解析】略
14. 30 99
【分析】通过观察,第1幅点阵图中有(3+3)个点,第2幅点阵图中有(3+3+3)个点;第3幅点阵图中有(3+3+3+3)个点……以此类推,可得出第n幅点阵图中有(3+3n)个点,据此解答。
【详解】据分析可知,第n幅点阵图中有(3+3n)个点;
第9幅点阵图中有
3+3×9
=3+27
=30(个)
第9幅点阵图中有30个点。
3+3n=300
解:3+3n-3=300-3
3n=297
3n÷3=297÷3
n=99
第99个点阵图中有300个点。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
15.1+3+5+7+9+11+13+15+17+19+21
【分析】观察算式,每相邻两个加数相差2,加数都是连续的奇数,发现规律:连续奇数的和等于奇数个数的平方,据此规律解答。21*cnjy*com
【详解】1+3+5+7+9+11+13+15+17+19+21=112
【点睛】本题是找规律的题型,从已知的数据中找到规律,并按规律解题。
16.86420
【分析】观察算式可知,乘法算式第一个因数依次为1、12、123、1234、12345,因数的位数每次递增一位且它们是连续自然数,乘法算式的第二个因数都是7,加号后面的数字依次为1、2、3、4、5,它们是从1开始的连续自然数,算式的结果依次为8、86、864、8642,算式结果的位数每次递增一位,且它们是从8开始依次递减的连续偶数,所以12345×7+5的结果是一个五位数,前四位数字是8642,最后一位数字是0,据此解答。
【详解】分析可知,已知:1×7+1=8,12×7+2=86,123×7+3=864,1234×7+4=8642;那么:12345×7+5=86420。21cnjy.com
【点睛】根据已知条件找出算式变化的规律是解答题目的关键。
17.√
【分析】扇形统计图中,将整个圆看作单位“1”,则所有扇形的百分比之和为1。
【详解】在扇形统计图中,所有扇形的百分比之和为1,题目描述正确。
故答案为:√
【点睛】本题主要考查扇形统计图的概念和意义,圆代表整体,即单位“1”,各个扇形代表部分,掌握扇形统计图的特点是关键。
18.√
【分析】在扇形统计图中,整个圆代表总体,把总体看作单位“1”,每个扇形代表总体中的各部分,各部分之和等于单位“1”,即各部分数量占总数的百分比的总和都是100%。
【详解】分析可知,任何扇形统计图中,各部分数量占总数的百分比的总和都是100%。
故答案为:√
【点睛】扇形统计图是用圆的面积表示总数,用圆内扇形的面积表示各部分占总数的百分比。
19.×
【分析】图1:1+3=4;图2:1+3+5=9;图3:1+3+5+7=16,结合规律可知:如果最下层放19块积木,共需放积木的块数为:1+3+5+……+19=(1+19)×10÷2,计算出结果判断即可。2-1-c-n-j-y
【详解】1+3+5+……+19
=(1+19)×10÷2
=20÷2×10
=10×10
=100
故答案为:×
【点睛】本题考查数和形中的找规律问题。找到共同特征解决问题即可。
20.×
【分析】扇形统计图主要表示部分与部分之间,部分与总体之间的数量关系,以及各部分量占总体的百分比情况,要具体的数量选择条形统计图更加合适,据此解答。
【详解】条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;因此要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制条形统计图。
故答案为:×
【点睛】根据统计图的特征选择合适的统计图是解答题目的关键。
21.×
【分析】如图所示,横向表示所用时间,竖向表示行走的行程,行程相同的情况下,线段越陡的速度越快。
【详解】通过观察可知,小明步行600米所用时间是5分钟,小敏步行600米所用时间是6分钟。
故答案为:×
【点睛】解答本题需要明确折线统计图自身的特点,例如横轴、纵轴所代表的含义,并能够利用现有信息进行计算,从而求解。【来源:21cnj*y.co*m】
22.16部分;5051部分
【分析】要使得分成的份数尽可能多,就要求直线的交点尽可能多,新增加的直线必须和每一条直线都相交,如图,给出比较简单的情况,0条直线,可以分成1部分,1条直线,可以分成2部分,2条直线,可以分成4部分,每一次增加的份数是连续的自然数列。
【详解】如图所示:
假设用ak表示k条直线最多能把圆的内部分成的部分数,这里k=0,1,2,…
a0=1
a1=a0+1=2
a2=a1+2=4
a3=a2+3=7
a4=a3+4=11
…
答:5条直线可以把圆分成16部分;100条直线可以把圆分成5051部分。
【点睛】本题考查的是归纳递推计数问题,n条直线最多能把圆的内部分成部分。
23.51个
【分析】第1个正方体中有0个直角三角形;第2个正方体中有4个直角三角形;第3个正方体中有8个直角三角形;第4个正方体中有12个直角三角形。由此得出规律,三角形的个数都是4的倍数,然后得出假设第n个正方体,就有(n-1)×4个直角三角形。
【详解】根据图中的数据可得:1个正方形有0个三角形,可以写成(1-1)×4个;
2个正方形有4个三角形,可以写成(2-1)×4个;
3个正方形有8个三角形,可以写成(3-1)×4个;
4个正方形有12个三角形,可以写成(4-1)×4个;
所以当正方形的个数为a时,三角形的个数可以写成:(a-1)×4个;
设需要画a个正方形才得到200个直角三角形,则根据上面的结论可得:
(a-1)×4=200
a-1=200÷4
a-1=50
a=51
答:应画51个正方形。
【点睛】本题的关键是根据图形发现规律:第1个正方体就有0×4个直角三角形;第2个正方体就有(2-1)×4个直角三角形,然后以此类推。2·1·c·n·j·y
24.19个
【分析】每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。21*cnjy*com
【详解】首先每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。如果和是0出现,那么必然有另外一个数字不能出现。如果0出现在行的和中,说明有1行全是0,意味着列的和中至多出现0到9,加上行的和至多出现10个数字,所以少了一种可能。如果0出现在列的和中,说明在行的和中19不可能出现,所以0出现就意味着另一个数字不能出现,所以至多是19。如下图所示:【出处:21教育名师】
除去重复的和,所以和最多是19个。
答: 最多能得到19个不同的和数。
【点睛】我们先弄清楚题意,分行分列的分别求出和,最后算出不同和的个数,综合考虑此题中最小和是0,最大和是19。假设每一行全写0则和是0,写上1个1则和是1,以此类推可得出最多的和的个数是19个。【来源:21·世纪·教育·网】
25.45根
【详解】9×(9+1)÷2 = 45(根)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
