人教八上培优练:第06课 三角形全等的判定2(SAS)
文档属性
| 名称 | 人教八上培优练:第06课 三角形全等的判定2(SAS) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 12:28:50 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第06课 三角形全等的判定2(SAS)
题组A 基础过关练
1.下列选项可用SAS证明△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠B=∠B′,AC=A′C′ B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′ D.AC=A′C′,BC=B′C′,∠B=∠B′
2.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,
∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
3.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使,然后在BC的延长线上确定D,使,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS B.SAS C.ASA D.SSS
4.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
5.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.60° B.65° C.70° D.75°
6.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
7.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
8. 命题:如图,已知,共线,(1),那么.
(1)从①和②两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);
(2)根据你选择的条件,判定的方法是________;
(3)根据你选择的条件,完成的证明.
9.如图,已知AB=CD,AB∥CD,E、F是AC上两点,且AF=CE,连接BC,
求证:∠ABE=∠D.
10.已知:如图,△ABC中,∠ABC=70°,点D,E分别在AB,AC上,BD=BC,连接BE,将线段BE绕点B按逆时针方向旋转70°得到线段BF,连接DF.求证:△BCE≌△BDF.
题组B 能力提升练
1. 如图,点P是∠BAC平分线AD上的一点,AC=9,AB=5,PB=3,则PC的长可能是( )
A.6 B.7 C.8 D.9
2.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EFB=40°;④AD=AC,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.如图所示,,,,,,则( )
A. B. C. D.无法计算
4.如图,在△ABC中,∠B=110°,延长BC至点D使CD=AB,过点C作CE∥AB且使CE=BC,连接DE并延长DE交AC于点F,交AB于点H.若∠D=20°,则∠CFE的度数为______度.
5.如图,与中,,,,交于D.给出下列结论:
①;②;③;④.
其中正确的结论是__________(填写所有正确结论的序号).
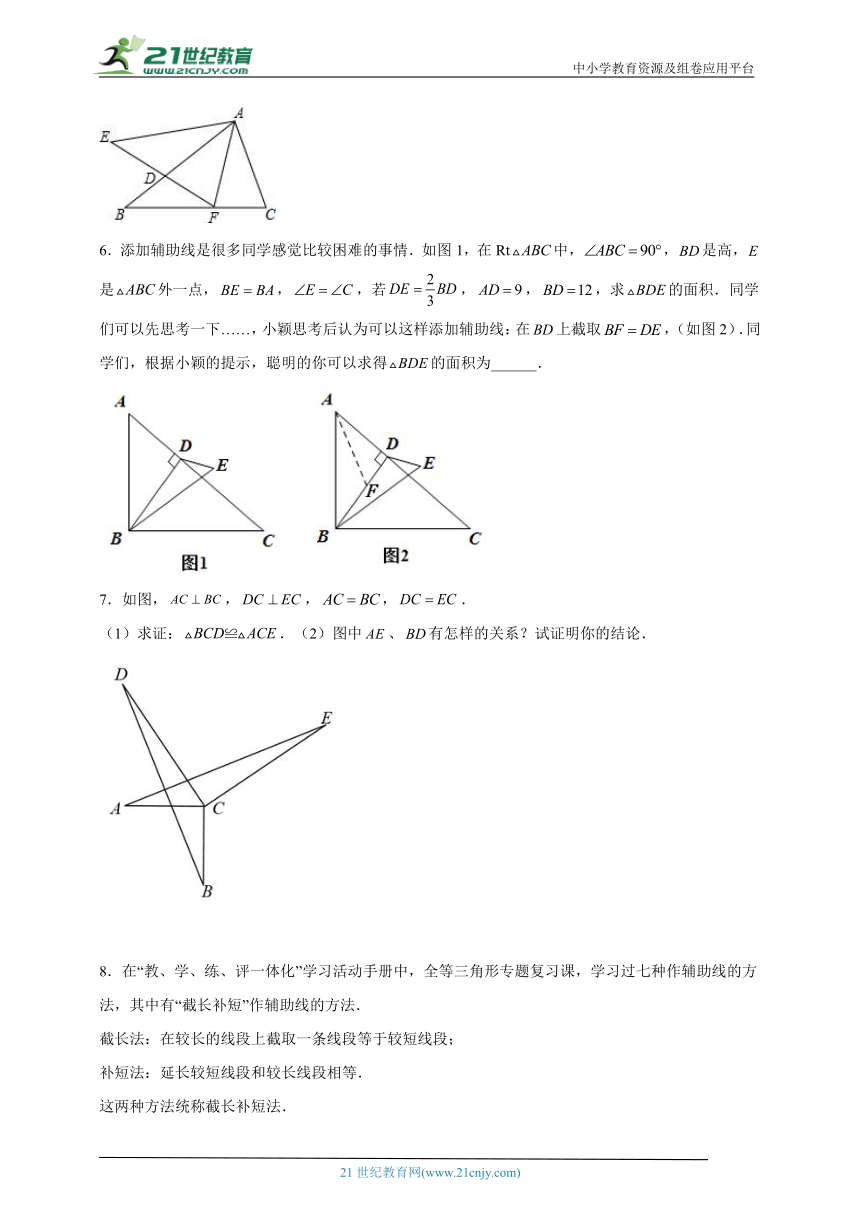
6.添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt中,,是高,是外一点,,,若,,,求的面积.同学们可以先思考一下……,小颖思考后认为可以这样添加辅助线:在上截取,(如图2).同学们,根据小颖的提示,聪明的你可以求得的面积为______.
7.如图,,,,.
(1)求证:.(2)图中、有怎样的关系?试证明你的结论.
8.在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1 = ∠2,P为AD上任一点,
求证:AB-AC>PB-PC
9. 为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.
题组C 培优拔尖练
1.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F,若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
2.如图,是的中线,E,F分别是和延长线上的点,且,连接.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=NBC=∠90°,连接MN,已知MN=4,则BD=_________.
4.如图,正方形ABCD的边长为4,点E、F分别在边AB、BC上,∠EDF=45°,
当AE=a,CF=b时,EF=_______(用含a、b的式子表示).
5.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
求证:CF=FG+CE.
6.已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)如图1,若∠DAB=60°,则∠AFG= ;
(2)如图2,若∠DAB=90°,则∠AFG= ;
(3)如图3,若∠DAB=,试探究∠AFG与的数量关系,并给予证明.
7.如图在△ABC和△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE交于点M.
(1)如图1,当点B,C,D在同一条直线上,且∠ACB=∠DCE=45°时,可以得到图中的一对全等三角形,即____________;
(2)当点D不在直线BC上时,如图2位置,且∠ACB=∠DCE=α.
①试说明AD=BE;②直接写出∠EMD的大小(用含α的代数式表示).
8.(1)如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.某同学做了如下探究,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应该是______.
(2)如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否依然成立?若成立,请说明理由;若不成立,写出正确的结论,并说明理由.
(3)如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
题组A 基础过关练
1.下列选项可用SAS证明△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠B=∠B′,AC=A′C′ B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′ D.AC=A′C′,BC=B′C′,∠B=∠B′
【答案】C
【分析】根据全等三角形SAS的判定逐项判定即可.
【详解】解:A、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
B、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
C、满足SAS,能证明△ABC≌△A′B′C′,符合题意;
D、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意,故选:C.
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定条件是解答的关键.
2.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
【分析】先由∠1=∠2=120°推导出∠ADC=∠AEB,再证明△ACD≌△ABE,则∠CAD=∠BAE=60°,再求出∠C的度数,进而求出∠CAE的度数.
【解答】解:如图,∵∠1=∠2=110°,∴180°﹣∠1=180°﹣∠2,
∵∠ADC=∠180°﹣∠1,∠AEB=180°﹣∠2,∴∠ADC=∠AEB,
在△ACD和△ABE中,,∴△ACD≌△ABE(SAS),
∴∠CAD=∠BAE=60°,∴∠C=∠1﹣∠CAD=110°﹣60°=50°,
∴∠CAE=180°﹣∠2﹣∠C=180°﹣110°﹣50°=20°,∴∠CAE的度数为20°,故选:D.
【点评】此题考查三角形的内角和定理及其推论、全等三角形的判定与性质等知识,证明△ACD≌△ABE是解题的关键.
3.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使,然后在BC的延长线上确定D,使,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS B.SAS C.ASA D.SSS
【答案】B
【分析】根据SAS即可证明△ACB≌△ACD,由此即可解决问题.
【详解】解:∵AC⊥BD,∴∠ACB=∠ACD=90°,
在△ACB和△ACD中,,
∴△ACB≌△ACD(SAS),∴AB=AD,故选:B.
【点睛】本题考查全等三角形的应用,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.
4.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
【答案】D
【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系:三角形两边之和大于第三边,两边之差小于第三边即可求解.
【详解】解:延长AD至E,使DE=AD,连接CE.
∵AD是边BC的中线,∴BD=CD,
在△ABD和△ECD中,
∴△ABD≌△ECD(SAS),∴CE=AB=7.
在△ACE中,CE﹣AC<AE<CE+AC,
即:2<2AD<12,1<AD<6.故选:D.
【点睛】此题主要考查了全等三角形的判定和性质、三角形的三边关系.注意:出现中点的辅助线一般应延长中线所在的直线构造全等三角形,这是一种非常重要的方法,要注意掌握.
5.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.60° B.65° C.70° D.75°
【答案】B
【分析】首先证明△DBE≌△ECF,进而得到∠EFC=∠DEB,再根据三角形内角和计算出∠CFE+∠FEC的度数,进而得到∠DEB+∠FEC的度数,然后可算出∠DEF的度数.
【详解】解:∵AB=AC,∴∠B=∠C,
在△DBE和△ECF中,,
∴△DBE≌△ECF(SAS),∴∠EFC=∠DEB,
∵∠A=50°,∴∠C=(180° 50°)÷2=65°,
∴∠CFE+∠FEC=180° 65°=115°,∴∠DEB+∠FEC=115°,
∴∠DEF=180° 115°=65°,故选:B.
【点睛】本题考查了全等三角形的性质和判定,三角形内角和定理,关键是掌握三角形内角和是180°.
6.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
【答案】①②④③,①④③②.
【分析】根据已知条件,根据三角形全等的判定方法,结合条件在图形上的位置进行选择能够判定三角形全等的条件,另一个作为结论,可得答案.
【解析】解:(1)①②④ ③.证明如下:∵DE=DC,DA=DB,AC=BE
∴△DCA≌△DEB(SSS)∴∠C=∠E(全等三角形的对应角相等)
(2) ①④③ ② 证明如下:∵,,
∴△DCA≌△DEB(SAS)∴DA=DB(全等三角形的对应边相等)故答案为:①②④ ③,①④③ ②.
【点睛】本题考查了全等三角形的判定与性质;这是一道考查三角形全等的识别方法的开放性题目,答案可有多种,结合图形与判定方法进行选择是解答本题的关键.
7.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
【分析】根据中点定义求出OA=OB,OC=OD,然后利用“边角边”证明△AOD和△BOC全等,根据全等三角形对应边相等即可证明.
【解答】解:∵O是AB、CD的中点,∴OA=OB,OC=OD,
在△AOD和△BOC中,,∴△AOD≌△BOC(SAS),∴CB=AD,
∵AD=35cm,∴CB=35(cm),答:CB的长度为35cm.
【点评】本题考查了全等三角形的应用,证明得到三角形全等是解题的关键.
8.命题:如图,已知,共线,(1),那么.
(1)从①和②两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);
(2)根据你选择的条件,判定的方法是________;
(3)根据你选择的条件,完成的证明.
【答案】(1)① (2)SAS (3)见解析
【分析】(1)根据全等三角形的判定方法分析得出答案;
(2)根据(1)直接填写即可;(3)利用SAS进行证明.
【解析】 (1)解:∵,∴∠A=∠F,
∵AC=EF,∴当时,可根据SAS证明;
当时,不能证明,故答案为:①;
(2)解:当时,可根据SAS证明,故答案为:SAS;
(3)证明:在△ABC和△FDE中,,∴.
【点睛】此题考查了添加条件证明两个三角形全等,正确掌握全等三角形的判定定理是解题的关键.
9.如图,已知AB=CD,AB∥CD,E、F是AC上两点,且AF=CE,连接BC,求证:∠ABE=∠D.
【分析】证明△ABE≌△CDF(SAS),由全等三角形的性质得出∠ABE=∠D.
【解答】证明:∵AB∥CD,∴∠A=∠DCF,
∵AF=CE,∴AF﹣EF=CE﹣EF,即AE=CF,
在△ABE和△CDF中,,∴△ABE≌△CDF(SAS),∴∠ABE=∠D.
【点评】本题考查了全等三角形的判定和性质,平行线的性质,熟练掌握全等三角形的判定是本题的关键.
10.已知:如图,△ABC中,∠ABC=70°,点D,E分别在AB,AC上,BD=BC,连接BE,将线段BE绕点B按逆时针方向旋转70°得到线段BF,连接DF.求证:△BCE≌△BDF.
【答案】见解析
【分析】由旋转得出BE=BF,∠EBF=70°,进而得出∠DBF=∠CBE,根据SAS即可证明△BCE≌△BDF.
【详解】∵将线段BE绕点B按逆时针方向旋转70°得到线段BF,∴BE=BF,∠EBF=70°,
∵∠ABC=70°,∴∠EBF=∠ABC,∴∠DBF=70°-∠ABE=∠CBE,
在△BCE和△BDF,∴△BCE≌△BDF(SAS).
【点睛】本题考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.
题组B 能力提升练
1. 如图,点P是∠BAC平分线AD上的一点,AC=9,AB=5,PB=3,则PC的长可能是( )
A.6 B.7 C.8 D.9
【分析】在AC上取AE=AB=5,然后证明△AEP﹣ABP,根据全等三角形对应边相等得到PE=PB=3,再根据三角形的任意两边之差小于第三边即可求解.
【解答】解:在AC上截取AE=AB=5,连接PE,
∵AC=9,∴CE=AC﹣AE=9﹣5=4,
∵点P是∠BAC平分线AD上的一点,∴∠CAD=∠BAD,
在△APE和△APB中,,∴△APE≌△APB(SAS),∴PE=PB=3,
∵4﹣3<PC<4+3,解得1<PC<7,∴PC取6,故选:A.
【点评】本题主要考查了全等三角形的判定与性质、三角形的三边关系;通过作辅助线构造全等三角形是解题的关键﹒
2.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EFB=40°;④AD=AC,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】由“SAS”可证△ABC≌△AEF,由全等三角形的性质依次判断可求解.
【详解】解:在△ABC和△AEF中,
,∴△ABC≌△AEF(SAS),
∴AF=AC,∠EAF=∠BAC,∠AFE=∠C,故②正确,
∴∠BAE=∠FAC=40°,故①正确,
∵∠AFB=∠C+∠FAC=∠AFE+∠EFB,
∴∠EFB=∠FAC=40°,故③正确,
无法证明AD=AC,故④错误,故选:C.
【点睛】本题考查全等三角形的判定与性质,是重要考点,掌握相关知识是解题关键.
3.如图所示,,,,,,则( )
A. B. C. D.无法计算
【答案】B
【分析】根据,可得,由证得与全等,得到,根据三角形外角和即可求解.
【详解】,
,即,
在与中,
≌,,
,,
,.故选:B.
【点睛】本题考查了全等三角形的判定和性质,三角形外角性质,推出≌是解题的关键.
4.如图,在△ABC中,∠B=110°,延长BC至点D使CD=AB,过点C作CE∥AB且使CE=BC,连接DE并延长DE交AC于点F,交AB于点H.若∠D=20°,则∠CFE的度数为______度.
【答案】30
【分析】证明△ABC≌△DCE,可得∠A=∠D= 20°,然后利用三角形内角和可得∠DEC=∠ACB= 50°,进而可以解决问题.
【详解】解:∵CE∥AB,∴∠B=∠DCE,
在△ABC与△DCE中,
,∴△ABC≌△DCE(SAS),
∴∠A=∠D=20°,∠DEC=∠ACB,
∵∠B=110°,∴∠ACB=180°﹣∠B+∠A=50°,
∴∠DEC=∠ACB=50°,
∵CE∥AB,∴∠BHF=∠DEC=50°,
∴∠CFE=∠AFH=∠BHF﹣∠A=50°﹣20°=30°.故答案为:30.
【点睛】本题考查了全等三角形的判定与性质,解决本题的关键是得到△ABC≌△DCE.
5.如图,与中,,,,交于D.给出下列结论:
①;②;③;④.
其中正确的结论是__________(填写所有正确结论的序号).
【答案】①③④
【分析】先根据三角形全等的判定定理与性质可得,再根据等腰三角形的性质即可得;先根据三角形全等的性质可得,由判断①、③;②假设,根据三角形全等的判定定理与性质可得,由此可得假设不成立;先根据三角形的外角性质可得,再根据角的和差可得,由此即可得④是否成立.
【详解】在和中,,
,
,
,则结论①正确;
∴,则结论③正确;
由三角形的外角性质得:,
又,
,则结论④正确;
假设,
在和中,,
,
,即AF是的角平分线,
∵AF不一定是的角平分线,
∴假设不一定成立,则结论②错误;
综上,正确的结论是①③④,故答案为:①③④.
【点睛】本题考查了三角形全等的判定定理与性质、等腰三角形的性质、三角形的外角性质、角平分线的定义等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.
6.添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt中,,是高,是外一点,,,若,,,求的面积.同学们可以先思考一下……,小颖思考后认为可以这样添加辅助线:在上截取,(如图2).同学们,根据小颖的提示,聪明的你可以求得的面积为______.
【答案】36
【分析】先通过等量代换推出,再利用“边角边”证明,再通过求出的面积即可.
【详解】解:是的高,
,
,
,
,
,
,
.
在和中,
,
,
.
,,,
,
,
.
故答案为:36.
【点睛】本题考查了全等三角形的判定和性质,根据题中所给提示,通过证明三角形全等,将求的面积转化为求的面积是解题的关键.
7.如图,,,,.
(1)求证:.(2)图中、有怎样的关系?试证明你的结论.
【答案】(1)证明见解析(2),,理由见解析
【分析】(1)根据,并结合图形可推出,再根据,,结论即可得证;
(2)如图,设交于点,交于点,由(1)的结论可推出,,由,,可得出,可得,由此即可解决问题.
(1)证明:∵,,∴,∴,∴,在和中,,∴.
(2)解:结论:,.理由如下:如图,设交于点,交于点,∵,∴,,∵,,∴,∴,∴.
【点睛】本题考查全等三角形的判定和性质,直角三角形的两锐角互余,三角形的内角和定理,垂直的定义.解题的关键是正确寻找判定三角形全等的条件,灵活运用所学知识解决问题.
8.在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1 = ∠2,P为AD上任一点,求证:AB-AC>PB-PC
【答案】见解析
【分析】截长法:在AB上截取AN=AC,连结PN,可证得△APN≌△APC,可得到PC=PN,△BPN中,利用三角形的三边关系,即可求证;补短法:延长AC至M,使AM=AB,连结PM,证明△ABP≌△AMP,可得PB=PM,在△PCM中,利用三角形的三边关系,即可求证.
【详解】解:截长法:在AB上截取AN=AC,连结PN,
在△APN和△APC中
∵AN=AC,∠1=∠2,AP=AP,
∴△APN≌△APC,
∴PC=PN,
∵△BPN中有PB-PN<BN,
即PB-PC<AB-AC;
补短法:延长AC至M,使AM=AB,连结PM,
在△ABP和△AMP中,∵AB=AM,∠1=∠2,AP=AP,
∴△ABP≌△AMP,∴PB=PM,
又∵在△PCM中有CM>PM-PC,即AB-AC>PB-PC.
【点睛】本题主要考查了全等三角形的判定和性质,三角形的三边关系,理解截长补短法是解题的关键.
9. 为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.
【分析】甲同学作出的是全等三角形,然后根据全等三角形对应边相等测量的,所以是可行的;
甲同学利用的是“边角边”,乙同学的方案根据等腰三角形的性质得出AB=BC,故方案可行.
【解答】解:甲、乙两同学的方案都可行,
甲同学方案:在△ABO和△CDO中,,∴△ABO≌△CDO(SAS),∴AB=CD;
乙同学方案:∵AD=CD,DB⊥AC于点B,∴AB=BC,
∴测量出线段BC的长度就是池塘两端A,B之间的距离,∴甲、乙两同学的方案都可行.
【点评】本题主要考查了全等三角形的应用,熟练掌握全等三角形判定的“SAS”定理是解决问题的关键
题组C 培优拔尖练
1.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F,若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
【答案】C
【分析】由△ABE≌△BCD(SAS),可求出∠BAE=∠CBD=21°,△ABC是等腰三角形,BF是底边AC的高,可以求出∠DBF=90°﹣(∠CBD+∠C).
【详解】在△ABE和△BCD中,
,∴△ABE≌△BCD(SAS),∴∠BAE=∠CBD,
∵∠BAE=21°,∠C=28°,∴∠CBD=21°,
∴∠BDF=∠CBD+∠C=21°+28°=49°,
∵BF⊥AC,∴∠BFD=90°,
∴∠FBD=90°﹣∠BDF=90°﹣49°=41°故选:C.
【点睛】本题考查了全等三角形和等腰三角形的性质,此类题型比较灵活,但围绕的知识点是固定的,解题时注意结合图形寻找已知条件与问题之间的位置关系,把条件与问题的联系作为主要的思考方向.
2.如图,是的中线,E,F分别是和延长线上的点,且,连接.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】根据三角形中线的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:是的中线,,
在和中,,,故④正确
,,故①正确,
,故③正确,
,点到、的距离相等,
和面积相等,故②正确,
综上所述,正确的有4个,故选:D.
【点睛】本题考查了全等三角形的判定与性质,等底等高的三角形的面积相等,解题的关键是熟练掌握三角形全等的判定方法并准确识图.
3.如图,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=NBC=∠90°,连接MN,已知MN=4,则BD=_________.
【答案】2
【分析】延长BD到E,使DE=BD,连接AE,证明△ADE≌△CDB(SAS),可得AE=CB,∠EAD=∠BCD,再根据△ABM和△BCN是等腰直角三角形,证明△MBN≌△BAE,可得MN=BE,进而可得BD与MN的数量关系即可求解.
【详解】解:如图,延长BD到E,使DE=BD,连接AE,
∵点D是AC的中点,∴AD=CD,
在△ADE和△CDB中,,∴△ADE≌△CDB(SAS),
∴AE=CB,∠EAD=∠BCD,
∵△ABM和△BCN是等腰直角三角形,
∴AB=BM,CB=NB,∠ABM=∠CBN=90°,∴BN=AE,
又∠MBN+∠ABC=360°-90°-90°=180°,
∵∠BCA+∠BAC+∠ABC=180°,
∴∠MBN=∠BCA+∠BAC=∠EAD+∠BAC=∠BAE,
在△MBN和△BAE中,,∴△MBN≌△BAE(SAS),∴MN=BE,
∵BE=2BD,∴MN=2BD.又MN=4,∴BD=2,故答案为:2.
【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形,解决本题的关键是掌握全等三角形的判定与性质.
4.如图,正方形ABCD的边长为4,点E、F分别在边AB、BC上,∠EDF=45°,当AE=a,CF=b时,EF=_______(用含a、b的式子表示).
【答案】a+b##b+a
【分析】延长FC到M,使CM=AE,连接DM,通过SAS可证明△ADE≌△CDM,得DE=DM,∠ADE=∠CDM,再通过SAS证明△DEF≌△DMF,从而有EF=MF=a+b.
【详解】解:延长FC到M,使CM=AE,连接DM,
∵四边形ABCD是正方形,∴AD=CD,∠A=∠DCM=90°,
在△ADE和△CDM中,,
∴△ADE≌△CDM(SAS),
∴DE=DM,∠ADE=∠CDM,
∵∠EDF=45°,∴∠ADE+∠FDC=45°,
∴∠CDM+∠FDC=45°,∴∠FDM=∠EDF=45°,
在△DEF与△DMF中,,
∴△DEF≌△DMF(SAS),∴EF=MF=a+b,故答案为:a+b.
【点睛】本题主要考查了全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.
5.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
求证:CF=FG+CE.
【答案】见解析
【分析】在BC上取点M,使CM=CE,证明△CDE≌△CDM(SAS),可得DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,证明∠BDM=180°-∠ABC-∠DMB=180°-∠ABC-∠AEB=∠A,然后证明△DGF≌△DMF(SAS),可得GF=MF,进而可以解决问题.
【详解】证明:如图,在BC上取点M,使CM=CE,
∵CD平分∠ACB,∴∠ACD=∠BCD,
在△CDE和△CDM中,,∴△CDE≌△CDM(SAS),
∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,
∵GD=DE, ∴GD=MD,
∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,
∵BE平分∠ABC,∴∠ABE=∠CBE=∠ABC,
∴∠BDM=180°-∠ABC-∠DMB=180°-∠ABC-∠AEB=∠A,
∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠FDG,
在△DGF和△DMF中,∵,
∴△DGF≌△DMF(SAS),∴GF=MF,
∴CF=CM+FM=CE+GF.∴CF=FG+CE.
【点睛】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.
6.已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)如图1,若∠DAB=60°,则∠AFG= ;
(2)如图2,若∠DAB=90°,则∠AFG= ;
(3)如图3,若∠DAB=,试探究∠AFG与的数量关系,并给予证明.
【答案】(1)60°(2)45°(3)(180°﹣),证明见解析
【分析】(1)连接AG.易证△ADC≌△ABE,可得DC=BE,∠ADC=∠ABE,AD=AB,根据G、F分别是DC与BE的中点,可得DG=BF,即可证明△ADG≌△ABF,可得AG=AF,∠DAG=∠BAF,即可求得∠DAB=∠GAF,即可解题.
(2)根据(1)中结论即可求得∠AFG的值,即可解题;
(3)根据(1)中结论即可求得∠AFG的值,即可解题.
(1)连接AG.
∵∠DAB=∠CAE,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE.
在△ADC和△ABE中,,
∴△ADC≌△ABE(SAS),∴DC=BE,∠ADC=∠ABE.
∵G、F分别是DC与BE的中点,
∴DGDC,BFBE,∴DG=BF.
在△ADG和△ABF中,,
∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,
∴∠AGF=∠AFG,∠DAG﹣∠BAG=∠BAF﹣∠BAG,∴∠DAB=∠GAF.
∵∠DAB=60°,∴∠GAF=60°.
∵∠GAF+∠AFG+∠AGF=180°,∴∠AFG=60°;故答案为 60°,
(2)连接AG,如图2,
∵∠DAB=90°,∠DAB=∠GAF,(已证)∴∠GAF=90°,
∵AG=AF,∴∠AFG×(180°﹣90°)=45°;故答案为 45°,
(3)连接AG,如图3,
∵∠DAB=α,∠DAB=∠GAF,(已证)∴∠GAF=α,
∵AG=AF,∴∠AFG(180°﹣α).
【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADC≌△ABE和△ADG≌△ABF是解题的关键.
7.如图在△ABC和△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE交于点M.
(1)如图1,当点B,C,D在同一条直线上,且∠ACB=∠DCE=45°时,可以得到图中的一对全等三角形,即____________;(2)当点D不在直线BC上时,如图2位置,且∠ACB=∠DCE=α.
①试说明AD=BE;②直接写出∠EMD的大小(用含α的代数式表示).
【答案】(1)△BCE,△ACD(2)①见解析;②∠EMD=α.
【分析】(1)由“SAS”可证△BCE≌△ACD;(2)①由“SAS”可证△BCE≌△ACD,可得AD=BE,
②由全等三角形的性质可得∠CAD=∠CBE,由三角形的内角和定理可求解.
(1)解:∵∠ACB=∠DCE=45°,∴∠ACD=∠BCE,在△BCE和△ACD中,,∴△BCE≌△ACD(SAS),故答案为:△BCE,△ACD;
(2)①证明:∵∠ACB=∠DCE=α,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE;②解:∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠BAC+∠ABC=180°-α,∴∠BAM+∠ABM=180°-α,∴∠AMB=∠EMD=180°-(180°-α)=α.
【点睛】本题考查了全等三角形的判定和性质,证明△ACD≌△BCE是解题的关键.
8.(1)如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.某同学做了如下探究,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应该是______.
(2)如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否依然成立?若成立,请说明理由;若不成立,写出正确的结论,并说明理由.
(3)如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【答案】(1)EF=BE+DF;(2)结论EF=BE+DF仍然成立;理由见解析;(3)此时两舰艇之间的距离是210海里
【分析】(1)根据题意证明△ABE≌△ADG,△AEF≌△AGF,可得EF=FG,根据FG=DG+DF=BE+DF,可得EF=BE+DF;(2)延长FD到点G.使DG=BE.连结AG,同(1)的方法证明即可;
(3)连接EF,延长AE、BF相交于点C,应用(2)的结论可得EF=AE+BF进而气得的长,即两舰艇之间的距离
【详解】(1)EF=BE+DF,证明如下:
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△AGF中,,
∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+DF,∴EF=BE+DF;故答案为 EF=BE+DF.
(2)结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连结AG,如图②,
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,∴∠EAF=∠GAF,
在△AEF和△AGF中,
,∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+DF,∴EF=BE+DF;
(3)如图③,连接EF,延长AE、BF相交于点C,
∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EOF=∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,∴结论EF=AE+BF成立,
即EF=1.5×(60+80)=210海里.
答:此时两舰艇之间的距离是210海里.
【点睛】本题考查全等三角形的性质与判定,方位角的计算,掌握全等三角形的性质与判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第06课 三角形全等的判定2(SAS)
题组A 基础过关练
1.下列选项可用SAS证明△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠B=∠B′,AC=A′C′ B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′ D.AC=A′C′,BC=B′C′,∠B=∠B′
2.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,
∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
3.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使,然后在BC的延长线上确定D,使,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS B.SAS C.ASA D.SSS
4.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
5.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.60° B.65° C.70° D.75°
6.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
7.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
8. 命题:如图,已知,共线,(1),那么.
(1)从①和②两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);
(2)根据你选择的条件,判定的方法是________;
(3)根据你选择的条件,完成的证明.
9.如图,已知AB=CD,AB∥CD,E、F是AC上两点,且AF=CE,连接BC,
求证:∠ABE=∠D.
10.已知:如图,△ABC中,∠ABC=70°,点D,E分别在AB,AC上,BD=BC,连接BE,将线段BE绕点B按逆时针方向旋转70°得到线段BF,连接DF.求证:△BCE≌△BDF.
题组B 能力提升练
1. 如图,点P是∠BAC平分线AD上的一点,AC=9,AB=5,PB=3,则PC的长可能是( )
A.6 B.7 C.8 D.9
2.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EFB=40°;④AD=AC,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.如图所示,,,,,,则( )
A. B. C. D.无法计算
4.如图,在△ABC中,∠B=110°,延长BC至点D使CD=AB,过点C作CE∥AB且使CE=BC,连接DE并延长DE交AC于点F,交AB于点H.若∠D=20°,则∠CFE的度数为______度.
5.如图,与中,,,,交于D.给出下列结论:
①;②;③;④.
其中正确的结论是__________(填写所有正确结论的序号).
6.添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt中,,是高,是外一点,,,若,,,求的面积.同学们可以先思考一下……,小颖思考后认为可以这样添加辅助线:在上截取,(如图2).同学们,根据小颖的提示,聪明的你可以求得的面积为______.
7.如图,,,,.
(1)求证:.(2)图中、有怎样的关系?试证明你的结论.
8.在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1 = ∠2,P为AD上任一点,
求证:AB-AC>PB-PC
9. 为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.
题组C 培优拔尖练
1.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F,若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
2.如图,是的中线,E,F分别是和延长线上的点,且,连接.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=NBC=∠90°,连接MN,已知MN=4,则BD=_________.
4.如图,正方形ABCD的边长为4,点E、F分别在边AB、BC上,∠EDF=45°,
当AE=a,CF=b时,EF=_______(用含a、b的式子表示).
5.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
求证:CF=FG+CE.
6.已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)如图1,若∠DAB=60°,则∠AFG= ;
(2)如图2,若∠DAB=90°,则∠AFG= ;
(3)如图3,若∠DAB=,试探究∠AFG与的数量关系,并给予证明.
7.如图在△ABC和△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE交于点M.
(1)如图1,当点B,C,D在同一条直线上,且∠ACB=∠DCE=45°时,可以得到图中的一对全等三角形,即____________;
(2)当点D不在直线BC上时,如图2位置,且∠ACB=∠DCE=α.
①试说明AD=BE;②直接写出∠EMD的大小(用含α的代数式表示).
8.(1)如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.某同学做了如下探究,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应该是______.
(2)如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否依然成立?若成立,请说明理由;若不成立,写出正确的结论,并说明理由.
(3)如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
题组A 基础过关练
1.下列选项可用SAS证明△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠B=∠B′,AC=A′C′ B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′ D.AC=A′C′,BC=B′C′,∠B=∠B′
【答案】C
【分析】根据全等三角形SAS的判定逐项判定即可.
【详解】解:A、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
B、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意;
C、满足SAS,能证明△ABC≌△A′B′C′,符合题意;
D、不满足SAS,不能证明△ABC≌△A′B′C′,不符合题意,故选:C.
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定条件是解答的关键.
2.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
【分析】先由∠1=∠2=120°推导出∠ADC=∠AEB,再证明△ACD≌△ABE,则∠CAD=∠BAE=60°,再求出∠C的度数,进而求出∠CAE的度数.
【解答】解:如图,∵∠1=∠2=110°,∴180°﹣∠1=180°﹣∠2,
∵∠ADC=∠180°﹣∠1,∠AEB=180°﹣∠2,∴∠ADC=∠AEB,
在△ACD和△ABE中,,∴△ACD≌△ABE(SAS),
∴∠CAD=∠BAE=60°,∴∠C=∠1﹣∠CAD=110°﹣60°=50°,
∴∠CAE=180°﹣∠2﹣∠C=180°﹣110°﹣50°=20°,∴∠CAE的度数为20°,故选:D.
【点评】此题考查三角形的内角和定理及其推论、全等三角形的判定与性质等知识,证明△ACD≌△ABE是解题的关键.
3.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使,然后在BC的延长线上确定D,使,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS B.SAS C.ASA D.SSS
【答案】B
【分析】根据SAS即可证明△ACB≌△ACD,由此即可解决问题.
【详解】解:∵AC⊥BD,∴∠ACB=∠ACD=90°,
在△ACB和△ACD中,,
∴△ACB≌△ACD(SAS),∴AB=AD,故选:B.
【点睛】本题考查全等三角形的应用,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.
4.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
【答案】D
【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系:三角形两边之和大于第三边,两边之差小于第三边即可求解.
【详解】解:延长AD至E,使DE=AD,连接CE.
∵AD是边BC的中线,∴BD=CD,
在△ABD和△ECD中,
∴△ABD≌△ECD(SAS),∴CE=AB=7.
在△ACE中,CE﹣AC<AE<CE+AC,
即:2<2AD<12,1<AD<6.故选:D.
【点睛】此题主要考查了全等三角形的判定和性质、三角形的三边关系.注意:出现中点的辅助线一般应延长中线所在的直线构造全等三角形,这是一种非常重要的方法,要注意掌握.
5.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.60° B.65° C.70° D.75°
【答案】B
【分析】首先证明△DBE≌△ECF,进而得到∠EFC=∠DEB,再根据三角形内角和计算出∠CFE+∠FEC的度数,进而得到∠DEB+∠FEC的度数,然后可算出∠DEF的度数.
【详解】解:∵AB=AC,∴∠B=∠C,
在△DBE和△ECF中,,
∴△DBE≌△ECF(SAS),∴∠EFC=∠DEB,
∵∠A=50°,∴∠C=(180° 50°)÷2=65°,
∴∠CFE+∠FEC=180° 65°=115°,∴∠DEB+∠FEC=115°,
∴∠DEF=180° 115°=65°,故选:B.
【点睛】本题考查了全等三角形的性质和判定,三角形内角和定理,关键是掌握三角形内角和是180°.
6.如图,在与中,有以下四个等式①;②;③;④,请以其中三个等式作条件,余下一个作结论,写出所有的正确判断 ___________________________(用形式表示)
【答案】①②④③,①④③②.
【分析】根据已知条件,根据三角形全等的判定方法,结合条件在图形上的位置进行选择能够判定三角形全等的条件,另一个作为结论,可得答案.
【解析】解:(1)①②④ ③.证明如下:∵DE=DC,DA=DB,AC=BE
∴△DCA≌△DEB(SSS)∴∠C=∠E(全等三角形的对应角相等)
(2) ①④③ ② 证明如下:∵,,
∴△DCA≌△DEB(SAS)∴DA=DB(全等三角形的对应边相等)故答案为:①②④ ③,①④③ ②.
【点睛】本题考查了全等三角形的判定与性质;这是一道考查三角形全等的识别方法的开放性题目,答案可有多种,结合图形与判定方法进行选择是解答本题的关键.
7.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
【分析】根据中点定义求出OA=OB,OC=OD,然后利用“边角边”证明△AOD和△BOC全等,根据全等三角形对应边相等即可证明.
【解答】解:∵O是AB、CD的中点,∴OA=OB,OC=OD,
在△AOD和△BOC中,,∴△AOD≌△BOC(SAS),∴CB=AD,
∵AD=35cm,∴CB=35(cm),答:CB的长度为35cm.
【点评】本题考查了全等三角形的应用,证明得到三角形全等是解题的关键.
8.命题:如图,已知,共线,(1),那么.
(1)从①和②两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);
(2)根据你选择的条件,判定的方法是________;
(3)根据你选择的条件,完成的证明.
【答案】(1)① (2)SAS (3)见解析
【分析】(1)根据全等三角形的判定方法分析得出答案;
(2)根据(1)直接填写即可;(3)利用SAS进行证明.
【解析】 (1)解:∵,∴∠A=∠F,
∵AC=EF,∴当时,可根据SAS证明;
当时,不能证明,故答案为:①;
(2)解:当时,可根据SAS证明,故答案为:SAS;
(3)证明:在△ABC和△FDE中,,∴.
【点睛】此题考查了添加条件证明两个三角形全等,正确掌握全等三角形的判定定理是解题的关键.
9.如图,已知AB=CD,AB∥CD,E、F是AC上两点,且AF=CE,连接BC,求证:∠ABE=∠D.
【分析】证明△ABE≌△CDF(SAS),由全等三角形的性质得出∠ABE=∠D.
【解答】证明:∵AB∥CD,∴∠A=∠DCF,
∵AF=CE,∴AF﹣EF=CE﹣EF,即AE=CF,
在△ABE和△CDF中,,∴△ABE≌△CDF(SAS),∴∠ABE=∠D.
【点评】本题考查了全等三角形的判定和性质,平行线的性质,熟练掌握全等三角形的判定是本题的关键.
10.已知:如图,△ABC中,∠ABC=70°,点D,E分别在AB,AC上,BD=BC,连接BE,将线段BE绕点B按逆时针方向旋转70°得到线段BF,连接DF.求证:△BCE≌△BDF.
【答案】见解析
【分析】由旋转得出BE=BF,∠EBF=70°,进而得出∠DBF=∠CBE,根据SAS即可证明△BCE≌△BDF.
【详解】∵将线段BE绕点B按逆时针方向旋转70°得到线段BF,∴BE=BF,∠EBF=70°,
∵∠ABC=70°,∴∠EBF=∠ABC,∴∠DBF=70°-∠ABE=∠CBE,
在△BCE和△BDF,∴△BCE≌△BDF(SAS).
【点睛】本题考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.
题组B 能力提升练
1. 如图,点P是∠BAC平分线AD上的一点,AC=9,AB=5,PB=3,则PC的长可能是( )
A.6 B.7 C.8 D.9
【分析】在AC上取AE=AB=5,然后证明△AEP﹣ABP,根据全等三角形对应边相等得到PE=PB=3,再根据三角形的任意两边之差小于第三边即可求解.
【解答】解:在AC上截取AE=AB=5,连接PE,
∵AC=9,∴CE=AC﹣AE=9﹣5=4,
∵点P是∠BAC平分线AD上的一点,∴∠CAD=∠BAD,
在△APE和△APB中,,∴△APE≌△APB(SAS),∴PE=PB=3,
∵4﹣3<PC<4+3,解得1<PC<7,∴PC取6,故选:A.
【点评】本题主要考查了全等三角形的判定与性质、三角形的三边关系;通过作辅助线构造全等三角形是解题的关键﹒
2.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EFB=40°;④AD=AC,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】由“SAS”可证△ABC≌△AEF,由全等三角形的性质依次判断可求解.
【详解】解:在△ABC和△AEF中,
,∴△ABC≌△AEF(SAS),
∴AF=AC,∠EAF=∠BAC,∠AFE=∠C,故②正确,
∴∠BAE=∠FAC=40°,故①正确,
∵∠AFB=∠C+∠FAC=∠AFE+∠EFB,
∴∠EFB=∠FAC=40°,故③正确,
无法证明AD=AC,故④错误,故选:C.
【点睛】本题考查全等三角形的判定与性质,是重要考点,掌握相关知识是解题关键.
3.如图所示,,,,,,则( )
A. B. C. D.无法计算
【答案】B
【分析】根据,可得,由证得与全等,得到,根据三角形外角和即可求解.
【详解】,
,即,
在与中,
≌,,
,,
,.故选:B.
【点睛】本题考查了全等三角形的判定和性质,三角形外角性质,推出≌是解题的关键.
4.如图,在△ABC中,∠B=110°,延长BC至点D使CD=AB,过点C作CE∥AB且使CE=BC,连接DE并延长DE交AC于点F,交AB于点H.若∠D=20°,则∠CFE的度数为______度.
【答案】30
【分析】证明△ABC≌△DCE,可得∠A=∠D= 20°,然后利用三角形内角和可得∠DEC=∠ACB= 50°,进而可以解决问题.
【详解】解:∵CE∥AB,∴∠B=∠DCE,
在△ABC与△DCE中,
,∴△ABC≌△DCE(SAS),
∴∠A=∠D=20°,∠DEC=∠ACB,
∵∠B=110°,∴∠ACB=180°﹣∠B+∠A=50°,
∴∠DEC=∠ACB=50°,
∵CE∥AB,∴∠BHF=∠DEC=50°,
∴∠CFE=∠AFH=∠BHF﹣∠A=50°﹣20°=30°.故答案为:30.
【点睛】本题考查了全等三角形的判定与性质,解决本题的关键是得到△ABC≌△DCE.
5.如图,与中,,,,交于D.给出下列结论:
①;②;③;④.
其中正确的结论是__________(填写所有正确结论的序号).
【答案】①③④
【分析】先根据三角形全等的判定定理与性质可得,再根据等腰三角形的性质即可得;先根据三角形全等的性质可得,由判断①、③;②假设,根据三角形全等的判定定理与性质可得,由此可得假设不成立;先根据三角形的外角性质可得,再根据角的和差可得,由此即可得④是否成立.
【详解】在和中,,
,
,
,则结论①正确;
∴,则结论③正确;
由三角形的外角性质得:,
又,
,则结论④正确;
假设,
在和中,,
,
,即AF是的角平分线,
∵AF不一定是的角平分线,
∴假设不一定成立,则结论②错误;
综上,正确的结论是①③④,故答案为:①③④.
【点睛】本题考查了三角形全等的判定定理与性质、等腰三角形的性质、三角形的外角性质、角平分线的定义等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.
6.添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt中,,是高,是外一点,,,若,,,求的面积.同学们可以先思考一下……,小颖思考后认为可以这样添加辅助线:在上截取,(如图2).同学们,根据小颖的提示,聪明的你可以求得的面积为______.
【答案】36
【分析】先通过等量代换推出,再利用“边角边”证明,再通过求出的面积即可.
【详解】解:是的高,
,
,
,
,
,
,
.
在和中,
,
,
.
,,,
,
,
.
故答案为:36.
【点睛】本题考查了全等三角形的判定和性质,根据题中所给提示,通过证明三角形全等,将求的面积转化为求的面积是解题的关键.
7.如图,,,,.
(1)求证:.(2)图中、有怎样的关系?试证明你的结论.
【答案】(1)证明见解析(2),,理由见解析
【分析】(1)根据,并结合图形可推出,再根据,,结论即可得证;
(2)如图,设交于点,交于点,由(1)的结论可推出,,由,,可得出,可得,由此即可解决问题.
(1)证明:∵,,∴,∴,∴,在和中,,∴.
(2)解:结论:,.理由如下:如图,设交于点,交于点,∵,∴,,∵,,∴,∴,∴.
【点睛】本题考查全等三角形的判定和性质,直角三角形的两锐角互余,三角形的内角和定理,垂直的定义.解题的关键是正确寻找判定三角形全等的条件,灵活运用所学知识解决问题.
8.在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1 = ∠2,P为AD上任一点,求证:AB-AC>PB-PC
【答案】见解析
【分析】截长法:在AB上截取AN=AC,连结PN,可证得△APN≌△APC,可得到PC=PN,△BPN中,利用三角形的三边关系,即可求证;补短法:延长AC至M,使AM=AB,连结PM,证明△ABP≌△AMP,可得PB=PM,在△PCM中,利用三角形的三边关系,即可求证.
【详解】解:截长法:在AB上截取AN=AC,连结PN,
在△APN和△APC中
∵AN=AC,∠1=∠2,AP=AP,
∴△APN≌△APC,
∴PC=PN,
∵△BPN中有PB-PN<BN,
即PB-PC<AB-AC;
补短法:延长AC至M,使AM=AB,连结PM,
在△ABP和△AMP中,∵AB=AM,∠1=∠2,AP=AP,
∴△ABP≌△AMP,∴PB=PM,
又∵在△PCM中有CM>PM-PC,即AB-AC>PB-PC.
【点睛】本题主要考查了全等三角形的判定和性质,三角形的三边关系,理解截长补短法是解题的关键.
9. 为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可;
乙:如图2,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
甲、乙两个同学的方案是否可行?请说明理由.
【分析】甲同学作出的是全等三角形,然后根据全等三角形对应边相等测量的,所以是可行的;
甲同学利用的是“边角边”,乙同学的方案根据等腰三角形的性质得出AB=BC,故方案可行.
【解答】解:甲、乙两同学的方案都可行,
甲同学方案:在△ABO和△CDO中,,∴△ABO≌△CDO(SAS),∴AB=CD;
乙同学方案:∵AD=CD,DB⊥AC于点B,∴AB=BC,
∴测量出线段BC的长度就是池塘两端A,B之间的距离,∴甲、乙两同学的方案都可行.
【点评】本题主要考查了全等三角形的应用,熟练掌握全等三角形判定的“SAS”定理是解决问题的关键
题组C 培优拔尖练
1.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F,若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
【答案】C
【分析】由△ABE≌△BCD(SAS),可求出∠BAE=∠CBD=21°,△ABC是等腰三角形,BF是底边AC的高,可以求出∠DBF=90°﹣(∠CBD+∠C).
【详解】在△ABE和△BCD中,
,∴△ABE≌△BCD(SAS),∴∠BAE=∠CBD,
∵∠BAE=21°,∠C=28°,∴∠CBD=21°,
∴∠BDF=∠CBD+∠C=21°+28°=49°,
∵BF⊥AC,∴∠BFD=90°,
∴∠FBD=90°﹣∠BDF=90°﹣49°=41°故选:C.
【点睛】本题考查了全等三角形和等腰三角形的性质,此类题型比较灵活,但围绕的知识点是固定的,解题时注意结合图形寻找已知条件与问题之间的位置关系,把条件与问题的联系作为主要的思考方向.
2.如图,是的中线,E,F分别是和延长线上的点,且,连接.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】根据三角形中线的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:是的中线,,
在和中,,,故④正确
,,故①正确,
,故③正确,
,点到、的距离相等,
和面积相等,故②正确,
综上所述,正确的有4个,故选:D.
【点睛】本题考查了全等三角形的判定与性质,等底等高的三角形的面积相等,解题的关键是熟练掌握三角形全等的判定方法并准确识图.
3.如图,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=NBC=∠90°,连接MN,已知MN=4,则BD=_________.
【答案】2
【分析】延长BD到E,使DE=BD,连接AE,证明△ADE≌△CDB(SAS),可得AE=CB,∠EAD=∠BCD,再根据△ABM和△BCN是等腰直角三角形,证明△MBN≌△BAE,可得MN=BE,进而可得BD与MN的数量关系即可求解.
【详解】解:如图,延长BD到E,使DE=BD,连接AE,
∵点D是AC的中点,∴AD=CD,
在△ADE和△CDB中,,∴△ADE≌△CDB(SAS),
∴AE=CB,∠EAD=∠BCD,
∵△ABM和△BCN是等腰直角三角形,
∴AB=BM,CB=NB,∠ABM=∠CBN=90°,∴BN=AE,
又∠MBN+∠ABC=360°-90°-90°=180°,
∵∠BCA+∠BAC+∠ABC=180°,
∴∠MBN=∠BCA+∠BAC=∠EAD+∠BAC=∠BAE,
在△MBN和△BAE中,,∴△MBN≌△BAE(SAS),∴MN=BE,
∵BE=2BD,∴MN=2BD.又MN=4,∴BD=2,故答案为:2.
【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形,解决本题的关键是掌握全等三角形的判定与性质.
4.如图,正方形ABCD的边长为4,点E、F分别在边AB、BC上,∠EDF=45°,当AE=a,CF=b时,EF=_______(用含a、b的式子表示).
【答案】a+b##b+a
【分析】延长FC到M,使CM=AE,连接DM,通过SAS可证明△ADE≌△CDM,得DE=DM,∠ADE=∠CDM,再通过SAS证明△DEF≌△DMF,从而有EF=MF=a+b.
【详解】解:延长FC到M,使CM=AE,连接DM,
∵四边形ABCD是正方形,∴AD=CD,∠A=∠DCM=90°,
在△ADE和△CDM中,,
∴△ADE≌△CDM(SAS),
∴DE=DM,∠ADE=∠CDM,
∵∠EDF=45°,∴∠ADE+∠FDC=45°,
∴∠CDM+∠FDC=45°,∴∠FDM=∠EDF=45°,
在△DEF与△DMF中,,
∴△DEF≌△DMF(SAS),∴EF=MF=a+b,故答案为:a+b.
【点睛】本题主要考查了全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.
5.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
求证:CF=FG+CE.
【答案】见解析
【分析】在BC上取点M,使CM=CE,证明△CDE≌△CDM(SAS),可得DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,证明∠BDM=180°-∠ABC-∠DMB=180°-∠ABC-∠AEB=∠A,然后证明△DGF≌△DMF(SAS),可得GF=MF,进而可以解决问题.
【详解】证明:如图,在BC上取点M,使CM=CE,
∵CD平分∠ACB,∴∠ACD=∠BCD,
在△CDE和△CDM中,,∴△CDE≌△CDM(SAS),
∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,
∵GD=DE, ∴GD=MD,
∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,
∵BE平分∠ABC,∴∠ABE=∠CBE=∠ABC,
∴∠BDM=180°-∠ABC-∠DMB=180°-∠ABC-∠AEB=∠A,
∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠FDG,
在△DGF和△DMF中,∵,
∴△DGF≌△DMF(SAS),∴GF=MF,
∴CF=CM+FM=CE+GF.∴CF=FG+CE.
【点睛】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.
6.已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)如图1,若∠DAB=60°,则∠AFG= ;
(2)如图2,若∠DAB=90°,则∠AFG= ;
(3)如图3,若∠DAB=,试探究∠AFG与的数量关系,并给予证明.
【答案】(1)60°(2)45°(3)(180°﹣),证明见解析
【分析】(1)连接AG.易证△ADC≌△ABE,可得DC=BE,∠ADC=∠ABE,AD=AB,根据G、F分别是DC与BE的中点,可得DG=BF,即可证明△ADG≌△ABF,可得AG=AF,∠DAG=∠BAF,即可求得∠DAB=∠GAF,即可解题.
(2)根据(1)中结论即可求得∠AFG的值,即可解题;
(3)根据(1)中结论即可求得∠AFG的值,即可解题.
(1)连接AG.
∵∠DAB=∠CAE,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE.
在△ADC和△ABE中,,
∴△ADC≌△ABE(SAS),∴DC=BE,∠ADC=∠ABE.
∵G、F分别是DC与BE的中点,
∴DGDC,BFBE,∴DG=BF.
在△ADG和△ABF中,,
∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,
∴∠AGF=∠AFG,∠DAG﹣∠BAG=∠BAF﹣∠BAG,∴∠DAB=∠GAF.
∵∠DAB=60°,∴∠GAF=60°.
∵∠GAF+∠AFG+∠AGF=180°,∴∠AFG=60°;故答案为 60°,
(2)连接AG,如图2,
∵∠DAB=90°,∠DAB=∠GAF,(已证)∴∠GAF=90°,
∵AG=AF,∴∠AFG×(180°﹣90°)=45°;故答案为 45°,
(3)连接AG,如图3,
∵∠DAB=α,∠DAB=∠GAF,(已证)∴∠GAF=α,
∵AG=AF,∴∠AFG(180°﹣α).
【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADC≌△ABE和△ADG≌△ABF是解题的关键.
7.如图在△ABC和△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE交于点M.
(1)如图1,当点B,C,D在同一条直线上,且∠ACB=∠DCE=45°时,可以得到图中的一对全等三角形,即____________;(2)当点D不在直线BC上时,如图2位置,且∠ACB=∠DCE=α.
①试说明AD=BE;②直接写出∠EMD的大小(用含α的代数式表示).
【答案】(1)△BCE,△ACD(2)①见解析;②∠EMD=α.
【分析】(1)由“SAS”可证△BCE≌△ACD;(2)①由“SAS”可证△BCE≌△ACD,可得AD=BE,
②由全等三角形的性质可得∠CAD=∠CBE,由三角形的内角和定理可求解.
(1)解:∵∠ACB=∠DCE=45°,∴∠ACD=∠BCE,在△BCE和△ACD中,,∴△BCE≌△ACD(SAS),故答案为:△BCE,△ACD;
(2)①证明:∵∠ACB=∠DCE=α,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE;②解:∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠BAC+∠ABC=180°-α,∴∠BAM+∠ABM=180°-α,∴∠AMB=∠EMD=180°-(180°-α)=α.
【点睛】本题考查了全等三角形的判定和性质,证明△ACD≌△BCE是解题的关键.
8.(1)如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.某同学做了如下探究,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应该是______.
(2)如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否依然成立?若成立,请说明理由;若不成立,写出正确的结论,并说明理由.
(3)如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【答案】(1)EF=BE+DF;(2)结论EF=BE+DF仍然成立;理由见解析;(3)此时两舰艇之间的距离是210海里
【分析】(1)根据题意证明△ABE≌△ADG,△AEF≌△AGF,可得EF=FG,根据FG=DG+DF=BE+DF,可得EF=BE+DF;(2)延长FD到点G.使DG=BE.连结AG,同(1)的方法证明即可;
(3)连接EF,延长AE、BF相交于点C,应用(2)的结论可得EF=AE+BF进而气得的长,即两舰艇之间的距离
【详解】(1)EF=BE+DF,证明如下:
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△AGF中,,
∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+DF,∴EF=BE+DF;故答案为 EF=BE+DF.
(2)结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连结AG,如图②,
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,∴∠EAF=∠GAF,
在△AEF和△AGF中,
,∴△AEF≌△AGF(SAS),∴EF=FG,
∵FG=DG+DF=BE+DF,∴EF=BE+DF;
(3)如图③,连接EF,延长AE、BF相交于点C,
∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EOF=∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,∴结论EF=AE+BF成立,
即EF=1.5×(60+80)=210海里.
答:此时两舰艇之间的距离是210海里.
【点睛】本题考查全等三角形的性质与判定,方位角的计算,掌握全等三角形的性质与判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
