2024-2025学年广西柳州六中高二(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广西柳州六中高二(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 74.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 14:58:17 | ||
图片预览



文档简介
2024-2025学年广西柳州六中高二(上)开学数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.复数的虚部为( )
A. B. C. D.
2.已知集合,,则是的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 既不充分又不必要条件 D. 充要条件
3.已知个数,,的平均数为,方差为,则数,,的平均数和方差分别为( )
A. , B. , C. , D. ,
4.已知,则( )
A. B. C. D.
5.某学生参与一种答题游戏,需要从,,三道试题中选出一道进行回答,回答正确即可获得奖品.若该学生选择,,的概率分别为,,,答对,,的概率分别为,,,则其获得奖品的概率为( )
A. B. C. D.
6.已知,,且,则( )
A. B. C. D.
7.已知,,,则,,的大小关系为( )
A. B. C. D.
8.已知函数,令,则下列说法正确的是( )
A. 函数的增区间为
B. 当有个零点时,
C. 当时,的所有零点之和为
D. 当时,有个零点
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知向量,,则( )
A. 若与垂直,则 B. 若,则的值为
C. 若,则 D. 若,则与的夹角为
10.已知直线是函数图象的一条对称轴,则( )
A. B. 的图象关于点对称
C. 的图象关于直线对称 D. 在上单调递减
11.已知一个正八面体如图所示,,则( )
A. 平面
B. 点到平面的距离为
C. 异面直线与所成的角为
D. 四棱锥外接球的表面积为
三、填空题:本题共3小题,每小题5分,共15分。
12.设、均为正数,且,则的最小值为______.
13.函数的部分图象如图所示,将的图象向右平移个单位后得到函数的图象则函数的解析式为______.
14.世纪英国数学家辛卜森运用定积分,推导出了现在中学数学教材中柱、锥、球、台等几何体的统一体积公式其中,,,分别为的上底面面积、下底面面积、中截面面积和高,我们也称为“万能求积公式”例如,已知球的半径为,可得该球的体积为;已知正四棱锥的底面边长为,高为,可得该正四棱锥的体积为类似地,运用该公式求解下列问题:如图,已知球的表面积为,若用距离球心都为的两个平行平面去截球,则夹在这两个平行平面之间的几何体的体积为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
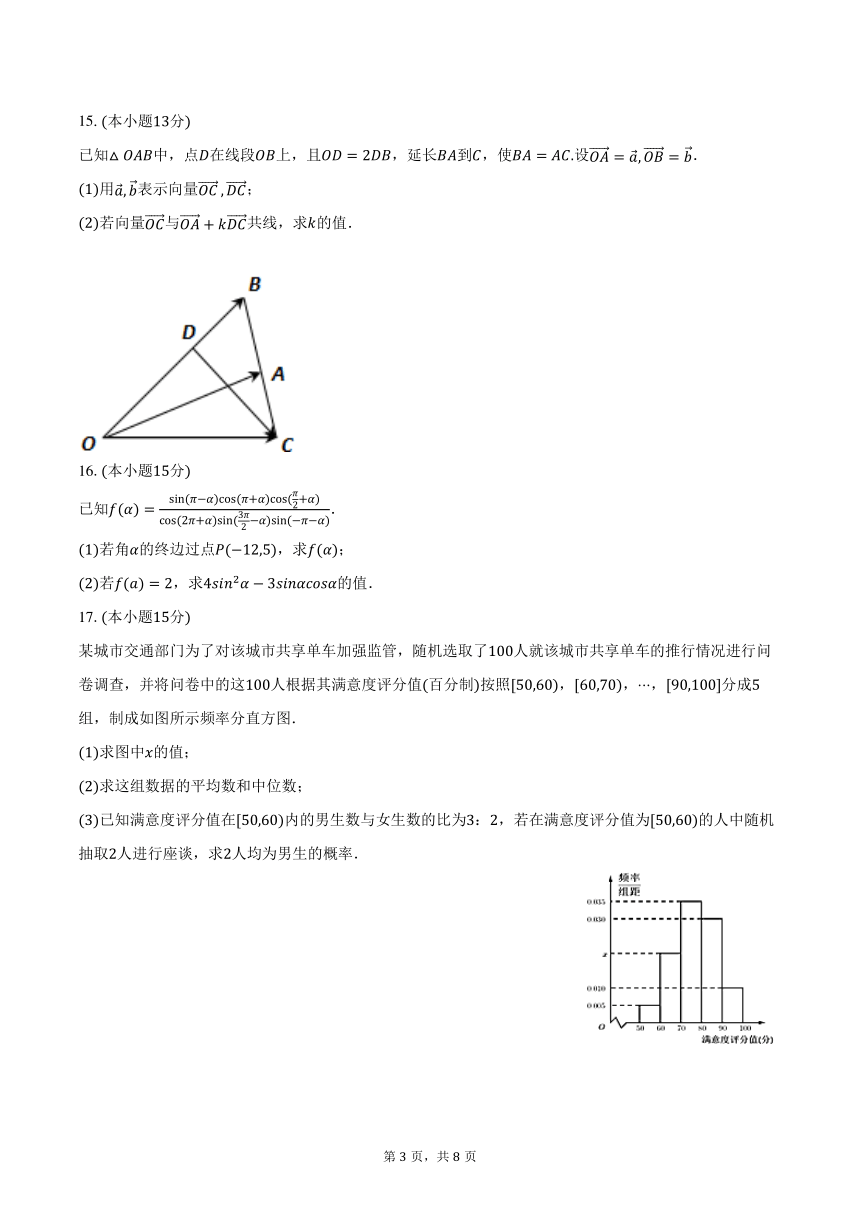
15.本小题分
已知中,点在线段上,且,延长到,使设.
用表示向量;
若向量与共线,求的值.
16.本小题分
已知.
若角的终边过点,求;
若,求的值.
17.本小题分
某城市交通部门为了对该城市共享单车加强监管,随机选取了人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这人根据其满意度评分值百分制按照,,,分成组,制成如图所示频率分直方图.
求图中的值;
求这组数据的平均数和中位数;
已知满意度评分值在内的男生数与女生数的比为:,若在满意度评分值为的人中随机抽取人进行座谈,求人均为男生的概率.
18.本小题分
已知的角,,的对边分别为,,,,,满足.
求;
若的面积为,且,点为边的中点,求的长.
19.本小题分
如图,已知等腰梯形中,,,是的中点,,将沿着翻折成,使平面平面.
求证:平面;
求与平面所成的角;
在线段上是否存在点,使得平面,若存在,求出的值;若不存在,说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:,
为的中点,
,
可得,
而.
由,得,
与共线,
设,
即,
根据平面向量基本定理,得,
解得.
16.解:
,
若角的终边过点,则,
所以.
若,则,
所以.
17.解:由,解得.
这组数据的平均数为.
中位数设为,则,解得.
满意度评分值在内有人,其中男生人,女生人.记为,,,,,
记“满意度评分值为的人中随机抽取人进行座谈,恰有名女生”为事件,
从人中抽取人有:,,,,,,,,,
所以总基本事件个数为个,包含的基本事件个数为个,
所以 .
18.解:的角,,的对边分别为,,,,,且,
所以,
可得,
由正弦定理可得,整理得到,
所以,
又,
故A;
因为,
因为,,
所以,可得,
又,
所以,,
所以的面积为,解得,
在中,由余弦定理可得.
19.证明:,是的中点,,
故四边形是菱形,从而,
沿着翻折成后,,,
又,
平面,
由题意,易知,,
四边形是平行四边形,故AE,
平面;
解:平面,
与平面所成的角为,
由已知条件,可知,,
是正三角形,,
与平面所成的角为;
假设线段上是存在点,使得平面,
过点作交于,连结,,如下图:
,,,, 四点共面,
又平面,,
四边形为平行四边形,故,
为中点,
故在线段上存在点,使得平面,且.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.复数的虚部为( )
A. B. C. D.
2.已知集合,,则是的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 既不充分又不必要条件 D. 充要条件
3.已知个数,,的平均数为,方差为,则数,,的平均数和方差分别为( )
A. , B. , C. , D. ,
4.已知,则( )
A. B. C. D.
5.某学生参与一种答题游戏,需要从,,三道试题中选出一道进行回答,回答正确即可获得奖品.若该学生选择,,的概率分别为,,,答对,,的概率分别为,,,则其获得奖品的概率为( )
A. B. C. D.
6.已知,,且,则( )
A. B. C. D.
7.已知,,,则,,的大小关系为( )
A. B. C. D.
8.已知函数,令,则下列说法正确的是( )
A. 函数的增区间为
B. 当有个零点时,
C. 当时,的所有零点之和为
D. 当时,有个零点
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知向量,,则( )
A. 若与垂直,则 B. 若,则的值为
C. 若,则 D. 若,则与的夹角为
10.已知直线是函数图象的一条对称轴,则( )
A. B. 的图象关于点对称
C. 的图象关于直线对称 D. 在上单调递减
11.已知一个正八面体如图所示,,则( )
A. 平面
B. 点到平面的距离为
C. 异面直线与所成的角为
D. 四棱锥外接球的表面积为
三、填空题:本题共3小题,每小题5分,共15分。
12.设、均为正数,且,则的最小值为______.
13.函数的部分图象如图所示,将的图象向右平移个单位后得到函数的图象则函数的解析式为______.
14.世纪英国数学家辛卜森运用定积分,推导出了现在中学数学教材中柱、锥、球、台等几何体的统一体积公式其中,,,分别为的上底面面积、下底面面积、中截面面积和高,我们也称为“万能求积公式”例如,已知球的半径为,可得该球的体积为;已知正四棱锥的底面边长为,高为,可得该正四棱锥的体积为类似地,运用该公式求解下列问题:如图,已知球的表面积为,若用距离球心都为的两个平行平面去截球,则夹在这两个平行平面之间的几何体的体积为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知中,点在线段上,且,延长到,使设.
用表示向量;
若向量与共线,求的值.
16.本小题分
已知.
若角的终边过点,求;
若,求的值.
17.本小题分
某城市交通部门为了对该城市共享单车加强监管,随机选取了人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这人根据其满意度评分值百分制按照,,,分成组,制成如图所示频率分直方图.
求图中的值;
求这组数据的平均数和中位数;
已知满意度评分值在内的男生数与女生数的比为:,若在满意度评分值为的人中随机抽取人进行座谈,求人均为男生的概率.
18.本小题分
已知的角,,的对边分别为,,,,,满足.
求;
若的面积为,且,点为边的中点,求的长.
19.本小题分
如图,已知等腰梯形中,,,是的中点,,将沿着翻折成,使平面平面.
求证:平面;
求与平面所成的角;
在线段上是否存在点,使得平面,若存在,求出的值;若不存在,说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:,
为的中点,
,
可得,
而.
由,得,
与共线,
设,
即,
根据平面向量基本定理,得,
解得.
16.解:
,
若角的终边过点,则,
所以.
若,则,
所以.
17.解:由,解得.
这组数据的平均数为.
中位数设为,则,解得.
满意度评分值在内有人,其中男生人,女生人.记为,,,,,
记“满意度评分值为的人中随机抽取人进行座谈,恰有名女生”为事件,
从人中抽取人有:,,,,,,,,,
所以总基本事件个数为个,包含的基本事件个数为个,
所以 .
18.解:的角,,的对边分别为,,,,,且,
所以,
可得,
由正弦定理可得,整理得到,
所以,
又,
故A;
因为,
因为,,
所以,可得,
又,
所以,,
所以的面积为,解得,
在中,由余弦定理可得.
19.证明:,是的中点,,
故四边形是菱形,从而,
沿着翻折成后,,,
又,
平面,
由题意,易知,,
四边形是平行四边形,故AE,
平面;
解:平面,
与平面所成的角为,
由已知条件,可知,,
是正三角形,,
与平面所成的角为;
假设线段上是存在点,使得平面,
过点作交于,连结,,如下图:
,,,, 四点共面,
又平面,,
四边形为平行四边形,故,
为中点,
故在线段上存在点,使得平面,且.
第1页,共1页
同课章节目录
