北京交通大学附属中学2025届九年级上册开学练习数学试题(PDF版,无答案)
文档属性
| 名称 | 北京交通大学附属中学2025届九年级上册开学练习数学试题(PDF版,无答案) | 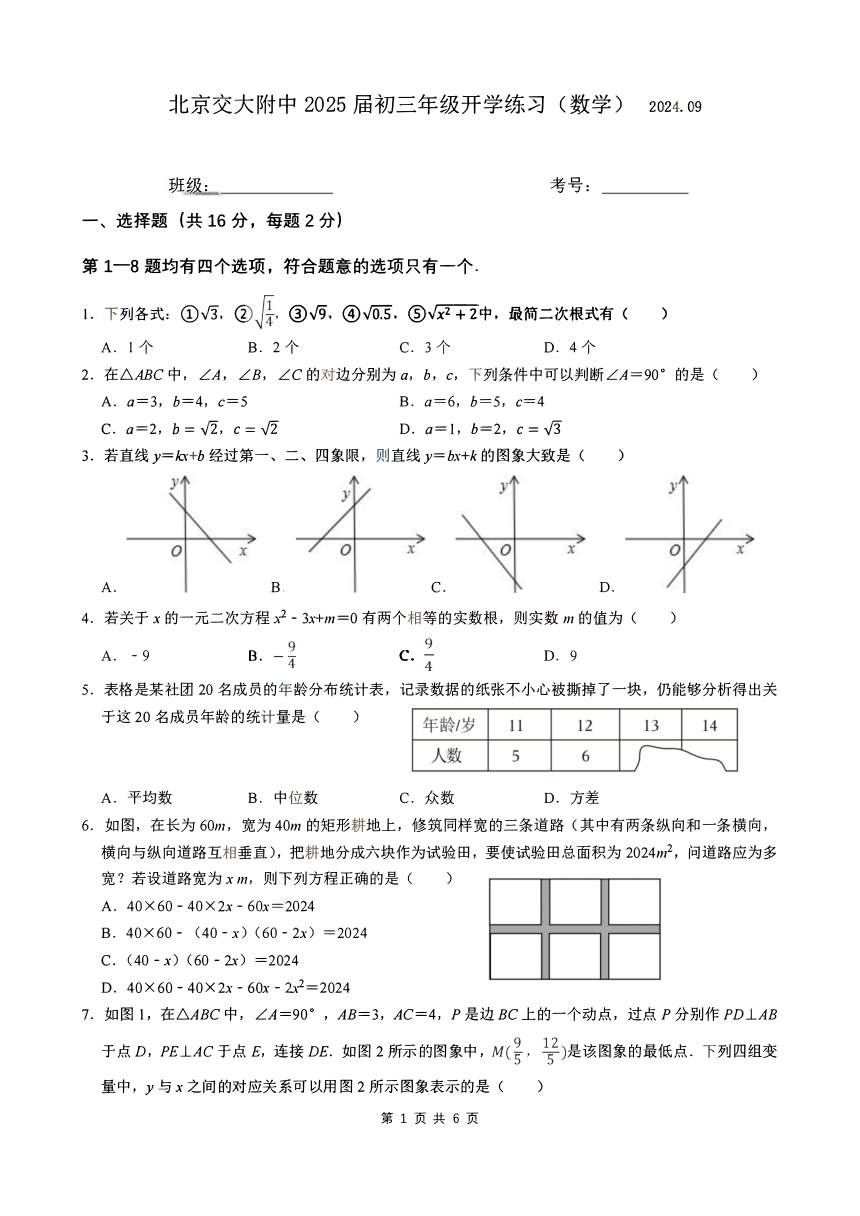 | |
| 格式 | |||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 16:51:07 | ||
图片预览



文档简介
北京交大附中2025届初三年级开学练习 (数学) 2024.09
班级: 考号:
一、 选择题 (共 16分,每题2分)
第1—8题均有四个选项, 符合题意的选项只有一个.
1. 下列各式 : ① √3,Q ③√5,④√05,⑤VF+2中, 最简二次根式有 ( )
A. 1个 B. 2个 C.3个 D. 4个
2. 在△ABC中, ∠A,∠B, ∠C的对边分别为 a, b,c,下列条件中可以判断∠A=90° 的是 ( )
A. a=3, b=4, c=5 B.a=6, b=5,c=4
C. a=2, b=√2, c=√Z D.a=1,b=2, c=V3
3.若直线y=kx+b经过第一、 二、四象限, 则直线y=bx+k的 图象大致是 ( )
A. B . C. D.
4.若关于x的一元二次方程x -3x+m=0有两个相等的实数根,则实数m的值为 ( )
A. -9 8. c D. 9
5. 表格是某社团20名成员的年龄分布统计表,记录数据的纸张不小心被撕掉了一块,仍能够分析得出关
于这20名成员年龄的统计量是 ( )
A.平均数 B. 中位数 C. 众数 D.方差
6.如图,在长为60m, 宽为40m的矩形耕地上,修筑同样宽的三条道路 (其中有两条纵向和一条横向,
横向与纵向道路互相垂直),把耕地分成六块作为试验田,要使试验田总面积为2024m , 问道路应为多
宽 若设道路宽为xm, 则下列方程正确的是 ( )
A. 40×60-40×2x-60x=2024
B. 40×60- (40-x) (60-2x) =2024
C.(40-x) (60-2x) = 2024
D. 40×60-40×2x-60x-2x =2024
7. 如图 1,在△ABC中,∠A=90° ,AB=3, AC=4, P是边BC上的一个动点,过点P分别作PD⊥AB
于点D, PE⊥AC于点E, 连接DE. 如图2所示的图象中, 是该图象的最低点. 下列四组变
量中, y与 x之间的对应关系可以用图2所示图象表示的是 ( )
第 1 页 共 6 页
A.点 P与 B的距离为 x,点 P与 C的距离为 y B.点 P与 D的距离为 x,点 D与 E的距离为 y
C.点 P与 D的距离为 x,点 P与 E的距离为 y D.点 P与 B的距离为 x,点 D与 E的距离为 y
8.如图,点 A,B,C在同一条直线上,点 B在点 A,C之间,点 D,E在直线 AC同侧,AB<BC,∠A
=∠C=90°,△EAB≌△BCD,连接 DE.设 AB=a,BC=b,DE=c,给出下面三个结论:
①a+b<c; ②a+b> 2 + 2; ③ 2(a+b)>c.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(共 16 分,每题 2 分)
9.式子 2 4在实数范围内有意义,则 x的取值范围是 .
10.将直线 y=kx+3向上平移 3个单位长度后经过点(1,4),则 k的值是 .
11.在 ABCD中,若∠A=∠B+50°,则∠B的度数为 度.
12.已知 x=2是一元二次方程 x2﹣2mx+4=0的一个解,则 m的值为 .
13.将抛物线 y=2x2 向上平移 2 个单位长度,再向右平移 3 个单位长度后,得到的抛物线的表达式
为 .
14.在一次演讲比赛中,甲的演讲内容 90分、演讲能力 80分、演讲效果 90分,若按照演讲内容占 50%,
演讲能力占 40%,演讲效果占 10%,计算选手的综合成绩,则该选手的综合成绩为 .
15.如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,∠AOB= 60°,AB=2,那么 BC 的长
是 .
16.已知抛物线 y=ax2+bx+c(a,b,c是常数,a≠0)经过点(﹣1,﹣1)和(0,1),当 x=﹣2时,与
其对应的函数值 y>1.有下列结论:①abc>0;②关于 x的方程 ax2+bx+c+1=0有两个不等的实数根;
③a>2;④若方程 ax2+bx+c=0的两根为 x1,x2,则 x1+x2<﹣2.其中正确的有 .
三、解答题(共 68分,第 17、18题每题 4分,第 19-21题每题 6分,第 22题 5分,第 23
题 6分,第 24题 5分,第 25、26题每题 6分,第 27-28题每题 7分)解答应写出文字说明、
演算步骤或证明过程.
17.计算:(2024 )0 + ( 1 ) 13 + | 3 2| 27.
第 2 页 共 6 页
18.解方程:x2﹣2x﹣3=0.
19.在数学课上,老师布置任务:利用尺规“作以线段 AB为对角线的正方形”.
小丽的作法如下:
1
①分别以点 A、B为圆心,以大于 AB为半径作弧,两弧交于 E、F两点;
2
②连接 EF,与 AB交于点 O;
③以点 O为圆心,OA长为半径作弧,与直线 EF交于 C、D两点;
④分别连接线段 AC,BC,BD,DA.所以四边形 ADBC就是所求作的正方形.
根据小丽的作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵OA=OB,OC=OD,
∴四边形 ADBC为平行四边形.( ① )(填推理的依据)
∵OA=OB=OC=OD,即 AB=CD,
∴四边形 ADBC为矩形.( ② )(填推理的依据)
∵CD ③ AB,
∴四边形 ADBC为正方形.
20.已知关于 x的一元二次方程 x2﹣(m+3)x+2+m=0.
(1)求证:对于任意实数 m,该方程总有实数根;
(2)若这个一元二次方程的一根大于 2,求 m的取值范围.
21.已知二次函数 y=ax2+bx+c自变量 x与函数 y的部分对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 4 …
y … 5 0 ﹣3 ﹣4 ﹣3 0 m …
(1)二次函数图象的开口方向 ,顶点坐标是 ,m的值为 ;
(2)点 P(﹣3,y1)、Q(2,y2)在函数图象上,y1 y2(填<、>、=);
(3)当 y<0时,x的取值范围是 ;
(4)关于 x的一元二次方程 ax2+bx+c=5的解为 .
第 3 页 共 6 页
22.在平面直角坐标系 xOy中,函数 y=kx+b(k≠0)与 y=﹣kx+3的图象交于点(2,1).
(1)求 k,b的值;
(2)当 x>2时,对于 x的每一个值,函数 y=mx(m≠0)的值既大于函数 y=kx+b的值,也大于函数
y=﹣kx+3的值,直接写出 m的取值范围.
23.如图,在△ABC中,∠CAB=90°,点 D,E分别是 BC,AC的中点.连接 DE并延长至点 F,使得
EF=DE.连接 AF,CF,AD.
(1)求证:四边形 ADCF是菱形;
(2)连接 BF,若∠ACB=60°,AF=2,求 BF的长.
24.某学校举办的“青春飞扬”主题演讲比赛分为初赛和决赛两个阶段.
(1)初赛由 10名教师评委和 45名学生评委给每位选手打分(百分制).对评委给某位选手的打分进行
整理、描述和分析.下面给出了部分信息.
a.教师评委打分:
86 88 90 91 91 91 91 92 92 98
b.学生评委打分的频数分布直方图如图(数据分 6组:第 1组 82≤x<85,第 2组 85≤x<88,第 3组
88≤x<91,第 4组 91≤x<94,第 5组 94≤x<97,第 6组 97≤x≤100):
c.评委打分的平均数、中位数、众数如下:
平均数 中位数 众数
教师评委 91 91 m
学生评委 90.8 n 93
根据以上信息,回答下列问题:
①m的值为 ,n的值位于学生评委打分数据分组的第 组;
②若去掉教师评委打分中的最高分和最低分,记其余 8 名教师评委打分的平均数为 ,则 91
(填“>”“=”或“<”);
第 4 页 共 6 页
(2)决赛由 5名专业评委给每位选手打分(百分制).对每位选手,计算 5名专业评委给其打分的平均
数和方差.平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前.5名专业评委给进
入决赛的甲、乙、丙三位选手的打分如下:
评委 1 评委 2 评委 3 评委 4 评委 5
甲 93 90 92 93 92
乙 91 92 92 92 92
丙 90 94 90 94 k
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前的是 ,表中 k(k为整数)
的值为 .
25.电缆在空中架设时,两端挂起的电缆下垂可以近似的看成抛物线的形状.如图,在一个斜坡 BD上按
水平距离间隔 60米架设两个塔柱,每个塔柱固定电缆的位置离地面高度为 27米(AB=CD=27米),
以过点 A的水平线为 x轴,水平线与电缆的另一个交点为原点 O建立平面直角坐标系,如图所示.经
测量,AO=40米,斜坡高度 12米(即 B、D两点的铅直高度差).
结合上面信息,回答问题:
(1)若以 1 米为一个单位长度,则 D 点坐标为 ,下垂电缆的抛物线表达式
为 ;
(2)若电缆下垂的安全高度是 13.5米,即电缆距离坡面铅直高度的最小值不小于 13.5米时,符合安全
要求,否则存在安全隐患.(说明:直线 GH⊥x轴分别交直线 BD和抛物线于点 H、G.点 G距离坡面
的铅直高度为 GH的长),请判断上述这种电缆的架设是否符合安全要求?请说明理由.
26.在平面直角坐标系 xOy中,点(x1,m),(x2,n)在抛物线 y=ax2+bx+c(a>0)上,设抛物线的对
称轴为直线 x=t.
(1)若对于 x1=1,x2=3,有 m=n,求 t的值;
(2)若对于 t﹣1<x1<t,2<x2<3,存在 m>n,求 t的取值范围.
第 5 页 共 6 页
27.已知:在正方形 ABCD中,点 E是 BC延长线上一点,且 CE≠BC,连接 DE,过点 D作 DE的垂线
交直线 AB于点 F,连接 EF,取 EF的中点 G,连接 CG.
(1)当 CE<BC时,
①补全图 1;
②求证:△ADF≌△CDE;
③用等式表示线段 CD,CE,CG之间的数量关系,并证明;
(2)如图 2,当 CE>BC时,请你直接写出线段 CD,CE,CG之间的数量关系.
28. 在平面直角坐标系 xOy中,M为平面内一点.对于点 P和图形 W给出如下定义:若图形 W上存在点
Q,使得点 P与点 Q关于点 M对称,则称点 P为图形 W关于点 M的“中心镜像对称点”.
(1)如图 1,A(﹣1,1),B(2,1).
1
①在点 P1(﹣2,﹣1),P2(0,﹣2),P3( ,﹣1),P4(2,﹣1)中,线段 AB关于点 M(0,0)的2
“中心镜像对称点”是 ;
②若点 P(1,﹣3)是线段 AB关于点 M(m,n)的“中心镜像对称点”,请直接写出点 M的横坐标 m
的取值范围;
(2)如图 2,矩形 CDEF中,C(2,﹣1),D(﹣2,﹣1),E(﹣2,1),F(2,1).若直线 y=x+m
上存在矩形 CDEF关于点 M(m,2)的“中心镜像对称点”,请直接写出 m的取值范围.
第 6 页 共 6 页
班级: 考号:
一、 选择题 (共 16分,每题2分)
第1—8题均有四个选项, 符合题意的选项只有一个.
1. 下列各式 : ① √3,Q ③√5,④√05,⑤VF+2中, 最简二次根式有 ( )
A. 1个 B. 2个 C.3个 D. 4个
2. 在△ABC中, ∠A,∠B, ∠C的对边分别为 a, b,c,下列条件中可以判断∠A=90° 的是 ( )
A. a=3, b=4, c=5 B.a=6, b=5,c=4
C. a=2, b=√2, c=√Z D.a=1,b=2, c=V3
3.若直线y=kx+b经过第一、 二、四象限, 则直线y=bx+k的 图象大致是 ( )
A. B . C. D.
4.若关于x的一元二次方程x -3x+m=0有两个相等的实数根,则实数m的值为 ( )
A. -9 8. c D. 9
5. 表格是某社团20名成员的年龄分布统计表,记录数据的纸张不小心被撕掉了一块,仍能够分析得出关
于这20名成员年龄的统计量是 ( )
A.平均数 B. 中位数 C. 众数 D.方差
6.如图,在长为60m, 宽为40m的矩形耕地上,修筑同样宽的三条道路 (其中有两条纵向和一条横向,
横向与纵向道路互相垂直),把耕地分成六块作为试验田,要使试验田总面积为2024m , 问道路应为多
宽 若设道路宽为xm, 则下列方程正确的是 ( )
A. 40×60-40×2x-60x=2024
B. 40×60- (40-x) (60-2x) =2024
C.(40-x) (60-2x) = 2024
D. 40×60-40×2x-60x-2x =2024
7. 如图 1,在△ABC中,∠A=90° ,AB=3, AC=4, P是边BC上的一个动点,过点P分别作PD⊥AB
于点D, PE⊥AC于点E, 连接DE. 如图2所示的图象中, 是该图象的最低点. 下列四组变
量中, y与 x之间的对应关系可以用图2所示图象表示的是 ( )
第 1 页 共 6 页
A.点 P与 B的距离为 x,点 P与 C的距离为 y B.点 P与 D的距离为 x,点 D与 E的距离为 y
C.点 P与 D的距离为 x,点 P与 E的距离为 y D.点 P与 B的距离为 x,点 D与 E的距离为 y
8.如图,点 A,B,C在同一条直线上,点 B在点 A,C之间,点 D,E在直线 AC同侧,AB<BC,∠A
=∠C=90°,△EAB≌△BCD,连接 DE.设 AB=a,BC=b,DE=c,给出下面三个结论:
①a+b<c; ②a+b> 2 + 2; ③ 2(a+b)>c.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(共 16 分,每题 2 分)
9.式子 2 4在实数范围内有意义,则 x的取值范围是 .
10.将直线 y=kx+3向上平移 3个单位长度后经过点(1,4),则 k的值是 .
11.在 ABCD中,若∠A=∠B+50°,则∠B的度数为 度.
12.已知 x=2是一元二次方程 x2﹣2mx+4=0的一个解,则 m的值为 .
13.将抛物线 y=2x2 向上平移 2 个单位长度,再向右平移 3 个单位长度后,得到的抛物线的表达式
为 .
14.在一次演讲比赛中,甲的演讲内容 90分、演讲能力 80分、演讲效果 90分,若按照演讲内容占 50%,
演讲能力占 40%,演讲效果占 10%,计算选手的综合成绩,则该选手的综合成绩为 .
15.如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,∠AOB= 60°,AB=2,那么 BC 的长
是 .
16.已知抛物线 y=ax2+bx+c(a,b,c是常数,a≠0)经过点(﹣1,﹣1)和(0,1),当 x=﹣2时,与
其对应的函数值 y>1.有下列结论:①abc>0;②关于 x的方程 ax2+bx+c+1=0有两个不等的实数根;
③a>2;④若方程 ax2+bx+c=0的两根为 x1,x2,则 x1+x2<﹣2.其中正确的有 .
三、解答题(共 68分,第 17、18题每题 4分,第 19-21题每题 6分,第 22题 5分,第 23
题 6分,第 24题 5分,第 25、26题每题 6分,第 27-28题每题 7分)解答应写出文字说明、
演算步骤或证明过程.
17.计算:(2024 )0 + ( 1 ) 13 + | 3 2| 27.
第 2 页 共 6 页
18.解方程:x2﹣2x﹣3=0.
19.在数学课上,老师布置任务:利用尺规“作以线段 AB为对角线的正方形”.
小丽的作法如下:
1
①分别以点 A、B为圆心,以大于 AB为半径作弧,两弧交于 E、F两点;
2
②连接 EF,与 AB交于点 O;
③以点 O为圆心,OA长为半径作弧,与直线 EF交于 C、D两点;
④分别连接线段 AC,BC,BD,DA.所以四边形 ADBC就是所求作的正方形.
根据小丽的作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵OA=OB,OC=OD,
∴四边形 ADBC为平行四边形.( ① )(填推理的依据)
∵OA=OB=OC=OD,即 AB=CD,
∴四边形 ADBC为矩形.( ② )(填推理的依据)
∵CD ③ AB,
∴四边形 ADBC为正方形.
20.已知关于 x的一元二次方程 x2﹣(m+3)x+2+m=0.
(1)求证:对于任意实数 m,该方程总有实数根;
(2)若这个一元二次方程的一根大于 2,求 m的取值范围.
21.已知二次函数 y=ax2+bx+c自变量 x与函数 y的部分对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 4 …
y … 5 0 ﹣3 ﹣4 ﹣3 0 m …
(1)二次函数图象的开口方向 ,顶点坐标是 ,m的值为 ;
(2)点 P(﹣3,y1)、Q(2,y2)在函数图象上,y1 y2(填<、>、=);
(3)当 y<0时,x的取值范围是 ;
(4)关于 x的一元二次方程 ax2+bx+c=5的解为 .
第 3 页 共 6 页
22.在平面直角坐标系 xOy中,函数 y=kx+b(k≠0)与 y=﹣kx+3的图象交于点(2,1).
(1)求 k,b的值;
(2)当 x>2时,对于 x的每一个值,函数 y=mx(m≠0)的值既大于函数 y=kx+b的值,也大于函数
y=﹣kx+3的值,直接写出 m的取值范围.
23.如图,在△ABC中,∠CAB=90°,点 D,E分别是 BC,AC的中点.连接 DE并延长至点 F,使得
EF=DE.连接 AF,CF,AD.
(1)求证:四边形 ADCF是菱形;
(2)连接 BF,若∠ACB=60°,AF=2,求 BF的长.
24.某学校举办的“青春飞扬”主题演讲比赛分为初赛和决赛两个阶段.
(1)初赛由 10名教师评委和 45名学生评委给每位选手打分(百分制).对评委给某位选手的打分进行
整理、描述和分析.下面给出了部分信息.
a.教师评委打分:
86 88 90 91 91 91 91 92 92 98
b.学生评委打分的频数分布直方图如图(数据分 6组:第 1组 82≤x<85,第 2组 85≤x<88,第 3组
88≤x<91,第 4组 91≤x<94,第 5组 94≤x<97,第 6组 97≤x≤100):
c.评委打分的平均数、中位数、众数如下:
平均数 中位数 众数
教师评委 91 91 m
学生评委 90.8 n 93
根据以上信息,回答下列问题:
①m的值为 ,n的值位于学生评委打分数据分组的第 组;
②若去掉教师评委打分中的最高分和最低分,记其余 8 名教师评委打分的平均数为 ,则 91
(填“>”“=”或“<”);
第 4 页 共 6 页
(2)决赛由 5名专业评委给每位选手打分(百分制).对每位选手,计算 5名专业评委给其打分的平均
数和方差.平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前.5名专业评委给进
入决赛的甲、乙、丙三位选手的打分如下:
评委 1 评委 2 评委 3 评委 4 评委 5
甲 93 90 92 93 92
乙 91 92 92 92 92
丙 90 94 90 94 k
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前的是 ,表中 k(k为整数)
的值为 .
25.电缆在空中架设时,两端挂起的电缆下垂可以近似的看成抛物线的形状.如图,在一个斜坡 BD上按
水平距离间隔 60米架设两个塔柱,每个塔柱固定电缆的位置离地面高度为 27米(AB=CD=27米),
以过点 A的水平线为 x轴,水平线与电缆的另一个交点为原点 O建立平面直角坐标系,如图所示.经
测量,AO=40米,斜坡高度 12米(即 B、D两点的铅直高度差).
结合上面信息,回答问题:
(1)若以 1 米为一个单位长度,则 D 点坐标为 ,下垂电缆的抛物线表达式
为 ;
(2)若电缆下垂的安全高度是 13.5米,即电缆距离坡面铅直高度的最小值不小于 13.5米时,符合安全
要求,否则存在安全隐患.(说明:直线 GH⊥x轴分别交直线 BD和抛物线于点 H、G.点 G距离坡面
的铅直高度为 GH的长),请判断上述这种电缆的架设是否符合安全要求?请说明理由.
26.在平面直角坐标系 xOy中,点(x1,m),(x2,n)在抛物线 y=ax2+bx+c(a>0)上,设抛物线的对
称轴为直线 x=t.
(1)若对于 x1=1,x2=3,有 m=n,求 t的值;
(2)若对于 t﹣1<x1<t,2<x2<3,存在 m>n,求 t的取值范围.
第 5 页 共 6 页
27.已知:在正方形 ABCD中,点 E是 BC延长线上一点,且 CE≠BC,连接 DE,过点 D作 DE的垂线
交直线 AB于点 F,连接 EF,取 EF的中点 G,连接 CG.
(1)当 CE<BC时,
①补全图 1;
②求证:△ADF≌△CDE;
③用等式表示线段 CD,CE,CG之间的数量关系,并证明;
(2)如图 2,当 CE>BC时,请你直接写出线段 CD,CE,CG之间的数量关系.
28. 在平面直角坐标系 xOy中,M为平面内一点.对于点 P和图形 W给出如下定义:若图形 W上存在点
Q,使得点 P与点 Q关于点 M对称,则称点 P为图形 W关于点 M的“中心镜像对称点”.
(1)如图 1,A(﹣1,1),B(2,1).
1
①在点 P1(﹣2,﹣1),P2(0,﹣2),P3( ,﹣1),P4(2,﹣1)中,线段 AB关于点 M(0,0)的2
“中心镜像对称点”是 ;
②若点 P(1,﹣3)是线段 AB关于点 M(m,n)的“中心镜像对称点”,请直接写出点 M的横坐标 m
的取值范围;
(2)如图 2,矩形 CDEF中,C(2,﹣1),D(﹣2,﹣1),E(﹣2,1),F(2,1).若直线 y=x+m
上存在矩形 CDEF关于点 M(m,2)的“中心镜像对称点”,请直接写出 m的取值范围.
第 6 页 共 6 页
同课章节目录
