2024-2025学年福建省福州一中九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年福建省福州一中九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 20:59:05 | ||
图片预览




文档简介
2024-2025学年福建省福州一中九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.在平面直角坐标系中,点关于轴对称的点的坐标为( )
A. B. C. D.
3.如图,在中,,,若,则( )
A. B.
C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.下列长度的三条线段能组成三角形的是( )
A. ,, B. ,, C. ,, D. ,,
6.某校举行“英语单词拼写比赛”,个班级代表队的正确答题数如图这个正确答题数所组成的一组数据的众数和中位数是( )
A. ,
B. ,
C. ,
D. ,
7.如图,直线和直线相交于点,若,则的度数是( )
A. B.
C. D.
8.某校七年级组织一次篮球赛,各班均组队参赛,赛制为每两班之间赛两场,共需安排场比赛设七年级共有个班,则下列方程正确的是( )
A. B. C. D.
9.如图,菱形中,对角线、相交于点,为边中点,,菱形的面积为,则
的长等于( )
A. B. C. D.
10.已知二次函数的图象与轴交于不同两点,与轴的交点在轴正半轴,它的对称轴为直线,有以下结论:,,抛物线上有两点和,若,且,则,设,是方程的两根,若,则,其中正确的结论是( )
A. B. C. D.
二、填空题:本题共7小题,共27分。
11.据报道,受台风“摩羯”影响,海口全市受灾人口万人,造成直接经济损失约亿元,数据亿元用科学记数法表示为______元
12.如果与是同类项,那么 ______.
13.因式分解: .
14.如图,已知,于点点对应的数是,点对应的数是,,那么数轴上点所表示的数是______.
15.当时,整式的值为,则当时,整式的值为______.
16.如图,正方形中边长为,为上一点,且,为边上的一个动点,连接,以为边向右侧作等边,连接,则的最小值为______.
17.如图,菱形中的对角线,相交于点,,.
求证:四边形是矩形.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
计算:;
解方程:.
19.本小题分
如图,,,求证:≌.
20.本小题分
先化简、再求值,其中.
21.本小题分
为了了解某校中学生音乐期末成绩分布情况,随机调查了部分参加期末测试的学生的音乐成绩,整理并制作了统计图表的一部分.
分数段 频数 频率
请根据图表中提供的信息,解答下列问题:
______; ______;
请用样本数据,估计该校音乐期末测试成绩的平均分;
若该校有名学生参加音乐期末测试,成绩达到分为优秀,则估计该校音乐期末测试成绩为优秀的学生人数为______.
22.本小题分
某工艺品专卖店计划购买中国结和油纸伞若干,已知购买个中国结和把油纸伞共需元,购买个中国结和把油纸伞共需元.
每个中国结和每把油纸伞的进价分别是多少元;
若该专卖店准备购买中国结和油纸伞共件,且购买中国结的数量至少比油纸伞的数量多件,请问怎样购买,才能使总费用最少,并求出最少总费用.
23.本小题分
阅读材料:如图,已知中,,请用尺规作图在边上求作点,使得小明提出想法:如图,假设点为所求作的点,连接,此时有,因为,所以,从而得到:.
由此想法得到如下作图方法:如图,以点为圆心,为半径画弧,该弧与相交于点,则点即为所作的点.
根据以上材料,完成下面两个问题:
请你类比上述作图方法,在图中,用尺规作图在边上作点,使得;
按以上要求作出,两点,当直角边长度发生变化时,求证:.
24.本小题分
如图,已知二次函数的图象与轴交于,两点点坐标为,与轴交于点,点为抛物线顶点,点为中点.
求二次函数的表达式;
在直线上方的抛物线上存在点,使得,求点的坐标;
已知,为抛物线上不与,重合的相异两点,若直线,交于点,则无论,在抛物线上如何运动,当,,三点共线时,试判断的面积是否为定值,若是,请求出定值:若不是,请说明理由.
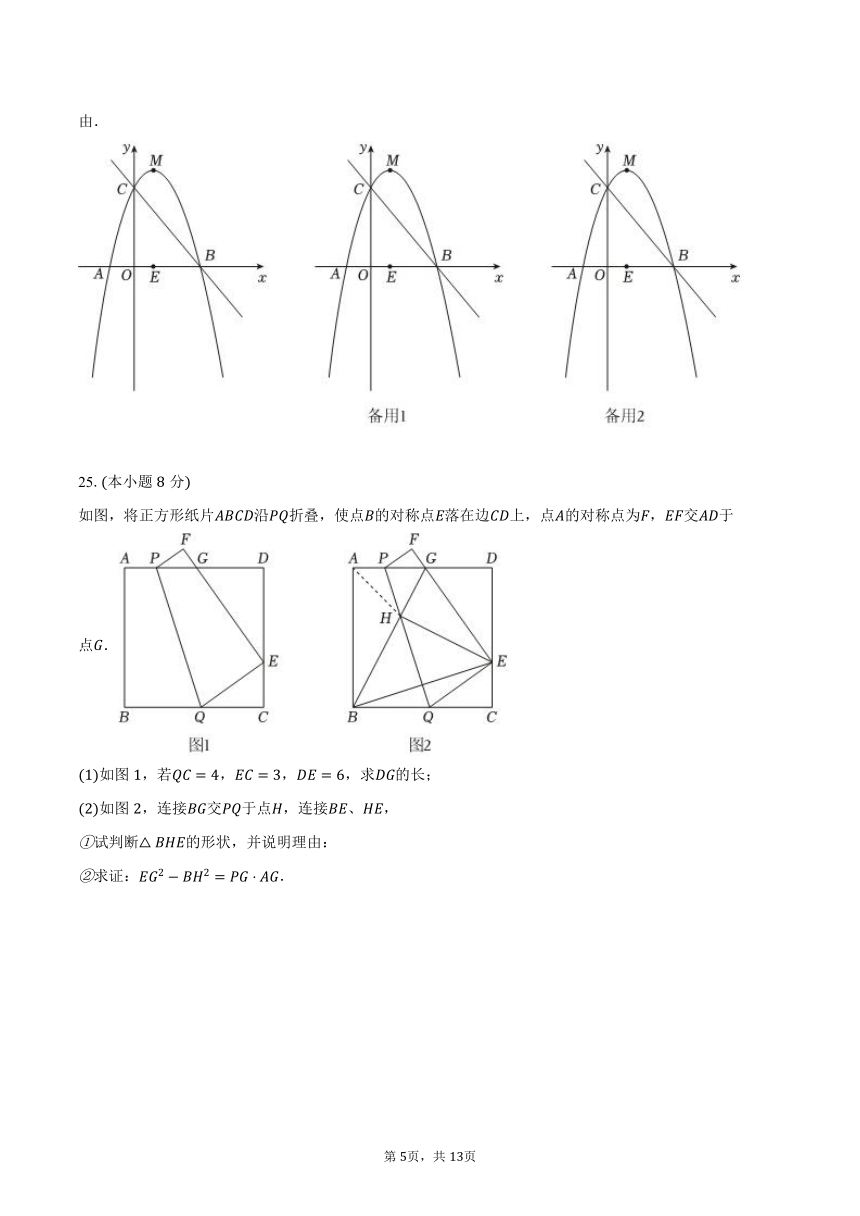
25.本小题分
如图,将正方形纸片沿折叠,使点的对称点落在边上,点的对称点为,交于点.
如图,若,,,求的长;
如图,连接交于点,连接、,
试判断的形状,并说明理由:
求证:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.证明:菱形的对角线与相交于点,
,
,,
,
四边形是矩形;
18.解:原式
;
,
,
,
,.
19.证明:在和中,
,
≌.
20.解:
,
,
原式.
21.,
22.解:设每个中国结的进价为元,每把油纸伞的进价为元,
由题意,得
解得
答:每个中国结的进价为元,每把油纸伞的进价为元.
设购买个中国结,则购买把油纸伞,
根据题意,得,
解得.
设总费用为元,则.
,
随的增大而增大.
为整数,,
当时,取得最小值,
此时,
此时.
答:购买中国结个、油纸伞把时,总费用最少,最少总费用是元.
23.解:如图,点即为所求,
;
证明:如图,
;
由作图知:,,
,,
,,
,,
,,
,
,
,
.
24.解:将,代入,
得,
解得:,
抛物线解析式为;
对于,令,则
解得:,
,
,
是等腰直角三角形,
,
,
,
如图所示,过点作交抛物线于点,过点作轴于点,
,
是等腰直角三角形,
,
设,则,
,,
,
解得:舍去或,
;
的面积为定值.
理由:
如图:
设,,
点为中点,,
,
,,三点共线,
可设直线的解析式,
代入得,
直线的解析式,
联立,
得,
,,
,,
同理直线解析式为,直线解析式为,
联立,
解得:,
,
直线解析式,直线解析式为,
,,
,,
,,
,
,
,
,
,
的面积为.
25.解:将正方形纸片沿折叠,使点的对称点落在边上,
,,,
,
∽,
,即,
;
解:是等腰直角三角形,
理由:过作,
翻折,
,,
,
,
,
又,,
≌,
,,
又,
≌,
,
,
,
,
,
是等腰直角三角形;
证明:连接,,,如图,
≌,≌,
,,
,
由折叠可得:,平分,
,,
,,
,
,
,
,
,,,四点共圆,
.
在和中,
,
≌.
,
,
,
,
,
∽,
.
.
.
第1页,共1页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.在平面直角坐标系中,点关于轴对称的点的坐标为( )
A. B. C. D.
3.如图,在中,,,若,则( )
A. B.
C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.下列长度的三条线段能组成三角形的是( )
A. ,, B. ,, C. ,, D. ,,
6.某校举行“英语单词拼写比赛”,个班级代表队的正确答题数如图这个正确答题数所组成的一组数据的众数和中位数是( )
A. ,
B. ,
C. ,
D. ,
7.如图,直线和直线相交于点,若,则的度数是( )
A. B.
C. D.
8.某校七年级组织一次篮球赛,各班均组队参赛,赛制为每两班之间赛两场,共需安排场比赛设七年级共有个班,则下列方程正确的是( )
A. B. C. D.
9.如图,菱形中,对角线、相交于点,为边中点,,菱形的面积为,则
的长等于( )
A. B. C. D.
10.已知二次函数的图象与轴交于不同两点,与轴的交点在轴正半轴,它的对称轴为直线,有以下结论:,,抛物线上有两点和,若,且,则,设,是方程的两根,若,则,其中正确的结论是( )
A. B. C. D.
二、填空题:本题共7小题,共27分。
11.据报道,受台风“摩羯”影响,海口全市受灾人口万人,造成直接经济损失约亿元,数据亿元用科学记数法表示为______元
12.如果与是同类项,那么 ______.
13.因式分解: .
14.如图,已知,于点点对应的数是,点对应的数是,,那么数轴上点所表示的数是______.
15.当时,整式的值为,则当时,整式的值为______.
16.如图,正方形中边长为,为上一点,且,为边上的一个动点,连接,以为边向右侧作等边,连接,则的最小值为______.
17.如图,菱形中的对角线,相交于点,,.
求证:四边形是矩形.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
计算:;
解方程:.
19.本小题分
如图,,,求证:≌.
20.本小题分
先化简、再求值,其中.
21.本小题分
为了了解某校中学生音乐期末成绩分布情况,随机调查了部分参加期末测试的学生的音乐成绩,整理并制作了统计图表的一部分.
分数段 频数 频率
请根据图表中提供的信息,解答下列问题:
______; ______;
请用样本数据,估计该校音乐期末测试成绩的平均分;
若该校有名学生参加音乐期末测试,成绩达到分为优秀,则估计该校音乐期末测试成绩为优秀的学生人数为______.
22.本小题分
某工艺品专卖店计划购买中国结和油纸伞若干,已知购买个中国结和把油纸伞共需元,购买个中国结和把油纸伞共需元.
每个中国结和每把油纸伞的进价分别是多少元;
若该专卖店准备购买中国结和油纸伞共件,且购买中国结的数量至少比油纸伞的数量多件,请问怎样购买,才能使总费用最少,并求出最少总费用.
23.本小题分
阅读材料:如图,已知中,,请用尺规作图在边上求作点,使得小明提出想法:如图,假设点为所求作的点,连接,此时有,因为,所以,从而得到:.
由此想法得到如下作图方法:如图,以点为圆心,为半径画弧,该弧与相交于点,则点即为所作的点.
根据以上材料,完成下面两个问题:
请你类比上述作图方法,在图中,用尺规作图在边上作点,使得;
按以上要求作出,两点,当直角边长度发生变化时,求证:.
24.本小题分
如图,已知二次函数的图象与轴交于,两点点坐标为,与轴交于点,点为抛物线顶点,点为中点.
求二次函数的表达式;
在直线上方的抛物线上存在点,使得,求点的坐标;
已知,为抛物线上不与,重合的相异两点,若直线,交于点,则无论,在抛物线上如何运动,当,,三点共线时,试判断的面积是否为定值,若是,请求出定值:若不是,请说明理由.
25.本小题分
如图,将正方形纸片沿折叠,使点的对称点落在边上,点的对称点为,交于点.
如图,若,,,求的长;
如图,连接交于点,连接、,
试判断的形状,并说明理由:
求证:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.证明:菱形的对角线与相交于点,
,
,,
,
四边形是矩形;
18.解:原式
;
,
,
,
,.
19.证明:在和中,
,
≌.
20.解:
,
,
原式.
21.,
22.解:设每个中国结的进价为元,每把油纸伞的进价为元,
由题意,得
解得
答:每个中国结的进价为元,每把油纸伞的进价为元.
设购买个中国结,则购买把油纸伞,
根据题意,得,
解得.
设总费用为元,则.
,
随的增大而增大.
为整数,,
当时,取得最小值,
此时,
此时.
答:购买中国结个、油纸伞把时,总费用最少,最少总费用是元.
23.解:如图,点即为所求,
;
证明:如图,
;
由作图知:,,
,,
,,
,,
,,
,
,
,
.
24.解:将,代入,
得,
解得:,
抛物线解析式为;
对于,令,则
解得:,
,
,
是等腰直角三角形,
,
,
,
如图所示,过点作交抛物线于点,过点作轴于点,
,
是等腰直角三角形,
,
设,则,
,,
,
解得:舍去或,
;
的面积为定值.
理由:
如图:
设,,
点为中点,,
,
,,三点共线,
可设直线的解析式,
代入得,
直线的解析式,
联立,
得,
,,
,,
同理直线解析式为,直线解析式为,
联立,
解得:,
,
直线解析式,直线解析式为,
,,
,,
,,
,
,
,
,
,
的面积为.
25.解:将正方形纸片沿折叠,使点的对称点落在边上,
,,,
,
∽,
,即,
;
解:是等腰直角三角形,
理由:过作,
翻折,
,,
,
,
,
又,,
≌,
,,
又,
≌,
,
,
,
,
,
是等腰直角三角形;
证明:连接,,,如图,
≌,≌,
,,
,
由折叠可得:,平分,
,,
,,
,
,
,
,
,,,四点共圆,
.
在和中,
,
≌.
,
,
,
,
,
∽,
.
.
.
第1页,共1页
同课章节目录
