江苏省南京秦淮外国语学校2024-2025学年九年级上学期第一次数学月考试题(PDF版,含详解)
文档属性
| 名称 | 江苏省南京秦淮外国语学校2024-2025学年九年级上学期第一次数学月考试题(PDF版,含详解) |  | |
| 格式 | |||
| 文件大小 | 1000.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 19:45:28 | ||
图片预览




文档简介
秦外九上第一次月考试题及答案
一.选择题(共 6 小题)
1.已知圆锥的底面圆半径为 3,母线长为 4,则圆锥的侧面积为 ( )
A. 6 B.12 C.15 D. 24
2.方程 x2 8x 15 0左边配成一个完全平方式后,所得的方程是 ( )
A.(x 4)2 31 B. (x 4)2 1 C.(x 8)2 31 D.(x 8)2 1
3.若关于 x的方程 kx2 2x 1 0有实数根,则实数 k的取值范围是 ( )
A. k 0 B. k 1 C. k 1 D. k 1且 k 0
4.歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,
肯定不会对所有评委打分的哪一个统计量产生影响 ( )
A.平均分 B.众数 C.中位数 D.极差
5.如图所示,等边 ABC的顶点 A在 O上,边 AB、 AC与 O分别交于点 D、 E,点 F 是劣弧D E上
一点,且与 D、 E不重合,连接DF、 EF ,则 DFE 的度数为 ( )
A.115 B.118 C.120 D.125
6.如图,在扇形OAB中,点D在OA上,点C在 AB上, AOB BCD 90 .若CD 3, BC 4,则
O 的半径为 ( )
A.4 B.4.8 C. 2 5 D. 3 2
二.填空题(共 10 小题)
7.若一元二次方程 x2 4x 3 0 的两个根是 x1, x2,则 x1 x2 x1 x2的值是 .
8.已知 O 的圆心坐标为 (3,0),直径为 6,则 O 与 y轴的位置关系是 .
{#{QQABIYWQU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
9.若 (a2 b2 )(a2 b2 2) 3,则a2 b2 .
10 ax 3.关于 x的分式方程 1 0的解为正数,则 a的取值范围是 .
x 2
11.如图所示,点O是 ABC 的内切圆的圆心,若 BAC 76 ,则 BOC的度数为 .
12 1.已知一组数据的方差 s2 [(x1 6)
2 (x2 6)
2 (x3 6)
2 (x 24 6) ],那么这组数据的总和为 .4
13.设函数 y 3 1 1 x 4与 y 的图象的交点坐标为 (m,n),则 的值为 .
x m n
14.如图,正方形 AOBC 的顶点O在原点,边 AO,BO分别在 x轴和 y轴上,点C 坐标为 (4,4),点D是
BO的中点,点 P是边OA上的一个动点,连接 PD,以 P为圆心,PD为半径作圆,设点 P横坐标为 t,
当 P与正方形 AOBC 的边相切时, t的值为 .
15.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如
图所示).若直角三角形的内切圆半径为 3,小正方形的面积为 49,则大正方形的面积为 .
16.如图,在 ABC 中, C 90 , B 30 ,AC 2.点 P在边 AC上,过点 P作 PD AB,垂足为 D,
过点 D作 DF BC,垂足为 F .连接 PF ,取 PF 的中点 E.在点 P从点 A到点C 的运动过程中,点 E所
经过的路径长为 .
{#{QQABIYQWU04ogoAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
三.解答题(共 11 小题)
17.解下列方程:
(1) x2 2x 11 0;
(2) x(x 4) 5(4 x).
2
18 x 1.先化简,再求值: 2 ( x 1);从 1,0,1,2中任选一个代入求值.x 1 x 1
19.射击训练班中的甲、乙两名选手在 5次射击训练中的成绩依次为(单位:环) :
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,请解答下面的问题:
(1) a , b , c ;
(2)教练根据这 5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(3)若选手乙再射击第 6 次,命中的成绩是 8环,则选手乙这 6次射击成绩的方差与前 5次射击成绩的
方差相比会 .(填“变大”、“变小”或“不变” )
{#{QQABIYQWU0o4goAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
20.公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头
盔 4月份到 6月份的销量,该品牌头盔 4月份销售 150个,6月份销售 216个,且从 4月份到 6月份销售
量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为 30元 /个,测算在市场中,当售价为 40元 /个时,月销售量为 600个,若在此
基础上售价每上涨 1元 /个,则月销售量将减少 5个,为使月销售利润达到 8625元,而且尽可能让顾客得
到实惠,则该品牌头盔的实际售价应定为多少元 /个?
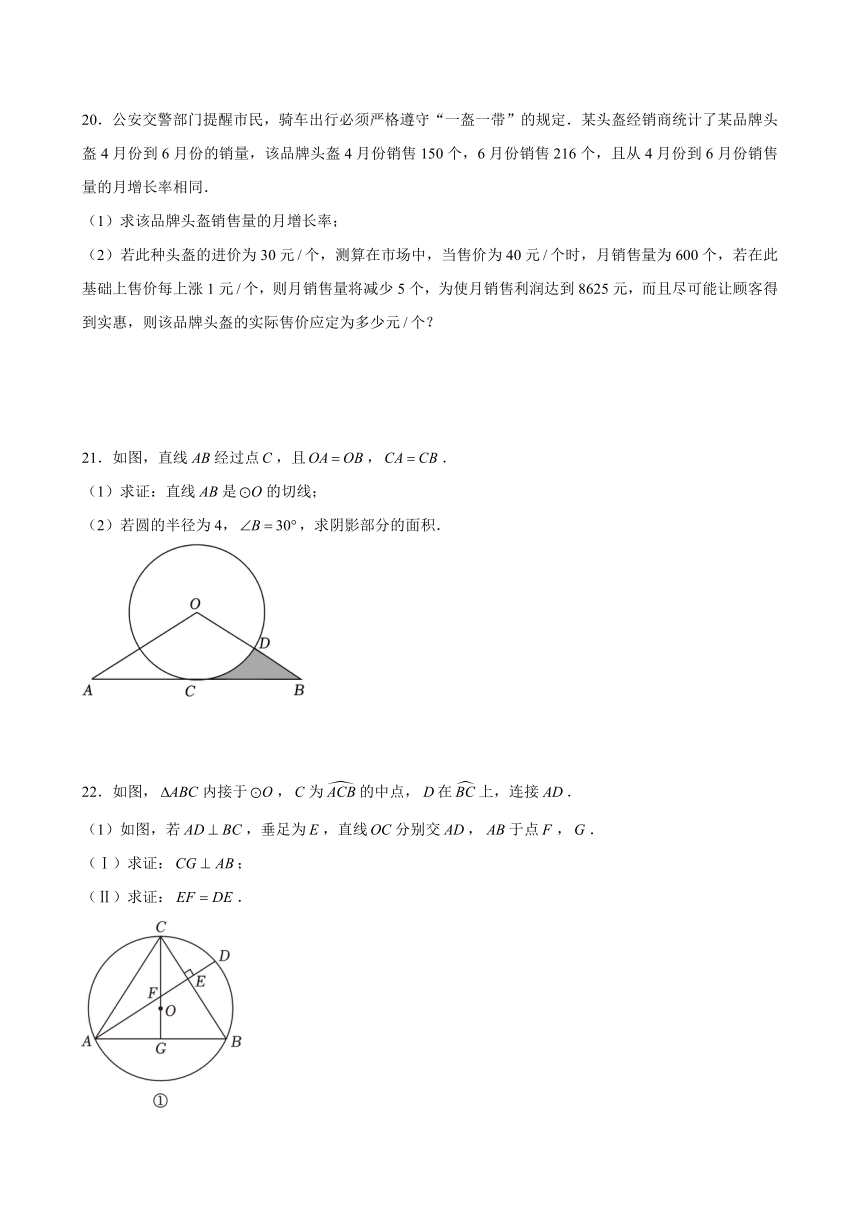
21.如图,直线 AB经过点C,且OA OB,CA CB.
(1)求证:直线 AB是 O的切线;
(2)若圆的半径为 4, B 30 ,求阴影部分的面积.
22.如图, ABC内接于 O ,C为 ACB的中点, D在 B C上,连接 AD.
(1)如图,若 AD BC,垂足为 E,直线OC分别交 AD, AB于点 F ,G.
(Ⅰ)求证:CG AB;
(Ⅱ)求证: EF DE .
{#{QQABIYQWU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
23.在平面直角坐标系 xOy中,点 A、B分别在 x轴负半轴、 y轴正半轴上 (OA OB),C(a, a)(a为常
数),以C为圆心、适当的长度为半径作 C,使点 A、 B在 C上.
(1)请用无刻度的直尺和圆规作出 C.(保留作图痕迹,不写作法);
(2)若OA 8,OB 6,直线 y x b与 C有且只有一个公共点,则 b .
24.若 x m时,代数式 ax2 bx c的值也为m ,则称m是这个代数式的“ x优值”.例如,当 x 0时,
代数式 x2 x的值为 0;当 x 2时,代数式 x2 x的值为 2,所以 0和 2都是 x2 x的“ x优值”.
(1)判断代数式 x2 x n2 2是否存在“ x优值”,并说明理由;
(2)代数式 x2 n2 n存在两个“ x优值”且差为 5,求 n的值.
25.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图 1,等腰直角四边形 ABCD, AB BC. ABC 90 .
①若 AB CD, AB / /CD,请在横线处填出四边形 ABCD是什么特殊的四边形? .
②若 AB BC 2 2 , AD CD 2 5 ,则 S四边形ABCD .
(2)如图 2,矩形 ABCD的长和宽为方程 x2 12x 20 0的两根,其中 (BC AB) .点 E从 A点出发,沿
AD以每秒 1个单位长度的速度向终点 D运动,同时点 F 从C点出发,沿CB以每秒 2个单位长度的速度
向终点 B运动.在点 E, F 的运动过程中,若四边形 ABFE是等腰直角四边形,求 EF 的长.
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
26.如图, O是 ABC的外接圆,CD是 O的切线,且CD / /AB,连接 AD交 O于点 E.
(1)求证 AC BC ;
(2)连接 BE ,若 BE 为直径, BC 3 10 , AE 8,求 O 的半径.
27.【问题情境】
(1)如图 1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面
积的几倍?小昕将小正方形绕圆心旋转 45 (如图 2),这时候就容易发现大正方形面积是小正方形面积的
倍.由此可见,图形变化是解决问题的有效策略;
【操作实践】
(2)如图 3,图①是一个对角线互相垂直的四边形,四边 a、 b、 c、 d之间存在某种数量关系.小昕按
所示步骤进行操作,并将最终图形抽象成图 4.请你结合整个变化过程,直接写出图 4中以矩形内一点 P为
端点的四条线段之间的数量关系;
{#{QQABIYQWU0o4gAoQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
【探究应用】
(3)如图 5,在图 3 中“④”的基础上,小昕将 PDC绕点 P逆时针旋转,他发现旋转过程中 DAP存
在最大值.若 PE 8, PF 5,当 DAP最大时,求 AD的长;
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
秦外九上练习
参考答案与试题解析
一.选择题(共 6 小题)
1.已知圆锥的底面圆半径为 3,母线长为 4,则圆锥的侧面积为 ( )
A. 6 B.12 C.15 D. 24
【解答】解: S侧 rl 3 4 12 ,故选: B.
2.方程 x2 8x 15 0左边配成一个完全平方式后,所得的方程是 ( )
A 2 2 2.(x 4) 31 B. (x 4)2 1 C.(x 8) 31 D.(x 8) 1
【解答】解: x2 8x 15, x2 8x 16 15 16 ,即 (x 4)2 1,故选: B.
3.若关于 x的方程 kx2 2x 1 0有实数根,则实数 k的取值范围是 ( )
A. k 0 B. k 1 C. k 1 D. k 1且 k 0
【解答】解:当 k 0时,△ 4 4k 0, k 1,即 k 1且 k 0,
当 k 0时,此时方程为 2x 1 0,满足题意,
所以 k 1.故选: B.
4.歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,
肯定不会对所有评委打分的哪一个统计量产生影响 ( )
A.平均分 B.众数 C.中位数 D.极差
【解答】解:统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生
影响,即中位数.故选:C.
5.如图所示,等边 ABC的顶点 A在 O上,边 AB、 AC与 O分别交于点 D、 E,点 F 是劣弧D E上
一点,且与 D、 E不重合,连接DF、 EF ,则 DFE 的度数为 ( )
A.115 B.118 C.120 D.125
【解答】解:四边形 EFDA是 O内接四边形, EFD A 180 ,
{#{QQABIYQWU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
等边 ABC的顶点 A在 O上, A 60 , EFD 120 ,故选:C .
6.如图,在扇形OAB中,点D在OA上,点C在 AB上, AOB BCD 90 .若CD 3, BC 4,则
O 的半径为 ( )
A.4 B.4.8 C. 2 5 D. 3 2
【解答】解:以点O为圆心,以OB为半径画圆,延长CD交 O于点 E,连接 BE , BD,如图所示:
在△ BCD中, BCD 90 ,CD 3, BC 4,由勾股定理得: BD BC2 CD2 5,
BCD 90 , BE为 O的直径, 点 B,O, E在同一条直线上, OB OE,
AOB 90 , DE BD 5,
在 Rt△ BCE中,CE CD DE 8, BC 4,由勾股定理得: BE CE2 BC2 82 42 4 5 .
OB OE 1 BE 2 5.故选:C.
2
二.填空题(共 10 小题)
7.若一元二次方程 x2 4x 3 0 的两个根是 x1, x2,则 x1 x2 x1 x2的值是 1 .
【解答】解: x1, x2 是一元二次方程 x
2 4x 3 0的两个根, x1 x2 4, x1 x2 3,
x1 x2 x1 x2 4 3 1,故答案为:1.
8.已知 O 的圆心坐标为 (3,0),直径为 6,则 O 与 y轴的位置关系是 相切 .
【解答】解: O的圆心坐标为 (3,0), 圆心O到 y轴的距离为 3,
O的直径为 6, O的半径为 3, 圆心O到 y轴的距离为等于 O 的半径,
O与 y轴相切.故答案为:相切.
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
9.若 (a2 b2 )(a2 b2 2) 3,则a2 b2 .
2 2 2 2 2 2
【解答】解:令 a b t,则t 0, (a b )(a b 2) t(t 2) t 2 2t 3,
t 2 2t 3 (t 3)(t 1) 0,解得 t1 3, t2 1
2
(舍去).故 a b2 t 3 .
10 ax 3.关于 x的分式方程 1 0的解为正数,则 a的取值范围是 a 1 a 3 且 . .
x 2 2
【解答】解:分式方程去分母得: ax 3 x 2 0,即 (a 1)x 5,
5
当 a 1 0,即 a 1时,解得: x ,
a 1
x 2 5 0 5 2 a 1 a 3分式方程的解为正数且 , 且 ,解得: 且 .
a 1 a 1 2
3
故答案为: a 1且 a .
2
11.如图所示,点O是 ABC 的内切圆的圆心,若 BAC 76 ,则 BOC的度数为 128 .
【解答】解: 点O是 ABC的内切圆的圆心,
BO、CO分别平分 ABC、 ACB, OBC 1 ABC OCB 1 , ACB,
2 2
BAC 76 , ABC ACB 180 BAC 104 ,
BOC 180 ( OBC 1 1 OCB) 180 ( ABC ACB) 180 104 128 .
2 2
故答案为:128 .
12 1.已知一组数据的方差 s2 [(x 6)21 (x2 6)
2 (x 6)2 (x 6)23 4 ],那么这组数据的总和为 24 .4
1
【解答】解: s2 [(x1 6)
2 (x 6)22 (x3 6)
2 (x4 6)
2 ], 这组数据的平均数是 6,数据个数是 4,
4
这组数据的总和为 4 6 24;故答案为:24.
13 3.设函数 y x 4与 y 的图象的交点坐标为 (m,n) 1 1 4,则 的值为 .
x m n 3
【解答】解: 函数 y x 4与 y 3 的图象的交点坐标为 (m,n),
x
{#{QQABIYWQU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
n m 4 mn 3 1 1 n m 4 4 4 , , ,故答案为: .
m n mn 3 3 3
14.如图,正方形 AOBC 的顶点O在原点,边 AO,BO分别在 x轴和 y轴上,点C 坐标为 (4,4),点D是
BO的中点,点 P是边OA上的一个动点,连接 PD,以 P为圆心,PD为半径作圆,设点 P横坐标为 t,
当 P与正方形 AOBC 3的边相切时, t的值为 或 2 3 .
2
【解答】解: 点C 坐标为 (4,4),点 D是 BO的中点, OA OB 4 OD 1 , OB 2.
2
分 P与 AC相切和 P与 BC相切两种情况考虑:
①当 P与 AC相切时,如图 1所示.
点 P横坐标为 t, PA 4 t.
在Rt DOP中,OD 2,OP t , PD PA 4 t,
PD2 OD2 OP2 3,即 (4 t)2 22 t2,解得: t ;
2
②当 P与 BC相切时,设切点为 E,连接 PE,如图 2所示.
PE BC, AC BC, PE / /AC.
PA / /EC, 四边形 ACEP为矩形, PE AC 4, PD PE 4.
在Rt POD中,OP t,OD 2, PD 4,
PD2 OD2 OP2 ,即 42 22 t2 ,解得: t1 2 3, t2 2 3(不合题意,舍去).
t 3 3综上所述: 的值为 或 2 3.故答案为: 或 2 3.
2 2
{#{QQABIYQWU04ogAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
15.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如
图所示).若直角三角形的内切圆半径为 3,小正方形的面积为 49,则大正方形的面积为 289 .
【解答】解:如图,设内切圆的圆心为O,连接OE,OD,
则四边形 EODC为正方形,
OE OD 3 AC BC BA , AC BC AB 6, AC BC AB 6,
2
(AC BC)2 (AB 6)2 , BC 2 AC 2 2BC AC AB2 12AB 36 ,
而 BC 2 AC 2 AB2 , 2BC AC 12AB 36①,
小正方形的面积为 49, (BC AC)2 49, BC 2 AC 2 2BC AC 49②,
把①代入②中得 AB2 12AB 85 0, (AB 17)(AB 5) 0, AB 17(负值舍去),
大正方形的面积为 289.故答案为:289.
16.如图,在 ABC 中, C 90 , B 30 ,AC 2.点 P在边 AC上,过点 P作 PD AB,垂足为 D,
过点 D作 DF BC,垂足为 F .连接 PF ,取 PF 的中点 E.在点 P从点 A到点C 的运动过程中,点 E所
{#{QQABIYWQU04ogoAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
19
经过的路径长为 .
4
【解答】解:方法一:以C为原点,建立坐标系,过点 D作DG AC
设 AP a,则CP 2 a, P(0,2 a),
1 a B 30 , A 60 , PD AB, PDA 90 , APD 30 , AD AP ,
2 2
DG AC, AGD 90 1 a 3 , AG AD , DG 3AG a ,
2 4 4
DF BC,DG AC, ACB 90 , 四边形DGCF 3a为矩形, DG CF , F ( ,0),
4
E 3为 P, F 的中点, E( a,1 1 a),
8 2
3
令 x a, y 1 1 a 4 3 4 3 , y 1 x, 点 E在直线 y 1 x上运动,
8 2 3 3
当点 P与 A重合时, a 0,此时 E(0,1),
当点 P 3与C重合时, a 2,此时 E( ,0),
4
3
点 E所经过的路径长为: 12 ( )2 19 ,
4 4
方法二: P在 AC上运动,运动路径为线段, E为 PF 中点, E 的运动路径亦为线段,
当 P与 A重合时,CE 1,当 P与C重合时,CE 3 ,
4
点 E 3所经过的路径长为: 12 ( )2 19 19 ,故答案为: .
4 4 4
{#{QQABIYWQU04ogoAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
三.解答题(共 11 小题)
17.解下列方程:
(1) x2 2x 11 0;
(2) x(x 4) 5(4 x).
【解答】解:(1) x2 2x 11, x2 2x 1 11 1, (x 1)2 12, x 1 2 3 ,
解得 x1 1 2 3, x2 1 2 3.
(2) x(x 4) 5(x 4) 0, (x 5)(x 4) 0 , x 5 0或 x 4 0,
解得 x1 5, x2 4.
x218 1.先化简,再求值: 2 ( x 1);从 1,0,1,2中任选一个代入求值.x 1 x 1
x2 2
( 1 x 1) x [ 1 (x 1)(x 1) x
2 1 x2 1
【解答】解: 2 ] ( )x 1 x 1 (x 1)(x 1) x 1 x 1 (x 1)(x 1) x 1
x2 x 1 1
,
(x 1)(x 1) x2 x 1
1
根据分式有意义的条件得 x 1且 x 0, x只能为 2,当 x 2时,原式 1.
2 1
19.射击训练班中的甲、乙两名选手在 5次射击训练中的成绩依次为(单位:环) :
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,请解答下面的问题:
(1) a 8 , b , c ;
(2)教练根据这 5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(3)若选手乙再射击第 6 次,命中的成绩是 8环,则选手乙这 6次射击成绩的方差与前 5次射击成绩的
方差相比会 .(填“变大”、“变小”或“不变” )
1
【解答】解:(1)由题可得, a (5 9 7 10 9) 8;
5
甲的成绩 7,8,8,8,9中,8出现的次数最多,故众数 b 8;
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
而乙的成绩 5,7,9,9,10中,中位数 c 9;
故答案为:8,8,9;
(2)教练根据这 5次成绩,决定选择甲参加射击比赛,教练的理由是两人的平均成绩相同,而甲的成绩
的方差小,即甲的成绩较稳定.
(3) 由 题 可 得 , 选 手 乙 这 6 次 射 击 成 绩 5 , 9 , 7 , 10 , 9 , 8 的 方 差
1
[(5 8)2 (9 8)2 (10 8)2 (9 8)2 (8 8)2 ] 2.5 3.2,
6
选手乙这 6次射击成绩的方差与前 5次射击成绩的方差相比会变小.故答案为:变小.
20.公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头
盔 4月份到 6月份的销量,该品牌头盔 4月份销售 150个,6月份销售 216个,且从 4月份到 6月份销售
量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为 30元 /个,测算在市场中,当售价为 40元 /个时,月销售量为 600个,若在此
基础上售价每上涨 1元 /个,则月销售量将减少 5个,为使月销售利润达到 8625元,而且尽可能让顾客得
到实惠,则该品牌头盔的实际售价应定为多少元 /个?
【解答】解:(1)设该品牌头盔销售量的月增长率为 x,依题意,得:150(1 x)2 216,
解得: x1 0.2 20%, x2 2.2(不合题意,舍去).答:该品牌头盔销售量的月增长率为 20%.
(2)设该品牌头盔的实际售价为 y元,
依题意,得: (y 30)[600 5(y 40)] 8625 ,整理,得: y2 190y 6525 0,
解得: y1 145, y2 45, 尽可能让顾客得到实惠, y1 145(不合题意,舍去),
答:该品牌头盔的实际售价应定为 45元.
21.如图,直线 AB经过点C,且OA OB,CA CB.
(1)求证:直线 AB是 O的切线;
(2)若圆的半径为 4, B 30 ,求阴影部分的面积.
{#{QQABIYWQU04ogoAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
【解答】(1)证明:连接OC,
OA OB,CA CB, OC AB, 直线 AB经过点C, OC是 O的半径,
OC是 O的半径,且 AB OC, 直线 AB是 O的切线.
(2)解: OC AB, OCB 90 , O的半径为 4, OC 4,
B 30 , COD 90 BC B 60 , tan 60 3, BC 3OC 4 3 ,
OC
S S 1 60 4
2 8
阴影 OCB S扇形OCD 4 4 3 8 3 ,2 360 3
8 3 8 阴影部分的面积是 .
3
22.如图, ABC内接于 O ,C为 ACB的中点, D在 B C上,连接 AD.
(1)如图,若 AD BC,垂足为 E,直线OC分别交 AD, AB于点 F ,G.
(Ⅰ)求证:CG AB;
(Ⅱ)求证: EF DE .
【解答】(1)(Ⅰ)证明:连接OA、OB,如图,
{#{QQABIYQWU0o4goAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
C 为优弧 AB的中点, AC B C , AC BC,
又OA OB, O、C都在 AB的垂直平分线上,即CG是 AB垂直平分线, CG AB;
(Ⅱ)证明:连接CD,如图,
AD BC,CG AB, CFE BCG 90 , B BCG 90 , B CFE,
B D, CFE D, CF CD.又 AD BC, EF DE;
23.在平面直角坐标系 xOy中,点 A、B分别在 x轴负半轴、 y轴正半轴上 (OA OB),C(a, a)(a为常
数),以C为圆心、适当的长度为半径作 C,使点 A、 B在 C上.
(1)请用无刻度的直尺和圆规作出 C.(保留作图痕迹,不写作法);
(2)若OA 8,OB 6,直线 y x b与 C有且只有一个公共点,则 b 4或 24 .
【解答】解:(1)由点C的坐标知,改点在直线 y x上,由圆的定义知,点C在 AB的中垂线上,
故上述两条直线的交点,即为点C为位置,由此画出 C如图所示.
(2)如图所示,设直线 y x b与 C有且只有一个公共点为点T,
{#{QQABIYQWU04ogAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
则CT 和直线 y x b垂直,且CT AC CB,
点C 在直线 y x, 点T是直线 y x和直线 y x b的交点,
1 1 1 1
则点T ( b, b),由CT AC CB得: (a 8)2 a2 a2 (a 6)2 ( a b)2 (a b)2,
2 2 2 2
解得 b 4或 24.故答案为:4或 24.
24.若 x m时,代数式 ax2 bx c的值也为m ,则称m是这个代数式的“ x优值”.例如,当 x 0时,
代数式 x2 x的值为 0;当 x 2时,代数式 x2 x的值为 2,所以 0和 2都是 x2 x的“ x优值”.
(1)判断代数式 x2 x n2 2是否存在“ x优值”,并说明理由;
(2)代数式 x2 n2 n存在两个“ x优值”且差为 5,求 n的值.
【解答】解:(1)不存在“ x优值”.理由如下:
假设存在优值为 x,则有 x2 x n2 2 x,整理得: x2 2x n2 2 0,
则 b2 4ac 22 4(n2 2) 4n2 4, 无论 n取何值时, 4n2 4 0, 方程没有实数根,
即代数式 x2 x n2 2不存在“ x优值”.
(2)设“ x优值”为 x,则有 x2 n2 n x,整理得: x2 x n(n 1) 0,
(x n)(x n 1) 0, x1 n, x2 1 n.
两个“ x优值”差为 5, n (1 n) 5或 (1 n) n 5, n 3或 n 2.
25.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图 1,等腰直角四边形 ABCD, AB BC. ABC 90 .
①若 AB CD, AB / /CD,请在横线处填出四边形 ABCD是什么特殊的四边形? 正方形 .
②若 AB BC 2 2 , AD CD 2 5 ,则 S四边形ABCD .
(2)如图 2,矩形 ABCD的长和宽为方程 x2 12x 20 0的两根,其中 (BC AB) .点 E从 A点出发,沿
AD以每秒 1个单位长度的速度向终点 D运动,同时点 F 从C点出发,沿CB以每秒 2个单位长度的速度
向终点 B运动.在点 E, F 的运动过程中,若四边形 ABFE是等腰直角四边形,求 EF 的长.
{#{QQABIYWQU04ogAoQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
【解答】(1)①解: AB CD, AB / /CD, 四边形 ABCD为平行四边形,
AB BC, 四边形 ABCD为菱形, ABC 90 , 四边形 ABCD为正方形,
故答案为:正方形;
②证明:连接 AC、 BD,如图所示:
AB BC 2 2, AD CD 2 5 , BD垂直平分 AC, AC 4,
AO OC 2 BO, DO CD2 CO2 20 4 4 1, BD 6, S四边形ABCD 4 6 12,2
故答案为:12;
(2)解: x2 12x 20 0 0, (x 10)(x 2) 0, x 10 0或 x 2 0,
解得: x1 10, x2 2, BC AB, AD BC 10,CD AB 2,
根据题意可知,当 AB AE或 AB BF 时,四边形 ABFE是等腰直角四边形;
当 AB AE 2时,连接 EF ,过点 E作 EH BC于点H ,如图所示:
AE
运动时间为: 2(秒 ), CF 2 2 4, BF 10 4 6,
1
A B AGF 90 , 四边形 ABFG为矩形, BH AE 2, EH AB 2,
HF BF BH 6 2 4, EF EH 2 HF 2 4 16 2 5;
当 AB BF 2时,连接 EF ,过点 F 作 FG BC 于点G,如图所示:
{#{QQABIYWQU04ogoAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
——
则CF BC BF 10 2 8 8,此时运动时间为: t 4, AE 4,
2
A B BHE 90 , 四边形 ABHE矩形, AG BF 2,GF AB 2,
GE 4 2 2, EF GF 2 GE2 4 4 2 2;综上分析可知, EF 2 5 或 2 2.
26.如图, O是 ABC的外接圆,CD是 O的切线,且CD / /AB,连接 AD交 O于点 E.
(1)求证 AC BC ;
(2)连接 BE ,若 BE 为直径, BC 3 10 , AE 8,求 O 的半径.
【解答】(1)证明:连接CO并延长交 AB于点 F ,连接 BE,
CD是 O的切线, OCD 90 ,
CD / /AB, OFB OCD 90 ,即OF AB, AF BF , CF 是 AB的垂直平分线, AC BC;
(2)解: AF BF ,OB OE, OF 1 1 AE 8 4,
2 2
设OB OC r ,在Rt BCF和Rt BOF中,由勾股定理得: BF 2 CF 2 BC 2 , BF 2 OF 2 OB2 ,
即 BF 2 (3 10)2 (r 4)2 , BF 2 r2 42, (3 10)2 (r 4)2 r2 42 ,
解得 r1 5. r2 9 (舍去). O的半径为 5.
{#{QQABIYQWU04ogAoQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
27.【问题情境】
(1)如图 1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面
积的几倍?小昕将小正方形绕圆心旋转 45 (如图 2),这时候就容易发现大正方形面积是小正方形面积的
2 倍.由此可见,图形变化是解决问题的有效策略;
【操作实践】
(2)如图 3,图①是一个对角线互相垂直的四边形,四边 a、 b、 c、 d之间存在某种数量关系.小昕按
所示步骤进行操作,并将最终图形抽象成图 4.请你结合整个变化过程,直接写出图 4中以矩形内一点 P为
端点的四条线段之间的数量关系;
【探究应用】
(3)如图 5,在图 3 中“④”的基础上,小昕将 PDC绕点 P逆时针旋转,他发现旋转过程中 DAP存
在最大值.若 PE 8, PF 5,当 DAP最大时,求 AD的长;
【解答】解:(1) 正方形 ABCD,EFGH及圆为正方形 ABCD的内切圆,为正方形 EFGH的外接正方形,
设 AE DE DH CH CG BG AF BF m, A 90 ,
AB AD 2m, EF m2 m2 2m, S 2正方形ABCD 4m , S正方形EFGH ( 2m)
2 2m2,
大正方形面积是小正方形面积的 2倍,故答案为:2;
{#{QQABIYWQU04ogAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
(2)如图,
EG FH, a2 OF 2 OE 2 , c2 OG2 OH 2 , d 2 OE 2 OH 2 ,b2 OF 2 OG2 ,
a2 c2 b2 d 2 ,结合图形变换可得: PA2 PC 2 PB2 PD2 ;
(3)如图, 将 PDC绕点 P逆时针旋转,
点D在以点 P为圆心, PD为半径的圆上运动,
A为圆外一个定点, 当 AD与 P相切时, DAP最大, PD AD,
AD2 AP2 PD2 ,由(2)可得: AE DF,
PE 8, PF 5, AD2 AP2 PD2 PE 2 AE 2 PF 2 DF 2 82 52 39, AD 39 ;6 20:07:51;用户: 15365143975;邮箱:15365143975;学号: 51233
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
一.选择题(共 6 小题)
1.已知圆锥的底面圆半径为 3,母线长为 4,则圆锥的侧面积为 ( )
A. 6 B.12 C.15 D. 24
2.方程 x2 8x 15 0左边配成一个完全平方式后,所得的方程是 ( )
A.(x 4)2 31 B. (x 4)2 1 C.(x 8)2 31 D.(x 8)2 1
3.若关于 x的方程 kx2 2x 1 0有实数根,则实数 k的取值范围是 ( )
A. k 0 B. k 1 C. k 1 D. k 1且 k 0
4.歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,
肯定不会对所有评委打分的哪一个统计量产生影响 ( )
A.平均分 B.众数 C.中位数 D.极差
5.如图所示,等边 ABC的顶点 A在 O上,边 AB、 AC与 O分别交于点 D、 E,点 F 是劣弧D E上
一点,且与 D、 E不重合,连接DF、 EF ,则 DFE 的度数为 ( )
A.115 B.118 C.120 D.125
6.如图,在扇形OAB中,点D在OA上,点C在 AB上, AOB BCD 90 .若CD 3, BC 4,则
O 的半径为 ( )
A.4 B.4.8 C. 2 5 D. 3 2
二.填空题(共 10 小题)
7.若一元二次方程 x2 4x 3 0 的两个根是 x1, x2,则 x1 x2 x1 x2的值是 .
8.已知 O 的圆心坐标为 (3,0),直径为 6,则 O 与 y轴的位置关系是 .
{#{QQABIYWQU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
9.若 (a2 b2 )(a2 b2 2) 3,则a2 b2 .
10 ax 3.关于 x的分式方程 1 0的解为正数,则 a的取值范围是 .
x 2
11.如图所示,点O是 ABC 的内切圆的圆心,若 BAC 76 ,则 BOC的度数为 .
12 1.已知一组数据的方差 s2 [(x1 6)
2 (x2 6)
2 (x3 6)
2 (x 24 6) ],那么这组数据的总和为 .4
13.设函数 y 3 1 1 x 4与 y 的图象的交点坐标为 (m,n),则 的值为 .
x m n
14.如图,正方形 AOBC 的顶点O在原点,边 AO,BO分别在 x轴和 y轴上,点C 坐标为 (4,4),点D是
BO的中点,点 P是边OA上的一个动点,连接 PD,以 P为圆心,PD为半径作圆,设点 P横坐标为 t,
当 P与正方形 AOBC 的边相切时, t的值为 .
15.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如
图所示).若直角三角形的内切圆半径为 3,小正方形的面积为 49,则大正方形的面积为 .
16.如图,在 ABC 中, C 90 , B 30 ,AC 2.点 P在边 AC上,过点 P作 PD AB,垂足为 D,
过点 D作 DF BC,垂足为 F .连接 PF ,取 PF 的中点 E.在点 P从点 A到点C 的运动过程中,点 E所
经过的路径长为 .
{#{QQABIYQWU04ogoAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
三.解答题(共 11 小题)
17.解下列方程:
(1) x2 2x 11 0;
(2) x(x 4) 5(4 x).
2
18 x 1.先化简,再求值: 2 ( x 1);从 1,0,1,2中任选一个代入求值.x 1 x 1
19.射击训练班中的甲、乙两名选手在 5次射击训练中的成绩依次为(单位:环) :
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,请解答下面的问题:
(1) a , b , c ;
(2)教练根据这 5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(3)若选手乙再射击第 6 次,命中的成绩是 8环,则选手乙这 6次射击成绩的方差与前 5次射击成绩的
方差相比会 .(填“变大”、“变小”或“不变” )
{#{QQABIYQWU0o4goAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
20.公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头
盔 4月份到 6月份的销量,该品牌头盔 4月份销售 150个,6月份销售 216个,且从 4月份到 6月份销售
量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为 30元 /个,测算在市场中,当售价为 40元 /个时,月销售量为 600个,若在此
基础上售价每上涨 1元 /个,则月销售量将减少 5个,为使月销售利润达到 8625元,而且尽可能让顾客得
到实惠,则该品牌头盔的实际售价应定为多少元 /个?
21.如图,直线 AB经过点C,且OA OB,CA CB.
(1)求证:直线 AB是 O的切线;
(2)若圆的半径为 4, B 30 ,求阴影部分的面积.
22.如图, ABC内接于 O ,C为 ACB的中点, D在 B C上,连接 AD.
(1)如图,若 AD BC,垂足为 E,直线OC分别交 AD, AB于点 F ,G.
(Ⅰ)求证:CG AB;
(Ⅱ)求证: EF DE .
{#{QQABIYQWU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
23.在平面直角坐标系 xOy中,点 A、B分别在 x轴负半轴、 y轴正半轴上 (OA OB),C(a, a)(a为常
数),以C为圆心、适当的长度为半径作 C,使点 A、 B在 C上.
(1)请用无刻度的直尺和圆规作出 C.(保留作图痕迹,不写作法);
(2)若OA 8,OB 6,直线 y x b与 C有且只有一个公共点,则 b .
24.若 x m时,代数式 ax2 bx c的值也为m ,则称m是这个代数式的“ x优值”.例如,当 x 0时,
代数式 x2 x的值为 0;当 x 2时,代数式 x2 x的值为 2,所以 0和 2都是 x2 x的“ x优值”.
(1)判断代数式 x2 x n2 2是否存在“ x优值”,并说明理由;
(2)代数式 x2 n2 n存在两个“ x优值”且差为 5,求 n的值.
25.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图 1,等腰直角四边形 ABCD, AB BC. ABC 90 .
①若 AB CD, AB / /CD,请在横线处填出四边形 ABCD是什么特殊的四边形? .
②若 AB BC 2 2 , AD CD 2 5 ,则 S四边形ABCD .
(2)如图 2,矩形 ABCD的长和宽为方程 x2 12x 20 0的两根,其中 (BC AB) .点 E从 A点出发,沿
AD以每秒 1个单位长度的速度向终点 D运动,同时点 F 从C点出发,沿CB以每秒 2个单位长度的速度
向终点 B运动.在点 E, F 的运动过程中,若四边形 ABFE是等腰直角四边形,求 EF 的长.
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
26.如图, O是 ABC的外接圆,CD是 O的切线,且CD / /AB,连接 AD交 O于点 E.
(1)求证 AC BC ;
(2)连接 BE ,若 BE 为直径, BC 3 10 , AE 8,求 O 的半径.
27.【问题情境】
(1)如图 1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面
积的几倍?小昕将小正方形绕圆心旋转 45 (如图 2),这时候就容易发现大正方形面积是小正方形面积的
倍.由此可见,图形变化是解决问题的有效策略;
【操作实践】
(2)如图 3,图①是一个对角线互相垂直的四边形,四边 a、 b、 c、 d之间存在某种数量关系.小昕按
所示步骤进行操作,并将最终图形抽象成图 4.请你结合整个变化过程,直接写出图 4中以矩形内一点 P为
端点的四条线段之间的数量关系;
{#{QQABIYQWU0o4gAoQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
【探究应用】
(3)如图 5,在图 3 中“④”的基础上,小昕将 PDC绕点 P逆时针旋转,他发现旋转过程中 DAP存
在最大值.若 PE 8, PF 5,当 DAP最大时,求 AD的长;
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
秦外九上练习
参考答案与试题解析
一.选择题(共 6 小题)
1.已知圆锥的底面圆半径为 3,母线长为 4,则圆锥的侧面积为 ( )
A. 6 B.12 C.15 D. 24
【解答】解: S侧 rl 3 4 12 ,故选: B.
2.方程 x2 8x 15 0左边配成一个完全平方式后,所得的方程是 ( )
A 2 2 2.(x 4) 31 B. (x 4)2 1 C.(x 8) 31 D.(x 8) 1
【解答】解: x2 8x 15, x2 8x 16 15 16 ,即 (x 4)2 1,故选: B.
3.若关于 x的方程 kx2 2x 1 0有实数根,则实数 k的取值范围是 ( )
A. k 0 B. k 1 C. k 1 D. k 1且 k 0
【解答】解:当 k 0时,△ 4 4k 0, k 1,即 k 1且 k 0,
当 k 0时,此时方程为 2x 1 0,满足题意,
所以 k 1.故选: B.
4.歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,
肯定不会对所有评委打分的哪一个统计量产生影响 ( )
A.平均分 B.众数 C.中位数 D.极差
【解答】解:统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生
影响,即中位数.故选:C.
5.如图所示,等边 ABC的顶点 A在 O上,边 AB、 AC与 O分别交于点 D、 E,点 F 是劣弧D E上
一点,且与 D、 E不重合,连接DF、 EF ,则 DFE 的度数为 ( )
A.115 B.118 C.120 D.125
【解答】解:四边形 EFDA是 O内接四边形, EFD A 180 ,
{#{QQABIYQWU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
等边 ABC的顶点 A在 O上, A 60 , EFD 120 ,故选:C .
6.如图,在扇形OAB中,点D在OA上,点C在 AB上, AOB BCD 90 .若CD 3, BC 4,则
O 的半径为 ( )
A.4 B.4.8 C. 2 5 D. 3 2
【解答】解:以点O为圆心,以OB为半径画圆,延长CD交 O于点 E,连接 BE , BD,如图所示:
在△ BCD中, BCD 90 ,CD 3, BC 4,由勾股定理得: BD BC2 CD2 5,
BCD 90 , BE为 O的直径, 点 B,O, E在同一条直线上, OB OE,
AOB 90 , DE BD 5,
在 Rt△ BCE中,CE CD DE 8, BC 4,由勾股定理得: BE CE2 BC2 82 42 4 5 .
OB OE 1 BE 2 5.故选:C.
2
二.填空题(共 10 小题)
7.若一元二次方程 x2 4x 3 0 的两个根是 x1, x2,则 x1 x2 x1 x2的值是 1 .
【解答】解: x1, x2 是一元二次方程 x
2 4x 3 0的两个根, x1 x2 4, x1 x2 3,
x1 x2 x1 x2 4 3 1,故答案为:1.
8.已知 O 的圆心坐标为 (3,0),直径为 6,则 O 与 y轴的位置关系是 相切 .
【解答】解: O的圆心坐标为 (3,0), 圆心O到 y轴的距离为 3,
O的直径为 6, O的半径为 3, 圆心O到 y轴的距离为等于 O 的半径,
O与 y轴相切.故答案为:相切.
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
9.若 (a2 b2 )(a2 b2 2) 3,则a2 b2 .
2 2 2 2 2 2
【解答】解:令 a b t,则t 0, (a b )(a b 2) t(t 2) t 2 2t 3,
t 2 2t 3 (t 3)(t 1) 0,解得 t1 3, t2 1
2
(舍去).故 a b2 t 3 .
10 ax 3.关于 x的分式方程 1 0的解为正数,则 a的取值范围是 a 1 a 3 且 . .
x 2 2
【解答】解:分式方程去分母得: ax 3 x 2 0,即 (a 1)x 5,
5
当 a 1 0,即 a 1时,解得: x ,
a 1
x 2 5 0 5 2 a 1 a 3分式方程的解为正数且 , 且 ,解得: 且 .
a 1 a 1 2
3
故答案为: a 1且 a .
2
11.如图所示,点O是 ABC 的内切圆的圆心,若 BAC 76 ,则 BOC的度数为 128 .
【解答】解: 点O是 ABC的内切圆的圆心,
BO、CO分别平分 ABC、 ACB, OBC 1 ABC OCB 1 , ACB,
2 2
BAC 76 , ABC ACB 180 BAC 104 ,
BOC 180 ( OBC 1 1 OCB) 180 ( ABC ACB) 180 104 128 .
2 2
故答案为:128 .
12 1.已知一组数据的方差 s2 [(x 6)21 (x2 6)
2 (x 6)2 (x 6)23 4 ],那么这组数据的总和为 24 .4
1
【解答】解: s2 [(x1 6)
2 (x 6)22 (x3 6)
2 (x4 6)
2 ], 这组数据的平均数是 6,数据个数是 4,
4
这组数据的总和为 4 6 24;故答案为:24.
13 3.设函数 y x 4与 y 的图象的交点坐标为 (m,n) 1 1 4,则 的值为 .
x m n 3
【解答】解: 函数 y x 4与 y 3 的图象的交点坐标为 (m,n),
x
{#{QQABIYWQU0o4gAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
n m 4 mn 3 1 1 n m 4 4 4 , , ,故答案为: .
m n mn 3 3 3
14.如图,正方形 AOBC 的顶点O在原点,边 AO,BO分别在 x轴和 y轴上,点C 坐标为 (4,4),点D是
BO的中点,点 P是边OA上的一个动点,连接 PD,以 P为圆心,PD为半径作圆,设点 P横坐标为 t,
当 P与正方形 AOBC 3的边相切时, t的值为 或 2 3 .
2
【解答】解: 点C 坐标为 (4,4),点 D是 BO的中点, OA OB 4 OD 1 , OB 2.
2
分 P与 AC相切和 P与 BC相切两种情况考虑:
①当 P与 AC相切时,如图 1所示.
点 P横坐标为 t, PA 4 t.
在Rt DOP中,OD 2,OP t , PD PA 4 t,
PD2 OD2 OP2 3,即 (4 t)2 22 t2,解得: t ;
2
②当 P与 BC相切时,设切点为 E,连接 PE,如图 2所示.
PE BC, AC BC, PE / /AC.
PA / /EC, 四边形 ACEP为矩形, PE AC 4, PD PE 4.
在Rt POD中,OP t,OD 2, PD 4,
PD2 OD2 OP2 ,即 42 22 t2 ,解得: t1 2 3, t2 2 3(不合题意,舍去).
t 3 3综上所述: 的值为 或 2 3.故答案为: 或 2 3.
2 2
{#{QQABIYQWU04ogAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
15.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如
图所示).若直角三角形的内切圆半径为 3,小正方形的面积为 49,则大正方形的面积为 289 .
【解答】解:如图,设内切圆的圆心为O,连接OE,OD,
则四边形 EODC为正方形,
OE OD 3 AC BC BA , AC BC AB 6, AC BC AB 6,
2
(AC BC)2 (AB 6)2 , BC 2 AC 2 2BC AC AB2 12AB 36 ,
而 BC 2 AC 2 AB2 , 2BC AC 12AB 36①,
小正方形的面积为 49, (BC AC)2 49, BC 2 AC 2 2BC AC 49②,
把①代入②中得 AB2 12AB 85 0, (AB 17)(AB 5) 0, AB 17(负值舍去),
大正方形的面积为 289.故答案为:289.
16.如图,在 ABC 中, C 90 , B 30 ,AC 2.点 P在边 AC上,过点 P作 PD AB,垂足为 D,
过点 D作 DF BC,垂足为 F .连接 PF ,取 PF 的中点 E.在点 P从点 A到点C 的运动过程中,点 E所
{#{QQABIYWQU04ogoAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
19
经过的路径长为 .
4
【解答】解:方法一:以C为原点,建立坐标系,过点 D作DG AC
设 AP a,则CP 2 a, P(0,2 a),
1 a B 30 , A 60 , PD AB, PDA 90 , APD 30 , AD AP ,
2 2
DG AC, AGD 90 1 a 3 , AG AD , DG 3AG a ,
2 4 4
DF BC,DG AC, ACB 90 , 四边形DGCF 3a为矩形, DG CF , F ( ,0),
4
E 3为 P, F 的中点, E( a,1 1 a),
8 2
3
令 x a, y 1 1 a 4 3 4 3 , y 1 x, 点 E在直线 y 1 x上运动,
8 2 3 3
当点 P与 A重合时, a 0,此时 E(0,1),
当点 P 3与C重合时, a 2,此时 E( ,0),
4
3
点 E所经过的路径长为: 12 ( )2 19 ,
4 4
方法二: P在 AC上运动,运动路径为线段, E为 PF 中点, E 的运动路径亦为线段,
当 P与 A重合时,CE 1,当 P与C重合时,CE 3 ,
4
点 E 3所经过的路径长为: 12 ( )2 19 19 ,故答案为: .
4 4 4
{#{QQABIYWQU04ogoAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
三.解答题(共 11 小题)
17.解下列方程:
(1) x2 2x 11 0;
(2) x(x 4) 5(4 x).
【解答】解:(1) x2 2x 11, x2 2x 1 11 1, (x 1)2 12, x 1 2 3 ,
解得 x1 1 2 3, x2 1 2 3.
(2) x(x 4) 5(x 4) 0, (x 5)(x 4) 0 , x 5 0或 x 4 0,
解得 x1 5, x2 4.
x218 1.先化简,再求值: 2 ( x 1);从 1,0,1,2中任选一个代入求值.x 1 x 1
x2 2
( 1 x 1) x [ 1 (x 1)(x 1) x
2 1 x2 1
【解答】解: 2 ] ( )x 1 x 1 (x 1)(x 1) x 1 x 1 (x 1)(x 1) x 1
x2 x 1 1
,
(x 1)(x 1) x2 x 1
1
根据分式有意义的条件得 x 1且 x 0, x只能为 2,当 x 2时,原式 1.
2 1
19.射击训练班中的甲、乙两名选手在 5次射击训练中的成绩依次为(单位:环) :
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,请解答下面的问题:
(1) a 8 , b , c ;
(2)教练根据这 5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(3)若选手乙再射击第 6 次,命中的成绩是 8环,则选手乙这 6次射击成绩的方差与前 5次射击成绩的
方差相比会 .(填“变大”、“变小”或“不变” )
1
【解答】解:(1)由题可得, a (5 9 7 10 9) 8;
5
甲的成绩 7,8,8,8,9中,8出现的次数最多,故众数 b 8;
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
而乙的成绩 5,7,9,9,10中,中位数 c 9;
故答案为:8,8,9;
(2)教练根据这 5次成绩,决定选择甲参加射击比赛,教练的理由是两人的平均成绩相同,而甲的成绩
的方差小,即甲的成绩较稳定.
(3) 由 题 可 得 , 选 手 乙 这 6 次 射 击 成 绩 5 , 9 , 7 , 10 , 9 , 8 的 方 差
1
[(5 8)2 (9 8)2 (10 8)2 (9 8)2 (8 8)2 ] 2.5 3.2,
6
选手乙这 6次射击成绩的方差与前 5次射击成绩的方差相比会变小.故答案为:变小.
20.公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头
盔 4月份到 6月份的销量,该品牌头盔 4月份销售 150个,6月份销售 216个,且从 4月份到 6月份销售
量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为 30元 /个,测算在市场中,当售价为 40元 /个时,月销售量为 600个,若在此
基础上售价每上涨 1元 /个,则月销售量将减少 5个,为使月销售利润达到 8625元,而且尽可能让顾客得
到实惠,则该品牌头盔的实际售价应定为多少元 /个?
【解答】解:(1)设该品牌头盔销售量的月增长率为 x,依题意,得:150(1 x)2 216,
解得: x1 0.2 20%, x2 2.2(不合题意,舍去).答:该品牌头盔销售量的月增长率为 20%.
(2)设该品牌头盔的实际售价为 y元,
依题意,得: (y 30)[600 5(y 40)] 8625 ,整理,得: y2 190y 6525 0,
解得: y1 145, y2 45, 尽可能让顾客得到实惠, y1 145(不合题意,舍去),
答:该品牌头盔的实际售价应定为 45元.
21.如图,直线 AB经过点C,且OA OB,CA CB.
(1)求证:直线 AB是 O的切线;
(2)若圆的半径为 4, B 30 ,求阴影部分的面积.
{#{QQABIYWQU04ogoAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
【解答】(1)证明:连接OC,
OA OB,CA CB, OC AB, 直线 AB经过点C, OC是 O的半径,
OC是 O的半径,且 AB OC, 直线 AB是 O的切线.
(2)解: OC AB, OCB 90 , O的半径为 4, OC 4,
B 30 , COD 90 BC B 60 , tan 60 3, BC 3OC 4 3 ,
OC
S S 1 60 4
2 8
阴影 OCB S扇形OCD 4 4 3 8 3 ,2 360 3
8 3 8 阴影部分的面积是 .
3
22.如图, ABC内接于 O ,C为 ACB的中点, D在 B C上,连接 AD.
(1)如图,若 AD BC,垂足为 E,直线OC分别交 AD, AB于点 F ,G.
(Ⅰ)求证:CG AB;
(Ⅱ)求证: EF DE .
【解答】(1)(Ⅰ)证明:连接OA、OB,如图,
{#{QQABIYQWU0o4goAQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
C 为优弧 AB的中点, AC B C , AC BC,
又OA OB, O、C都在 AB的垂直平分线上,即CG是 AB垂直平分线, CG AB;
(Ⅱ)证明:连接CD,如图,
AD BC,CG AB, CFE BCG 90 , B BCG 90 , B CFE,
B D, CFE D, CF CD.又 AD BC, EF DE;
23.在平面直角坐标系 xOy中,点 A、B分别在 x轴负半轴、 y轴正半轴上 (OA OB),C(a, a)(a为常
数),以C为圆心、适当的长度为半径作 C,使点 A、 B在 C上.
(1)请用无刻度的直尺和圆规作出 C.(保留作图痕迹,不写作法);
(2)若OA 8,OB 6,直线 y x b与 C有且只有一个公共点,则 b 4或 24 .
【解答】解:(1)由点C的坐标知,改点在直线 y x上,由圆的定义知,点C在 AB的中垂线上,
故上述两条直线的交点,即为点C为位置,由此画出 C如图所示.
(2)如图所示,设直线 y x b与 C有且只有一个公共点为点T,
{#{QQABIYQWU04ogAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
则CT 和直线 y x b垂直,且CT AC CB,
点C 在直线 y x, 点T是直线 y x和直线 y x b的交点,
1 1 1 1
则点T ( b, b),由CT AC CB得: (a 8)2 a2 a2 (a 6)2 ( a b)2 (a b)2,
2 2 2 2
解得 b 4或 24.故答案为:4或 24.
24.若 x m时,代数式 ax2 bx c的值也为m ,则称m是这个代数式的“ x优值”.例如,当 x 0时,
代数式 x2 x的值为 0;当 x 2时,代数式 x2 x的值为 2,所以 0和 2都是 x2 x的“ x优值”.
(1)判断代数式 x2 x n2 2是否存在“ x优值”,并说明理由;
(2)代数式 x2 n2 n存在两个“ x优值”且差为 5,求 n的值.
【解答】解:(1)不存在“ x优值”.理由如下:
假设存在优值为 x,则有 x2 x n2 2 x,整理得: x2 2x n2 2 0,
则 b2 4ac 22 4(n2 2) 4n2 4, 无论 n取何值时, 4n2 4 0, 方程没有实数根,
即代数式 x2 x n2 2不存在“ x优值”.
(2)设“ x优值”为 x,则有 x2 n2 n x,整理得: x2 x n(n 1) 0,
(x n)(x n 1) 0, x1 n, x2 1 n.
两个“ x优值”差为 5, n (1 n) 5或 (1 n) n 5, n 3或 n 2.
25.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图 1,等腰直角四边形 ABCD, AB BC. ABC 90 .
①若 AB CD, AB / /CD,请在横线处填出四边形 ABCD是什么特殊的四边形? 正方形 .
②若 AB BC 2 2 , AD CD 2 5 ,则 S四边形ABCD .
(2)如图 2,矩形 ABCD的长和宽为方程 x2 12x 20 0的两根,其中 (BC AB) .点 E从 A点出发,沿
AD以每秒 1个单位长度的速度向终点 D运动,同时点 F 从C点出发,沿CB以每秒 2个单位长度的速度
向终点 B运动.在点 E, F 的运动过程中,若四边形 ABFE是等腰直角四边形,求 EF 的长.
{#{QQABIYWQU04ogAoQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
【解答】(1)①解: AB CD, AB / /CD, 四边形 ABCD为平行四边形,
AB BC, 四边形 ABCD为菱形, ABC 90 , 四边形 ABCD为正方形,
故答案为:正方形;
②证明:连接 AC、 BD,如图所示:
AB BC 2 2, AD CD 2 5 , BD垂直平分 AC, AC 4,
AO OC 2 BO, DO CD2 CO2 20 4 4 1, BD 6, S四边形ABCD 4 6 12,2
故答案为:12;
(2)解: x2 12x 20 0 0, (x 10)(x 2) 0, x 10 0或 x 2 0,
解得: x1 10, x2 2, BC AB, AD BC 10,CD AB 2,
根据题意可知,当 AB AE或 AB BF 时,四边形 ABFE是等腰直角四边形;
当 AB AE 2时,连接 EF ,过点 E作 EH BC于点H ,如图所示:
AE
运动时间为: 2(秒 ), CF 2 2 4, BF 10 4 6,
1
A B AGF 90 , 四边形 ABFG为矩形, BH AE 2, EH AB 2,
HF BF BH 6 2 4, EF EH 2 HF 2 4 16 2 5;
当 AB BF 2时,连接 EF ,过点 F 作 FG BC 于点G,如图所示:
{#{QQABIYWQU04ogoAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
——
则CF BC BF 10 2 8 8,此时运动时间为: t 4, AE 4,
2
A B BHE 90 , 四边形 ABHE矩形, AG BF 2,GF AB 2,
GE 4 2 2, EF GF 2 GE2 4 4 2 2;综上分析可知, EF 2 5 或 2 2.
26.如图, O是 ABC的外接圆,CD是 O的切线,且CD / /AB,连接 AD交 O于点 E.
(1)求证 AC BC ;
(2)连接 BE ,若 BE 为直径, BC 3 10 , AE 8,求 O 的半径.
【解答】(1)证明:连接CO并延长交 AB于点 F ,连接 BE,
CD是 O的切线, OCD 90 ,
CD / /AB, OFB OCD 90 ,即OF AB, AF BF , CF 是 AB的垂直平分线, AC BC;
(2)解: AF BF ,OB OE, OF 1 1 AE 8 4,
2 2
设OB OC r ,在Rt BCF和Rt BOF中,由勾股定理得: BF 2 CF 2 BC 2 , BF 2 OF 2 OB2 ,
即 BF 2 (3 10)2 (r 4)2 , BF 2 r2 42, (3 10)2 (r 4)2 r2 42 ,
解得 r1 5. r2 9 (舍去). O的半径为 5.
{#{QQABIYQWU04ogAoQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
27.【问题情境】
(1)如图 1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面
积的几倍?小昕将小正方形绕圆心旋转 45 (如图 2),这时候就容易发现大正方形面积是小正方形面积的
2 倍.由此可见,图形变化是解决问题的有效策略;
【操作实践】
(2)如图 3,图①是一个对角线互相垂直的四边形,四边 a、 b、 c、 d之间存在某种数量关系.小昕按
所示步骤进行操作,并将最终图形抽象成图 4.请你结合整个变化过程,直接写出图 4中以矩形内一点 P为
端点的四条线段之间的数量关系;
【探究应用】
(3)如图 5,在图 3 中“④”的基础上,小昕将 PDC绕点 P逆时针旋转,他发现旋转过程中 DAP存
在最大值.若 PE 8, PF 5,当 DAP最大时,求 AD的长;
【解答】解:(1) 正方形 ABCD,EFGH及圆为正方形 ABCD的内切圆,为正方形 EFGH的外接正方形,
设 AE DE DH CH CG BG AF BF m, A 90 ,
AB AD 2m, EF m2 m2 2m, S 2正方形ABCD 4m , S正方形EFGH ( 2m)
2 2m2,
大正方形面积是小正方形面积的 2倍,故答案为:2;
{#{QQABIYWQU04ogAoQgAgIJTAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
(2)如图,
EG FH, a2 OF 2 OE 2 , c2 OG2 OH 2 , d 2 OE 2 OH 2 ,b2 OF 2 OG2 ,
a2 c2 b2 d 2 ,结合图形变换可得: PA2 PC 2 PB2 PD2 ;
(3)如图, 将 PDC绕点 P逆时针旋转,
点D在以点 P为圆心, PD为半径的圆上运动,
A为圆外一个定点, 当 AD与 P相切时, DAP最大, PD AD,
AD2 AP2 PD2 ,由(2)可得: AE DF,
PE 8, PF 5, AD2 AP2 PD2 PE 2 AE 2 PF 2 DF 2 82 52 39, AD 39 ;6 20:07:51;用户: 15365143975;邮箱:15365143975;学号: 51233
{#{QQABIYQWU0o4goAQgAgJITAAACABB5gKCFEwwGG6aCCkkEQQsIkEBiLCUCgCEQQgRGCABBqAAEQoDAQABJNgANBIAAB=A}#A}=}#}
同课章节目录
