3.2 平行线分线段成比例 课件(共16张PPT)
文档属性
| 名称 | 3.2 平行线分线段成比例 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 456.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
3.2 平行线分线段成比例
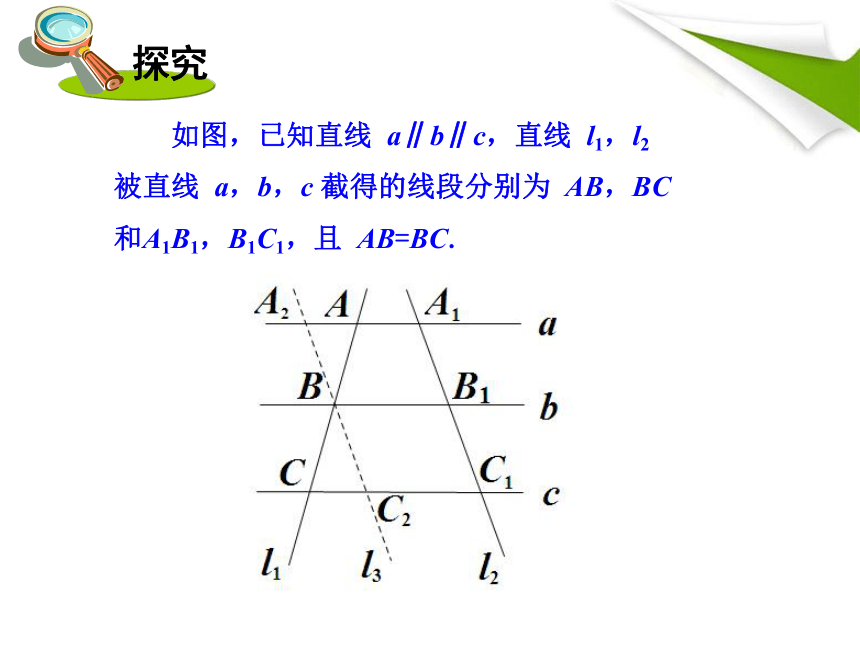
如图,已知直线 a∥b∥c,直线 l1,l2 被直线 a,b,c 截得的线段分别为 AB,BC 和A1B1,B1C1,且 AB=BC.
探究
所以 A1B1=B1C1.
过点 B 作直线 l3∥l2,分别与直线 a,c 相交于点 A2,C2.由于a∥b∥c,l3∥l2,因此由“夹在两平行线间的平行线段相等”可知,
A2B=A1B1,BC2=B1C1.
在△BAA2和△BCC2中,
∠ABA2=∠CBC2,BA=BC,∠BAA2=∠BCC2,
因此 △BAA2≌△BCC2.
从而 BA2=BC2,
结论
由此可以得出:两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
动脑筋
如图,任意两条直线 l1,l2 ,再画三条与 l1,l2 相交的直线 a,b,c .分别度量 l1,l2 被直线 a,b,c 截得的线段 AB,BC ,A1B1,B1C1 的长度. 与 相等吗?
任意平移直线 c,再度量 AB,BC ,A1B1,B1C1 的长度, 与 还相等吗?
结 论
结论
由此得到以下基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
动脑筋
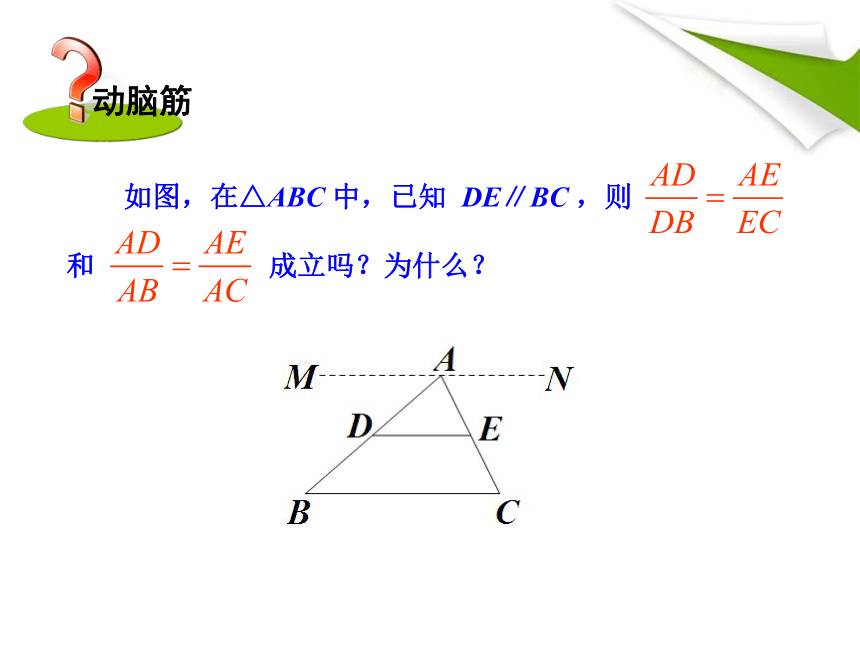
如图,在△ABC 中,已知 DE∥BC ,则 和 成立吗?为什么?
如上图,过点 A 作直线 MN,使 MN∥DE ,
∵DE∥BC ,∴MN∥DE∥BC.
同时还可以得到
因此 AB,AC 被一组平行线 MN,DE,BC 所截,则由平行线分线段成比例可知,
结论
由此得到以下结论:平行于三角形一边的直线截其他两边,所得的对应线段成比例.
例 题
如图,已知 AA1∥BB1∥CC1 ,AB=2,BC=3,A1B1=1.5,求 B1C1 的长.
解 由平行线分线段成比例可知,
练一练
A
练一练
A
练一练
3.2 平行线分线段成比例
如图,已知直线 a∥b∥c,直线 l1,l2 被直线 a,b,c 截得的线段分别为 AB,BC 和A1B1,B1C1,且 AB=BC.
探究
所以 A1B1=B1C1.
过点 B 作直线 l3∥l2,分别与直线 a,c 相交于点 A2,C2.由于a∥b∥c,l3∥l2,因此由“夹在两平行线间的平行线段相等”可知,
A2B=A1B1,BC2=B1C1.
在△BAA2和△BCC2中,
∠ABA2=∠CBC2,BA=BC,∠BAA2=∠BCC2,
因此 △BAA2≌△BCC2.
从而 BA2=BC2,
结论
由此可以得出:两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
动脑筋
如图,任意两条直线 l1,l2 ,再画三条与 l1,l2 相交的直线 a,b,c .分别度量 l1,l2 被直线 a,b,c 截得的线段 AB,BC ,A1B1,B1C1 的长度. 与 相等吗?
任意平移直线 c,再度量 AB,BC ,A1B1,B1C1 的长度, 与 还相等吗?
结 论
结论
由此得到以下基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
动脑筋
如图,在△ABC 中,已知 DE∥BC ,则 和 成立吗?为什么?
如上图,过点 A 作直线 MN,使 MN∥DE ,
∵DE∥BC ,∴MN∥DE∥BC.
同时还可以得到
因此 AB,AC 被一组平行线 MN,DE,BC 所截,则由平行线分线段成比例可知,
结论
由此得到以下结论:平行于三角形一边的直线截其他两边,所得的对应线段成比例.
例 题
如图,已知 AA1∥BB1∥CC1 ,AB=2,BC=3,A1B1=1.5,求 B1C1 的长.
解 由平行线分线段成比例可知,
练一练
A
练一练
A
练一练
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
