3.3 相似的图形 课件(共16张PPT)
文档属性
| 名称 | 3.3 相似的图形 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 18:39:39 | ||
图片预览






文档简介
(共17张PPT)
3.3 相似的图形
问题:
观察下面的图片,它是由其中的一幅图缩小得到的,把一个图形缩小得到的图形与原图形之间有什么关系呢?
问题:
观察下面的图片,它是由其中的一幅图放大得到的,把一个图形放大得到的图形与原图形之间有什么关系呢?
直观上,把一个图形放大(或缩小)得到的图形与原图形是相似的.
因此,以上两组图形分别是相似的.
相同点: 形状相同
不同点: 大小不一定相同
在两个大小不相等的相似图形中,我们可以认为大的图形是由小的图形放大而成,或小的图形是由大的图形缩小而成.
动脑筋
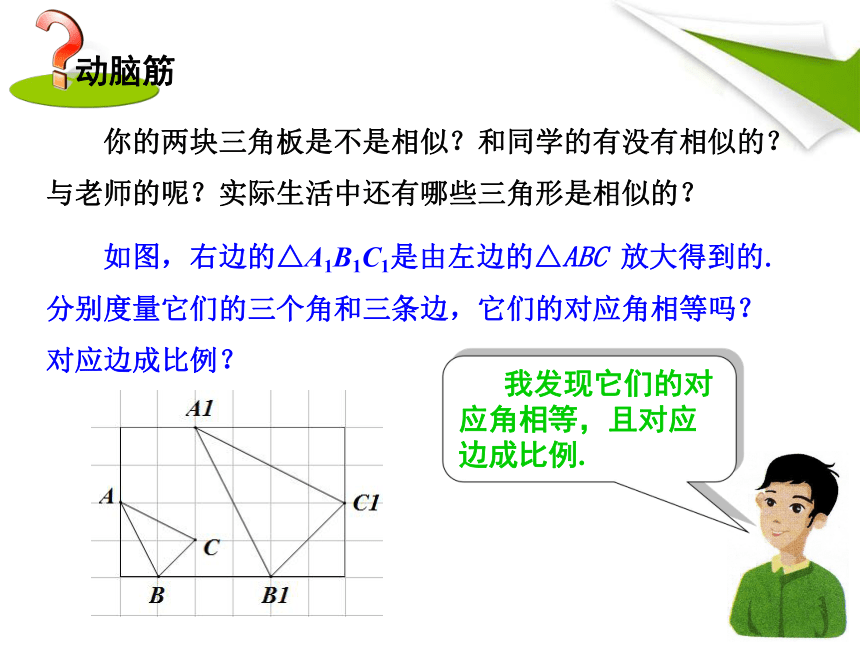
你的两块三角板是不是相似?和同学的有没有相似的?与老师的呢?实际生活中还有哪些三角形是相似的?
我发现它们的对应角相等,且对应边成比例.
如图,右边的△A1B1C1是由左边的△ABC 放大得到的.分别度量它们的三个角和三条边,它们的对应角相等吗?对应边成比例?
结论
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
如果△ABC 与△A1B1C1相似,且点A1,B1,C1分别与点 A,B,C 对应,
则记作:△ABC ∽△A1B1C1,
读作:△ABC 相似于△A1B1C1.
相似三角形的对应边的比叫作相似比.
一般地,若△ABC 与△A1B1C1的相似比为k,则△A1B1C1与△ABC 的相似比为 .
特别地,如果相似比k=1,则△ABC ≌△A1B1C1.因此,三角形全等是三角形相似的特例.
对于相似三角形,有:相似三角形的对应角相等,对应边成比例.
例 题
如图,已知△ABC ∽△A1B1C1,且∠A=48°,AB=8,A1B1=4,AC=6,求∠A1的大小和A1C1的长.
解 ∵△ABC ∽△A1B1C1,
∴∠A=∠A1,
又∵∠A=48°,AB=8,A1B1=4,AC=6,
∴∠A1=48°, ,即A1C1=3.
类似地,对于两个边数相同的多边形,如果它们的对应角相等、对应边成比例,那么这两个多边形叫作相似多边形.
相似多边形的对应边的比叫作相似比.
对于相似多边形,有:相似多边形的对应角相等,对应边成比例.
结论
练一练
1.下列哪两个图形是相似图形( )
A.(1)与(2) B.(1)与(3)
C.(2)与(3) D.(3)与(4)
B
(1)
(2)
(3)
(4)
练一练
2.观察下列图形,指出哪些是相似图形:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
相似图形有:____________________________.
(1)和(8);(2)和(6);(3)和(7)
练一练
3.下列说法正确的有( )
(1)所有的圆都是形状相同的图形;
(2)所有的正方形都是形状相同的图形;
(3)所有的等腰三角形都是形状相同的图形;
(4)所有的矩形都是形状相同的图形;
A.1个 B.2个 C.3个 D.4个
B
4.下列说法中正确的是( ) A.所有平行四边形都是相似图形 B.所有菱形都是相似图形
C.所有等腰梯形都是相似图形 D.所有全等三角形都是相似图形
D
练一练
练一练
5.已知△ADE ∽△ABC,点 A,D,E 分别与点 A,B,C 对应,且相似比为 .若DE=4 cm,求 BC 的长.
3.3 相似的图形
问题:
观察下面的图片,它是由其中的一幅图缩小得到的,把一个图形缩小得到的图形与原图形之间有什么关系呢?
问题:
观察下面的图片,它是由其中的一幅图放大得到的,把一个图形放大得到的图形与原图形之间有什么关系呢?
直观上,把一个图形放大(或缩小)得到的图形与原图形是相似的.
因此,以上两组图形分别是相似的.
相同点: 形状相同
不同点: 大小不一定相同
在两个大小不相等的相似图形中,我们可以认为大的图形是由小的图形放大而成,或小的图形是由大的图形缩小而成.
动脑筋
你的两块三角板是不是相似?和同学的有没有相似的?与老师的呢?实际生活中还有哪些三角形是相似的?
我发现它们的对应角相等,且对应边成比例.
如图,右边的△A1B1C1是由左边的△ABC 放大得到的.分别度量它们的三个角和三条边,它们的对应角相等吗?对应边成比例?
结论
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
如果△ABC 与△A1B1C1相似,且点A1,B1,C1分别与点 A,B,C 对应,
则记作:△ABC ∽△A1B1C1,
读作:△ABC 相似于△A1B1C1.
相似三角形的对应边的比叫作相似比.
一般地,若△ABC 与△A1B1C1的相似比为k,则△A1B1C1与△ABC 的相似比为 .
特别地,如果相似比k=1,则△ABC ≌△A1B1C1.因此,三角形全等是三角形相似的特例.
对于相似三角形,有:相似三角形的对应角相等,对应边成比例.
例 题
如图,已知△ABC ∽△A1B1C1,且∠A=48°,AB=8,A1B1=4,AC=6,求∠A1的大小和A1C1的长.
解 ∵△ABC ∽△A1B1C1,
∴∠A=∠A1,
又∵∠A=48°,AB=8,A1B1=4,AC=6,
∴∠A1=48°, ,即A1C1=3.
类似地,对于两个边数相同的多边形,如果它们的对应角相等、对应边成比例,那么这两个多边形叫作相似多边形.
相似多边形的对应边的比叫作相似比.
对于相似多边形,有:相似多边形的对应角相等,对应边成比例.
结论
练一练
1.下列哪两个图形是相似图形( )
A.(1)与(2) B.(1)与(3)
C.(2)与(3) D.(3)与(4)
B
(1)
(2)
(3)
(4)
练一练
2.观察下列图形,指出哪些是相似图形:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
相似图形有:____________________________.
(1)和(8);(2)和(6);(3)和(7)
练一练
3.下列说法正确的有( )
(1)所有的圆都是形状相同的图形;
(2)所有的正方形都是形状相同的图形;
(3)所有的等腰三角形都是形状相同的图形;
(4)所有的矩形都是形状相同的图形;
A.1个 B.2个 C.3个 D.4个
B
4.下列说法中正确的是( ) A.所有平行四边形都是相似图形 B.所有菱形都是相似图形
C.所有等腰梯形都是相似图形 D.所有全等三角形都是相似图形
D
练一练
练一练
5.已知△ADE ∽△ABC,点 A,D,E 分别与点 A,B,C 对应,且相似比为 .若DE=4 cm,求 BC 的长.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
