第二单元位置(单元自测)(含答案)-2024-2025学年五年级数学上册人教版
文档属性
| 名称 | 第二单元位置(单元自测)(含答案)-2024-2025学年五年级数学上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 875.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 07:47:37 | ||
图片预览



文档简介
第二单元位置(单元自测)-2024-2025学年五年级数学上册人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,若将三角形ABC向左平移3格后的图形是三角形,则顶点的位置用数对表示为( )。
A.(0,4) B.(3,4) C.(2,1)
2.如图,蓝蓝家的位置是(1,1),学校的位置是(3,4)。如果每个小方格的边长表示100米。蓝蓝从家出发,沿着格线行走,经过学校到图书馆,至少要走( )米。
A.500 B.600 C.700 D.800
3.小张坐在教室的第2列第5行,用数对(2,5)表示。如果用数对(x,3)表示小华在教室里的位置,那么下列说法错误的是( )。
A.小华的位置一定在第3列 B.小华的位置一定在第3行
C.小华的位置可能在第3列 D.小华的位置不能确定
4.小丽坐在第4列,第3行,用(4,3)表示。小明坐在第5列,第1行,表示为( )。
A.(1,5) B.(5,1) C.(2,5)
5.如图,如果将三角形ABC向右平移3格,再向上平移2格,得到的新三角形的顶点A对应的位置可以用数对( )表示。
A.(1,1) B.(4,2) C.(4,3)
6.如图,如果点A的位置表示为(3,4),点B的位置表示为(5,2),则下列选项( )表示的位置不在方格图中。
A.(1,3) B.(3,1) C.(6,1) D.(2,2)
二、填空题
7.李浩买了一张电影票,座位号是4排5座,用数对表示为(5,4)。张红买了同一场的电影票,她的座位用数对表示为(8,2),那么张红的座位是( )排( )座。
8.小明和小亮坐在同一列,小明和小东坐在同一行,已知小亮的位置是(5,3),小东的位置是(3,5),那么小明的位置是( , )
9.报告厅里,小芳坐在第10列第8行,可以表示为(10,8),小明坐在第6列第12行,可以表示为( ),小东的位置是(3,2)表示他坐在第( )列第( )行.
10.如图,若A点的位置是(3,2),则B点的位置为( ),C点的位置是( )。
11.李静坐在教室的第6列第3行,用数对(6,3)表示。小军坐在第7列第5行,用数对( )表示。
12.如图,A点用数对表示为( ),B点用数对表示为( ),C点用数对表示为( )。
13.小红在教室里的位置用数对表示是(5,2),表示坐在第5列、第2行的位置;小花在教室里的位置用数对表示是(3,5),表示坐在第( )列、第( )行的位置。
14.聪聪和小刚坐在同一列,和小明坐在同一行。已知小刚的位置是(3,2),小明的位置是(1,5),那么聪聪的位置用数对表示是( )。
15.数字不仅可以用来表示数量和顺序,还可以用来表示( ),第4列第6行用数对表示为(4,6),则(6,5)表示第( )列第( )行。
16.王东在班上的座位用数对表示是(5,6),他坐在第( )列第( )行,张力与他同桌,张力的座位用数对表示可能是( ),也可能是( )。
17.在一节电脑课上,小强的位置是(8,6),表示他坐在第( )列,第( )行,小明的座位是第4列,第6行,用数对( , )表示,他们俩之间隔了( )个人。
三、判断题
18.小刚的位置是(3,5),小芳的位置是(4,5),他们是同桌。( )
19.小刚的座位在第2行第3列,则记为(2,3). ( )
20.在同一幅图上,点和点在同一行。( )
21.虽不知道(2,)表示的位置是第几列,但知道是第2行。( )
22.如果一个点用数对表示是(2,6),先向左平移2格,再向上平移3格,现在的位置在(1,9). ( )
23.小军坐在观众席的第2列第3行,用数对(2,3)表示,小美坐在小军正后方的第二个位置,用数对表示是(4,3)。( )
四、计算题
24.直接写得数.
0.65×4= 1.24×0.2= 2.4×2.5= 1.3×20=
0.01×7.2= 1.82×0= 0.8×1.25= 60×0.5=
25.列竖式计算并按要求保留积的位数。
8.4×1.8= 32×1.5= 4.28×0.32≈ (保留两位小数)
26.能简算的要简算
4.2×1.5-2.74 5.9×4.8+5.9×5.2 1.25×8.8
0.25×2.6×4 15.8×101-15.8 8×(20-1.25)
五、作图题
27.在下图中标出点A(3,4),B(10,6),C(13,3),D(6,1),再依次连成封闭图形。
六、解答题
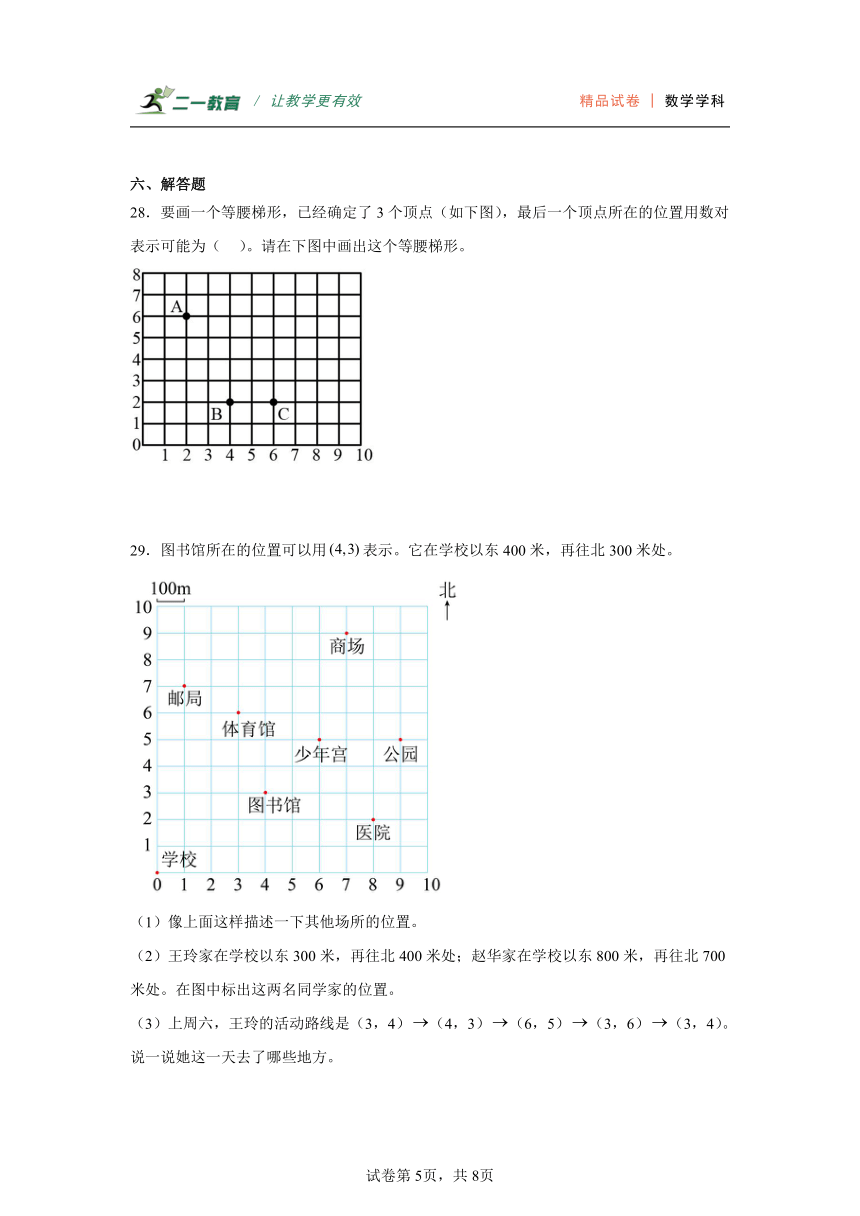
28.要画一个等腰梯形,已经确定了3个顶点(如下图),最后一个顶点所在的位置用数对表示可能为( )。请在下图中画出这个等腰梯形。
29.图书馆所在的位置可以用表示。它在学校以东400米,再往北300米处。
(1)像上面这样描述一下其他场所的位置。
(2)王玲家在学校以东300米,再往北400米处;赵华家在学校以东800米,再往北700米处。在图中标出这两名同学家的位置。
(3)上周六,王玲的活动路线是(3,4)(4,3)(6,5)(3,6)(3,4)。说一说她这一天去了哪些地方。
30.看图画一画,再用数对表示各点的位置。
(1)如果A点的位置为(1,6),请你写出B、C点的位置。B( ),C( )。
(2)画出三角形向下平移3个单位的图形,并写出顶点A′、B′、C′的位置。
(3)画出三角形向右平移5个单位的图形,并写出顶点A″、B″、C″的位置。
31.(1)写出三角形各个顶点的位置。
(2)画出三角形先向左平移5格,再向下平移3格后的图形,并写出其各个顶点的位置。
32.(1)把图中的三角形向右平移3格,得到三角形。
(2)用数对表示两个三角形顶点的位置。
( ) ( ) ( )
( ) ( ) ( )
33.看图解决问题。
图中每个小正方形的边长是50米。
(1)图中点用数对表示是( )。
(2)以图中虚线为对称轴,画出三角形的轴对称图形。
(3)画出三角形向右平移10格的图形。
(4)从点出发,向北方走,如果每分钟走50米,3分钟刚好到小刚家。请你在图上标出小刚家的位置,并用字母表示。
34.观察下图,回答问题。
(1)你能像小明那样描述图书馆和少年宫的位置吗?
(2)小明家在小军家以西,再往北处。在图中标出小明家的位置。
(3)周末,小军的活动路线是:
(6,1)→(4,3)→(5,5)→(3,7)→(2,5)→(6,1)。说说他这一天先后去了哪些地方。
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】将三角形ABC的各点向左平移3格后,再顺次连接各点即可得到三角形;再根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此用数对表示出顶点的位置。
【详解】如图所示:
顶点的位置用数对表示为(3,4)。
故答案为:B
2.D
【分析】根据蓝蓝甲和学校位置的数对,结合图形得出蓝蓝从家出发去到学校需要经过5条正方形的边,再从学校去到图书馆需要经过3条正方形的边。每条边长100米,计算即可。
【详解】5×100=500(米)
3×100=300(米)
500+300=800(米)
故答案为:D
【点睛】此题考查了用数对表示位置的方法,明确数对的含义是关键。
3.A
【分析】用数对表示位置时,前一个数表示第几列,后一个数表示第几行;(x,3)表示在第x列第3行,据此解答。
【详解】根据分析可知,如果用数对(x,3)表示小华在教室里的位置,那么小华的位置一定在第3行,可能在第3列,也可能在其他列,位置不确定。
故答案为:A
4.B
【解析】根据题意可得数对的第一个数字表示列,第二个数字表示行,即可得出答案。
【详解】小丽坐在第4列,第3行,用(4,3)表示。小明坐在第5列,第1行,表示为 (5,1)。
故答案为:B。
【点睛】关键是理解数对的意义,明确数对中的两个数分别表示的是什么。
5.C
【分析】先将三角形进行平移,再确定位置,数对中第一个数字表示列,第二个数字表示行,由此解答即可。
【详解】如图:
得到的新三角形的顶点A对应的位置可以用数对(4,3)表示。
故答案为:C
6.C
【分析】根据数对表示位置的方法:第一个数字表示列,第二个数字表示行;据此分析各选项的点在不在方格中。
【详解】A.如图:(1,3)在方格中;
B.如图:(3,1)在方格中;
C.(6,1)不在方格中;
D.如图:(2,2)在方格中。
如图:
如果点A的位置表示为(3,4),点B的位置表示为(5,2),则下列选项(6,1)表示的位置不在方格图中。
故答案为:C
7. 2 8
【分析】根据座位号是4排5座,用数对表示为(5,4)可知,数对的第一个数表示座,第二个数表示排,据此确定张红的排数和座数即可。
【详解】张红买了同一场的电影票,她的座位用数对表示为(8,2),那么张红的座位是2排8座。
【点睛】用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
8. 5 5
【分析】数对中第一个数字表示列,第二个数字表示行;小明和小亮坐在同一列,说明小明在第5列;小明和小东坐在同一行,说明小明在第5行,据此解答即可。
【详解】小明的位置是(5,5)
【点睛】明确数对表示位置时的特点是解答本题的关键。
9. (6,12) 3 2
【详解】数对里第一个数表示列,第二个数表示行.据此作答即可.
10. (3,3) (6,4)
【分析】根据数对的意义,用数对表示位置,第一个数表示所在的列数,第二个数表示所在的行数。
【详解】B点的上位置为(3,3);C点的位置是(6,4)
11.(7,5)
【分析】用数对表示位置,第一个数表示列,第二个数表示行,据此解答即可。
【详解】小军坐在第7列第5行,用数对(7,5)表示。
【点睛】本题考查用数对表示位置,解答本题的关键是掌握用数对表示位置的方法。
12. (1,l) (5,1) (3,3)
【分析】数对的表示方法:(列数,行数),根据图形找到各点对应的列数和行数即可。
【详解】A点用数对表示为( 1,l ),B点用数对表示为( 5,1 ),C点用数对表示为( 3,3 )。
【点睛】掌握数对的表示方法是解答题目的关键。
13. 3 5
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,据此解答。
【详解】(5,2)表示坐在第5列,第2行的位置;
(3,5)表示坐在第3列,第5行的位置。
小红在教室里的位置用数对表示是(5,2),表示坐在第5列、第2行的位置;小花在教室里的位置用数对表示是(3,5),表示坐在第3列,第5行的位置。
【点睛】熟练掌握数对表示位置的方法是解答本题的关键。
14.(3,5)
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,小刚的位置是(3,2),则小刚是第3列第2行;小明的位置(1,5),则小明是第1列第5行;由此得出聪聪的位置是第3列第5行,据此用数对表示即可。
【详解】由分析可得,聪聪的位置是第3列第5行,用数对表示为(3,5)。
【点睛】本题考查了数对表示位置的方法。明确第一个数字表示列,第二个数字表示行是关键。
15. 编码 6 5
【分析】数字不仅可以用来表示数量和顺序,还可以用来表示编码,在日常生活中,我们可以接触到很多数字组成的编码,像邮政编码、门牌号、车牌号等;(答案不唯一,比如数字还可以用来表示位置。)
在用数对表述物体位置时,括号里的第一个数字表示物体所在的列,第二个数字表示物体所在的行,根据这一原则答题即可。
【详解】由分析可得:
数字不仅可以用来表示数量和顺序,还可以用来表示编码(答案不唯一),第4列第6行用数对表示为(4,6),则(6,5)表示第6列第5行。
【点睛】本题主要考查了用数对表示位置以及根据位置来写出数对,一定要仔细观察,知道数对括号里的第一个数表示物体所在的列,第二个数字表示物体所在的行。
16. 5 6 (4,6) (6,6)
【分析】平面内,从左往右数是列数,从前往后数是行数,表示物体的位置时,以(列数,行数)的形式呈现,就是数对;
一个数对,前面的数字表示列数,后面的数字表示行数,王东的座位用数对表示是(5,6),则他坐在第5列、第6行;
平面内,位于竖直方向同一条直线上的数对,列数相同,位于水平方向同一条直线上的数对,行数相同,因为张力与王东同桌,即在同一条水平线上,张力可能在王东的左面,位置就是(4,6),或者在王东的右面,位置就是(6,6)。
【详解】结合用数对表示位置的方法以及根据数对确定位置的方法可得:
王东在班上的座位用数对表示是(5,6),他坐在第(5)列第(6)行,张力与他同桌,张力的座位用数对表示可能是(4,6),也可能是(6,6)。
【点睛】先仔细审题,结合数对的意义,确定王东位置所在列数和行数;再发挥空间想象,合理猜测张力的位置。
17. 8 6 4 6 3
【分析】根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行;竖排叫做列,横排叫做行;确定第几列一般从左往右数;
确定第几排一般从下往上数,根据物体所在行与列可用对数表示出物体的位置;据此解答。
【详解】在一节电脑课上,小强的位置是(8,6)表示他坐在底8列,第6行,小明的座位是第4列,第6行,用对数(4,6)表示,他们之间隔了3人。
【点睛】本题考查用数对表示物体位置的方法,关键是看准物体所在的列与行。
18.√
【分析】本题主要考查的是用数对表示位置,要记得在数对中左边的数字表示第几列,右边的数字表示第几行。
【详解】根据数对的含义,小刚的位置是(3,5),表示的是第3列,第5行;小芳的位置在(4,5),表示的是第4列,第5行。因为小刚和小芳在同一行,紧挨着的两列,根据位置空间分布,两个人是同桌。
所以判断正确。
19.×
【详解】略
20.×
【分析】数对的第一个数表示列,第二个数表示行,据此分析。
【详解】在第三列第七行,在第三列第九行,两个点在同一列,所以原题说法错误。
【点睛】关键是掌握数对表示位置的方法。
21.×
【分析】用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此判断。
【详解】虽不知道(2,)表示的位置是第几行,但知道是第2列。
原题说法错误。
故答案为:×
22.×
【分析】数对中,向上平移多少就把逗号后面的数加多少,向下平移多少就把逗号后面的数减多少,向左平移多少就把逗号前面的数减多少,向右平移多少就把逗号前面的数加多少.
【详解】数对(2,6)向左平移2格后,位置在(0,6),再向上平移3格,现在的位置在(0,9).故答案为错误.
23.×
【分析】由题意可知:数对的第一个数表示列,第二个数表示行,小军坐在观众席的第2列第3行,小美坐在小军正后方的第二个位置,列数不变,行数增加2,据此解答。
【详解】根据分析得,3+2=5(行)
小美与小军坐在同一列,在第2列第5行,用数对表示是(2,5)。
故答案为:×
【点睛】本题考查用数对表示位置,解答本题的关键是掌握数对的概念。
24.2.6;0.248;6;26
0.072;0;1;30
【详解】小数乘法法则:①按照整数乘法法则先求出积。②看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
【点睛】小数乘法口算,注意最后小数点的位置。
25.15.12;48;1.37
【分析】小数乘法法则:(1)按整数乘法的法则先求出积;(2)看因数中一个有几位小数,就从积的右边起数出几位点上小数点。
根据四舍五入法保留近似数。
【详解】8.4×1.8=15.12 32×1.5=48 4.28×0.32≈1.37
26.3.56;59;11
2.6;1580;150
【分析】4.2×1.5-2.74,根据四则混合运算的顺序计算即可;
5.9×4.8+5.9×5.2,用乘法分配律进行简算;
1.25×8.8,用乘法分配律或结合律均可进行简算;
0.25×2.6×4,用乘法交换律进行简算;
15.8×101-15.8,用乘法分配律进行简算;
8×(20-1.25),用乘法分配律进行简算。
【详解】4.2×1.5-2.74
=6.3-2.74
=3.56
5.9×4.8+5.9×5.2
=(4.8+5.2)×5.9
=10×5.9
=59
1.25×8.8
=1.25×8×1.1
=10×1.1
=11
0.25×2.6×4
=0.25×4×2.6
=1×2.6
=2.6
15.8×101-15.8
=15.8×(101-1)
=15.8×100
=1580
8×(20-1.25)
=8×20-8×1.25
=160-10
=150
【点睛】本题考查了小数的四则混合运算和简便计算,整数的四则混合运算顺序和运算定律同样适用于小数。
27.见详解
【分析】用数对表示位置时,通常把竖排叫列,横排叫行。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
【详解】作图如下:
【点睛】一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。
28.(8,6);图见详解
【分析】根据用数对表示位置时,先表示第几列,再表示第几行即可解答。
【详解】由分析可得:后一个顶点所在的位置用数对表示可能为(8,6)
作图如下:
【点睛】本题主要考查用数对表示位置和梯形的认识。
29.见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此用数对表示出各个场所的位置,以学校为观测点,再根据“上北下南,左西右东”及距离解答即可;
(2)根据“上北下南,左西右东”及距离标出这两名同学家的位置;
(3)根据用数对表示位置的方法,找出各个场所的位置,进而描述王玲的活动路线即可。
【详解】(1)医院是,它在学校的以东800米,再往北200米处;少年宫是,它在学校的以东600米,再往北500米处;体育馆所在的位置可以用表示。它在学校以东300米,再往北600米处;邮局所在的位置可以用表示。它在学校以东100米,再往北700米处;公园所在的位置可以用表示。它在学校以东900米,再往北500米处;商场所在的位置可以用表示。它在学校以东700米,再往北900米处。
(2)如图:
(3)王玲从家出发到图书馆,再到少年宫,又去了体育馆,最后回到了家中。
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
30.(1)B(2,5),C(3,11)
(2)(3)见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此用数对表示出点B、C的位置即可;
(2)将三角形的各个顶点向下平移3个单位,再顺次连接各点即可;再根据用数对表示位置的方法表示出顶点A′、B′、C′的位置;
(3)将三角形的各个顶点向右平移5个单位,再顺次连接各点即可;再根据用数对表示位置的方法表示出顶点将三角形的各个顶点向下平移3个单位,再顺次连接各点即可;再根据用数对表示位置的方法表示出顶点A″、B″、C″的位置。
【详解】(1)如果A点的位置为(1,6),则B(2,5),C(3,11)。
(2)(3)如图所示:
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
31.(1)B(6,4);C(9,3);(2)A′(3,2);B′(1,1);C′(4,0)
【分析】(1)用数对表示位置时,前一个数表示第几列,后一个数表示第几行;
(2)根据平移的特征,把三角形ABC的各顶点分别先向左平移5格,再向下平移3格,依次连接即可得到平移后的三角形A′B′C′,再用数对表示三个顶点的位置。
【详解】(1)B(6,4),C(9,3);
(2)如图:
A′(3,2);B′(1,1);C′(4,0)。
【点睛】本题考查了图形的平移以及用数对表示位置的方法,平移作图要注意:①方向;②距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动。
32.(1)见详解
(2)(2,1) (3,3) (5,1)
(5,1) (6,3) (8,1)
【分析】(1)根据图形平移的方法,先把图中三角形的三个顶点向右平移3格,再把它们依次连接起来,即可得出平移后的三角形;
(2)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可标出三角形顶点的位置。
【详解】(1)如图如下:
(2)根据数对表示位置的方法,用数对表示三角形顶点分别是:
(2,1) (3,3) (5,1)(5,1) (6,3) (8,1)。
【点睛】此题考查了图形平移的方法以及数对表示位置的方法的灵活应用,掌握数对表示位置的方法是:第一个数字表示列,第二个数字表示行是解题关键。
33.(1)(12,6)
(2)(3)(4)见详解
【分析】(1)数对的括号中,第一个数字表示列,第二个数字表示行,据此解答。
(2)画轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(3)将三角形ABC的各点向右移动平移10格,然后连接即可。
(4)从点出发,向北方走,每分钟走50米,3分钟刚好到小刚家,也就是从D点开始,向上平移50×3=150(米),也就是3格,标注F即可。
【详解】(1)通过观察O点的位置,可知,是第12列,第6行,用数对表示(12,6)。
(2)(3)(4)如下图:
【点睛】此题主要考查学生对数对、物体平移和轴对称图形的认识与应用。
34.(1)图书馆的位置用数对(4,3)表示,在小军家以西200米,以北200米处;
少年宫的位置为(3,7),在小军家以西300米,以北600米处;
(2)见详解;
(3)小军家→图书馆→博物馆→少年宫→邮局→小军家
【分析】(1)根据例句,数对中第一个数表示列数,第二个数表示行数,先找到图书馆的位置用数对表示,再看在小军家以西2格,再往北2格,这里1格代表100米,算出实际距离为2×100=200米;同理描述少年宫。
(2)以小军家为观测点,根据“上北下南,左西右东”,判断方向,再根据1格代表100米,500米和300米分别代表几个100米就是几格,找到小明家位置。
(3)根据数对找出点所对应的地方,按顺序描述路线。
【详解】(1)图书馆位置(4,3)
在小军家以西:2×100=200(米)再往北:2×100=200(米);
少年宫位置(3,7)
在小军家以西:3×100=300(米)
再往北:6×100=600(米)
答:图书馆所在位置可以用(4,3)表示,它在小军家以西200米,再往北200米处;
少年宫所在位置可以用(3,7)表示,它在小军家以西300米,再往北600米处。
(2)500里面包含5个100;300里面有3个100。再根据“上北下南,左西右东”绘图找点。
(3)根据数对中第一个数表示列数,第二个数表示行数,知道(6,1)代表小军家,(4,3)表示图书馆;(5,5)表示博物馆;(3,7)代表少年宫;(2,5)代表邮局;(6,1)代表小军家。
故周末,小军的活动路线是:小军家→图书馆→博物馆→少年宫→邮局→小军家。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,若将三角形ABC向左平移3格后的图形是三角形,则顶点的位置用数对表示为( )。
A.(0,4) B.(3,4) C.(2,1)
2.如图,蓝蓝家的位置是(1,1),学校的位置是(3,4)。如果每个小方格的边长表示100米。蓝蓝从家出发,沿着格线行走,经过学校到图书馆,至少要走( )米。
A.500 B.600 C.700 D.800
3.小张坐在教室的第2列第5行,用数对(2,5)表示。如果用数对(x,3)表示小华在教室里的位置,那么下列说法错误的是( )。
A.小华的位置一定在第3列 B.小华的位置一定在第3行
C.小华的位置可能在第3列 D.小华的位置不能确定
4.小丽坐在第4列,第3行,用(4,3)表示。小明坐在第5列,第1行,表示为( )。
A.(1,5) B.(5,1) C.(2,5)
5.如图,如果将三角形ABC向右平移3格,再向上平移2格,得到的新三角形的顶点A对应的位置可以用数对( )表示。
A.(1,1) B.(4,2) C.(4,3)
6.如图,如果点A的位置表示为(3,4),点B的位置表示为(5,2),则下列选项( )表示的位置不在方格图中。
A.(1,3) B.(3,1) C.(6,1) D.(2,2)
二、填空题
7.李浩买了一张电影票,座位号是4排5座,用数对表示为(5,4)。张红买了同一场的电影票,她的座位用数对表示为(8,2),那么张红的座位是( )排( )座。
8.小明和小亮坐在同一列,小明和小东坐在同一行,已知小亮的位置是(5,3),小东的位置是(3,5),那么小明的位置是( , )
9.报告厅里,小芳坐在第10列第8行,可以表示为(10,8),小明坐在第6列第12行,可以表示为( ),小东的位置是(3,2)表示他坐在第( )列第( )行.
10.如图,若A点的位置是(3,2),则B点的位置为( ),C点的位置是( )。
11.李静坐在教室的第6列第3行,用数对(6,3)表示。小军坐在第7列第5行,用数对( )表示。
12.如图,A点用数对表示为( ),B点用数对表示为( ),C点用数对表示为( )。
13.小红在教室里的位置用数对表示是(5,2),表示坐在第5列、第2行的位置;小花在教室里的位置用数对表示是(3,5),表示坐在第( )列、第( )行的位置。
14.聪聪和小刚坐在同一列,和小明坐在同一行。已知小刚的位置是(3,2),小明的位置是(1,5),那么聪聪的位置用数对表示是( )。
15.数字不仅可以用来表示数量和顺序,还可以用来表示( ),第4列第6行用数对表示为(4,6),则(6,5)表示第( )列第( )行。
16.王东在班上的座位用数对表示是(5,6),他坐在第( )列第( )行,张力与他同桌,张力的座位用数对表示可能是( ),也可能是( )。
17.在一节电脑课上,小强的位置是(8,6),表示他坐在第( )列,第( )行,小明的座位是第4列,第6行,用数对( , )表示,他们俩之间隔了( )个人。
三、判断题
18.小刚的位置是(3,5),小芳的位置是(4,5),他们是同桌。( )
19.小刚的座位在第2行第3列,则记为(2,3). ( )
20.在同一幅图上,点和点在同一行。( )
21.虽不知道(2,)表示的位置是第几列,但知道是第2行。( )
22.如果一个点用数对表示是(2,6),先向左平移2格,再向上平移3格,现在的位置在(1,9). ( )
23.小军坐在观众席的第2列第3行,用数对(2,3)表示,小美坐在小军正后方的第二个位置,用数对表示是(4,3)。( )
四、计算题
24.直接写得数.
0.65×4= 1.24×0.2= 2.4×2.5= 1.3×20=
0.01×7.2= 1.82×0= 0.8×1.25= 60×0.5=
25.列竖式计算并按要求保留积的位数。
8.4×1.8= 32×1.5= 4.28×0.32≈ (保留两位小数)
26.能简算的要简算
4.2×1.5-2.74 5.9×4.8+5.9×5.2 1.25×8.8
0.25×2.6×4 15.8×101-15.8 8×(20-1.25)
五、作图题
27.在下图中标出点A(3,4),B(10,6),C(13,3),D(6,1),再依次连成封闭图形。
六、解答题
28.要画一个等腰梯形,已经确定了3个顶点(如下图),最后一个顶点所在的位置用数对表示可能为( )。请在下图中画出这个等腰梯形。
29.图书馆所在的位置可以用表示。它在学校以东400米,再往北300米处。
(1)像上面这样描述一下其他场所的位置。
(2)王玲家在学校以东300米,再往北400米处;赵华家在学校以东800米,再往北700米处。在图中标出这两名同学家的位置。
(3)上周六,王玲的活动路线是(3,4)(4,3)(6,5)(3,6)(3,4)。说一说她这一天去了哪些地方。
30.看图画一画,再用数对表示各点的位置。
(1)如果A点的位置为(1,6),请你写出B、C点的位置。B( ),C( )。
(2)画出三角形向下平移3个单位的图形,并写出顶点A′、B′、C′的位置。
(3)画出三角形向右平移5个单位的图形,并写出顶点A″、B″、C″的位置。
31.(1)写出三角形各个顶点的位置。
(2)画出三角形先向左平移5格,再向下平移3格后的图形,并写出其各个顶点的位置。
32.(1)把图中的三角形向右平移3格,得到三角形。
(2)用数对表示两个三角形顶点的位置。
( ) ( ) ( )
( ) ( ) ( )
33.看图解决问题。
图中每个小正方形的边长是50米。
(1)图中点用数对表示是( )。
(2)以图中虚线为对称轴,画出三角形的轴对称图形。
(3)画出三角形向右平移10格的图形。
(4)从点出发,向北方走,如果每分钟走50米,3分钟刚好到小刚家。请你在图上标出小刚家的位置,并用字母表示。
34.观察下图,回答问题。
(1)你能像小明那样描述图书馆和少年宫的位置吗?
(2)小明家在小军家以西,再往北处。在图中标出小明家的位置。
(3)周末,小军的活动路线是:
(6,1)→(4,3)→(5,5)→(3,7)→(2,5)→(6,1)。说说他这一天先后去了哪些地方。
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】将三角形ABC的各点向左平移3格后,再顺次连接各点即可得到三角形;再根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此用数对表示出顶点的位置。
【详解】如图所示:
顶点的位置用数对表示为(3,4)。
故答案为:B
2.D
【分析】根据蓝蓝甲和学校位置的数对,结合图形得出蓝蓝从家出发去到学校需要经过5条正方形的边,再从学校去到图书馆需要经过3条正方形的边。每条边长100米,计算即可。
【详解】5×100=500(米)
3×100=300(米)
500+300=800(米)
故答案为:D
【点睛】此题考查了用数对表示位置的方法,明确数对的含义是关键。
3.A
【分析】用数对表示位置时,前一个数表示第几列,后一个数表示第几行;(x,3)表示在第x列第3行,据此解答。
【详解】根据分析可知,如果用数对(x,3)表示小华在教室里的位置,那么小华的位置一定在第3行,可能在第3列,也可能在其他列,位置不确定。
故答案为:A
4.B
【解析】根据题意可得数对的第一个数字表示列,第二个数字表示行,即可得出答案。
【详解】小丽坐在第4列,第3行,用(4,3)表示。小明坐在第5列,第1行,表示为 (5,1)。
故答案为:B。
【点睛】关键是理解数对的意义,明确数对中的两个数分别表示的是什么。
5.C
【分析】先将三角形进行平移,再确定位置,数对中第一个数字表示列,第二个数字表示行,由此解答即可。
【详解】如图:
得到的新三角形的顶点A对应的位置可以用数对(4,3)表示。
故答案为:C
6.C
【分析】根据数对表示位置的方法:第一个数字表示列,第二个数字表示行;据此分析各选项的点在不在方格中。
【详解】A.如图:(1,3)在方格中;
B.如图:(3,1)在方格中;
C.(6,1)不在方格中;
D.如图:(2,2)在方格中。
如图:
如果点A的位置表示为(3,4),点B的位置表示为(5,2),则下列选项(6,1)表示的位置不在方格图中。
故答案为:C
7. 2 8
【分析】根据座位号是4排5座,用数对表示为(5,4)可知,数对的第一个数表示座,第二个数表示排,据此确定张红的排数和座数即可。
【详解】张红买了同一场的电影票,她的座位用数对表示为(8,2),那么张红的座位是2排8座。
【点睛】用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
8. 5 5
【分析】数对中第一个数字表示列,第二个数字表示行;小明和小亮坐在同一列,说明小明在第5列;小明和小东坐在同一行,说明小明在第5行,据此解答即可。
【详解】小明的位置是(5,5)
【点睛】明确数对表示位置时的特点是解答本题的关键。
9. (6,12) 3 2
【详解】数对里第一个数表示列,第二个数表示行.据此作答即可.
10. (3,3) (6,4)
【分析】根据数对的意义,用数对表示位置,第一个数表示所在的列数,第二个数表示所在的行数。
【详解】B点的上位置为(3,3);C点的位置是(6,4)
11.(7,5)
【分析】用数对表示位置,第一个数表示列,第二个数表示行,据此解答即可。
【详解】小军坐在第7列第5行,用数对(7,5)表示。
【点睛】本题考查用数对表示位置,解答本题的关键是掌握用数对表示位置的方法。
12. (1,l) (5,1) (3,3)
【分析】数对的表示方法:(列数,行数),根据图形找到各点对应的列数和行数即可。
【详解】A点用数对表示为( 1,l ),B点用数对表示为( 5,1 ),C点用数对表示为( 3,3 )。
【点睛】掌握数对的表示方法是解答题目的关键。
13. 3 5
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,据此解答。
【详解】(5,2)表示坐在第5列,第2行的位置;
(3,5)表示坐在第3列,第5行的位置。
小红在教室里的位置用数对表示是(5,2),表示坐在第5列、第2行的位置;小花在教室里的位置用数对表示是(3,5),表示坐在第3列,第5行的位置。
【点睛】熟练掌握数对表示位置的方法是解答本题的关键。
14.(3,5)
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,小刚的位置是(3,2),则小刚是第3列第2行;小明的位置(1,5),则小明是第1列第5行;由此得出聪聪的位置是第3列第5行,据此用数对表示即可。
【详解】由分析可得,聪聪的位置是第3列第5行,用数对表示为(3,5)。
【点睛】本题考查了数对表示位置的方法。明确第一个数字表示列,第二个数字表示行是关键。
15. 编码 6 5
【分析】数字不仅可以用来表示数量和顺序,还可以用来表示编码,在日常生活中,我们可以接触到很多数字组成的编码,像邮政编码、门牌号、车牌号等;(答案不唯一,比如数字还可以用来表示位置。)
在用数对表述物体位置时,括号里的第一个数字表示物体所在的列,第二个数字表示物体所在的行,根据这一原则答题即可。
【详解】由分析可得:
数字不仅可以用来表示数量和顺序,还可以用来表示编码(答案不唯一),第4列第6行用数对表示为(4,6),则(6,5)表示第6列第5行。
【点睛】本题主要考查了用数对表示位置以及根据位置来写出数对,一定要仔细观察,知道数对括号里的第一个数表示物体所在的列,第二个数字表示物体所在的行。
16. 5 6 (4,6) (6,6)
【分析】平面内,从左往右数是列数,从前往后数是行数,表示物体的位置时,以(列数,行数)的形式呈现,就是数对;
一个数对,前面的数字表示列数,后面的数字表示行数,王东的座位用数对表示是(5,6),则他坐在第5列、第6行;
平面内,位于竖直方向同一条直线上的数对,列数相同,位于水平方向同一条直线上的数对,行数相同,因为张力与王东同桌,即在同一条水平线上,张力可能在王东的左面,位置就是(4,6),或者在王东的右面,位置就是(6,6)。
【详解】结合用数对表示位置的方法以及根据数对确定位置的方法可得:
王东在班上的座位用数对表示是(5,6),他坐在第(5)列第(6)行,张力与他同桌,张力的座位用数对表示可能是(4,6),也可能是(6,6)。
【点睛】先仔细审题,结合数对的意义,确定王东位置所在列数和行数;再发挥空间想象,合理猜测张力的位置。
17. 8 6 4 6 3
【分析】根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行;竖排叫做列,横排叫做行;确定第几列一般从左往右数;
确定第几排一般从下往上数,根据物体所在行与列可用对数表示出物体的位置;据此解答。
【详解】在一节电脑课上,小强的位置是(8,6)表示他坐在底8列,第6行,小明的座位是第4列,第6行,用对数(4,6)表示,他们之间隔了3人。
【点睛】本题考查用数对表示物体位置的方法,关键是看准物体所在的列与行。
18.√
【分析】本题主要考查的是用数对表示位置,要记得在数对中左边的数字表示第几列,右边的数字表示第几行。
【详解】根据数对的含义,小刚的位置是(3,5),表示的是第3列,第5行;小芳的位置在(4,5),表示的是第4列,第5行。因为小刚和小芳在同一行,紧挨着的两列,根据位置空间分布,两个人是同桌。
所以判断正确。
19.×
【详解】略
20.×
【分析】数对的第一个数表示列,第二个数表示行,据此分析。
【详解】在第三列第七行,在第三列第九行,两个点在同一列,所以原题说法错误。
【点睛】关键是掌握数对表示位置的方法。
21.×
【分析】用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此判断。
【详解】虽不知道(2,)表示的位置是第几行,但知道是第2列。
原题说法错误。
故答案为:×
22.×
【分析】数对中,向上平移多少就把逗号后面的数加多少,向下平移多少就把逗号后面的数减多少,向左平移多少就把逗号前面的数减多少,向右平移多少就把逗号前面的数加多少.
【详解】数对(2,6)向左平移2格后,位置在(0,6),再向上平移3格,现在的位置在(0,9).故答案为错误.
23.×
【分析】由题意可知:数对的第一个数表示列,第二个数表示行,小军坐在观众席的第2列第3行,小美坐在小军正后方的第二个位置,列数不变,行数增加2,据此解答。
【详解】根据分析得,3+2=5(行)
小美与小军坐在同一列,在第2列第5行,用数对表示是(2,5)。
故答案为:×
【点睛】本题考查用数对表示位置,解答本题的关键是掌握数对的概念。
24.2.6;0.248;6;26
0.072;0;1;30
【详解】小数乘法法则:①按照整数乘法法则先求出积。②看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
【点睛】小数乘法口算,注意最后小数点的位置。
25.15.12;48;1.37
【分析】小数乘法法则:(1)按整数乘法的法则先求出积;(2)看因数中一个有几位小数,就从积的右边起数出几位点上小数点。
根据四舍五入法保留近似数。
【详解】8.4×1.8=15.12 32×1.5=48 4.28×0.32≈1.37
26.3.56;59;11
2.6;1580;150
【分析】4.2×1.5-2.74,根据四则混合运算的顺序计算即可;
5.9×4.8+5.9×5.2,用乘法分配律进行简算;
1.25×8.8,用乘法分配律或结合律均可进行简算;
0.25×2.6×4,用乘法交换律进行简算;
15.8×101-15.8,用乘法分配律进行简算;
8×(20-1.25),用乘法分配律进行简算。
【详解】4.2×1.5-2.74
=6.3-2.74
=3.56
5.9×4.8+5.9×5.2
=(4.8+5.2)×5.9
=10×5.9
=59
1.25×8.8
=1.25×8×1.1
=10×1.1
=11
0.25×2.6×4
=0.25×4×2.6
=1×2.6
=2.6
15.8×101-15.8
=15.8×(101-1)
=15.8×100
=1580
8×(20-1.25)
=8×20-8×1.25
=160-10
=150
【点睛】本题考查了小数的四则混合运算和简便计算,整数的四则混合运算顺序和运算定律同样适用于小数。
27.见详解
【分析】用数对表示位置时,通常把竖排叫列,横排叫行。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
【详解】作图如下:
【点睛】一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。
28.(8,6);图见详解
【分析】根据用数对表示位置时,先表示第几列,再表示第几行即可解答。
【详解】由分析可得:后一个顶点所在的位置用数对表示可能为(8,6)
作图如下:
【点睛】本题主要考查用数对表示位置和梯形的认识。
29.见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此用数对表示出各个场所的位置,以学校为观测点,再根据“上北下南,左西右东”及距离解答即可;
(2)根据“上北下南,左西右东”及距离标出这两名同学家的位置;
(3)根据用数对表示位置的方法,找出各个场所的位置,进而描述王玲的活动路线即可。
【详解】(1)医院是,它在学校的以东800米,再往北200米处;少年宫是,它在学校的以东600米,再往北500米处;体育馆所在的位置可以用表示。它在学校以东300米,再往北600米处;邮局所在的位置可以用表示。它在学校以东100米,再往北700米处;公园所在的位置可以用表示。它在学校以东900米,再往北500米处;商场所在的位置可以用表示。它在学校以东700米,再往北900米处。
(2)如图:
(3)王玲从家出发到图书馆,再到少年宫,又去了体育馆,最后回到了家中。
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
30.(1)B(2,5),C(3,11)
(2)(3)见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此用数对表示出点B、C的位置即可;
(2)将三角形的各个顶点向下平移3个单位,再顺次连接各点即可;再根据用数对表示位置的方法表示出顶点A′、B′、C′的位置;
(3)将三角形的各个顶点向右平移5个单位,再顺次连接各点即可;再根据用数对表示位置的方法表示出顶点将三角形的各个顶点向下平移3个单位,再顺次连接各点即可;再根据用数对表示位置的方法表示出顶点A″、B″、C″的位置。
【详解】(1)如果A点的位置为(1,6),则B(2,5),C(3,11)。
(2)(3)如图所示:
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
31.(1)B(6,4);C(9,3);(2)A′(3,2);B′(1,1);C′(4,0)
【分析】(1)用数对表示位置时,前一个数表示第几列,后一个数表示第几行;
(2)根据平移的特征,把三角形ABC的各顶点分别先向左平移5格,再向下平移3格,依次连接即可得到平移后的三角形A′B′C′,再用数对表示三个顶点的位置。
【详解】(1)B(6,4),C(9,3);
(2)如图:
A′(3,2);B′(1,1);C′(4,0)。
【点睛】本题考查了图形的平移以及用数对表示位置的方法,平移作图要注意:①方向;②距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动。
32.(1)见详解
(2)(2,1) (3,3) (5,1)
(5,1) (6,3) (8,1)
【分析】(1)根据图形平移的方法,先把图中三角形的三个顶点向右平移3格,再把它们依次连接起来,即可得出平移后的三角形;
(2)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可标出三角形顶点的位置。
【详解】(1)如图如下:
(2)根据数对表示位置的方法,用数对表示三角形顶点分别是:
(2,1) (3,3) (5,1)(5,1) (6,3) (8,1)。
【点睛】此题考查了图形平移的方法以及数对表示位置的方法的灵活应用,掌握数对表示位置的方法是:第一个数字表示列,第二个数字表示行是解题关键。
33.(1)(12,6)
(2)(3)(4)见详解
【分析】(1)数对的括号中,第一个数字表示列,第二个数字表示行,据此解答。
(2)画轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(3)将三角形ABC的各点向右移动平移10格,然后连接即可。
(4)从点出发,向北方走,每分钟走50米,3分钟刚好到小刚家,也就是从D点开始,向上平移50×3=150(米),也就是3格,标注F即可。
【详解】(1)通过观察O点的位置,可知,是第12列,第6行,用数对表示(12,6)。
(2)(3)(4)如下图:
【点睛】此题主要考查学生对数对、物体平移和轴对称图形的认识与应用。
34.(1)图书馆的位置用数对(4,3)表示,在小军家以西200米,以北200米处;
少年宫的位置为(3,7),在小军家以西300米,以北600米处;
(2)见详解;
(3)小军家→图书馆→博物馆→少年宫→邮局→小军家
【分析】(1)根据例句,数对中第一个数表示列数,第二个数表示行数,先找到图书馆的位置用数对表示,再看在小军家以西2格,再往北2格,这里1格代表100米,算出实际距离为2×100=200米;同理描述少年宫。
(2)以小军家为观测点,根据“上北下南,左西右东”,判断方向,再根据1格代表100米,500米和300米分别代表几个100米就是几格,找到小明家位置。
(3)根据数对找出点所对应的地方,按顺序描述路线。
【详解】(1)图书馆位置(4,3)
在小军家以西:2×100=200(米)再往北:2×100=200(米);
少年宫位置(3,7)
在小军家以西:3×100=300(米)
再往北:6×100=600(米)
答:图书馆所在位置可以用(4,3)表示,它在小军家以西200米,再往北200米处;
少年宫所在位置可以用(3,7)表示,它在小军家以西300米,再往北600米处。
(2)500里面包含5个100;300里面有3个100。再根据“上北下南,左西右东”绘图找点。
(3)根据数对中第一个数表示列数,第二个数表示行数,知道(6,1)代表小军家,(4,3)表示图书馆;(5,5)表示博物馆;(3,7)代表少年宫;(2,5)代表邮局;(6,1)代表小军家。
故周末,小军的活动路线是:小军家→图书馆→博物馆→少年宫→邮局→小军家。
答案第1页,共2页
答案第1页,共2页
