苏教版五年级上册数学小数的意义(课件)(共22张PPT)
文档属性
| 名称 | 苏教版五年级上册数学小数的意义(课件)(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 07:02:34 | ||
图片预览







文档简介
(共22张PPT)
苏教版义务教育教科书小学数学五年级上册
小 数 的 意 义
观课的课眼
小数是十进分数,有了分数人类为什么还要捣腾出十进分数来?学习小数的意义,更为丰富的数学本质是什么?
学习小数,大家往往从“米、分米、厘米”或“元、角、分”间的互化入手,教学能不能充分利用学生关于整数意义的旧知,自然生长出小数意义的新知来,从而获得关于数的更为一般的认识?
【意义】yìyì [名] ①表示什么
②价值
0.2元
0.2元
1元
0.2米
0.2米
0.2
1米
个
十
百
千
十分之一
个
十
千
百
×10
×10
×10
……
÷10
÷10
÷10
÷10
百分之一
千分之一
÷10
÷10
……
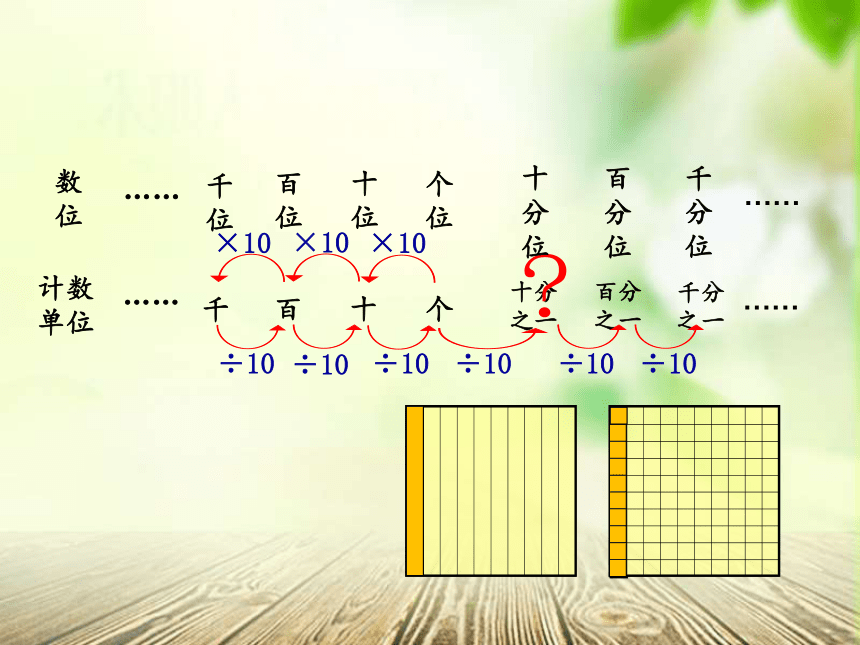
计数单位
数位
……
千位
百位
十位
个位
十分位
百分位
千分位
……
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
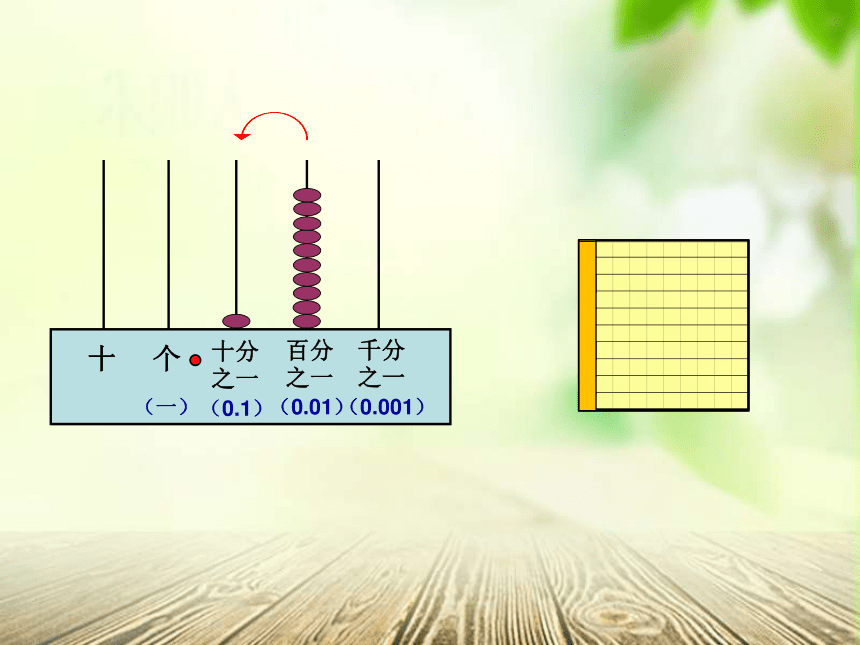
你能在计数器上直接拨出 吗?
1
2
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
“掉进分数计算里去了”
整数,计数单位相同,又能满十进一。但分数的分母不同,它的计数单位就不同。
遇上麻烦了!
小数,是人类促进计算发展的一个重要发明。
个
十
千
百
×10
×10
×10
……
÷10
÷10
÷10
÷10
画图可以把问题思考清楚。
把旧知识理透彻,有助于思考新问题。
小数的意义
一位小数表示十分之几
两位小数表示百分之几
三位小数表示千分之几
……
当新问题比较复杂的时候,可以分类研究。
课后分享
原有的经典教学安排
原有教学安排的主要特点
从米、分米、厘米切入,体会分数和小数间形式上的关系,从而揭示小数意义——是归纳的思路。推理过程:十分之一米=1分米,而1分米=0.1米,所以,十分之一米=0.1米。小数和分数间建立的联系是形式化的,并没有深入到数学的深处。
历史的本源面目
分数和自然数的历史一样古老,小数的产生远迟于它们。
历史上,分数计算苦不堪言。7世纪,若能计算八个分数加法的题,就是最尖端的数学技能了。直到18世纪,对分数计算还心有余悸。
随着经济的发展,关于零头(往往用分数表示)的计算越来越普遍,人们迫切希望商业中的所有计算都能像整数计算那么简单。
历史的本源面目
1585年,荷兰人斯蒂文《论十进》,在前言中说:简而言之,本书要讲授不使用分数怎样简便地完成各种账务结算和货币兑换,如果这种新计数系统的算术运算法则与整数的相关法则相通,便能起到这些效果。
小数的出现标志着十进计数法从整数扩展到了分数,使得分数和整数在形式上得到了统一。
小数意义的两个维度
一方面,是十进分数;另一方面,是十进制计数法的扩展。
用十进制计数法去统一整数和分数,在原有计数法则的旧知上,用演绎推理的力量让学生自我完成认知的突围,依照逻辑自我创造新的计数单位是0.1,0.01,0.001,小数意义的建构过程触及到了数的本质。
观课的课眼
小数是十进分数,有了分数人类为什么还要捣腾出十进分数来?学习小数的意义,更为丰富的数学本质是什么?
学习小数,大家往往从“米、分米、厘米”或“元、角、分”间的互化入手,教学能不能充分利用学生关于整数意义的旧知,自然生长出小数意义的新知来,从而获得关于数的更为一般的认识?
苏教版义务教育教科书小学数学五年级上册
小 数 的 意 义
观课的课眼
小数是十进分数,有了分数人类为什么还要捣腾出十进分数来?学习小数的意义,更为丰富的数学本质是什么?
学习小数,大家往往从“米、分米、厘米”或“元、角、分”间的互化入手,教学能不能充分利用学生关于整数意义的旧知,自然生长出小数意义的新知来,从而获得关于数的更为一般的认识?
【意义】yìyì [名] ①表示什么
②价值
0.2元
0.2元
1元
0.2米
0.2米
0.2
1米
个
十
百
千
十分之一
个
十
千
百
×10
×10
×10
……
÷10
÷10
÷10
÷10
百分之一
千分之一
÷10
÷10
……
计数单位
数位
……
千位
百位
十位
个位
十分位
百分位
千分位
……
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
你能在计数器上直接拨出 吗?
1
2
个
十
十分之一
百分之一
(0.1)
(0.01)
(一)
千分之一
(0.001)
“掉进分数计算里去了”
整数,计数单位相同,又能满十进一。但分数的分母不同,它的计数单位就不同。
遇上麻烦了!
小数,是人类促进计算发展的一个重要发明。
个
十
千
百
×10
×10
×10
……
÷10
÷10
÷10
÷10
画图可以把问题思考清楚。
把旧知识理透彻,有助于思考新问题。
小数的意义
一位小数表示十分之几
两位小数表示百分之几
三位小数表示千分之几
……
当新问题比较复杂的时候,可以分类研究。
课后分享
原有的经典教学安排
原有教学安排的主要特点
从米、分米、厘米切入,体会分数和小数间形式上的关系,从而揭示小数意义——是归纳的思路。推理过程:十分之一米=1分米,而1分米=0.1米,所以,十分之一米=0.1米。小数和分数间建立的联系是形式化的,并没有深入到数学的深处。
历史的本源面目
分数和自然数的历史一样古老,小数的产生远迟于它们。
历史上,分数计算苦不堪言。7世纪,若能计算八个分数加法的题,就是最尖端的数学技能了。直到18世纪,对分数计算还心有余悸。
随着经济的发展,关于零头(往往用分数表示)的计算越来越普遍,人们迫切希望商业中的所有计算都能像整数计算那么简单。
历史的本源面目
1585年,荷兰人斯蒂文《论十进》,在前言中说:简而言之,本书要讲授不使用分数怎样简便地完成各种账务结算和货币兑换,如果这种新计数系统的算术运算法则与整数的相关法则相通,便能起到这些效果。
小数的出现标志着十进计数法从整数扩展到了分数,使得分数和整数在形式上得到了统一。
小数意义的两个维度
一方面,是十进分数;另一方面,是十进制计数法的扩展。
用十进制计数法去统一整数和分数,在原有计数法则的旧知上,用演绎推理的力量让学生自我完成认知的突围,依照逻辑自我创造新的计数单位是0.1,0.01,0.001,小数意义的建构过程触及到了数的本质。
观课的课眼
小数是十进分数,有了分数人类为什么还要捣腾出十进分数来?学习小数的意义,更为丰富的数学本质是什么?
学习小数,大家往往从“米、分米、厘米”或“元、角、分”间的互化入手,教学能不能充分利用学生关于整数意义的旧知,自然生长出小数意义的新知来,从而获得关于数的更为一般的认识?
