江苏省泰州市姜堰区实验初级中学2024-2025学年九年级上学期9月月考数学试题(无答案)
文档属性
| 名称 | 江苏省泰州市姜堰区实验初级中学2024-2025学年九年级上学期9月月考数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 00:00:00 | ||
图片预览


文档简介
2024年秋九年级数学独立作业
满分:150分,完成时间:120分钟
一 .选择题(共6小题,每题3分)
1.方程x =4 的解是( )
A.x =4,x =-4 B.x =x =2 C.x =2,x =-2 D.x =1,x =4
2. 如图所示的网格由边长相同的小正方形组成,点A、B、C.D、E、F、G 在小正方形的顶点上,则△ABC 的外心是( )
A. 点 D B. 点 E C. 点 F D. 点 G
3.用配方法解方程x +8x+7=0, 则配方正确的是( )
A.(x+4) =9 B.(x-4) =9 C.(x-8) =16 D.(x+8) =57
4.电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房 按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x, 则方程可以列为( )
A.2+2x+2x =18 B.2(1+x) =18
C.(1+x) =18 D.2+2(I+x)+2(1+x) =18
5. 在 Rt△ABC中,∠C=90°,BC=3,AC=4,D 为AB的中点. 以A为圆心,r 为半径作OA, 若 B 、C、
D 三点中只有一点在OA内,则OA 的半径r 的取值范围是( )
A.2.56 如图,已知直线PA 交O0 于A、B 两点,AE 是⊙0的直径,点C 为⊙0上一点,且AC 平分∠PAE, 过 C 作CD⊥PA, 垂足为D, 且 DC+DA=12, O0 的直径为20,则AB 的长等于( )
A.8 B.12 C.16 D.18
(2) (6) (8) (9) (10) 二 .填空题(共10小题,每题3分)
7.已知一元二次方程x -5x+m=0 的一个根为x =1, 则另一个根x 的值为
8. 如图,AB是O0 的直径,BC 是O0 的弦,若∠OBC=60°, 则 ∠BAC=
9.如图,在△ABC中,∠C=45°,AB=2,00 为△ABC的外接圆,则O0 的半径为
10.如图,⊙0的半径为2,弦AB=2√3, 则 OC 的长为
第1页(共4页)
11. 已知点A,B,C 在00上,若∠AOC=100°, 则∠ABC 的度数为
12.对于任意实数a,b; 我们定义新运算“*”:a*b=a +2ab-b , 例如3*5=3 +2×3×5-5 =14.若m; n 是方程(x+2)*3=0 的两根,则的值为
(
·
)13. 已 知 , 则 的值为
14.已知关于x的一元二次方程c(1-x )-2bx=a(1+x ), 其中a、b、c分别为△ABC三边的长,如果方 程有两个相等的实数根,则△ABC 的形状为
15.一条排水管的截面如图所示,已知排水管的半径OA=50cm, 水面宽AB=60cm, 某天下雨后,水面宽度
变为80cm, 则此时排水管水面上升了 cm.
16.如图,在等腰直角△ABC中,斜边AB 的长度为8,以AC 为直径作圆,点P 为半圆上的动点,连接BP,
取 BP 的中点M, 则 CM 的最小值为
(15)
16)
解答题(共10小题,共102分)
(16分)解方程:
(1)2x =2; (2)2x -3x-3=0
(3)x -2x-7=0; (4)3x(x-1)=1-x.
18. (8分)关于x 的方程,x -2x+4-m=0有两个不等的实数根.
(1)求m 的取值范围;
(2)化简:
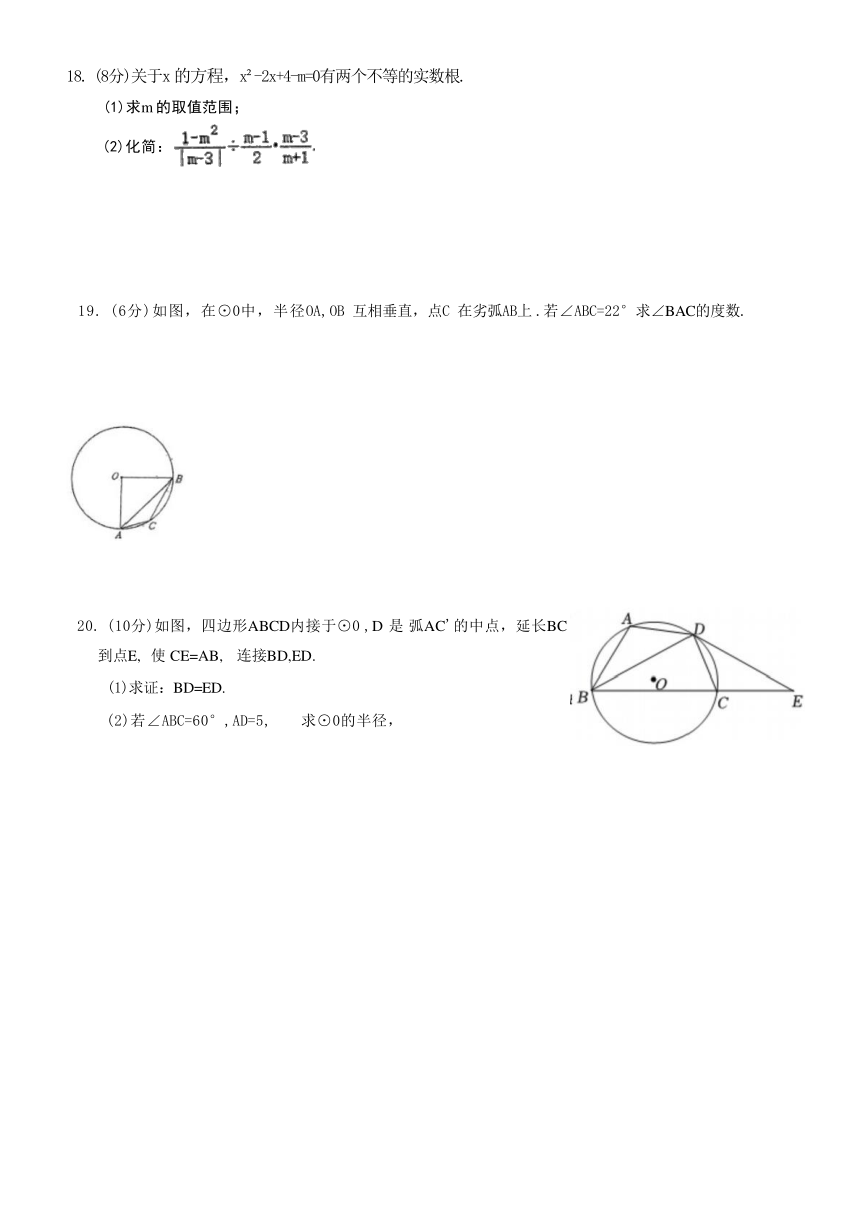
19. (6分)如图,在⊙0中,半径OA,OB 互相垂直,点C 在劣弧AB上 .若∠ABC=22°求∠BAC的度数.
20. (10分)如图,四边形ABCD内接于⊙0 ,D 是 弧AC'的中点,延长BC 到点E, 使 CE=AB, 连接BD,ED.
(1)求证:BD=ED.
(2)若∠ABC=60°,AD=5, 求⊙0的半径,
21. (10分)果农小明原计划以每千克4元的卑价销售某种水果,由于部分果农盲目扩大种植,造成该水果 代销,张远为了加快销售,减少损失,经过两次下调价格后,以每千克2.56元的单价销售.
(1)求平均每次下调价格的百分率;
(2)若小明第一次下调价格后卖出3吨该水果,第二次下调价格后又卖出2吨该水果,问小明共获得销 售款多少元
(
是
AC
的中点,
)22. (10分)如图,四边形ABCD 是00的内接四边形,∠ADC=2∠B, 点 D
(1)求∠B的度数
(2)求证:四边形AOCD是菱形.
23. (8分)如图,在平面直角坐标系x0y 中 ,A(0,4)、B(-4,4)、C(-6,2).
(1)在图中画出经过A、B、C 三点的圆弧所在圆的圆心M 的位置,并写
出圆心M 的坐标
(2)OM 的平径为
(3)点O 到OM 上最近的点的距离为
24. (8分)如图,点P 是⊙0内一定点.
(1)过点P 作弦AB, 使点P 是AB的中点(不写作法,保留作图痕迹);
(2)若⊙0的半径为10,OP=6,
①求过点P 的弦的长度m 范围;
②过 点P 的弦中,长度为整数的弦有 条.
25. (12分)根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1 某农户承包了一块长方形果园ABCD,图1是 果园的平面图,其中AB=200米,BC=300 米,准备在它的四周铺设道路,上下两条横向 道路的宽度都为2x米,左右两条纵向道路的 宽度都为x米,中间部分种植水果. 出于货车通行等因素的考虑,道路宽度x不超 过12米,且不小于5米.
素材2 该农户发现某一种草莓销售前景比较不错,经 市场调查,草莓培育一年可产果.若每平方米 的草莓销售平均利润为100元,每月可销售 5000平方米的草莓;受天气原因,农户为了快 速将草莓出手,决定降价,若每平方米草莓平 均利润下调4元,每月可多销售500平方米草 莓,果园每月的承包费为2万元. (图2)
问题解决
任务1 解决果园中路面宽度的设计对种植面积的影 响 . (1)请直接写出纵向道路宽度x的取值 范围 . (2)若中间种植的面积是44800m ,则 路面设置的宽度是否符合要求.
任务2 解决果园种植的预期利润问题. (总利润=销售利润-承包费) (3)若农户预期一个月的总利润为55.2 方元,则从购买草莓客户的角度考虑, 每平方米草莓平均利润应该降价多少 元
26. (14分)如图,O0 是等边△ABC 的外接圆,P 点是⊙0劣弧AB 上的一个动点(不与点A,B 重合)。
(1)求∠APB的度数;
(2)若PA=3,PB=4, 求PC 的长;
(3)若AB=4√3, 点P 在劣弧AB上运动的过程中,
①PA+PB 的值是否为定值,若是,请求出这个定值;若不是,求出其 值的取值范围。
②试探究PA +PB +PC 的值是否为定值,若是,请求出这个定值;若不 是,求出其的取值范围。
满分:150分,完成时间:120分钟
一 .选择题(共6小题,每题3分)
1.方程x =4 的解是( )
A.x =4,x =-4 B.x =x =2 C.x =2,x =-2 D.x =1,x =4
2. 如图所示的网格由边长相同的小正方形组成,点A、B、C.D、E、F、G 在小正方形的顶点上,则△ABC 的外心是( )
A. 点 D B. 点 E C. 点 F D. 点 G
3.用配方法解方程x +8x+7=0, 则配方正确的是( )
A.(x+4) =9 B.(x-4) =9 C.(x-8) =16 D.(x+8) =57
4.电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房 按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x, 则方程可以列为( )
A.2+2x+2x =18 B.2(1+x) =18
C.(1+x) =18 D.2+2(I+x)+2(1+x) =18
5. 在 Rt△ABC中,∠C=90°,BC=3,AC=4,D 为AB的中点. 以A为圆心,r 为半径作OA, 若 B 、C、
D 三点中只有一点在OA内,则OA 的半径r 的取值范围是( )
A.2.5
A.8 B.12 C.16 D.18
(2) (6) (8) (9) (10) 二 .填空题(共10小题,每题3分)
7.已知一元二次方程x -5x+m=0 的一个根为x =1, 则另一个根x 的值为
8. 如图,AB是O0 的直径,BC 是O0 的弦,若∠OBC=60°, 则 ∠BAC=
9.如图,在△ABC中,∠C=45°,AB=2,00 为△ABC的外接圆,则O0 的半径为
10.如图,⊙0的半径为2,弦AB=2√3, 则 OC 的长为
第1页(共4页)
11. 已知点A,B,C 在00上,若∠AOC=100°, 则∠ABC 的度数为
12.对于任意实数a,b; 我们定义新运算“*”:a*b=a +2ab-b , 例如3*5=3 +2×3×5-5 =14.若m; n 是方程(x+2)*3=0 的两根,则的值为
(
·
)13. 已 知 , 则 的值为
14.已知关于x的一元二次方程c(1-x )-2bx=a(1+x ), 其中a、b、c分别为△ABC三边的长,如果方 程有两个相等的实数根,则△ABC 的形状为
15.一条排水管的截面如图所示,已知排水管的半径OA=50cm, 水面宽AB=60cm, 某天下雨后,水面宽度
变为80cm, 则此时排水管水面上升了 cm.
16.如图,在等腰直角△ABC中,斜边AB 的长度为8,以AC 为直径作圆,点P 为半圆上的动点,连接BP,
取 BP 的中点M, 则 CM 的最小值为
(15)
16)
解答题(共10小题,共102分)
(16分)解方程:
(1)2x =2; (2)2x -3x-3=0
(3)x -2x-7=0; (4)3x(x-1)=1-x.
18. (8分)关于x 的方程,x -2x+4-m=0有两个不等的实数根.
(1)求m 的取值范围;
(2)化简:
19. (6分)如图,在⊙0中,半径OA,OB 互相垂直,点C 在劣弧AB上 .若∠ABC=22°求∠BAC的度数.
20. (10分)如图,四边形ABCD内接于⊙0 ,D 是 弧AC'的中点,延长BC 到点E, 使 CE=AB, 连接BD,ED.
(1)求证:BD=ED.
(2)若∠ABC=60°,AD=5, 求⊙0的半径,
21. (10分)果农小明原计划以每千克4元的卑价销售某种水果,由于部分果农盲目扩大种植,造成该水果 代销,张远为了加快销售,减少损失,经过两次下调价格后,以每千克2.56元的单价销售.
(1)求平均每次下调价格的百分率;
(2)若小明第一次下调价格后卖出3吨该水果,第二次下调价格后又卖出2吨该水果,问小明共获得销 售款多少元
(
是
AC
的中点,
)22. (10分)如图,四边形ABCD 是00的内接四边形,∠ADC=2∠B, 点 D
(1)求∠B的度数
(2)求证:四边形AOCD是菱形.
23. (8分)如图,在平面直角坐标系x0y 中 ,A(0,4)、B(-4,4)、C(-6,2).
(1)在图中画出经过A、B、C 三点的圆弧所在圆的圆心M 的位置,并写
出圆心M 的坐标
(2)OM 的平径为
(3)点O 到OM 上最近的点的距离为
24. (8分)如图,点P 是⊙0内一定点.
(1)过点P 作弦AB, 使点P 是AB的中点(不写作法,保留作图痕迹);
(2)若⊙0的半径为10,OP=6,
①求过点P 的弦的长度m 范围;
②过 点P 的弦中,长度为整数的弦有 条.
25. (12分)根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1 某农户承包了一块长方形果园ABCD,图1是 果园的平面图,其中AB=200米,BC=300 米,准备在它的四周铺设道路,上下两条横向 道路的宽度都为2x米,左右两条纵向道路的 宽度都为x米,中间部分种植水果. 出于货车通行等因素的考虑,道路宽度x不超 过12米,且不小于5米.
素材2 该农户发现某一种草莓销售前景比较不错,经 市场调查,草莓培育一年可产果.若每平方米 的草莓销售平均利润为100元,每月可销售 5000平方米的草莓;受天气原因,农户为了快 速将草莓出手,决定降价,若每平方米草莓平 均利润下调4元,每月可多销售500平方米草 莓,果园每月的承包费为2万元. (图2)
问题解决
任务1 解决果园中路面宽度的设计对种植面积的影 响 . (1)请直接写出纵向道路宽度x的取值 范围 . (2)若中间种植的面积是44800m ,则 路面设置的宽度是否符合要求.
任务2 解决果园种植的预期利润问题. (总利润=销售利润-承包费) (3)若农户预期一个月的总利润为55.2 方元,则从购买草莓客户的角度考虑, 每平方米草莓平均利润应该降价多少 元
26. (14分)如图,O0 是等边△ABC 的外接圆,P 点是⊙0劣弧AB 上的一个动点(不与点A,B 重合)。
(1)求∠APB的度数;
(2)若PA=3,PB=4, 求PC 的长;
(3)若AB=4√3, 点P 在劣弧AB上运动的过程中,
①PA+PB 的值是否为定值,若是,请求出这个定值;若不是,求出其 值的取值范围。
②试探究PA +PB +PC 的值是否为定值,若是,请求出这个定值;若不 是,求出其的取值范围。
同课章节目录
