青岛版(六三制)数学八年级上册 2.2轴对称的基本性质 课件(共20张PPT)
文档属性
| 名称 | 青岛版(六三制)数学八年级上册 2.2轴对称的基本性质 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-28 22:02:12 | ||
图片预览








文档简介
(共20张PPT)
轴对称的基本性质
温故知新
1.过点P作直线
的垂线。
(1)
(5)
2.观察下列每组全等图形,哪组变化是轴对称?其它图形是什么变化?
(4)
(3)
(6)
(2)
温故知新
(1)
(3)
(6)
上节课我们用了什么方法,找出△ABC关于直线
成轴对称的图形?
思考:
温故知新
3 .图中两个三角形关于直线 成轴对称。如果三角形的部
分边长和角的度数如图所示,说出未知的边长和角的度数。
创设情景:
如何在黑板上等折叠、扎孔不方便的情境下
找出△ABC关于直线 的成轴对称的图形?
如何利用轴对称的基本性质设计出
漂亮的轴对称图案?
新课来啦
学习目标:
1.经历探索轴对称的基本性质的过程,理解轴对称的基本性质。
2.能画出简单平面图形关于给定对称轴的对称图形。
活动一:实验与探究
做一做
(1)把一张纸片对折,扎一个小孔,然后展开铺平,记得到的两个
小孔为点A与A′,折痕为MN,连接AA′交MN于点O。
A
A′
o
M
N
(2)如果将纸片沿MN重新折叠,线段OA与OA′有怎样的
大小关系?线段AA′与直线MN有怎样的位置关系 ?猜想一下。
猜一猜
量一量
说一说
利用折叠重合的知识说明以上结论成立的理由。(小组交流)
OA=OA′, AA′⊥MN。
用刻度尺和半圆仪量一量,
和你的猜想是否一致?
快速 高效
A
A′
B
B′
C
C′
M
N
活动一:实验与探究
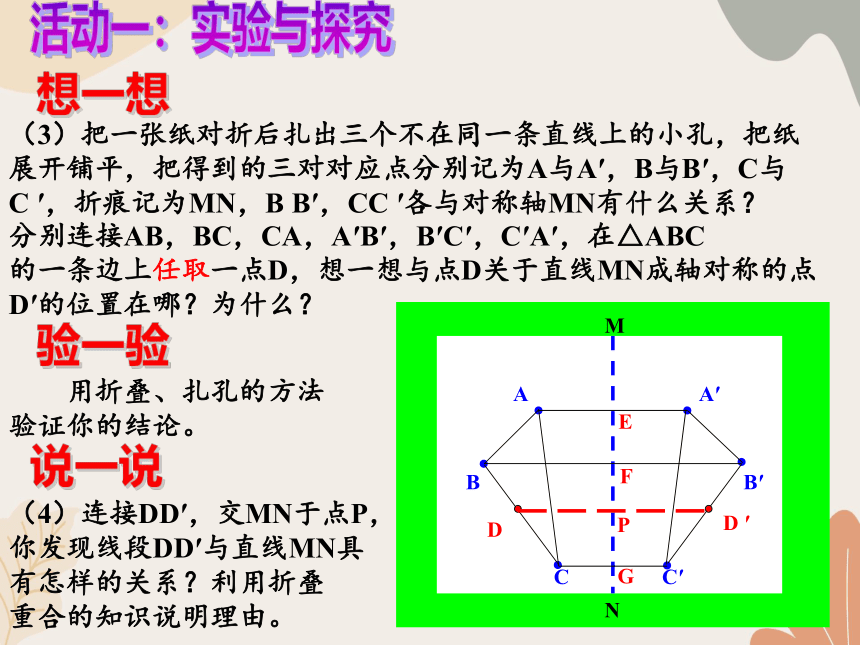
(3)把一张纸对折后扎出三个不在同一条直线上的小孔,把纸
展开铺平,把得到的三对对应点分别记为A与A′,B与B′,C与
C ′,折痕记为MN,B B′,CC ′各与对称轴MN有什么关系?
想一想
用折叠、扎孔的方法
验证你的结论。
验一验
(4)连接DD′,交MN于点P,
你发现线段DD′与直线MN具
有怎样的关系?利用折叠
重合的知识说明理由。
说一说
D
D ′
P
分别连接AB,BC,CA,A′B′,B′C′,C′A′,在△ABC
的一条边上任取一点D,想一想与点D关于直线MN成轴对称的点
D′的位置在哪?为什么?
G
E
F
A
A′
B
B′
C
C′
M
N
得出结论:
D
D ′
P
通过以上探究,我们可以归纳出:
成轴对称的两个图形中,
对应点的连线被对称轴 。
垂直平分
1.经历探索轴对称的基本性质的过程,理解轴对称的基本性质。
G
E
F
探究
方法
由简单到复杂
由特殊到一般
小测试
l
D
E
F
把图中的两个三角形的对应顶点分别相连接,说出哪些线段被直线 垂直平分。
A
B
C
2.能画出简单平面图形关于给定对称轴
的对称图形。
(1)如图,你能利用轴对称的性质,画出点A关于直线MN的对称点吗?
交流发现
(2)你能说明(1)中画一个已知点关于给定直线的对称点的方法的道理吗?
作垂线,取相等。
A
M
N
A′
请总结关键步骤可分几步。
点A′就是所求点。
(小组内交流你的方法。)
画出点A关于直线MN的对称点
A
M
N
变式训练
做在练习本上(2分钟)
(3)如图,你能画出与线段AB关于直线l 成轴对称的线段吗?能画出与直线AB关于直线l成轴对称的直线吗?
交流发现
A
B
L
例1:
如图,画出△BCD关于直线l的成轴对称的图形。
B′
C
C′
B
D
l
△ B′C′D就是求作的图形。
巩固练习
M
N
选代表,作垂线,
取相等,连顶点。
2.能画出简单平面图形关于给定对称轴的对称图形。
请总结关键步骤可分几步。
中国传统文化博大精深,是中华民族几千年的文化积淀而成的,剪纸艺术就是其中之一。下图中的两幅作品设计的依据是什么?
学以致用
动手撕一个简单的作品,并找出一组对应点说一说对应点的连线与对称轴的关系。
由简单到复杂
由特殊到一般
选代表,作垂线,
取相等,连顶点。
基本性质:垂直
平分
课堂小结
请你总结一下学到的数学知识,解题
思路和探究方法。
数学
知识
解题
思路
探究
方法
知
识
树
1.下列说法中,正确的是( )
A.若A、B关于直线MN对称,则AB垂直平分MN;
B.全等三角形是关于某直线对称的;
C.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧;
D.关于某直线对称的两个三角形是全等三角形。
2.课本36页练习第2题:画出△ABC关于直线l成轴对称的图形。
D
当堂达标
A
B
C
l
如图要在自来水管道 上修建一个水站分别向A、B两个村子供水,
请你在 上选择水厂的位置P,使铺设的管道
最短?
拓展延伸
谢 谢
轴对称的基本性质
温故知新
1.过点P作直线
的垂线。
(1)
(5)
2.观察下列每组全等图形,哪组变化是轴对称?其它图形是什么变化?
(4)
(3)
(6)
(2)
温故知新
(1)
(3)
(6)
上节课我们用了什么方法,找出△ABC关于直线
成轴对称的图形?
思考:
温故知新
3 .图中两个三角形关于直线 成轴对称。如果三角形的部
分边长和角的度数如图所示,说出未知的边长和角的度数。
创设情景:
如何在黑板上等折叠、扎孔不方便的情境下
找出△ABC关于直线 的成轴对称的图形?
如何利用轴对称的基本性质设计出
漂亮的轴对称图案?
新课来啦
学习目标:
1.经历探索轴对称的基本性质的过程,理解轴对称的基本性质。
2.能画出简单平面图形关于给定对称轴的对称图形。
活动一:实验与探究
做一做
(1)把一张纸片对折,扎一个小孔,然后展开铺平,记得到的两个
小孔为点A与A′,折痕为MN,连接AA′交MN于点O。
A
A′
o
M
N
(2)如果将纸片沿MN重新折叠,线段OA与OA′有怎样的
大小关系?线段AA′与直线MN有怎样的位置关系 ?猜想一下。
猜一猜
量一量
说一说
利用折叠重合的知识说明以上结论成立的理由。(小组交流)
OA=OA′, AA′⊥MN。
用刻度尺和半圆仪量一量,
和你的猜想是否一致?
快速 高效
A
A′
B
B′
C
C′
M
N
活动一:实验与探究
(3)把一张纸对折后扎出三个不在同一条直线上的小孔,把纸
展开铺平,把得到的三对对应点分别记为A与A′,B与B′,C与
C ′,折痕记为MN,B B′,CC ′各与对称轴MN有什么关系?
想一想
用折叠、扎孔的方法
验证你的结论。
验一验
(4)连接DD′,交MN于点P,
你发现线段DD′与直线MN具
有怎样的关系?利用折叠
重合的知识说明理由。
说一说
D
D ′
P
分别连接AB,BC,CA,A′B′,B′C′,C′A′,在△ABC
的一条边上任取一点D,想一想与点D关于直线MN成轴对称的点
D′的位置在哪?为什么?
G
E
F
A
A′
B
B′
C
C′
M
N
得出结论:
D
D ′
P
通过以上探究,我们可以归纳出:
成轴对称的两个图形中,
对应点的连线被对称轴 。
垂直平分
1.经历探索轴对称的基本性质的过程,理解轴对称的基本性质。
G
E
F
探究
方法
由简单到复杂
由特殊到一般
小测试
l
D
E
F
把图中的两个三角形的对应顶点分别相连接,说出哪些线段被直线 垂直平分。
A
B
C
2.能画出简单平面图形关于给定对称轴
的对称图形。
(1)如图,你能利用轴对称的性质,画出点A关于直线MN的对称点吗?
交流发现
(2)你能说明(1)中画一个已知点关于给定直线的对称点的方法的道理吗?
作垂线,取相等。
A
M
N
A′
请总结关键步骤可分几步。
点A′就是所求点。
(小组内交流你的方法。)
画出点A关于直线MN的对称点
A
M
N
变式训练
做在练习本上(2分钟)
(3)如图,你能画出与线段AB关于直线l 成轴对称的线段吗?能画出与直线AB关于直线l成轴对称的直线吗?
交流发现
A
B
L
例1:
如图,画出△BCD关于直线l的成轴对称的图形。
B′
C
C′
B
D
l
△ B′C′D就是求作的图形。
巩固练习
M
N
选代表,作垂线,
取相等,连顶点。
2.能画出简单平面图形关于给定对称轴的对称图形。
请总结关键步骤可分几步。
中国传统文化博大精深,是中华民族几千年的文化积淀而成的,剪纸艺术就是其中之一。下图中的两幅作品设计的依据是什么?
学以致用
动手撕一个简单的作品,并找出一组对应点说一说对应点的连线与对称轴的关系。
由简单到复杂
由特殊到一般
选代表,作垂线,
取相等,连顶点。
基本性质:垂直
平分
课堂小结
请你总结一下学到的数学知识,解题
思路和探究方法。
数学
知识
解题
思路
探究
方法
知
识
树
1.下列说法中,正确的是( )
A.若A、B关于直线MN对称,则AB垂直平分MN;
B.全等三角形是关于某直线对称的;
C.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧;
D.关于某直线对称的两个三角形是全等三角形。
2.课本36页练习第2题:画出△ABC关于直线l成轴对称的图形。
D
当堂达标
A
B
C
l
如图要在自来水管道 上修建一个水站分别向A、B两个村子供水,
请你在 上选择水厂的位置P,使铺设的管道
最短?
拓展延伸
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
