人教版2024-2025学年九年级数学上册22.3实际问题与二次函数拔高提升同步练习(附答案解析)
文档属性
| 名称 | 人教版2024-2025学年九年级数学上册22.3实际问题与二次函数拔高提升同步练习(附答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 21:59:08 | ||
图片预览



文档简介
人教版2024-2025学年九年级数学上册 22.3 实际问题与二次函数
拔高提升同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.关于二次函数,下列说法正确的是( )
A.图象与y轴的交点坐标为 B.图象的对称轴在y轴的左侧
C.图象与x轴没有交点 D.y的最大值为4
2.一个运动员打高尔夫球,若球的飞行高度y(m)与水平距离x(m)之间的函数表达式为:y(x﹣25)2+12,则高尔夫球在飞行过程中的最大高度为( )m.
A.12 B.25 C.13 D.14
3.烟花厂某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣2t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.10s
4.进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为( )
A. B. C. D.
5.如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )
A.1 m B.2 m C.3 m D.6 m
6.如图,隧道的截面由抛物线和长方形构成.长方形的长为,宽为,抛物线的最高点离路面的距离为.在如图所示的直角坐标系中,该抛物线的函数表达式可表示为( )
A. B. C. D.
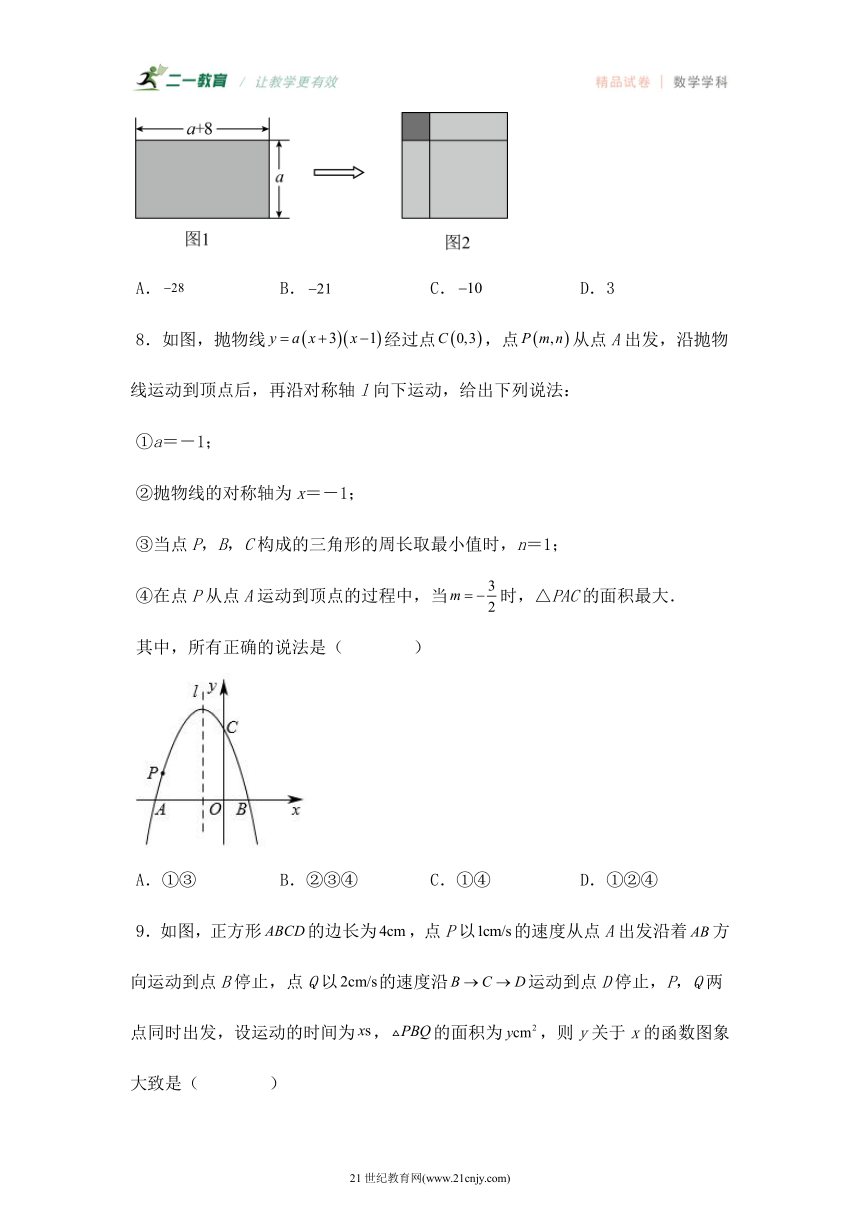
7.如图1,一张边长为、(为正整数)的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
8.如图,抛物线经过点,点从点A出发,沿抛物线运动到顶点后,再沿对称轴l向下运动,给出下列说法:
①a=-1;
②抛物线的对称轴为x=-1;
③当点P,B,C构成的三角形的周长取最小值时,n=1;
④在点P从点A运动到顶点的过程中,当时,△PAC的面积最大.
其中,所有正确的说法是( )
A.①③ B.②③④ C.①④ D.①②④
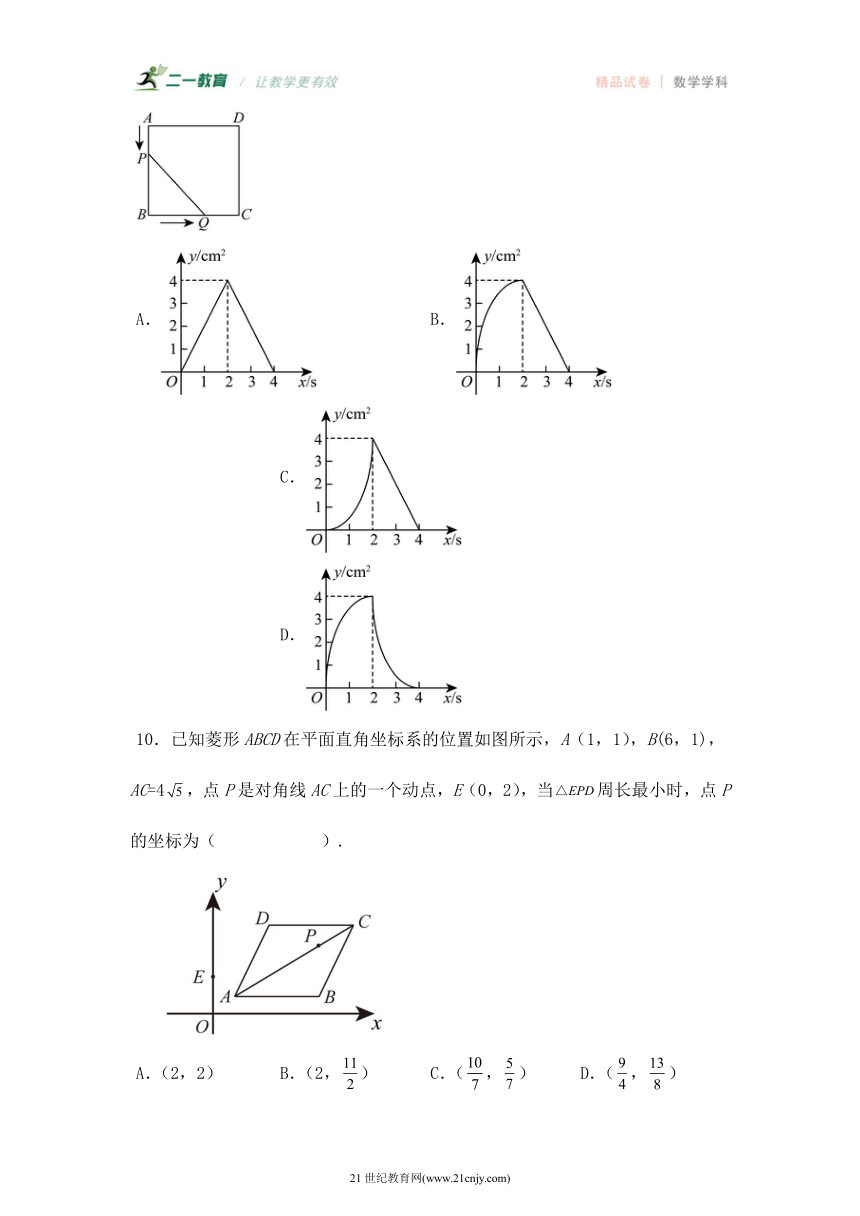
9.如图,正方形的边长为,点P以的速度从点A出发沿着方向运动到点B停止,点Q以的速度沿运动到点D停止,P,Q两点同时出发,设运动的时间为,的面积为,则y关于x的函数图象大致是( )
A. B. C. D.
10.已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4,点P是对角线AC上的一个动点,E(0,2),当周长最小时,点P的坐标为( ).
A.(2,2) B.(2,) C.(,) D.(,)
二、填空题
11.某超市一月份的营业额为200万元,一月、二月、三月的营业额共y万元,如果平均每月增长率为x,则营业额y与月平均增长率x之间的函数关系式为 .
12.将抛物线先向左平移2个单位长度,再向上平移个单位长度.若得到的抛物线经过点,则的值是 .
13.实心球是一项以力量为基础,以动作速度为核心的投掷项目.如图,某次比赛中运动员站在O处将实心球从B处抛出,它的运动路线可以看作是抛物线的一部分.若实心球在运动过程中最高离地面3米,此时与运动员的水平距离为4米,则该运动员投掷实心球的水平距离OA为 米.
14.如图,已知二次函数的图像与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知的面积是6,若在抛物线上存在一点P(与点C不重合),使,则点P的坐标为 .
15.如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.若点D为抛物线上一点且横坐标为,点E为y轴上一点,点F在以点A为圆心,2为半径的圆上,则的最小值 .
三、解答题
16.冬季天气干燥,空气加湿器得以畅销,某商场销售一种空气加湿器,进价是每台元,月销售量(台)与售价(元台)满足一次函数关系式.若某月规定该商场的这种空气加湿器的售价不低于进价且不高于元台,则该商场该月销售这种空气加湿器获得的最大利润是多少元?
17.某中学组织开展“回顾党史,重温初心”的红色研学旅行,估计人数在之间.甲、乙两家旅行社原价均为元/人,甲旅行社优惠方案:所有人八折优惠;乙旅行社优惠方案:人以内(含人)按原价收费,超过的人数每人费用降低.
(1)分别写出两家旅行社旅行费用(元)与人数之间的函数关系式;
(2)若有人参加旅游,选择哪家旅行社比较划算?
18.阅读以下材料,完成课题研究任务:
【研究课题】设计公园喷水池
【素材】某公园计划修建一个图所示的喷水池,水池中心处立着一个高为的实心石柱,水池周围安装一圈喷头,使得水流在各个方向上都沿形状相同的抛物线喷出,并在石柱顶点处汇合为使水流形状更漂亮,要求水流在距离石柱处能达到最大高度,且离池面的高度为.
【素材】距离池面米的位置,围绕石柱还修了一个小水池,要求小水池不能影响水流.
【任务解决】
(1)小张同学设计的水池半径为,请你结合已学知识,判断他设计的水池是否符合要求.
(2)为了不影响水流,小水池的半径不能超过多少米?
19.某数学活动小组研究一款如图①简易电子体重秤,当人踏上体重秤的踏板后,读数器可以显示人的质量(单位:).图②是该秤的电路图,已知串联电路中,电流(单位:)与定值电阻.可变电阻(单位:)之间关系为 ,电源电压恒为, 定值电阻的阻值为.
根据与之间的关系得出一组数据如下:
… 1 2 3 q 6 …
4 p 2
(1)填空: , ;
(2)该小组把上述问题抽象为数学模型,请根据表中数据在图③中描出实数对的对应点,画出函数 的图象,并写出一条此函数图象关于增减性的性质.
(3)若电流表量程是,可变电阻与踏板上人的质量之间函数关系如图④所示,为保护电流表,求电子体重秤可称的最大质量为多少千克?
20.如图,已知抛物线与轴的一个交点为,另一个交点为,与轴的交点为,其顶点为,对称轴为直线.
(1)求抛物线的解析式;
(2)已知点为轴上的一个动点,当是以为一腰的等腰三角形时,求点M的坐标.
21.某超市以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)之间满足一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)当每千克干果降价3元时,超市获利多少元?
(3)若超市要想获利2090元,且让顾客获得更大实惠,这种干果每千克应降价多少元?
22.如图(1)中,,,,的平分线交于,过点作与垂直的直线.动点从点出发沿折线以每秒个单位长度的速度向终点运动,运动时间为秒,同时动点从点出发沿折线以相同的速度运动,当点到达点时、同时停止运动.
(1)求、的长;
(2)设的面积为,求与的函数关系式,并求出自变量的取值范围.
23.定义:如果四边形的一条对角线把这个四边形分成面积相等的两个三角形,那么这个四边形叫做和谐四边形,这条对角线叫做和谐对角线,
[概念理解]
(1)下列图形中,属于和谐四边形的是____________.
A.平行四边形 B.对角线互相垂直的四边形 C.对角线相等的四边形
[性质探讨];
(2)和谐四边形的性质:在和谐四边形中,和谐对角线平分另一条对角线.利用所学知识证明和谐四边形的性质,即:
如图1,已知:四边形是和谐四边形,和谐对角线与对角线交于点与的面积相等.求证:.
[探究应用];
(3)①如图2,已知四边形是和谐四边形,和谐对角线与对角线交于点.求证:;
②如图3,已知直线与抛物线交于两点,点在轴负半轴上,满足,点在第一象限且位于抛物线上,若四边形是和谐四边形,求点的横坐标.
21世纪教育网(www.21cnjy.com)
1.D
【分析】根据二次函数的性质及与坐标轴的交点问题依次判断即可.
【详解】解:A、∵二次函数,
当时,,
∴与y轴交点坐标为,选项说法错误,不符合题意;
B、
∵对称轴为,
∴对称轴在y轴右侧,选项说法错误,不符合题意;
C、当时,,
,
∴图象与x轴有两个交点,选项说法错误,不符合题意;
D、∵,有最大值,
当时,,
∴顶点坐标为,y有最大值4,选项说法正确,符合题意;
故选:D.
【点睛】本题主要考查了二次函数的性质,解答本题的关键是熟练掌握二次函数图象的顶点坐标,对称轴以及开口方向等,此题难度不大.
2.A
【分析】直接根据二次函数的图象及性质即可得出答案.
【详解】解:∵y(x﹣25)2+12,
顶点坐标为(25,12),
∵0,
∴当x=25时,y有最大值,最大值为12.
故选:A.
【点睛】本题主要考查二次函数的最大值,掌握二次函数的图象和性质是解题的关键.
3.C
【分析】将h关于t的函数关系式变形为顶点式,即可得出升到最高点的时间,从而得出结论.
【详解】解:∵h=﹣2t2+20t+1=﹣2(t﹣5)2+51,
∴当t=5时,礼炮升到最高点.
故选:C.
【点睛】本题考查了二次函数的应用,解题的关键是将二次函数的关系式变形为顶点式.本题属于基础题,难度不大,解决该题型题目时,将函数的关系式进行变换找出顶点坐标即可.
4.D
【分析】设平均每次降价的百分率是x,,第一次降价后的价格为,第二次降价的价格为,根据题意列出函数关系式即可求解.
【详解】解:设平均每次降价的百分率是x,,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为,
故选:D.
【点睛】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.
5.B
【详解】解:如图,建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,
则O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA和OB为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,把A点坐标(﹣2,0)代入得a=﹣0.5,
∴抛物线解析式为y=﹣0.5x2+2,
当水面下降2.5米,
把y=﹣2.5代入抛物线解析式得出:﹣2.5=﹣0.5x2+2,
解得:x=±3,
2×3﹣4=2,
所以水面下降2.5m,水面宽度增加2米,
故选B.
6.B
【分析】根据抛物线在坐标系中的位置可得B(-8,0),C(0,2),可以设抛物线的解析式为y=ax2+2,再由条件求出a的值即可;
【详解】解:根据题意得A(-8,-6),B(-8,0),C(0,2),
设抛物线的解析式为y=ax2+2(a≠0),把B(-8,0)代入
64a+2=0
解得:a= .
抛物线的解析式为y= x2+2.
故选:B.
【点睛】本题考查了二次函数的应用,求抛物线解析式可以使用一般式,顶点式或者交点式,因条件而定.
7.B
【分析】利用长方形的面积公式,可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题.
【详解】解:根据题意得:,
,
.
,且,
当时,随的增大而增大,
当时,可以取得最小整数,此时.
故选:B.
【点睛】本题考查了二次函数的性质以及二次函数的最值,根据各数量之间的关系,找出k关于a的函数关系式是解题的关键.
8.D
【分析】将C点坐标代入抛物线解析式求出a即可判断①;根据a即可得抛物线解析式,则其对称轴可得,②即可判断;只有当P点在对称轴且A、P、C三点共线时,有PB+PC最小值,连接AC交对称轴与点P,连接BP,对称轴交x轴于M点,根据轴,OA=OC=3,即有则n可求,③即可判断;连接PC、AC、OP、PA,根据可得,则④可判断.
【详解】∵抛物线过C点(0,3),
∴,
∴a=-1,即①正确,
即抛物线解析式为,
∴抛物线对称轴为,即②正确,
当x=0时,y=3,即C点坐标为(0,3)
∴OC=3,
当y=0,有,
解得x为1或者-3,
∴A(-3,0),B(1,0),
∴OA=3,OB=1,
∵B(1,0),C(0,3),
∴,
∴要求△PBC周长最小值,即求PC+PB+BC的最小值,
∵BC为定值,
∴即求PC+PB的最小值,
可知只有当P点在对称轴且A、P、C三点共线时,有PB+PC最小值,
连接AC交对称轴与点P,连接BP,对称轴交x轴于M点,如图1所示,
∵A、B关于PM对称,
∴PA=PB,
∴PB+PC=PA+PC=AC,
∵对称轴x=-1,
∴OM=1,
∴AM=OA-OM=3-1=2,
显然有轴,
有∵OA=OC=3,
∴,
∴PM=AM=2,
∴P点坐标为(-1,2),
∴n=2,
∴即△PBC周长最小值时,n=2,即③错误,
如图2所示,连接PC、AC、OP、PA,
由图有:,
∵,,,
∴,
∵P在抛物线上,
∴,
∴,
整理得:,
即当时,△PAC的面积最大,即④正确,
综上分析可得,正确的有:①②④.
故选:D.
【点睛】本题考查了二次函数的图像与性质,考查了二次函数的对称轴、最值、与坐标轴交点等知识,判断只有当P点在对称轴且A、P、C三点共线时,有PB+PC最小值,是解答本题的关键.
9.B
【分析】本题主要考查了一次函数及二次函数与几何动点问题的综合运用.熟练掌握动点产生的三角形面积计算方法,是解题关键.
根据题意,当Q点分别在、上运动时,形成了不同情况下的三角形,据此进一步用x将相对应的情况下的三角形的面积表示出来,最后观察解析式即可.
【详解】正方形的边长为,点P的速度为,点Q的速度为,P,Q两点同时出发,运动的时间为,
①当时,如下图,
,,
∴,
∵的面积为,
∴,
是开口向下顶点为的抛物线,
∴B、D符合;
②当时,如下图,
,
是y随x增大而减小的线段,
∴只有B符合.
故选:B.
10.D
【分析】点D关于AC的对称点是点B,连接EB,交AC于点P,再得出EB即为EP+DP最短,解答即可.
【详解】解:连接,如图,
点关于的对称点是点,
,
即为最的小值,
即此时周长最小,
连接交于,过作于,
四边形是菱形,
,,
,
,
,
,,
轴,
直线与轴间的距离是1,
点的纵坐标为,
,
直线的解析式为:,
,,
直线的解析式为:,
解得:,
,.
故选:D.
【点睛】此题主要考查了轴对称—最短距离问题,菱形的性质,解题关键是根据一次函数与方程组的关系,得出直线的解析式,求出交点坐标.
11.
【分析】本题主要考查了求二次函数解析式,考查学生分析解决问题的能力,属于基础题.根据平均每月增长率为x,可求二月、三月的营业额,再根据一月、二月、三月的营业额共y万元列出函数解析式即可.
【详解】解:由题意,二月的营业额为,三月的营业额为,
∵一月、二月、三月的营业额共y万元,
∴.
故答案为:.
12.4
【分析】根据抛物线的平移规律:上加下减,左加右减解答即可.
【详解】解:∵抛物线的顶点坐标为(1, -2),
先向左平移2个单位长度,再向上平移个单位长度
则平移后抛物线的顶点坐标为
平移后的抛物线解析式为,
平移后的抛物线经过点,
解得.
故答案为:4.
【点睛】本题考查了抛物线的平移规律.关键是确定平移前后抛物线的顶点坐标,寻找平移规律.
13.10
【分析】由题意得的顶点坐标是(4,3),可求出b的值,再将(4,3)代入,求得c的值,得出抛物线的关系式,最后令y=0,求出x的值即可.
【详解】解:∵实心球在运动过程中最高离地面3米,此时与运动员的水平距离为4米,
∴的顶点坐标是(4,3),
∴,
解得:,
∴抛物线关系式为
将(4,3)代入得:
解得:,
所以抛物线的解析式为.
令y=0,可得,
解得(舍去).
∴OA的长是10米.
故答案为:10.
【点睛】此题考查的是二次函数的应用,利用待定系数法得到函数解析式是解决此题的关键.
14.(-2,3)或(,-3)或(,-3)
【分析】由二次函数,令,则,可求得,令,即有,可求得,结合三角形面积公式,求解,然后根据题意可知P点的纵坐标为,分别代入函数解析式即可求得P点横坐标,进而确定P点坐标.
【详解】解:∵,
令,则,
∴,
令,即有,
解得,
由图像可知,,
∴,
∵,
∴,
解得或(不合题意,舍去),
∴该二次函数解析式为,,
∵,
∴P点的纵坐标为,
将代入,即有,
解得或(与点C重合,舍去),
将代入,即有,
解得或,
∴点P坐标为(-2,3)或(,-3)或(,-3).
故答案为:(-2,3)或(,-3)或(,-3).
【点睛】本题主要考查了抛物线与x轴交点、二次函数图像上的点的坐标特征、二次函数的图像与性质等知识,求得抛物线与坐标轴的交点坐标是解题的关键.
15./
【分析】本题考查了二次函数与轴的交点、利用轴对称求最短路线、勾股定理.准确求出二次函数与轴的交点坐标,确定当最小时,点和点的位置是解题的关键.
先求出点坐标与点坐标,作点关于轴对称的点,连接交轴于点,交于,过点作轴,连接,当点与点重合,点与点重合时,为最小,最小值为线段的长,然后可在中由勾股定理求出,进而可得即可解答.
【详解】解:对于,当时,,
解得:,,
点的坐标为,
对于,当时,,
点的坐标为,
作点关于轴对称的点,则点,
连接交轴于点,交于,过点作轴,连接,
当点与点重合,点与点重合时,为最小,最小值为线段的长.
理由:当点与点不重合,点与点不重合时,根据轴对称的性质可知:,
,
即:,
,
,
即:,
当点与点重合,点与点重合时,为最小,
,,
,,,
,
在中,,,
由勾股定理可得:,
.
即的最小值为:.
故答案为:.
16.该商场销售这种空气净化器获得的最大利润是元
【分析】本题考查二次函数;根据题意,可以得到利润和售价之间的函数关系式,然后根据二次函数的性质和的取值范围,即可求得相应的最大利润.
【详解】解:设所获利润为元,
,
某月该商场这种空气净化器的售价不低于进价不高于元台,
,
,
当时,随的增大而增大,
当时,有最大值,此时,
答:该商场销售这种空气净化器获得的最大利润是元.
17.(1),
(2)人参加旅游,选择甲旅行社比较划算
【分析】(1)根据甲乙旅行社的费用的数量关系即可求解;
(2)将人数代入(1)中的两个表达式计算,再进行比较即可;
本题主要考查一次函数的运用,理解题目中的数量关系,掌握一次函数的实际运用是解题的关键.
【详解】(1)解:由题意,得,
.
(2)解:当时,
,,
∵,
∴人参加旅游,选择甲旅行社比较划算.
18.(1)符合要求,花坛的半径至少为,理由见解析
(2)为了不影响水流,小水池的半径不能超过米
【分析】(1)设二次函数顶点式,利用待定系数法求出二次函数解析式,求出抛物线与x轴的交点坐标,即可得到答案;
(2)令,则,解得或舍,即可得到答案.
【详解】(1)解:符合要求,理由如下:
由题意可得,顶点为,
设解析式为,
函数过点,
代入解析式得,,
解得,
解析式为:,
令,则,
解得或舍去,
花坛的半径至少为;
(2)令,则,
解得或舍,
为了不影响水流,小水池的半径不能超过米.
【点睛】此题考查了二次函数的实际应用,数形结合和准确计算是解题的关键.
19.(1),
(2)作图见详解,电流随可变电阻的增大而减小
(3)电子体重秤可称的最大质量为千克
【分析】本题主要考查反比例函数,一次函数图象的综合运用,掌握自变量,函数值的计算方法,待定系数法求解析是解题的关键.
(1)根据题意,分别把,代入,即可求解;
(2)根据函数图象作图的方法,列表、描点、平滑曲线连接的方法即可求解;
(3)根据题意可求出可变电阻与踏板上人的质量之间函数关系为,根据电流表量程,电流与电压,电阻的函数关系可求出子体重秤可称的最大质量.
【详解】(1)解:已知电流(单位:)与定值电阻.可变电阻(单位:)之间关系为 ,电源电压恒为, 定值电阻的阻值为,
∴当时,,即;
当时,,
解得,,即;
故答案为:,;
(2)解:根据题意,
… 1 2 3 4 6 …
4 3 2
根据表格数据在平面直角坐标系中描点如下,
∴根据图示,电流随可变电阻的增大而减小;
(3)解:根据题意,设可变电阻与人的质量的函数关系为,且该直线过,,
∴,
解得,,
∴可变电阻与人的质量的函数关系为:,
∴可变电阻随人的质量增大而减小,
当时,,
∴;
当时,,
∴;
∵,
∴不能超过;
当时,,
解得,,
∴,
解得,,
∴电子体重秤可称的最大质量为千克.
20.(1)
(2)点M的坐标为,,
【分析】(1)利用对称性可得,则利用交点式得抛物线解析式为,所以,解得,于是得到抛物线解析式为;
(2)分类讨论:当时,易得点,如图;②当时,先计算出,再以点为圆心,为半径画弧交轴于,,如图,易得.
【详解】(1)解:(1)∵点和点B关于直线对称,
∴,
∴抛物线解析式为:,
∴,解得,
∴抛物线解析式为;
(2)当时,点与点C关于轴对称,则,如图;
②当时,,
以点为圆心,为半径画弧交轴于,,如图,则,,则,,
综上所述,满足条件的点M的坐标为,,.
【点睛】本题考查了抛物线与x轴的交点:把求二次函数(是常数,)与x轴的交点坐标问题转化为解关于的一元二次方程.解决(2)小题的关键是利用等腰三角形的性质画出点的坐标.
21.(1)
(2)元
(3)9元
【分析】(1)由待定系数法即可得到函数的解析式;
(2)根据(1)的解析式将x=3代入求出销售量,再根据每千克利润×销售量=总利润列式求解即可;
(3)根据这种干果每千克的利润×销售量=2090列出方程,解方程即可.
【详解】(1)解:设y与x之间的函数关系式为:y=kx+b,
把(2,120)和(4,140)代入得,,
解得:,
∴y与x之间的函数关系式为:y=10x+100(0<x<20);
(2)解:根据题意得,x=3时销售量,
(元),
答:当每千克干果降价元时,超市获利元;
(3)解:根据题意得,(60-x-40)(10x+100)=2090;
解得:x1=1,x2=9;整理得:x2-10x+9=0
为了让顾客获得更大实惠,x=9
答:这种干果每千克应降价9元.
【点睛】本题考查了一元二次方程的应用和一次函数的应用,读懂图象信息、熟练掌握待定系数法、正确列出一元二次方程是解题的关键.
22.(1),
(2)与的函数关系式是:
【分析】(1)求出,根据直角三角形性质求出,由角平分线的性质可得,进而得到,,在中,根据勾股定理得出关于的方程,求出即可;
(2)有两种情况:①当在上,在上时,,过作,交的延长线于,求出,再根据三角形的面积公式求解即可;②当在上,Q在上时,,过作于,过作于,求出和的值,最后根据 即可求解.
【详解】(1)解:中,,,
,
,
平分,
,
,,
在中,,即,
解得:,
,
,;
(2)①当在上,在上时,,
则,,
过作,交的延长线于,
,
,
,,
,即;
②当在上,Q在上时,,
过作于,过作于,
,,
,,,,
,
,
即,
综合上述:与的函数关系式是:.
【点睛】本题考查了等腰三角形的性质,三角形的面积,图形的动点问题与二次函数,勾股定理,含的直角三角形性质等知识点的运用,运用分类讨论思想是解题的关键.
23.(1)A;(2)见解析;(3)①见解析;②
【分析】(1)根据和谐四边形的定义进行判断即可;
(2)过点作于点,过点作于点,根据,得到,证明,即可得证;
(3)①在上取一点T,使得,连接,证明四边形是平行四边形,进而得到,得到,推出,得到,再利用外角的性质,可得结论.
②联立直线和抛物线的解析式,求出两点坐标,过点作轴,过点作,过点作,证明,求出点坐标,分和,两种情况讨论求解即可.
【详解】解:(1)只有平行四边形的对角线把平分四边形的面积分成两个面积相等的三角形,
故选A;
(2)证明:过点作于点,过点作于点,
则:,
∵,
∴,
又∵,
∴,
∴;
(3)①证明:如图2中,在上取一点T,使得,连接.
∵四边形是和谐四边形,是和谐对角线,
由(2)可知:,
又∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴.
②联立,解得:或;
∴,
过点作轴,过点作,过点作,则:,,
∵,
∴,
∴,
∴,
∴,
∴,
∵四边形是和谐四边形,
∴或,
当时,
∵直线的解析式为:,设直线于轴的交点为
∴当时,,
∴直线与轴的交点坐标为,
∴,
∴将直线向上平移5个单位,得到,
联立,解得:或,
∵点在第一象限,
∴点的横坐标为;
当时,则为和谐对角线,
由(2)可知,的中点在直线上,
∵,
∴的中点坐标为,
设直线的解析式为:,把代入,得:,
∴,
此时直线与抛物线的交点在二,四象限,不符合题意;
综上:点的横坐标为.
【点睛】本题主要考查了平行四边形的判定和性质,和谐四边形的定义,全等三角形的判定和性质,等腰三角形的判定和性质,三角形的外角,二次函数的综合应用等知识,解题的关键是掌握和谐四边形的定义,学会添加常用辅助线,构造全等三角形进和特殊四边形解决问题.
21世纪教育网(www.21cnjy.com)
拔高提升同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.关于二次函数,下列说法正确的是( )
A.图象与y轴的交点坐标为 B.图象的对称轴在y轴的左侧
C.图象与x轴没有交点 D.y的最大值为4
2.一个运动员打高尔夫球,若球的飞行高度y(m)与水平距离x(m)之间的函数表达式为:y(x﹣25)2+12,则高尔夫球在飞行过程中的最大高度为( )m.
A.12 B.25 C.13 D.14
3.烟花厂某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣2t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.10s
4.进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为( )
A. B. C. D.
5.如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )
A.1 m B.2 m C.3 m D.6 m
6.如图,隧道的截面由抛物线和长方形构成.长方形的长为,宽为,抛物线的最高点离路面的距离为.在如图所示的直角坐标系中,该抛物线的函数表达式可表示为( )
A. B. C. D.
7.如图1,一张边长为、(为正整数)的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
8.如图,抛物线经过点,点从点A出发,沿抛物线运动到顶点后,再沿对称轴l向下运动,给出下列说法:
①a=-1;
②抛物线的对称轴为x=-1;
③当点P,B,C构成的三角形的周长取最小值时,n=1;
④在点P从点A运动到顶点的过程中,当时,△PAC的面积最大.
其中,所有正确的说法是( )
A.①③ B.②③④ C.①④ D.①②④
9.如图,正方形的边长为,点P以的速度从点A出发沿着方向运动到点B停止,点Q以的速度沿运动到点D停止,P,Q两点同时出发,设运动的时间为,的面积为,则y关于x的函数图象大致是( )
A. B. C. D.
10.已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4,点P是对角线AC上的一个动点,E(0,2),当周长最小时,点P的坐标为( ).
A.(2,2) B.(2,) C.(,) D.(,)
二、填空题
11.某超市一月份的营业额为200万元,一月、二月、三月的营业额共y万元,如果平均每月增长率为x,则营业额y与月平均增长率x之间的函数关系式为 .
12.将抛物线先向左平移2个单位长度,再向上平移个单位长度.若得到的抛物线经过点,则的值是 .
13.实心球是一项以力量为基础,以动作速度为核心的投掷项目.如图,某次比赛中运动员站在O处将实心球从B处抛出,它的运动路线可以看作是抛物线的一部分.若实心球在运动过程中最高离地面3米,此时与运动员的水平距离为4米,则该运动员投掷实心球的水平距离OA为 米.
14.如图,已知二次函数的图像与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知的面积是6,若在抛物线上存在一点P(与点C不重合),使,则点P的坐标为 .
15.如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.若点D为抛物线上一点且横坐标为,点E为y轴上一点,点F在以点A为圆心,2为半径的圆上,则的最小值 .
三、解答题
16.冬季天气干燥,空气加湿器得以畅销,某商场销售一种空气加湿器,进价是每台元,月销售量(台)与售价(元台)满足一次函数关系式.若某月规定该商场的这种空气加湿器的售价不低于进价且不高于元台,则该商场该月销售这种空气加湿器获得的最大利润是多少元?
17.某中学组织开展“回顾党史,重温初心”的红色研学旅行,估计人数在之间.甲、乙两家旅行社原价均为元/人,甲旅行社优惠方案:所有人八折优惠;乙旅行社优惠方案:人以内(含人)按原价收费,超过的人数每人费用降低.
(1)分别写出两家旅行社旅行费用(元)与人数之间的函数关系式;
(2)若有人参加旅游,选择哪家旅行社比较划算?
18.阅读以下材料,完成课题研究任务:
【研究课题】设计公园喷水池
【素材】某公园计划修建一个图所示的喷水池,水池中心处立着一个高为的实心石柱,水池周围安装一圈喷头,使得水流在各个方向上都沿形状相同的抛物线喷出,并在石柱顶点处汇合为使水流形状更漂亮,要求水流在距离石柱处能达到最大高度,且离池面的高度为.
【素材】距离池面米的位置,围绕石柱还修了一个小水池,要求小水池不能影响水流.
【任务解决】
(1)小张同学设计的水池半径为,请你结合已学知识,判断他设计的水池是否符合要求.
(2)为了不影响水流,小水池的半径不能超过多少米?
19.某数学活动小组研究一款如图①简易电子体重秤,当人踏上体重秤的踏板后,读数器可以显示人的质量(单位:).图②是该秤的电路图,已知串联电路中,电流(单位:)与定值电阻.可变电阻(单位:)之间关系为 ,电源电压恒为, 定值电阻的阻值为.
根据与之间的关系得出一组数据如下:
… 1 2 3 q 6 …
4 p 2
(1)填空: , ;
(2)该小组把上述问题抽象为数学模型,请根据表中数据在图③中描出实数对的对应点,画出函数 的图象,并写出一条此函数图象关于增减性的性质.
(3)若电流表量程是,可变电阻与踏板上人的质量之间函数关系如图④所示,为保护电流表,求电子体重秤可称的最大质量为多少千克?
20.如图,已知抛物线与轴的一个交点为,另一个交点为,与轴的交点为,其顶点为,对称轴为直线.
(1)求抛物线的解析式;
(2)已知点为轴上的一个动点,当是以为一腰的等腰三角形时,求点M的坐标.
21.某超市以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)之间满足一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)当每千克干果降价3元时,超市获利多少元?
(3)若超市要想获利2090元,且让顾客获得更大实惠,这种干果每千克应降价多少元?
22.如图(1)中,,,,的平分线交于,过点作与垂直的直线.动点从点出发沿折线以每秒个单位长度的速度向终点运动,运动时间为秒,同时动点从点出发沿折线以相同的速度运动,当点到达点时、同时停止运动.
(1)求、的长;
(2)设的面积为,求与的函数关系式,并求出自变量的取值范围.
23.定义:如果四边形的一条对角线把这个四边形分成面积相等的两个三角形,那么这个四边形叫做和谐四边形,这条对角线叫做和谐对角线,
[概念理解]
(1)下列图形中,属于和谐四边形的是____________.
A.平行四边形 B.对角线互相垂直的四边形 C.对角线相等的四边形
[性质探讨];
(2)和谐四边形的性质:在和谐四边形中,和谐对角线平分另一条对角线.利用所学知识证明和谐四边形的性质,即:
如图1,已知:四边形是和谐四边形,和谐对角线与对角线交于点与的面积相等.求证:.
[探究应用];
(3)①如图2,已知四边形是和谐四边形,和谐对角线与对角线交于点.求证:;
②如图3,已知直线与抛物线交于两点,点在轴负半轴上,满足,点在第一象限且位于抛物线上,若四边形是和谐四边形,求点的横坐标.
21世纪教育网(www.21cnjy.com)
1.D
【分析】根据二次函数的性质及与坐标轴的交点问题依次判断即可.
【详解】解:A、∵二次函数,
当时,,
∴与y轴交点坐标为,选项说法错误,不符合题意;
B、
∵对称轴为,
∴对称轴在y轴右侧,选项说法错误,不符合题意;
C、当时,,
,
∴图象与x轴有两个交点,选项说法错误,不符合题意;
D、∵,有最大值,
当时,,
∴顶点坐标为,y有最大值4,选项说法正确,符合题意;
故选:D.
【点睛】本题主要考查了二次函数的性质,解答本题的关键是熟练掌握二次函数图象的顶点坐标,对称轴以及开口方向等,此题难度不大.
2.A
【分析】直接根据二次函数的图象及性质即可得出答案.
【详解】解:∵y(x﹣25)2+12,
顶点坐标为(25,12),
∵0,
∴当x=25时,y有最大值,最大值为12.
故选:A.
【点睛】本题主要考查二次函数的最大值,掌握二次函数的图象和性质是解题的关键.
3.C
【分析】将h关于t的函数关系式变形为顶点式,即可得出升到最高点的时间,从而得出结论.
【详解】解:∵h=﹣2t2+20t+1=﹣2(t﹣5)2+51,
∴当t=5时,礼炮升到最高点.
故选:C.
【点睛】本题考查了二次函数的应用,解题的关键是将二次函数的关系式变形为顶点式.本题属于基础题,难度不大,解决该题型题目时,将函数的关系式进行变换找出顶点坐标即可.
4.D
【分析】设平均每次降价的百分率是x,,第一次降价后的价格为,第二次降价的价格为,根据题意列出函数关系式即可求解.
【详解】解:设平均每次降价的百分率是x,,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为,
故选:D.
【点睛】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.
5.B
【详解】解:如图,建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,
则O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA和OB为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,把A点坐标(﹣2,0)代入得a=﹣0.5,
∴抛物线解析式为y=﹣0.5x2+2,
当水面下降2.5米,
把y=﹣2.5代入抛物线解析式得出:﹣2.5=﹣0.5x2+2,
解得:x=±3,
2×3﹣4=2,
所以水面下降2.5m,水面宽度增加2米,
故选B.
6.B
【分析】根据抛物线在坐标系中的位置可得B(-8,0),C(0,2),可以设抛物线的解析式为y=ax2+2,再由条件求出a的值即可;
【详解】解:根据题意得A(-8,-6),B(-8,0),C(0,2),
设抛物线的解析式为y=ax2+2(a≠0),把B(-8,0)代入
64a+2=0
解得:a= .
抛物线的解析式为y= x2+2.
故选:B.
【点睛】本题考查了二次函数的应用,求抛物线解析式可以使用一般式,顶点式或者交点式,因条件而定.
7.B
【分析】利用长方形的面积公式,可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题.
【详解】解:根据题意得:,
,
.
,且,
当时,随的增大而增大,
当时,可以取得最小整数,此时.
故选:B.
【点睛】本题考查了二次函数的性质以及二次函数的最值,根据各数量之间的关系,找出k关于a的函数关系式是解题的关键.
8.D
【分析】将C点坐标代入抛物线解析式求出a即可判断①;根据a即可得抛物线解析式,则其对称轴可得,②即可判断;只有当P点在对称轴且A、P、C三点共线时,有PB+PC最小值,连接AC交对称轴与点P,连接BP,对称轴交x轴于M点,根据轴,OA=OC=3,即有则n可求,③即可判断;连接PC、AC、OP、PA,根据可得,则④可判断.
【详解】∵抛物线过C点(0,3),
∴,
∴a=-1,即①正确,
即抛物线解析式为,
∴抛物线对称轴为,即②正确,
当x=0时,y=3,即C点坐标为(0,3)
∴OC=3,
当y=0,有,
解得x为1或者-3,
∴A(-3,0),B(1,0),
∴OA=3,OB=1,
∵B(1,0),C(0,3),
∴,
∴要求△PBC周长最小值,即求PC+PB+BC的最小值,
∵BC为定值,
∴即求PC+PB的最小值,
可知只有当P点在对称轴且A、P、C三点共线时,有PB+PC最小值,
连接AC交对称轴与点P,连接BP,对称轴交x轴于M点,如图1所示,
∵A、B关于PM对称,
∴PA=PB,
∴PB+PC=PA+PC=AC,
∵对称轴x=-1,
∴OM=1,
∴AM=OA-OM=3-1=2,
显然有轴,
有∵OA=OC=3,
∴,
∴PM=AM=2,
∴P点坐标为(-1,2),
∴n=2,
∴即△PBC周长最小值时,n=2,即③错误,
如图2所示,连接PC、AC、OP、PA,
由图有:,
∵,,,
∴,
∵P在抛物线上,
∴,
∴,
整理得:,
即当时,△PAC的面积最大,即④正确,
综上分析可得,正确的有:①②④.
故选:D.
【点睛】本题考查了二次函数的图像与性质,考查了二次函数的对称轴、最值、与坐标轴交点等知识,判断只有当P点在对称轴且A、P、C三点共线时,有PB+PC最小值,是解答本题的关键.
9.B
【分析】本题主要考查了一次函数及二次函数与几何动点问题的综合运用.熟练掌握动点产生的三角形面积计算方法,是解题关键.
根据题意,当Q点分别在、上运动时,形成了不同情况下的三角形,据此进一步用x将相对应的情况下的三角形的面积表示出来,最后观察解析式即可.
【详解】正方形的边长为,点P的速度为,点Q的速度为,P,Q两点同时出发,运动的时间为,
①当时,如下图,
,,
∴,
∵的面积为,
∴,
是开口向下顶点为的抛物线,
∴B、D符合;
②当时,如下图,
,
是y随x增大而减小的线段,
∴只有B符合.
故选:B.
10.D
【分析】点D关于AC的对称点是点B,连接EB,交AC于点P,再得出EB即为EP+DP最短,解答即可.
【详解】解:连接,如图,
点关于的对称点是点,
,
即为最的小值,
即此时周长最小,
连接交于,过作于,
四边形是菱形,
,,
,
,
,
,,
轴,
直线与轴间的距离是1,
点的纵坐标为,
,
直线的解析式为:,
,,
直线的解析式为:,
解得:,
,.
故选:D.
【点睛】此题主要考查了轴对称—最短距离问题,菱形的性质,解题关键是根据一次函数与方程组的关系,得出直线的解析式,求出交点坐标.
11.
【分析】本题主要考查了求二次函数解析式,考查学生分析解决问题的能力,属于基础题.根据平均每月增长率为x,可求二月、三月的营业额,再根据一月、二月、三月的营业额共y万元列出函数解析式即可.
【详解】解:由题意,二月的营业额为,三月的营业额为,
∵一月、二月、三月的营业额共y万元,
∴.
故答案为:.
12.4
【分析】根据抛物线的平移规律:上加下减,左加右减解答即可.
【详解】解:∵抛物线的顶点坐标为(1, -2),
先向左平移2个单位长度,再向上平移个单位长度
则平移后抛物线的顶点坐标为
平移后的抛物线解析式为,
平移后的抛物线经过点,
解得.
故答案为:4.
【点睛】本题考查了抛物线的平移规律.关键是确定平移前后抛物线的顶点坐标,寻找平移规律.
13.10
【分析】由题意得的顶点坐标是(4,3),可求出b的值,再将(4,3)代入,求得c的值,得出抛物线的关系式,最后令y=0,求出x的值即可.
【详解】解:∵实心球在运动过程中最高离地面3米,此时与运动员的水平距离为4米,
∴的顶点坐标是(4,3),
∴,
解得:,
∴抛物线关系式为
将(4,3)代入得:
解得:,
所以抛物线的解析式为.
令y=0,可得,
解得(舍去).
∴OA的长是10米.
故答案为:10.
【点睛】此题考查的是二次函数的应用,利用待定系数法得到函数解析式是解决此题的关键.
14.(-2,3)或(,-3)或(,-3)
【分析】由二次函数,令,则,可求得,令,即有,可求得,结合三角形面积公式,求解,然后根据题意可知P点的纵坐标为,分别代入函数解析式即可求得P点横坐标,进而确定P点坐标.
【详解】解:∵,
令,则,
∴,
令,即有,
解得,
由图像可知,,
∴,
∵,
∴,
解得或(不合题意,舍去),
∴该二次函数解析式为,,
∵,
∴P点的纵坐标为,
将代入,即有,
解得或(与点C重合,舍去),
将代入,即有,
解得或,
∴点P坐标为(-2,3)或(,-3)或(,-3).
故答案为:(-2,3)或(,-3)或(,-3).
【点睛】本题主要考查了抛物线与x轴交点、二次函数图像上的点的坐标特征、二次函数的图像与性质等知识,求得抛物线与坐标轴的交点坐标是解题的关键.
15./
【分析】本题考查了二次函数与轴的交点、利用轴对称求最短路线、勾股定理.准确求出二次函数与轴的交点坐标,确定当最小时,点和点的位置是解题的关键.
先求出点坐标与点坐标,作点关于轴对称的点,连接交轴于点,交于,过点作轴,连接,当点与点重合,点与点重合时,为最小,最小值为线段的长,然后可在中由勾股定理求出,进而可得即可解答.
【详解】解:对于,当时,,
解得:,,
点的坐标为,
对于,当时,,
点的坐标为,
作点关于轴对称的点,则点,
连接交轴于点,交于,过点作轴,连接,
当点与点重合,点与点重合时,为最小,最小值为线段的长.
理由:当点与点不重合,点与点不重合时,根据轴对称的性质可知:,
,
即:,
,
,
即:,
当点与点重合,点与点重合时,为最小,
,,
,,,
,
在中,,,
由勾股定理可得:,
.
即的最小值为:.
故答案为:.
16.该商场销售这种空气净化器获得的最大利润是元
【分析】本题考查二次函数;根据题意,可以得到利润和售价之间的函数关系式,然后根据二次函数的性质和的取值范围,即可求得相应的最大利润.
【详解】解:设所获利润为元,
,
某月该商场这种空气净化器的售价不低于进价不高于元台,
,
,
当时,随的增大而增大,
当时,有最大值,此时,
答:该商场销售这种空气净化器获得的最大利润是元.
17.(1),
(2)人参加旅游,选择甲旅行社比较划算
【分析】(1)根据甲乙旅行社的费用的数量关系即可求解;
(2)将人数代入(1)中的两个表达式计算,再进行比较即可;
本题主要考查一次函数的运用,理解题目中的数量关系,掌握一次函数的实际运用是解题的关键.
【详解】(1)解:由题意,得,
.
(2)解:当时,
,,
∵,
∴人参加旅游,选择甲旅行社比较划算.
18.(1)符合要求,花坛的半径至少为,理由见解析
(2)为了不影响水流,小水池的半径不能超过米
【分析】(1)设二次函数顶点式,利用待定系数法求出二次函数解析式,求出抛物线与x轴的交点坐标,即可得到答案;
(2)令,则,解得或舍,即可得到答案.
【详解】(1)解:符合要求,理由如下:
由题意可得,顶点为,
设解析式为,
函数过点,
代入解析式得,,
解得,
解析式为:,
令,则,
解得或舍去,
花坛的半径至少为;
(2)令,则,
解得或舍,
为了不影响水流,小水池的半径不能超过米.
【点睛】此题考查了二次函数的实际应用,数形结合和准确计算是解题的关键.
19.(1),
(2)作图见详解,电流随可变电阻的增大而减小
(3)电子体重秤可称的最大质量为千克
【分析】本题主要考查反比例函数,一次函数图象的综合运用,掌握自变量,函数值的计算方法,待定系数法求解析是解题的关键.
(1)根据题意,分别把,代入,即可求解;
(2)根据函数图象作图的方法,列表、描点、平滑曲线连接的方法即可求解;
(3)根据题意可求出可变电阻与踏板上人的质量之间函数关系为,根据电流表量程,电流与电压,电阻的函数关系可求出子体重秤可称的最大质量.
【详解】(1)解:已知电流(单位:)与定值电阻.可变电阻(单位:)之间关系为 ,电源电压恒为, 定值电阻的阻值为,
∴当时,,即;
当时,,
解得,,即;
故答案为:,;
(2)解:根据题意,
… 1 2 3 4 6 …
4 3 2
根据表格数据在平面直角坐标系中描点如下,
∴根据图示,电流随可变电阻的增大而减小;
(3)解:根据题意,设可变电阻与人的质量的函数关系为,且该直线过,,
∴,
解得,,
∴可变电阻与人的质量的函数关系为:,
∴可变电阻随人的质量增大而减小,
当时,,
∴;
当时,,
∴;
∵,
∴不能超过;
当时,,
解得,,
∴,
解得,,
∴电子体重秤可称的最大质量为千克.
20.(1)
(2)点M的坐标为,,
【分析】(1)利用对称性可得,则利用交点式得抛物线解析式为,所以,解得,于是得到抛物线解析式为;
(2)分类讨论:当时,易得点,如图;②当时,先计算出,再以点为圆心,为半径画弧交轴于,,如图,易得.
【详解】(1)解:(1)∵点和点B关于直线对称,
∴,
∴抛物线解析式为:,
∴,解得,
∴抛物线解析式为;
(2)当时,点与点C关于轴对称,则,如图;
②当时,,
以点为圆心,为半径画弧交轴于,,如图,则,,则,,
综上所述,满足条件的点M的坐标为,,.
【点睛】本题考查了抛物线与x轴的交点:把求二次函数(是常数,)与x轴的交点坐标问题转化为解关于的一元二次方程.解决(2)小题的关键是利用等腰三角形的性质画出点的坐标.
21.(1)
(2)元
(3)9元
【分析】(1)由待定系数法即可得到函数的解析式;
(2)根据(1)的解析式将x=3代入求出销售量,再根据每千克利润×销售量=总利润列式求解即可;
(3)根据这种干果每千克的利润×销售量=2090列出方程,解方程即可.
【详解】(1)解:设y与x之间的函数关系式为:y=kx+b,
把(2,120)和(4,140)代入得,,
解得:,
∴y与x之间的函数关系式为:y=10x+100(0<x<20);
(2)解:根据题意得,x=3时销售量,
(元),
答:当每千克干果降价元时,超市获利元;
(3)解:根据题意得,(60-x-40)(10x+100)=2090;
解得:x1=1,x2=9;整理得:x2-10x+9=0
为了让顾客获得更大实惠,x=9
答:这种干果每千克应降价9元.
【点睛】本题考查了一元二次方程的应用和一次函数的应用,读懂图象信息、熟练掌握待定系数法、正确列出一元二次方程是解题的关键.
22.(1),
(2)与的函数关系式是:
【分析】(1)求出,根据直角三角形性质求出,由角平分线的性质可得,进而得到,,在中,根据勾股定理得出关于的方程,求出即可;
(2)有两种情况:①当在上,在上时,,过作,交的延长线于,求出,再根据三角形的面积公式求解即可;②当在上,Q在上时,,过作于,过作于,求出和的值,最后根据 即可求解.
【详解】(1)解:中,,,
,
,
平分,
,
,,
在中,,即,
解得:,
,
,;
(2)①当在上,在上时,,
则,,
过作,交的延长线于,
,
,
,,
,即;
②当在上,Q在上时,,
过作于,过作于,
,,
,,,,
,
,
即,
综合上述:与的函数关系式是:.
【点睛】本题考查了等腰三角形的性质,三角形的面积,图形的动点问题与二次函数,勾股定理,含的直角三角形性质等知识点的运用,运用分类讨论思想是解题的关键.
23.(1)A;(2)见解析;(3)①见解析;②
【分析】(1)根据和谐四边形的定义进行判断即可;
(2)过点作于点,过点作于点,根据,得到,证明,即可得证;
(3)①在上取一点T,使得,连接,证明四边形是平行四边形,进而得到,得到,推出,得到,再利用外角的性质,可得结论.
②联立直线和抛物线的解析式,求出两点坐标,过点作轴,过点作,过点作,证明,求出点坐标,分和,两种情况讨论求解即可.
【详解】解:(1)只有平行四边形的对角线把平分四边形的面积分成两个面积相等的三角形,
故选A;
(2)证明:过点作于点,过点作于点,
则:,
∵,
∴,
又∵,
∴,
∴;
(3)①证明:如图2中,在上取一点T,使得,连接.
∵四边形是和谐四边形,是和谐对角线,
由(2)可知:,
又∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴.
②联立,解得:或;
∴,
过点作轴,过点作,过点作,则:,,
∵,
∴,
∴,
∴,
∴,
∴,
∵四边形是和谐四边形,
∴或,
当时,
∵直线的解析式为:,设直线于轴的交点为
∴当时,,
∴直线与轴的交点坐标为,
∴,
∴将直线向上平移5个单位,得到,
联立,解得:或,
∵点在第一象限,
∴点的横坐标为;
当时,则为和谐对角线,
由(2)可知,的中点在直线上,
∵,
∴的中点坐标为,
设直线的解析式为:,把代入,得:,
∴,
此时直线与抛物线的交点在二,四象限,不符合题意;
综上:点的横坐标为.
【点睛】本题主要考查了平行四边形的判定和性质,和谐四边形的定义,全等三角形的判定和性质,等腰三角形的判定和性质,三角形的外角,二次函数的综合应用等知识,解题的关键是掌握和谐四边形的定义,学会添加常用辅助线,构造全等三角形进和特殊四边形解决问题.
21世纪教育网(www.21cnjy.com)
同课章节目录
