人教版2024-2025学年九年级数学上册23.1图形的旋转拔高提升同步练习(附答案解析)
文档属性
| 名称 | 人教版2024-2025学年九年级数学上册23.1图形的旋转拔高提升同步练习(附答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-27 21:39:09 | ||
图片预览



文档简介
人教版2024-2025学年九年级数学上册23.1图形的旋转拔高提升同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.经过下列变换,能由图①所示的基本图形得到图②的是( )
A.旋转 B.中心对称和轴对称
C.平移和轴对称 D.中心对称
2.如图,绕点O逆时针旋转,得到,若,则等于( )
A. B. C. D.
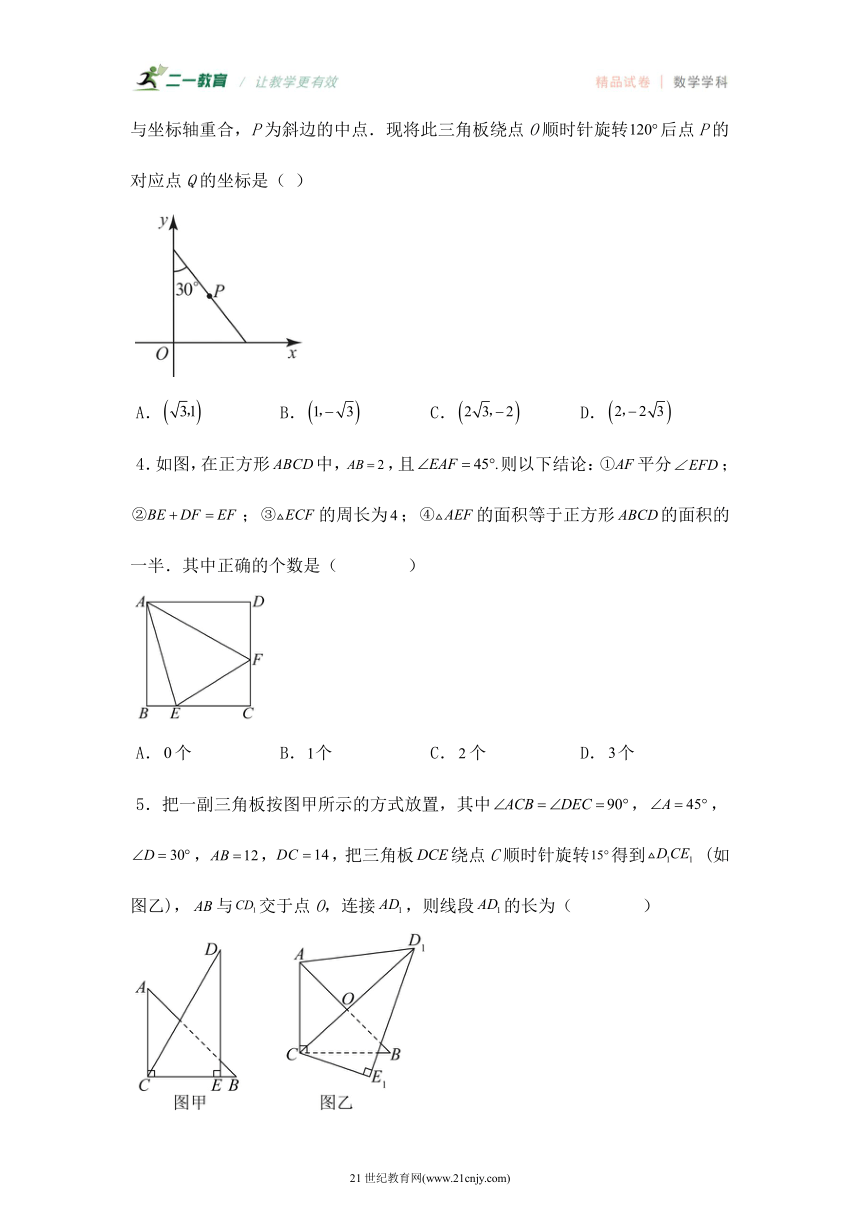
3.如图,将斜边长为4的直角三角板放在直角坐标系中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转后点P的对应点Q的坐标是( )
A. B. C. D.
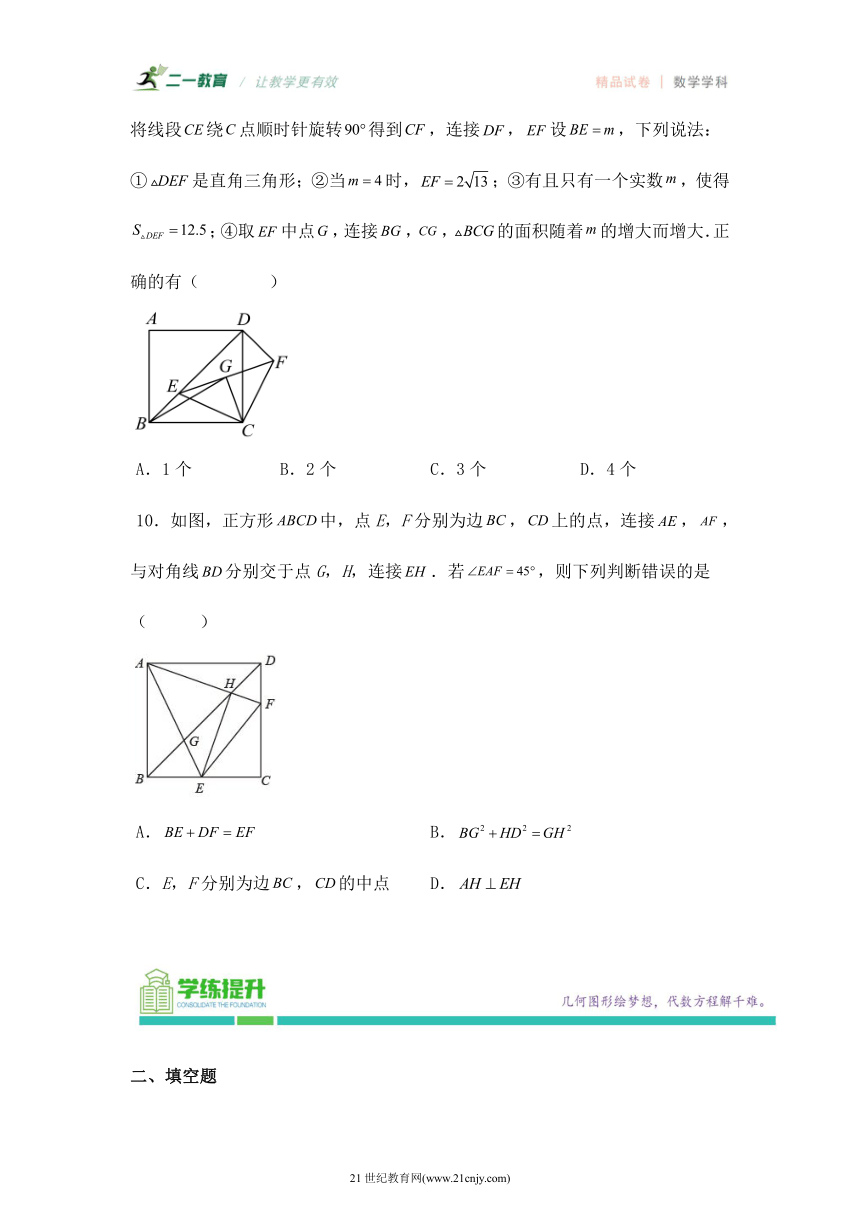
4.如图,在正方形中,,且则以下结论:平分;;的周长为;的面积等于正方形的面积的一半.其中正确的个数是( )
A.个 B.个 C.个 D.个
5.把一副三角板按图甲所示的方式放置,其中,,,,,把三角板绕点C顺时针旋转得到 (如图乙),与交于点O,连接,则线段的长为( )
A.6 B.10 C.8 D.
6.如图,将绕点顺时针旋转,点的对应点为点,点的对应点为点,当旋转角为,,,三点在同一直线上时,则的度数为( )
A. B. C. D.
7.如图,在中,,,.将绕点旋 得,分别取,的中点,,则的取值范围是( )
A. B. C. D.
8.如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
9.如图,正方形边长为,从出发沿对角线向运动,连接,将线段绕点顺时针旋转得到,连接,设,下列说法:①是直角三角形;②当时,;③有且只有一个实数,使得;④取中点,连接,,的面积随着的增大而增大.正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形中,点E,F分别为边,上的点,连接,,与对角线分别交于点G,H,连接.若,则下列判断错误的是( )
A. B.
C.E,F分别为边,的中点 D.
二、填空题
11.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为6,中心为O,在正方形外有一点P,,当正方形绕着点O旋转时,则点P到正方形的最短距离d的最大值为 .
12.将三角形 绕顶点O旋转到如图所示的位置,若,,则 .
13.如图,在,将在平面内绕点A逆时针旋转到的位置,连接.若,则旋转角的度数为 °.
14.如图,已知是等腰直角三角形,,将线段AC绕点A逆时针旋转得到,连接,.当是等腰三角形(不含等腰直角三角形)时, .
15.如图,在中,,点P为上一点,将线段绕点P顺时针旋转得线段,点Q在射线上,当的垂直平分线经过一边中点时,的长为 .
三、解答题
16.如图,一块四边形的土地,其中,,,,.
(1)试说明;
(2)求这块土地的面积.
17.在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)把平移后,点A移到点,,画出平移后得到的,并写出、的坐标;
(2)把绕点按逆时针方向旋转90°,画出旋转后的,并写出B2、C2的坐标.
18.如图,在平面直角坐标系中,的位置如图所示,每个小正方形边长为单位1,的三个顶点分别在正方形格点上.
(1)请画出关于x轴对称的图形;
(2)直接写出的面积.
19.在平面直角坐标系中,的位置如图所示,且点,.
(1)画出绕点O顺时针旋转后得到的;
(2)直接写出点A的对称点的坐标.
20.如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点).
(1)将向下平移3个单位长度,再向右平移2个单位长度,得到,请画出;
(2)已知点M为的中点,以点M为旋转中心,将线段顺时针旋转,得到线段,请画出线段.
21.如图1,在△ACB和△AED中,AC=BC,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=6,BE=8,求EF的长;
(2)求证:CE=EF;
(3)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立?并说明理由.
22.如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
(1)请画出旋转中心G (保留画图痕迹),并连接GF,GE;
(2)若正方形的边长为2a,当CE= 时,S△FGE=S△FBE;当CE= 时,S△FGE=3S△FBE.
23.在四边形ABCD中,∠DAB+∠DCB=180°,AC平分∠DAB.
(1)如图1,求证:BC=CD;
(2)如图2,连接BD交AC于点E,若∠ADB=90°,AE=2DE,求∠ABD的度数;
(3)如图3,在(2)的条件下,过点C作CH⊥AB于点H,△BCH沿BC翻折,点H的对应点为点F,点G在线段AB上,连接FG,若∠CGF=30°,S△CHG=9,求线段CG的长.
21世纪教育网(www.21cnjy.com)
1.A
【分析】根据旋转,中心对称,轴对称和平移的性质求解即可.
【详解】A中,经过旋转能由基本图形得到题图②,故该选项符合题意;
B中,经过中心对称和轴对称不能由基本图形得到题图②,故该选项不符合题意;
C中,经过平移和轴对称不能由基本图形得到题图②,故该选项不符合题意;
D中,只经过中心对称不能由基本图形得到题图②,故该选项符合题意,
故选:A.
【点睛】此题考查了旋转,中心对称,轴对称和平移的性质,解题的关键是熟练掌握旋转,中心对称,轴对称和平移的性质.旋转的特性∶不改变图形的形状和大小;经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.对应角相等,对应线段也相等.平移的特性∶平移只改变图形的位置,不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等.轴对称图形的特性∶关于某直线对称的两个图形是全等的;图形的对应点连线段被同一条直线垂直平分;对应线段或延长线与对称轴交于一点.
2.C
【分析】本题考查了旋转的性质,确定旋转角以及旋转前后对应角相等是解题关键.
【详解】解:由题意得:,,
∴,
故选:C
3.B
【分析】如图所示,连接,过Q作轴,由旋转的性质可得,由直角三角形斜边上的中线等于斜边的一半得到,则,进而推出,,由旋转的性质得到,则,再分别求出的长即可得到答案.
【详解】解:如图所示,连接,过Q作轴,
由旋转的性质可得,
∵,P为斜边的中点.
∴,
∴,
∴,
∴,
∴,
∴
在中,,
∴,,
∴P的对应点Q的坐标为,
故选B.
【点睛】本题主要考查了坐标与图形变化——旋转,含30度角的直角三角形的性质,勾股定理,直角三角形斜边上的中线,等腰三角形的性质与判定等等,灵活运用所学知识是解题的关键.
4.D
【分析】将绕点顺时针旋转得,然后证明≌,再逐一判断即可.
【详解】如图,将绕点顺时针旋转得到.
根据旋转的性质,得
,,,,.
①∵,
∴.
∴.
在和中,
∴,
∴.
∴.
∴平分.
故①正确.
②∵,
∴,
故②正确.
③.
故③正确.
④∵,
∴.
∵的长度不固定,
∴的面积不能确定.
故④错误.
综上所述,①②③正确.
故选:D.
【点睛】本题主要考查旋转的性质、正方形的性质、全等三角形的判定和性质、角平分线的判定,解题的关键是根据旋转的性质绘制辅助线.
5.B
【分析】先证明是等腰直角三角形,即可求出和,用勾股定理即可求解.
【详解】解:∵,,
∴,
∴,
∵旋转的角度为,
∴,
又∵。
∴是等腰直角三角形,
∴,,
∵,
∴,
∴,
在中,,
故选:B.
【点睛】本题考查了几何旋转问题,涉及到等腰直角三角形的性质,灵活运用所学知识是解题关键.
6.A
【详解】由旋转的性质可得,,由等腰三角形的性质及三角形内角和定理即可求解.
【分析】解:将绕点顺时针旋转,点的对应点为点,点的对应点为点,当旋转角为,,,三点在同一直线上,
,,
,
,
,
故选:A.
【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理,掌握旋转的性质是解题的关键.
7.A
【分析】本题考查了旋转的性质、三角形中位线的性质、三角形三边关系、勾股定理,利用勾股定理求出的长,由旋转的性质可得:,,,利用中位线的性质可求,,再根据三角形的三边关系即可求出结果,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,取的中点,连接、,
,
∵,,,
∴,
由旋转的性质可得:,,,
∵点、、分别是、、的中点,
∴是的中位线,是的中位线,
∴,,
当点、、不共线时,,即,
当点在线段上时,,
当点在线段上时,,
综上所述,,
故选:A.
8.A
【分析】连接CF,先证明△ACF为直角三角形,再由△ABC中等面积法求出CF,进而求出AF;再证明△DEF为直角三角形,且G为DE的中点,最后AG=AF-GF即可求解.
【详解】解:连接CF,如下图所示:
∵M是AC的中点,∴MC=MA
∵M是旋转中心,C绕M点旋转后的落点为F
∴MC=MF
∴∠MCF=∠MFC,
∴MA=MC=MF
∴∠MFA=∠A
在△ACF中,由内角和定理知:∠A +∠MFA+∠ACF+∠CFM=180°
故2∠AFM+2∠CFM=180°
∴∠AFC=90°
∴△ACF为直角三角形,CF⊥AB
由△ABC等面积法知:,且AB=5
代入数据解得CF=
∴
∵∠A+∠B=90°,∠A+∠ACF=90°
∴∠ACF=∠B ①
又DF⊥EF,
∴∠AFD+∠AFE=90°
∵∠AFD+∠MFC=90°
∴∠AFE=∠MFC=∠ACF ②
由①、②知:∠B=∠AFE
又由旋转知:∠B=∠E
∴∠AFE=∠E,即GF=GE
由旋转知:∠A=∠D
又∠A=∠AFM
∴∠D=∠AFM,
∴GF=GD
故GF=GE= GD
∴G为Rt△DEF斜边DE上的中点
∴
∴
故答案为:A.
【点睛】本题考查了旋转的性质、直角三角形的判定方法、直角三角形的性质、勾股定理等知识,本题的关键是能连接CF并计算出CF的长.
9.C
【分析】根据正方形的性质可得,,再根据旋转的性质可得,,从而证得,得到,即可求得,可判断①正确;根据正方形的性质可得的长,再根据可得的长,再利用勾股定理可得,可判断②正确;根据题意列出关于面积的一元二次方程,求得有且只有一个实数,使得,可判断③正确;连接,作于点,可得,由,点为的中点,可得,则,从而求得,可判断④错误;即可解题.
【详解】解:四边形是正方形,为对角线,
,,,
线段绕点顺时针旋转得到,
,,
又,,
,
在和中:
,
,
,
,
是直角三角形,
故①正确;
正方形边长为,
,
,,,
,
,
故②正确;
由题可知:,
要,则,
整理得:,
解得:,
有且只有一个实数,使得,
故③正确;
如图,连接,作于点,则,
,
与的边上的高相等,
,点为的中点,
,
,
,
的面积不随着的变化而变化,
故④错误;
故选:C.
【点睛】本题考查了正方形的性质、等腰三角形的判定与性质、全等三角形的判定与性质、勾股定理,解一元二次方程,旋转的性质,直角三角形性质,综合运用以上知识是解题的关键.
10.C
【分析】将绕点顺时针旋转得到,此时与重合,由旋转的性质得到,,,,,推出.根据全等三角形的性质得到,于是得到,故正确;将绕点顺时针旋转得到,连接,通过旋转的性质得出条件证明出利用其性质,在到正方形中去研究;由中推导过程可得出,不能推导出E,F分别为边,的中点,推出是等腰直角三角形,根据等腰直角三角形的性质得到,,求得;故正确;.
【详解】解:A、将绕点顺时针旋转得到,此时与重合,
由旋转可得,,
,,,
,
因此,点,,在同一条直线上.
,
.
,.
即.
在与中,
.
,
故,故A正确,
B、将绕点顺时针旋转得到,连接,
,
,
,
,
,
在和中,
,
,
在正方形中,
,
,
,
即,故正确,
C、由A中可知只能推出,不能说明分别为边,的中点,选项错误;
D、,
是等腰直角三角形,
,,
;故D正确;
故选:C.
【点睛】本题考查四边形综合题、等腰直角三角形性质、旋转的性质、全等三角形的判定和性质等知识,解题的关键是通过旋转作图来解答.
11.3
【分析】由题意以及正方形的性质得OP过正方形ABCD各边的中点时,d最大,求出d的值即可得出答案
【详解】解:如图:设AB的中点是E,OP过点E时,点O与边AB上所有点的连线中,OE最小,此时d=PE最大,
∵正方形ABCD边长为6,O为正方形中心,
∴AE=3,∠OAE=45°,OE⊥AB,
∴OE=3,
∵OP=6,
∴d=PE=6-3=3;
故答案为:3
【点睛】本题考查正方形的性质,旋转的性质,根据题意得出d最大时点P的位置是解题的关键.
12./80度
【分析】根据旋转的性质得到全等的图形即可得到答案.
【详解】解:∵,,
∴ ,
∵是绕顶点O旋转得到,
∴
故答案为.
【点睛】本题考查旋转的性质:旋转后图形与原图形是全等图形,对应角相等,对应边相等.
13.100
【分析】先利用平行线的性质得到,则可计算出,再根据旋转的性质得等于旋转角,然后根据等腰三角形的性质和三角形内角和即可计算出.
【详解】解:∵,
∴,
∵,
∴,
∴,
∵将在平面内绕点A逆时针旋转到的位置,
∴等于旋转角,
∴,
∴,
故答案为:100.
【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形全等同时也考查了平行线的性质.
14.30°,60°或150°
【分析】分四种情况:当CC′=BC′,点C′在△ABC的内部时,如图1,过点C′作C′D⊥BC于点D,C′E⊥AC于点E,可得C′E=AC′,得出∠C′AC=30°,即α=30°;当CC′=BC时,如图2,可证得△ACC′是等边三角形,得出∠CAC′=60°,即α=60°;当BC=BC′时,如图3,可得出∠CAC′=90°,即α=90°,此时△BCC′为等腰直角三角形与题意不含等腰直角三角形不相符,舍去;当CC′=BC′,且点C′在△ABC外部时,如图4,过点C′作C′D⊥BC于点D,过点A作AE⊥C′D于点E,得出AE=AC′,∠AC′E=30°,进而求得∠CAC′=90°+60°=150°,即α=150°.
【详解】解:当CC′=BC′,点C′在△ABC的内部时,如图1,过点C′作C′D⊥BC于点D,C′E⊥AC于点E,取A C′的中点F,连接EF,
∵CC′=BC′,C′D⊥BC,
∴CD=DB=BC,
∵∠ACB=∠C′EC=∠C′DC=90°,
∴四边形CDC′E是矩形,
∴C′E=CD,
∵△ABC是等腰直角三角形,
∴AC=BC,
由旋转得:AC′=AC,
∴C′E=AC′,EF=A C′= C′F,
∴C′E= EF= C′F,
∴三角形C′EF是等边三角形,
∴∠EC′F=60°
∵∠AEC′=90°,
∴∠C′AC=30°,
即α=30°;
当CC′=BC时,如图2,
由旋转得:AC′=AC,
∵CC′=BC,AC=BC,
∴AC=AC′=CC′,
∴△ACC′是等边三角形,
∴∠CAC′=60°,
即α=60°;
当BC=BC′时,如图3,
由旋转得:AC′=AC,
∵BC=BC′=AC,
∴AC=BC=BC′=AC′,
∴四边形ACBC′是菱形,
∵∠ACB=90°,
∴四边形ACBC′是正方形,
∴∠CAC′=90°,
即α=90°,此时△BCC′为等腰直角三角形与题意不含等腰直角三角形不相符,舍去;
当CC′=BC′,且点C′在△ABC外部时,如图4,
过点C′作C′D⊥BC于点D,过点A作AE⊥C′D于点E,取A C′的中点F,连接EF,
则∠AED=∠CDC′=∠ACB=90°,
∴四边形ACDE是矩形,
∴AE=CD,∠CEA=90°,
∵CC′=BC′,C′D⊥BC,
∴CD=BC,
由旋转得AC′=AC,
又∵AC=BC,
∴AE=AC′,EF=A C′=AF,
∴三角形AEF是等边三角形,
∴AE= EF= AF,
∵∠AEC′=90°,
∴∠AC′E=30°,
∴∠C′AE=60°,
∴∠CAC′=90°+60°=150°,
即α=150°;
综上所述,α=30°或60°或150°.
【点睛】本题考查了等腰直角三角形性质,特殊四边形的性质等腰三角形性质,旋转变换的性质,等边三角形的判定和性质,直角三角形30度角的性质等知识,解题的关键是掌握旋转变换的性质,掌握特殊四边形的性质.
15.2或3或5
【分析】求出,,设交于点G,连接.分三种情况,当经过的中点D时,.由旋转性质得到,,得到,得到,根据线段垂直平分线性质得到,得到是等边三角形,得到,即得;当经过的中点E时,,求出,得到,得到,根据,求得,即得;当经过的中点F时, ,可得.
【详解】∵在中,,
∴,
∴,
的垂直平分线经过一边中点,可分为以下三种情况:
经过的中点D;经过的中点E;经过的中点F.
设交于点G,连接,
则.
当经过的中点D时,如图:
,
由旋转知,,
∴,
∴,
连接,
∵垂直平分,
∴,
∴是等边三角形,
∴,
∴,
∴;
当经过的中点E时,如图:
,
∵垂直,
∴,
设,
则,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
当经过的中点F时,如图:
,
∵
∴,
∴.
综上:的长为:2或5或3.
故答案为:2或3或5.
【点睛】此题考查了旋转,熟练掌握旋转的性质,含直角三角形的性质,等边三角形的判定与性质,勾股定理解直角三角形,线段垂直平分线的性质,三角形外角的性质,分类讨论,是解题的关键.
16.(1)证明见解析;(2).
【分析】(1)先根据勾股定理求出BD的长度,然后根据勾股定理的逆定理,即可证明BD⊥BC;
(2)根据两个直角三角形的面积即可求解.
【详解】(1)如图,在Rt△ABD中,∠BAD=90°,AB=4m,AD=3m,由勾股定理得:BD=5m,
∵BC=13m,CD=12m,BD=5m.
∴BD2+DC2=BC2,
∴∠BDC=90°,
即BD⊥DC;
(2)如图,四边形ABCD的面积是
S△ABD+S△BDC=×3×4+×5×12=36.
【点睛】本题考查勾股定理、勾股定理的逆定理、三角形面积公式等知识,解题的关键是用勾股定理逆定理推出直角三角形,再求三角形面积.
17.(1)见解析,B1 (3,3),C1 (7,3);(2)见解析,B2 (6,4),C2 (6,8)
【分析】(1)根据图形平移的性质画出平移后的△A1B1C1,结合图形可得出B1,C1两点的坐标;
(2)根据图形旋转的性质画出旋转后的△A2 B2C2,结合图形可得出B2,C2两点的坐标.
【详解】解:如图,即为所求,,两点的坐标分别为,.
如图,即为所求,,两点的坐标分别为,.
【点睛】本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.
18.(1)见解析
(2)
【分析】(1)先画出点A、B、C关于x轴对称的对应点,再依次连接即可;
(2)用割补法求解即可.
【详解】(1)解:如图所示,即为所求:
(2)解:的面积.
【点睛】本题主要考查了轴对称图形的画法及对直角坐标系的认识,其中掌握轴对称图形的画法,以及用个割补法求面积是做题的关键.
19.(1)画图见解析
(2)
【分析】(1)补成网格结构,找出A,B旋转后的对应点、的位置,然后顺次连接即可;
(2)根据的位置可得的坐标.
【详解】(1)解:如图,即为所求作的三角形,
(2)由的位置可得:.
【点睛】本题考查的是旋转的性质,画旋转图形,熟记旋转的性质并进行画图是解本题的关键.
20.(1)见解析
(2)见解析
【分析】(1)根据平移的性质可将点、、向下平移3个单位长度,再向右平移2个单位长度,再把平移后得到的点连接,即可得到;
(2)取的中点,根据旋转的性质将、分别绕点顺时针旋转,把旋转后所得到的点连接,即可得到.
【详解】(1)如图,即为所求.
(2)如图,即为所求.
【点睛】本题考查了平移变换和旋转变换作图,熟练掌握旋转和平移的性质是解决问题的关键.
21.(1)EF =2.5;(2)证明见解析;(3)(1)中的结论仍然成立.理由见解析.
【详解】试题分析:(1)等腰直角三角形的斜边长是直角边的 倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
(2)连接CF,需要证明 是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得 从而 ,再根据直角三角形斜边上的中线是斜边的一半,得 ,得证 是等腰直角三角形,结论得证;
(3)连接CF,延长EF交CB于点G,利用ASA证明△EDF≌△GBF,得出EF=GF,BG=DE=AE,进而证明CE=CG,得出△CEF为等腰直角三角形,利用三线合一证明 结论得证.
试题解析:
(1)∵∠AED=90°,AE=DE,AD=3,
∴AE=DE=3,
在Rt△BDE中,
∵DE=3,BE=4,
∴BD=5,
又∵F是线段BD的中点,
∴EF=BD=2.5;
(2)连接CF,线段CE与FE之间的数量关系是CE=FE;
∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE=EF.
(3)(1)中的结论仍然成立.
如图,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
在△EDF和△GBF中,
,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=FE;
【方法点睛】本题目用的知识点:(1)直角三角形斜边上的中线是斜边的一半;(2)当看到两条线段的比是时,想方设法去转化到等腰直角三角形的斜边和腰上,因为等腰三角形斜边长是腰长的 倍;(3)等腰三角形的三线合一;(4)四点共圆,利用圆的观点类解决问题,简便易行.
22.(1)见解析;(2)a ; 或
【分析】(1)根据旋转图形的性质,点C与点B是对应点,点E点F是对应点,分别作线段BC、EF的垂直平分线的交点就是旋转中心点G.
(2)由旋转的性质可以得出FG=EG,∠FGE=90°,设EC=x,利用勾股定理及三角形的面积公式建立等量关系,就可以求出结论.
【详解】(1)如图:分别作线段BC、EF的垂直平分线的交点就是旋转中心点G.
(2)∵G是旋转中心,且四边形ABCD是正方形,
∴FG=EG,∠FGE=90°
∵S△FGE=,且由勾股定理,得2FG2=EF2,
∴S△FGE=,
设EC=x,则BF=x,BE=2a-x,在Rt△BEF中,由勾股定理,得
EF2=x2+(2a-x)2,
∴S△FGE=,
∵S△FBE=,
①当S△FGE=S△FBE时,则
,
解得:x=a;
∴EC=a.
②当S△FGE=3S△FBE时,则,
∴2x2-4ax+a2=0,
解得:x=或x=,
∴EC=或EC=.
考查了旋转对称图形的性质,正方形的性质,三角形的面积及勾股定理的运用.
【点睛】考查了旋转对称图形的性质,正方形的性质,三角形的面积及勾股定理的运用.
23.(1)证明见解析;(2);(3)CG=6
【分析】(1)过点C作CP⊥AB于点P,作CQ⊥AD的延长线于点Q,证明△CQD≌△CPB,即可得到答案;
(2)延长ED,让MD=ED,△AME是等边三角形,然后利用等边三角形的性质和角平分线的定义即可求得答案;
(3)延长GC,过点F作FK⊥GC的延长线于点K,过点H作HL⊥GF于点L,连接HF,通过证明△CFK≌△HFL,得到FK=FL,又有直角三角形中所对的直角边是斜边的一半,求得FK=GF,根据等腰三角形的三线合一,进一步求得∠FGH=,从求得到∠GCH=,然后在直角三角形中利用勾股定理求解即可得答案.
【详解】解:(1)过点C作CP⊥AB于点P,作CQ⊥AD的延长线于点Q,如下图:
∵AC平分∠DAB,CP⊥AB,CQ⊥AD
∴CQ=CP
在四边形APCQ中,∠APC=∠AQC=
∴∠QAP+∠PCQ=
又∵∠DAB+∠DCB=180°
∴∠PCQ=∠DCB
∴∠QCD+∠DCP=∠DCP+∠PCB
∴∠QCD=∠PCB
又∵∠CQD=∠CPB=
∴△CQD≌△CPB(ASA)
∴CD=CB
(2)延长ED,让MD=ED,如下图:
∵∠ADB=90°
∴AD⊥ME
又∵MD=ED
∴AM=AE,ME=2DE
又∵AE=2DE
∴ME=AE=AM
∴△AME是等边三角形
∴
又∵∠ADE=90°
∴
∵AC平分∠DAB
∴
又∵
∴
(3)延长GC,过点F作FK⊥GC的延长线于点K,过点H作HL⊥GF于点L,连接HF,如下图:
∵在中,
∴∠HCB=
又∵折叠
∴CH=CF, ∠HCB=∠FCB=
∴∠HCF=
∴△CHF是等边三角形
∴∠CFH=∠CHF=,CF=HF
又∵在中,∠CGF=,∠GKF=
∴∠GFK=
∴∠CFH=∠GFK
∴∠CFK+∠CFG=∠CFG+∠HFL
∴∠CFK=∠HFL
又∵∠CKF=∠LHF=,CF=HF
∴△CFK≌△HFL
∴FK=FL
又∵在中,∠CGF=
∴FK=GF
∴FL=GF
∴GL=FL
又∵HL⊥GF
∴HG=HF
∴∠FGH=∠GFH
又∵∠CHF=,∠CHB=
∴∠FHB=∠CHB-∠CHF=
∴∠FGH=
∴∠CGH=∠CGF+∠FGH=
又∵∠CHG=
∴∠GCH=
∴GH=CH,△GCH是等腰直角三角形
又∵
∴
∴
在中,由勾股定理得:
∵CG>0
∴CG=6
【点睛】本题考查全等三角形的性质和判定,含的直角三角形性质,等边三角形的性质和判定,直角三角形的勾股定理等知识点,能够熟练利用化归的思想和数形结合的思想去解题,是本题的重点.
21世纪教育网(www.21cnjy.com)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.经过下列变换,能由图①所示的基本图形得到图②的是( )
A.旋转 B.中心对称和轴对称
C.平移和轴对称 D.中心对称
2.如图,绕点O逆时针旋转,得到,若,则等于( )
A. B. C. D.
3.如图,将斜边长为4的直角三角板放在直角坐标系中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转后点P的对应点Q的坐标是( )
A. B. C. D.
4.如图,在正方形中,,且则以下结论:平分;;的周长为;的面积等于正方形的面积的一半.其中正确的个数是( )
A.个 B.个 C.个 D.个
5.把一副三角板按图甲所示的方式放置,其中,,,,,把三角板绕点C顺时针旋转得到 (如图乙),与交于点O,连接,则线段的长为( )
A.6 B.10 C.8 D.
6.如图,将绕点顺时针旋转,点的对应点为点,点的对应点为点,当旋转角为,,,三点在同一直线上时,则的度数为( )
A. B. C. D.
7.如图,在中,,,.将绕点旋 得,分别取,的中点,,则的取值范围是( )
A. B. C. D.
8.如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
9.如图,正方形边长为,从出发沿对角线向运动,连接,将线段绕点顺时针旋转得到,连接,设,下列说法:①是直角三角形;②当时,;③有且只有一个实数,使得;④取中点,连接,,的面积随着的增大而增大.正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形中,点E,F分别为边,上的点,连接,,与对角线分别交于点G,H,连接.若,则下列判断错误的是( )
A. B.
C.E,F分别为边,的中点 D.
二、填空题
11.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为6,中心为O,在正方形外有一点P,,当正方形绕着点O旋转时,则点P到正方形的最短距离d的最大值为 .
12.将三角形 绕顶点O旋转到如图所示的位置,若,,则 .
13.如图,在,将在平面内绕点A逆时针旋转到的位置,连接.若,则旋转角的度数为 °.
14.如图,已知是等腰直角三角形,,将线段AC绕点A逆时针旋转得到,连接,.当是等腰三角形(不含等腰直角三角形)时, .
15.如图,在中,,点P为上一点,将线段绕点P顺时针旋转得线段,点Q在射线上,当的垂直平分线经过一边中点时,的长为 .
三、解答题
16.如图,一块四边形的土地,其中,,,,.
(1)试说明;
(2)求这块土地的面积.
17.在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)把平移后,点A移到点,,画出平移后得到的,并写出、的坐标;
(2)把绕点按逆时针方向旋转90°,画出旋转后的,并写出B2、C2的坐标.
18.如图,在平面直角坐标系中,的位置如图所示,每个小正方形边长为单位1,的三个顶点分别在正方形格点上.
(1)请画出关于x轴对称的图形;
(2)直接写出的面积.
19.在平面直角坐标系中,的位置如图所示,且点,.
(1)画出绕点O顺时针旋转后得到的;
(2)直接写出点A的对称点的坐标.
20.如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点).
(1)将向下平移3个单位长度,再向右平移2个单位长度,得到,请画出;
(2)已知点M为的中点,以点M为旋转中心,将线段顺时针旋转,得到线段,请画出线段.
21.如图1,在△ACB和△AED中,AC=BC,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=6,BE=8,求EF的长;
(2)求证:CE=EF;
(3)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立?并说明理由.
22.如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
(1)请画出旋转中心G (保留画图痕迹),并连接GF,GE;
(2)若正方形的边长为2a,当CE= 时,S△FGE=S△FBE;当CE= 时,S△FGE=3S△FBE.
23.在四边形ABCD中,∠DAB+∠DCB=180°,AC平分∠DAB.
(1)如图1,求证:BC=CD;
(2)如图2,连接BD交AC于点E,若∠ADB=90°,AE=2DE,求∠ABD的度数;
(3)如图3,在(2)的条件下,过点C作CH⊥AB于点H,△BCH沿BC翻折,点H的对应点为点F,点G在线段AB上,连接FG,若∠CGF=30°,S△CHG=9,求线段CG的长.
21世纪教育网(www.21cnjy.com)
1.A
【分析】根据旋转,中心对称,轴对称和平移的性质求解即可.
【详解】A中,经过旋转能由基本图形得到题图②,故该选项符合题意;
B中,经过中心对称和轴对称不能由基本图形得到题图②,故该选项不符合题意;
C中,经过平移和轴对称不能由基本图形得到题图②,故该选项不符合题意;
D中,只经过中心对称不能由基本图形得到题图②,故该选项符合题意,
故选:A.
【点睛】此题考查了旋转,中心对称,轴对称和平移的性质,解题的关键是熟练掌握旋转,中心对称,轴对称和平移的性质.旋转的特性∶不改变图形的形状和大小;经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.对应角相等,对应线段也相等.平移的特性∶平移只改变图形的位置,不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等.轴对称图形的特性∶关于某直线对称的两个图形是全等的;图形的对应点连线段被同一条直线垂直平分;对应线段或延长线与对称轴交于一点.
2.C
【分析】本题考查了旋转的性质,确定旋转角以及旋转前后对应角相等是解题关键.
【详解】解:由题意得:,,
∴,
故选:C
3.B
【分析】如图所示,连接,过Q作轴,由旋转的性质可得,由直角三角形斜边上的中线等于斜边的一半得到,则,进而推出,,由旋转的性质得到,则,再分别求出的长即可得到答案.
【详解】解:如图所示,连接,过Q作轴,
由旋转的性质可得,
∵,P为斜边的中点.
∴,
∴,
∴,
∴,
∴,
∴
在中,,
∴,,
∴P的对应点Q的坐标为,
故选B.
【点睛】本题主要考查了坐标与图形变化——旋转,含30度角的直角三角形的性质,勾股定理,直角三角形斜边上的中线,等腰三角形的性质与判定等等,灵活运用所学知识是解题的关键.
4.D
【分析】将绕点顺时针旋转得,然后证明≌,再逐一判断即可.
【详解】如图,将绕点顺时针旋转得到.
根据旋转的性质,得
,,,,.
①∵,
∴.
∴.
在和中,
∴,
∴.
∴.
∴平分.
故①正确.
②∵,
∴,
故②正确.
③.
故③正确.
④∵,
∴.
∵的长度不固定,
∴的面积不能确定.
故④错误.
综上所述,①②③正确.
故选:D.
【点睛】本题主要考查旋转的性质、正方形的性质、全等三角形的判定和性质、角平分线的判定,解题的关键是根据旋转的性质绘制辅助线.
5.B
【分析】先证明是等腰直角三角形,即可求出和,用勾股定理即可求解.
【详解】解:∵,,
∴,
∴,
∵旋转的角度为,
∴,
又∵。
∴是等腰直角三角形,
∴,,
∵,
∴,
∴,
在中,,
故选:B.
【点睛】本题考查了几何旋转问题,涉及到等腰直角三角形的性质,灵活运用所学知识是解题关键.
6.A
【详解】由旋转的性质可得,,由等腰三角形的性质及三角形内角和定理即可求解.
【分析】解:将绕点顺时针旋转,点的对应点为点,点的对应点为点,当旋转角为,,,三点在同一直线上,
,,
,
,
,
故选:A.
【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理,掌握旋转的性质是解题的关键.
7.A
【分析】本题考查了旋转的性质、三角形中位线的性质、三角形三边关系、勾股定理,利用勾股定理求出的长,由旋转的性质可得:,,,利用中位线的性质可求,,再根据三角形的三边关系即可求出结果,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,取的中点,连接、,
,
∵,,,
∴,
由旋转的性质可得:,,,
∵点、、分别是、、的中点,
∴是的中位线,是的中位线,
∴,,
当点、、不共线时,,即,
当点在线段上时,,
当点在线段上时,,
综上所述,,
故选:A.
8.A
【分析】连接CF,先证明△ACF为直角三角形,再由△ABC中等面积法求出CF,进而求出AF;再证明△DEF为直角三角形,且G为DE的中点,最后AG=AF-GF即可求解.
【详解】解:连接CF,如下图所示:
∵M是AC的中点,∴MC=MA
∵M是旋转中心,C绕M点旋转后的落点为F
∴MC=MF
∴∠MCF=∠MFC,
∴MA=MC=MF
∴∠MFA=∠A
在△ACF中,由内角和定理知:∠A +∠MFA+∠ACF+∠CFM=180°
故2∠AFM+2∠CFM=180°
∴∠AFC=90°
∴△ACF为直角三角形,CF⊥AB
由△ABC等面积法知:,且AB=5
代入数据解得CF=
∴
∵∠A+∠B=90°,∠A+∠ACF=90°
∴∠ACF=∠B ①
又DF⊥EF,
∴∠AFD+∠AFE=90°
∵∠AFD+∠MFC=90°
∴∠AFE=∠MFC=∠ACF ②
由①、②知:∠B=∠AFE
又由旋转知:∠B=∠E
∴∠AFE=∠E,即GF=GE
由旋转知:∠A=∠D
又∠A=∠AFM
∴∠D=∠AFM,
∴GF=GD
故GF=GE= GD
∴G为Rt△DEF斜边DE上的中点
∴
∴
故答案为:A.
【点睛】本题考查了旋转的性质、直角三角形的判定方法、直角三角形的性质、勾股定理等知识,本题的关键是能连接CF并计算出CF的长.
9.C
【分析】根据正方形的性质可得,,再根据旋转的性质可得,,从而证得,得到,即可求得,可判断①正确;根据正方形的性质可得的长,再根据可得的长,再利用勾股定理可得,可判断②正确;根据题意列出关于面积的一元二次方程,求得有且只有一个实数,使得,可判断③正确;连接,作于点,可得,由,点为的中点,可得,则,从而求得,可判断④错误;即可解题.
【详解】解:四边形是正方形,为对角线,
,,,
线段绕点顺时针旋转得到,
,,
又,,
,
在和中:
,
,
,
,
是直角三角形,
故①正确;
正方形边长为,
,
,,,
,
,
故②正确;
由题可知:,
要,则,
整理得:,
解得:,
有且只有一个实数,使得,
故③正确;
如图,连接,作于点,则,
,
与的边上的高相等,
,点为的中点,
,
,
,
的面积不随着的变化而变化,
故④错误;
故选:C.
【点睛】本题考查了正方形的性质、等腰三角形的判定与性质、全等三角形的判定与性质、勾股定理,解一元二次方程,旋转的性质,直角三角形性质,综合运用以上知识是解题的关键.
10.C
【分析】将绕点顺时针旋转得到,此时与重合,由旋转的性质得到,,,,,推出.根据全等三角形的性质得到,于是得到,故正确;将绕点顺时针旋转得到,连接,通过旋转的性质得出条件证明出利用其性质,在到正方形中去研究;由中推导过程可得出,不能推导出E,F分别为边,的中点,推出是等腰直角三角形,根据等腰直角三角形的性质得到,,求得;故正确;.
【详解】解:A、将绕点顺时针旋转得到,此时与重合,
由旋转可得,,
,,,
,
因此,点,,在同一条直线上.
,
.
,.
即.
在与中,
.
,
故,故A正确,
B、将绕点顺时针旋转得到,连接,
,
,
,
,
,
在和中,
,
,
在正方形中,
,
,
,
即,故正确,
C、由A中可知只能推出,不能说明分别为边,的中点,选项错误;
D、,
是等腰直角三角形,
,,
;故D正确;
故选:C.
【点睛】本题考查四边形综合题、等腰直角三角形性质、旋转的性质、全等三角形的判定和性质等知识,解题的关键是通过旋转作图来解答.
11.3
【分析】由题意以及正方形的性质得OP过正方形ABCD各边的中点时,d最大,求出d的值即可得出答案
【详解】解:如图:设AB的中点是E,OP过点E时,点O与边AB上所有点的连线中,OE最小,此时d=PE最大,
∵正方形ABCD边长为6,O为正方形中心,
∴AE=3,∠OAE=45°,OE⊥AB,
∴OE=3,
∵OP=6,
∴d=PE=6-3=3;
故答案为:3
【点睛】本题考查正方形的性质,旋转的性质,根据题意得出d最大时点P的位置是解题的关键.
12./80度
【分析】根据旋转的性质得到全等的图形即可得到答案.
【详解】解:∵,,
∴ ,
∵是绕顶点O旋转得到,
∴
故答案为.
【点睛】本题考查旋转的性质:旋转后图形与原图形是全等图形,对应角相等,对应边相等.
13.100
【分析】先利用平行线的性质得到,则可计算出,再根据旋转的性质得等于旋转角,然后根据等腰三角形的性质和三角形内角和即可计算出.
【详解】解:∵,
∴,
∵,
∴,
∴,
∵将在平面内绕点A逆时针旋转到的位置,
∴等于旋转角,
∴,
∴,
故答案为:100.
【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形全等同时也考查了平行线的性质.
14.30°,60°或150°
【分析】分四种情况:当CC′=BC′,点C′在△ABC的内部时,如图1,过点C′作C′D⊥BC于点D,C′E⊥AC于点E,可得C′E=AC′,得出∠C′AC=30°,即α=30°;当CC′=BC时,如图2,可证得△ACC′是等边三角形,得出∠CAC′=60°,即α=60°;当BC=BC′时,如图3,可得出∠CAC′=90°,即α=90°,此时△BCC′为等腰直角三角形与题意不含等腰直角三角形不相符,舍去;当CC′=BC′,且点C′在△ABC外部时,如图4,过点C′作C′D⊥BC于点D,过点A作AE⊥C′D于点E,得出AE=AC′,∠AC′E=30°,进而求得∠CAC′=90°+60°=150°,即α=150°.
【详解】解:当CC′=BC′,点C′在△ABC的内部时,如图1,过点C′作C′D⊥BC于点D,C′E⊥AC于点E,取A C′的中点F,连接EF,
∵CC′=BC′,C′D⊥BC,
∴CD=DB=BC,
∵∠ACB=∠C′EC=∠C′DC=90°,
∴四边形CDC′E是矩形,
∴C′E=CD,
∵△ABC是等腰直角三角形,
∴AC=BC,
由旋转得:AC′=AC,
∴C′E=AC′,EF=A C′= C′F,
∴C′E= EF= C′F,
∴三角形C′EF是等边三角形,
∴∠EC′F=60°
∵∠AEC′=90°,
∴∠C′AC=30°,
即α=30°;
当CC′=BC时,如图2,
由旋转得:AC′=AC,
∵CC′=BC,AC=BC,
∴AC=AC′=CC′,
∴△ACC′是等边三角形,
∴∠CAC′=60°,
即α=60°;
当BC=BC′时,如图3,
由旋转得:AC′=AC,
∵BC=BC′=AC,
∴AC=BC=BC′=AC′,
∴四边形ACBC′是菱形,
∵∠ACB=90°,
∴四边形ACBC′是正方形,
∴∠CAC′=90°,
即α=90°,此时△BCC′为等腰直角三角形与题意不含等腰直角三角形不相符,舍去;
当CC′=BC′,且点C′在△ABC外部时,如图4,
过点C′作C′D⊥BC于点D,过点A作AE⊥C′D于点E,取A C′的中点F,连接EF,
则∠AED=∠CDC′=∠ACB=90°,
∴四边形ACDE是矩形,
∴AE=CD,∠CEA=90°,
∵CC′=BC′,C′D⊥BC,
∴CD=BC,
由旋转得AC′=AC,
又∵AC=BC,
∴AE=AC′,EF=A C′=AF,
∴三角形AEF是等边三角形,
∴AE= EF= AF,
∵∠AEC′=90°,
∴∠AC′E=30°,
∴∠C′AE=60°,
∴∠CAC′=90°+60°=150°,
即α=150°;
综上所述,α=30°或60°或150°.
【点睛】本题考查了等腰直角三角形性质,特殊四边形的性质等腰三角形性质,旋转变换的性质,等边三角形的判定和性质,直角三角形30度角的性质等知识,解题的关键是掌握旋转变换的性质,掌握特殊四边形的性质.
15.2或3或5
【分析】求出,,设交于点G,连接.分三种情况,当经过的中点D时,.由旋转性质得到,,得到,得到,根据线段垂直平分线性质得到,得到是等边三角形,得到,即得;当经过的中点E时,,求出,得到,得到,根据,求得,即得;当经过的中点F时, ,可得.
【详解】∵在中,,
∴,
∴,
的垂直平分线经过一边中点,可分为以下三种情况:
经过的中点D;经过的中点E;经过的中点F.
设交于点G,连接,
则.
当经过的中点D时,如图:
,
由旋转知,,
∴,
∴,
连接,
∵垂直平分,
∴,
∴是等边三角形,
∴,
∴,
∴;
当经过的中点E时,如图:
,
∵垂直,
∴,
设,
则,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
当经过的中点F时,如图:
,
∵
∴,
∴.
综上:的长为:2或5或3.
故答案为:2或3或5.
【点睛】此题考查了旋转,熟练掌握旋转的性质,含直角三角形的性质,等边三角形的判定与性质,勾股定理解直角三角形,线段垂直平分线的性质,三角形外角的性质,分类讨论,是解题的关键.
16.(1)证明见解析;(2).
【分析】(1)先根据勾股定理求出BD的长度,然后根据勾股定理的逆定理,即可证明BD⊥BC;
(2)根据两个直角三角形的面积即可求解.
【详解】(1)如图,在Rt△ABD中,∠BAD=90°,AB=4m,AD=3m,由勾股定理得:BD=5m,
∵BC=13m,CD=12m,BD=5m.
∴BD2+DC2=BC2,
∴∠BDC=90°,
即BD⊥DC;
(2)如图,四边形ABCD的面积是
S△ABD+S△BDC=×3×4+×5×12=36.
【点睛】本题考查勾股定理、勾股定理的逆定理、三角形面积公式等知识,解题的关键是用勾股定理逆定理推出直角三角形,再求三角形面积.
17.(1)见解析,B1 (3,3),C1 (7,3);(2)见解析,B2 (6,4),C2 (6,8)
【分析】(1)根据图形平移的性质画出平移后的△A1B1C1,结合图形可得出B1,C1两点的坐标;
(2)根据图形旋转的性质画出旋转后的△A2 B2C2,结合图形可得出B2,C2两点的坐标.
【详解】解:如图,即为所求,,两点的坐标分别为,.
如图,即为所求,,两点的坐标分别为,.
【点睛】本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.
18.(1)见解析
(2)
【分析】(1)先画出点A、B、C关于x轴对称的对应点,再依次连接即可;
(2)用割补法求解即可.
【详解】(1)解:如图所示,即为所求:
(2)解:的面积.
【点睛】本题主要考查了轴对称图形的画法及对直角坐标系的认识,其中掌握轴对称图形的画法,以及用个割补法求面积是做题的关键.
19.(1)画图见解析
(2)
【分析】(1)补成网格结构,找出A,B旋转后的对应点、的位置,然后顺次连接即可;
(2)根据的位置可得的坐标.
【详解】(1)解:如图,即为所求作的三角形,
(2)由的位置可得:.
【点睛】本题考查的是旋转的性质,画旋转图形,熟记旋转的性质并进行画图是解本题的关键.
20.(1)见解析
(2)见解析
【分析】(1)根据平移的性质可将点、、向下平移3个单位长度,再向右平移2个单位长度,再把平移后得到的点连接,即可得到;
(2)取的中点,根据旋转的性质将、分别绕点顺时针旋转,把旋转后所得到的点连接,即可得到.
【详解】(1)如图,即为所求.
(2)如图,即为所求.
【点睛】本题考查了平移变换和旋转变换作图,熟练掌握旋转和平移的性质是解决问题的关键.
21.(1)EF =2.5;(2)证明见解析;(3)(1)中的结论仍然成立.理由见解析.
【详解】试题分析:(1)等腰直角三角形的斜边长是直角边的 倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
(2)连接CF,需要证明 是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得 从而 ,再根据直角三角形斜边上的中线是斜边的一半,得 ,得证 是等腰直角三角形,结论得证;
(3)连接CF,延长EF交CB于点G,利用ASA证明△EDF≌△GBF,得出EF=GF,BG=DE=AE,进而证明CE=CG,得出△CEF为等腰直角三角形,利用三线合一证明 结论得证.
试题解析:
(1)∵∠AED=90°,AE=DE,AD=3,
∴AE=DE=3,
在Rt△BDE中,
∵DE=3,BE=4,
∴BD=5,
又∵F是线段BD的中点,
∴EF=BD=2.5;
(2)连接CF,线段CE与FE之间的数量关系是CE=FE;
∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE=EF.
(3)(1)中的结论仍然成立.
如图,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
在△EDF和△GBF中,
,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=FE;
【方法点睛】本题目用的知识点:(1)直角三角形斜边上的中线是斜边的一半;(2)当看到两条线段的比是时,想方设法去转化到等腰直角三角形的斜边和腰上,因为等腰三角形斜边长是腰长的 倍;(3)等腰三角形的三线合一;(4)四点共圆,利用圆的观点类解决问题,简便易行.
22.(1)见解析;(2)a ; 或
【分析】(1)根据旋转图形的性质,点C与点B是对应点,点E点F是对应点,分别作线段BC、EF的垂直平分线的交点就是旋转中心点G.
(2)由旋转的性质可以得出FG=EG,∠FGE=90°,设EC=x,利用勾股定理及三角形的面积公式建立等量关系,就可以求出结论.
【详解】(1)如图:分别作线段BC、EF的垂直平分线的交点就是旋转中心点G.
(2)∵G是旋转中心,且四边形ABCD是正方形,
∴FG=EG,∠FGE=90°
∵S△FGE=,且由勾股定理,得2FG2=EF2,
∴S△FGE=,
设EC=x,则BF=x,BE=2a-x,在Rt△BEF中,由勾股定理,得
EF2=x2+(2a-x)2,
∴S△FGE=,
∵S△FBE=,
①当S△FGE=S△FBE时,则
,
解得:x=a;
∴EC=a.
②当S△FGE=3S△FBE时,则,
∴2x2-4ax+a2=0,
解得:x=或x=,
∴EC=或EC=.
考查了旋转对称图形的性质,正方形的性质,三角形的面积及勾股定理的运用.
【点睛】考查了旋转对称图形的性质,正方形的性质,三角形的面积及勾股定理的运用.
23.(1)证明见解析;(2);(3)CG=6
【分析】(1)过点C作CP⊥AB于点P,作CQ⊥AD的延长线于点Q,证明△CQD≌△CPB,即可得到答案;
(2)延长ED,让MD=ED,△AME是等边三角形,然后利用等边三角形的性质和角平分线的定义即可求得答案;
(3)延长GC,过点F作FK⊥GC的延长线于点K,过点H作HL⊥GF于点L,连接HF,通过证明△CFK≌△HFL,得到FK=FL,又有直角三角形中所对的直角边是斜边的一半,求得FK=GF,根据等腰三角形的三线合一,进一步求得∠FGH=,从求得到∠GCH=,然后在直角三角形中利用勾股定理求解即可得答案.
【详解】解:(1)过点C作CP⊥AB于点P,作CQ⊥AD的延长线于点Q,如下图:
∵AC平分∠DAB,CP⊥AB,CQ⊥AD
∴CQ=CP
在四边形APCQ中,∠APC=∠AQC=
∴∠QAP+∠PCQ=
又∵∠DAB+∠DCB=180°
∴∠PCQ=∠DCB
∴∠QCD+∠DCP=∠DCP+∠PCB
∴∠QCD=∠PCB
又∵∠CQD=∠CPB=
∴△CQD≌△CPB(ASA)
∴CD=CB
(2)延长ED,让MD=ED,如下图:
∵∠ADB=90°
∴AD⊥ME
又∵MD=ED
∴AM=AE,ME=2DE
又∵AE=2DE
∴ME=AE=AM
∴△AME是等边三角形
∴
又∵∠ADE=90°
∴
∵AC平分∠DAB
∴
又∵
∴
(3)延长GC,过点F作FK⊥GC的延长线于点K,过点H作HL⊥GF于点L,连接HF,如下图:
∵在中,
∴∠HCB=
又∵折叠
∴CH=CF, ∠HCB=∠FCB=
∴∠HCF=
∴△CHF是等边三角形
∴∠CFH=∠CHF=,CF=HF
又∵在中,∠CGF=,∠GKF=
∴∠GFK=
∴∠CFH=∠GFK
∴∠CFK+∠CFG=∠CFG+∠HFL
∴∠CFK=∠HFL
又∵∠CKF=∠LHF=,CF=HF
∴△CFK≌△HFL
∴FK=FL
又∵在中,∠CGF=
∴FK=GF
∴FL=GF
∴GL=FL
又∵HL⊥GF
∴HG=HF
∴∠FGH=∠GFH
又∵∠CHF=,∠CHB=
∴∠FHB=∠CHB-∠CHF=
∴∠FGH=
∴∠CGH=∠CGF+∠FGH=
又∵∠CHG=
∴∠GCH=
∴GH=CH,△GCH是等腰直角三角形
又∵
∴
∴
在中,由勾股定理得:
∵CG>0
∴CG=6
【点睛】本题考查全等三角形的性质和判定,含的直角三角形性质,等边三角形的性质和判定,直角三角形的勾股定理等知识点,能够熟练利用化归的思想和数形结合的思想去解题,是本题的重点.
21世纪教育网(www.21cnjy.com)
同课章节目录
