直线与圆锥曲线 导学案
图片预览



文档简介
直线与圆锥曲线
第一课时
学习目标
1.理解直线与圆锥曲线位置关系的判断方法;
2.会判断已知直线和圆锥曲线的位置关系;
3.能够根据直线与圆锥曲线的位置关系求相应参数的取值范围;
学习过程
【任务一】阅读教材
阅读课本P67页例1、例2。仿照例题解法完成下面问题
仿照练习1:已知直线和椭圆,当取何值时,此直线与椭圆:(1)相交;(2)相切;(3)相离。
仿照练习2:已知直线与椭圆相交于不同的两点,求的取值范围。
【任务二】典型例题分析
例1:已知椭圆,弦的中点是,求弦所在的直线方程。
变式练习1:已知是直线被椭圆所截的线段的中点,求直线的方程。
例2:已知直线与双曲线相交于两点,是坐标原点,如果,求的值。
变式练习2:设抛物线与其过焦点的斜率为的直线相交于两点,是坐标原点,求的值。
作业:直线过点且与抛物线只有一个公共点,求直线的方程。
第二课时
学习目标
理解直线与圆锥曲线位置关系的判断方式;
能够根据根与系数的关系推导出弦长公式,并会应用弦长公式解决问题;
了解函数求最值的相关解决问题的方法。
学习过程
【任务一】阅读课本
阅读课本P68也例3.仿照例3的解法完成下面问题;
仿照练习:已知抛物线的弦过它的焦点,直线的斜率为2,求的长。
【任务二】典型例题分析
例1:已知斜率为的直线与抛物线相交于两点,如果线段的长等于,求直线的方程。
变式练习:已知抛物线的顶点在原点,对称轴是轴,它的弦所在直线的方程为,弦长等于,求抛物线的方程。
例2:已知直线与椭圆相交于两点,当变化时,求的最大值。
变式练习2:已知椭圆的离心率为,且经过点.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点的直线交椭圆于,两点,求△(为原点)面积的最大值。
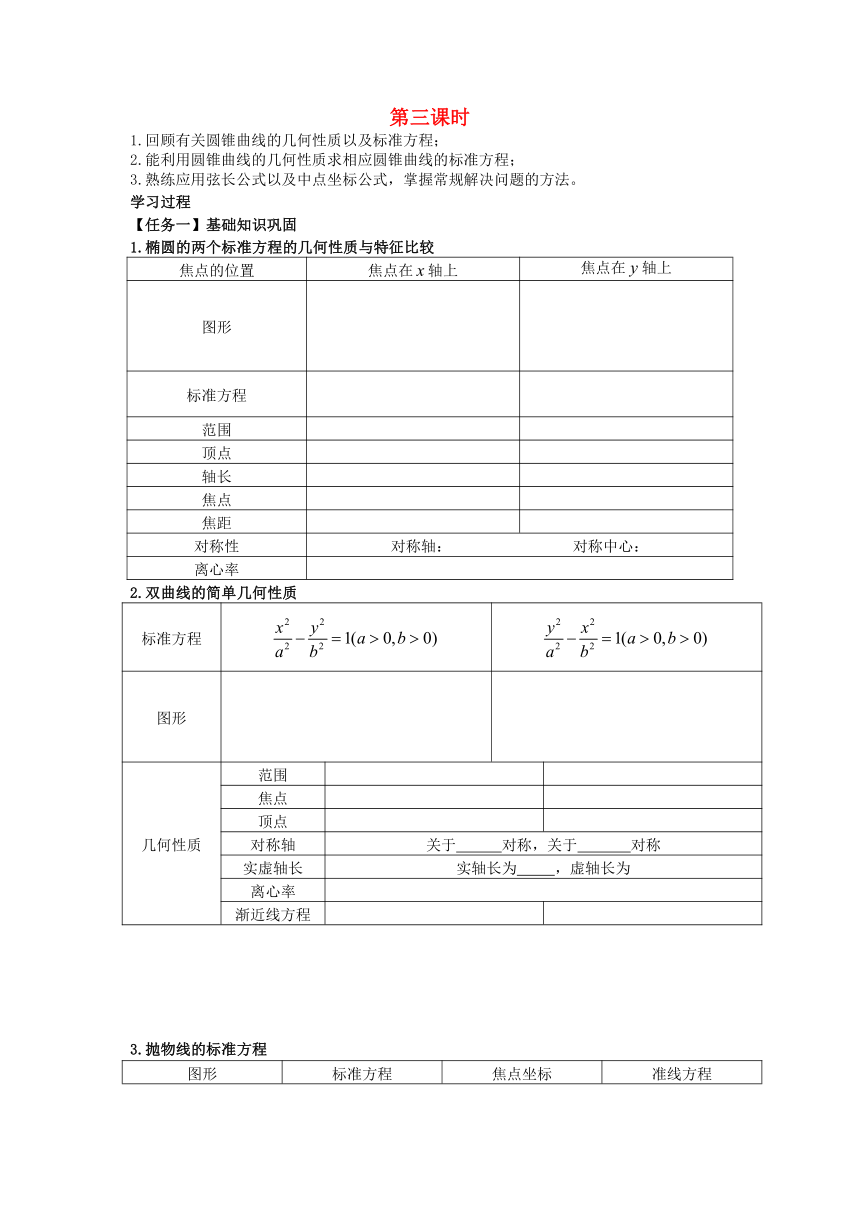
第三课时
回顾有关圆锥曲线的几何性质以及标准方程;
能利用圆锥曲线的几何性质求相应圆锥曲线的标准方程;
熟练应用弦长公式以及中点坐标公式,掌握常规解决问题的方法。
学习过程
【任务一】基础知识巩固
1.椭圆的两个标准方程的几何性质与特征比较
焦点的位置 焦点在轴上 焦点在轴上
图形
标准方程
范围
顶点
轴长
焦点
焦距
对称性 对称轴: 对称中心:
离心率
2.双曲线的简单几何性质
标准方程
图形
几何性质 范围
焦点
顶点
对称轴 关于 对称,关于 对称
实虚轴长 实轴长为 ,虚轴长为
离心率
渐近线方程
3.抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
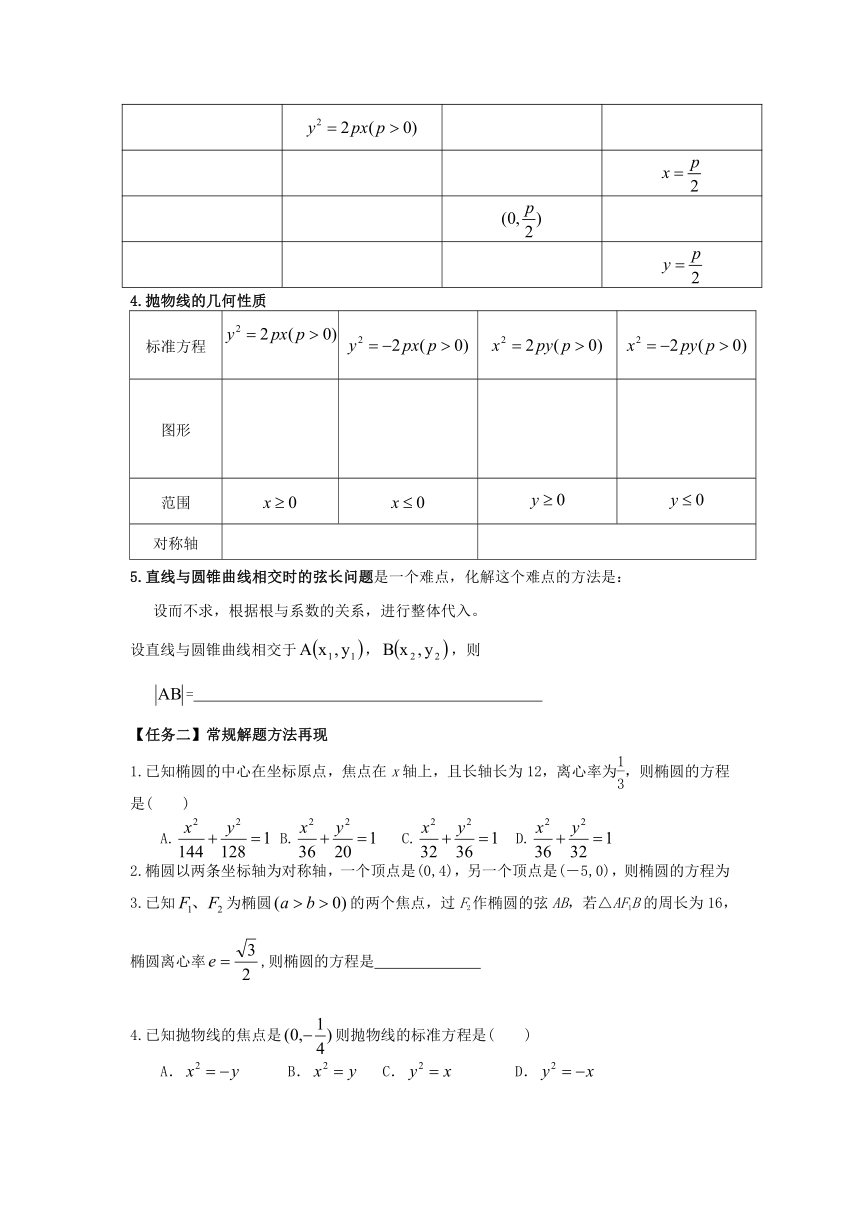
4.抛物线的几何性质
标准方程
图形
范围
对称轴
5.直线与圆锥曲线相交时的弦长问题是一个难点,化解这个难点的方法是:
设而不求,根据根与系数的关系,进行整体代入。
设直线与圆锥曲线相交于,,则
=
【任务二】常规解题方法再现
已知椭圆的中心在坐标原点,焦点在x轴上,且长轴长为12,离心率为,则椭圆的方程是( )
A. B. C. D.
2.椭圆以两条坐标轴为对称轴,一个顶点是(0,4),另一个顶点是(-5,0),则椭圆的方程为
3.已知为椭圆的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆离心率,则椭圆的方程是
4.已知抛物线的焦点是则抛物线的标准方程是( )
A. B. C. D.
5.以双曲线的上焦点为焦点的抛物线的方程为________.
6.若抛物线上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点的坐标
7.过椭圆的左焦点且倾角为的弦AB,求。
8.过椭圆的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,求△OAB的面积。
9.如果椭圆的弦被点平分,求这条弦所在的直线方程。
10.中心在原点,焦点坐标为(0, )的椭圆被直线截得的弦中点的横坐标为,求椭圆方程。
第三课时(仅供理科使用)
学习目标
理解直线与圆锥曲线位置关系的判断方式;
能够利用直线与圆锥曲线的位置关系进行综合应用;
3.学会挖掘几何关系,提升学生阅读分析的能力。
学习过程
【任务一】阅读例题
【范例1】如图,抛物线关于x轴对称,它的顶点在坐标原点,点,,均在抛物线上.
(1)写出该抛物线的方程及其准线方程;
(2)当与的斜率存在且倾斜角互补时,求的值 ( http: / / www.21cnjy.com )及直线AB的斜率.
( http: / / www.21cnjy.com )
仿例解题:已知抛物线上异于坐标原点的两个相异的动点,满足,问:的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
【范例2】已知椭圆中心在原点,焦点在轴上,一个顶点为,且其右焦点到直线的距离为,
(1)求椭圆的标准方程;(2)是否存在斜率为,且过定点的直线,使与椭圆交于不同的两个点,且?若存在,求出直线的方程;若不存在,说明理由。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )仿例解题:设直线与抛物线交于两点,已知当直线经过抛物线的焦点且与轴垂直时,的面积为(为坐标原点)。
(1)求抛物线的方程;(2)当直线经过点且与轴不垂直时,在轴上存在点,使得为正三角形,求的取值范围。
【任务二】阅读材料(选学)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
作业:
已知椭圆的中心是坐标原点,它的短轴长为,一个焦点的坐标为,一个定点的坐标为,且,过点的直线与椭圆相交于
求椭圆的方程及离心率;
如果,求直线的直线方程
第一课时
学习目标
1.理解直线与圆锥曲线位置关系的判断方法;
2.会判断已知直线和圆锥曲线的位置关系;
3.能够根据直线与圆锥曲线的位置关系求相应参数的取值范围;
学习过程
【任务一】阅读教材
阅读课本P67页例1、例2。仿照例题解法完成下面问题
仿照练习1:已知直线和椭圆,当取何值时,此直线与椭圆:(1)相交;(2)相切;(3)相离。
仿照练习2:已知直线与椭圆相交于不同的两点,求的取值范围。
【任务二】典型例题分析
例1:已知椭圆,弦的中点是,求弦所在的直线方程。
变式练习1:已知是直线被椭圆所截的线段的中点,求直线的方程。
例2:已知直线与双曲线相交于两点,是坐标原点,如果,求的值。
变式练习2:设抛物线与其过焦点的斜率为的直线相交于两点,是坐标原点,求的值。
作业:直线过点且与抛物线只有一个公共点,求直线的方程。
第二课时
学习目标
理解直线与圆锥曲线位置关系的判断方式;
能够根据根与系数的关系推导出弦长公式,并会应用弦长公式解决问题;
了解函数求最值的相关解决问题的方法。
学习过程
【任务一】阅读课本
阅读课本P68也例3.仿照例3的解法完成下面问题;
仿照练习:已知抛物线的弦过它的焦点,直线的斜率为2,求的长。
【任务二】典型例题分析
例1:已知斜率为的直线与抛物线相交于两点,如果线段的长等于,求直线的方程。
变式练习:已知抛物线的顶点在原点,对称轴是轴,它的弦所在直线的方程为,弦长等于,求抛物线的方程。
例2:已知直线与椭圆相交于两点,当变化时,求的最大值。
变式练习2:已知椭圆的离心率为,且经过点.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点的直线交椭圆于,两点,求△(为原点)面积的最大值。
第三课时
回顾有关圆锥曲线的几何性质以及标准方程;
能利用圆锥曲线的几何性质求相应圆锥曲线的标准方程;
熟练应用弦长公式以及中点坐标公式,掌握常规解决问题的方法。
学习过程
【任务一】基础知识巩固
1.椭圆的两个标准方程的几何性质与特征比较
焦点的位置 焦点在轴上 焦点在轴上
图形
标准方程
范围
顶点
轴长
焦点
焦距
对称性 对称轴: 对称中心:
离心率
2.双曲线的简单几何性质
标准方程
图形
几何性质 范围
焦点
顶点
对称轴 关于 对称,关于 对称
实虚轴长 实轴长为 ,虚轴长为
离心率
渐近线方程
3.抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
4.抛物线的几何性质
标准方程
图形
范围
对称轴
5.直线与圆锥曲线相交时的弦长问题是一个难点,化解这个难点的方法是:
设而不求,根据根与系数的关系,进行整体代入。
设直线与圆锥曲线相交于,,则
=
【任务二】常规解题方法再现
已知椭圆的中心在坐标原点,焦点在x轴上,且长轴长为12,离心率为,则椭圆的方程是( )
A. B. C. D.
2.椭圆以两条坐标轴为对称轴,一个顶点是(0,4),另一个顶点是(-5,0),则椭圆的方程为
3.已知为椭圆的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆离心率,则椭圆的方程是
4.已知抛物线的焦点是则抛物线的标准方程是( )
A. B. C. D.
5.以双曲线的上焦点为焦点的抛物线的方程为________.
6.若抛物线上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点的坐标
7.过椭圆的左焦点且倾角为的弦AB,求。
8.过椭圆的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,求△OAB的面积。
9.如果椭圆的弦被点平分,求这条弦所在的直线方程。
10.中心在原点,焦点坐标为(0, )的椭圆被直线截得的弦中点的横坐标为,求椭圆方程。
第三课时(仅供理科使用)
学习目标
理解直线与圆锥曲线位置关系的判断方式;
能够利用直线与圆锥曲线的位置关系进行综合应用;
3.学会挖掘几何关系,提升学生阅读分析的能力。
学习过程
【任务一】阅读例题
【范例1】如图,抛物线关于x轴对称,它的顶点在坐标原点,点,,均在抛物线上.
(1)写出该抛物线的方程及其准线方程;
(2)当与的斜率存在且倾斜角互补时,求的值 ( http: / / www.21cnjy.com )及直线AB的斜率.
( http: / / www.21cnjy.com )
仿例解题:已知抛物线上异于坐标原点的两个相异的动点,满足,问:的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
【范例2】已知椭圆中心在原点,焦点在轴上,一个顶点为,且其右焦点到直线的距离为,
(1)求椭圆的标准方程;(2)是否存在斜率为,且过定点的直线,使与椭圆交于不同的两个点,且?若存在,求出直线的方程;若不存在,说明理由。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )仿例解题:设直线与抛物线交于两点,已知当直线经过抛物线的焦点且与轴垂直时,的面积为(为坐标原点)。
(1)求抛物线的方程;(2)当直线经过点且与轴不垂直时,在轴上存在点,使得为正三角形,求的取值范围。
【任务二】阅读材料(选学)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
作业:
已知椭圆的中心是坐标原点,它的短轴长为,一个焦点的坐标为,一个定点的坐标为,且,过点的直线与椭圆相交于
求椭圆的方程及离心率;
如果,求直线的直线方程
