北师大版四年级下册数学《认识方程》单元结构化教学思考(课件)(共34张PPT)
文档属性
| 名称 | 北师大版四年级下册数学《认识方程》单元结构化教学思考(课件)(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-28 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
《认识方程》单元结构化教学思考
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
目 录
(一)学习内容分析
1.内容要求:
在新课标的要求中,方程属于数与代数领域第三学段(5、6年级)和第四学段(7-9年级)的内容。
第三学段属于数量关系主题下的内容要求是:根据情境理解等式的基本性质;在具体情境中,探索用字母表示事物的关系、性质、规律的方法,感悟用字母表示事物的一般性。
第四学段要求经历现实问题中量的分析,借助用字母表达的未知数,建立两个量之间关系的过程,知道方程是现实问题中含有未知数的等量关系的数学表达。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
(一)学习内容分析
2.学业要求:
第三学段(5、6年级)能在具体问题中感受等式的基本性质。能在具体情境中,用字母或含有字母的式子表示数量之间的关系、性质和规律,感悟用字母表示具有一般性。
第四学段(7-9年级)能根据具体问题中的数量关系列出方程,理解方程的意义;认识方程解的意义,经历估计方程解的过程;掌握等式的基本性质,能运用等式的基本性质进行等式的变形;能根据等式的基本性质解一元一次方程。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
(一)学习内容分析
1.结合具体情境,学会用字母表示数与数量关系,发展符号意识。
2.结合具体情境,体会等量关系,能用方程表示简单情境中的等量关系,了解方程的作用,发展模型意识。
3.了解等式的性质,能用等式的性质解简单的方程,发展推理意识,培养运算能力。
4.会用方程解决简单实际问题,进一步理解等量关系,发展应用意识。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
基于核心素养的教学目标:
符号意识
推理意识
模型意识
应用意识
运算能力
(一)学习内容分析
1.会用字母表示数与数量关系。
2.结合具体情境,能用方程表示等量关系。
3.利用等式的性质解方程。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
单元教学重点:
1.理解字母表示数的一般性。
2.结合具体情境,能用方程表示等量关系。
3.利用等式的性质解方程。
单元教学难点:
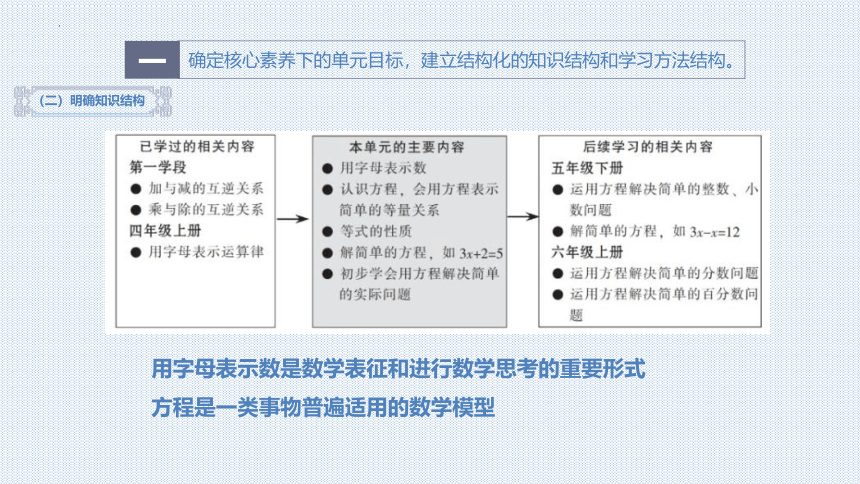
(二)明确知识结构
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
用字母表示数是数学表征和进行数学思考的重要形式
方程是一类事物普遍适用的数学模型
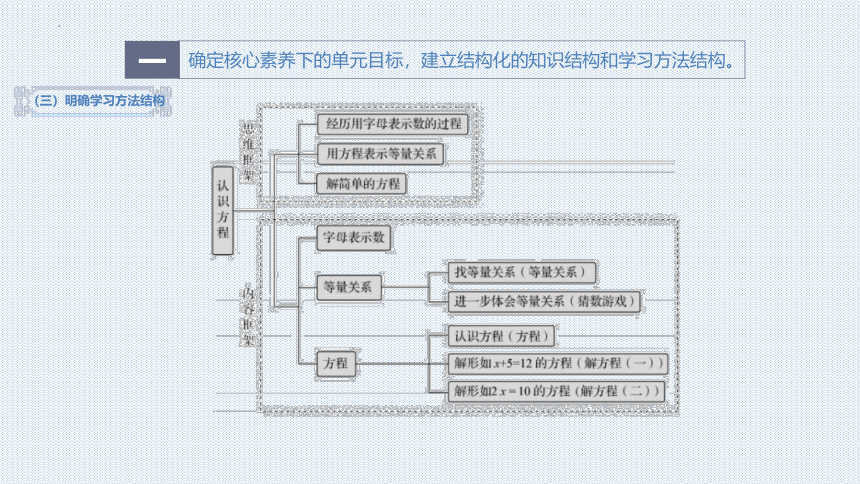
(三)明确学习方法结构
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
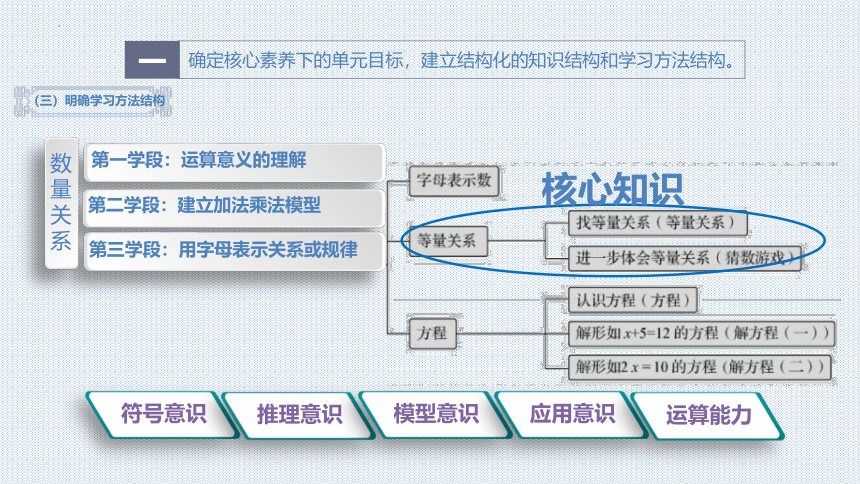
(三)明确学习方法结构
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
数量关系
第一学段:运算意义的理解
第二学段:建立加法乘法模型
第三学段:用字母表示关系或规律
核心知识
符号意识
推理意识
模型意识
应用意识
运算能力
学 情 分 析
二
目 录
学 情 分 析
二
学 生 已 有 基 础
有一定的算术知识。
已初步接融了一点代数知识。
不熟悉用等号将未知数与已知数联系起来这样的形式。
对字母参与运算并不熟悉。
不能很好地用数学语言表达等量关系。
学 生 存 在 问 题
学 情 分 析
二
第一,方程这一内容,学生最需要获得的到底是什么?
第二,基于这样的需要,我们该如何来教?
第三,要怎么判断学生是否已掌握方程思想?
学 情 分 析
二
第一,方程这一内容,学生最需要获得的到底是什么?
第二,基于这样的需要,我们该如何来教?
第三,要怎么判断学生是否已掌握方程思想?
结 合 课 例 具 体 分 析
三
目 录
列方程
解方程
应用
(一)字母表示数
教学目标
1.结合具体情境,会用字母表示数和数量关系、性质和规律,发展符号意识。
2.经历描述、抽象、概括的过程,感悟用字母表示数的一般性,发展推理意识。
(1)根据学情,是否需要把数青蛙的情境拆分开,先从一组关系开始入手。
(2)让学生经历思考、交流过程。明确数量关系的重要性。
(3)4×a既可以表示数量关系,也可以表示青蛙的腿数。
(一)字母表示数
教学目标
1.结合具体情境,会用字母表示数和数量关系、性质和规律,发展符号意识。
2.经历描述、抽象、概括的过程,感悟用字母表示数的一般性,发展推理意识。
4a还能解决哪些生活中的问题?
这些例子有什么共同点?
(二)等量关系
教学目标
1.结合具体情境,理解数学中的相等关系,会用式子表示等量关系,发展模型意识。
关键:
一是找相等关系。二是找相等的左右两边分别是什么?
天平里有没有相等关系?在哪里?
左边是什么?右边又是什么呢?
你能用文字和数学符号记录下来吗?
=
鹅的质量
2只鸭子和一只鸡的质量
(二)等量关系
教学目标
1.结合具体情境,理解数学中的相等关系,会用式子表示等量关系,发展模型意识。
两两一组出示,且不出示姚明身高226cm,直接出示妹妹说的话:姚明身高是我的2倍。
布置任务:你能用画一画、写一写的方法表示姚明与妹妹身高的关系吗?学生独立思考操作。
表示出正确的等量关系,有所标注
(二)等量关系
教学目标
1.结合具体情境,理解数学中的相等关系,会用式子表示等量关系,发展模型意识。
你能用含有文字的式子表示等量关系吗?
让学生解释等式两边分别表示什么意思。
模型是数量关系一般性的表达,是四则运算意义的抽象。本课教学中,经历找相等关系,用数学符号记录相等关系的过程,使学生经历了抽象、建模的过程,发展模型意识。
(三)认识方程
教学目标
1.结合具体情境,了解方程的意义,会根据等量关系列方程,发展模型意识、符号意识。
2.经历描述、抽象、概括,积累等量关系转化成方程的活动经验,发展推理意识。
突破列方程的难点在于:
学生各种各样不同的情境中,找题目中的等量关系,又怎样能帮助学生突破找等量关系的难点,引导学生变算术的思维为代数的思维。将未知量看成是一个量,与已知量之间建立联系,写出相等关系的式子,即把字母当成数字列算式。
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
每个天平的第二次状态一定要描述过程,而不是直接看结果。
不在于会背诵,在于通过天平平衡的过程,用数学的语言描述抽象等式的性质过程,发展推理意识,体会数学从一般到特殊的论证过程,也要对性质进一步理解。
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
利用等式性质解方程这个教学难点,方程解的过程一定也要结合图出发。
提问:为什么要减2呢?
通过教师连续追问和面向全体的“说一说”,让学生理解解方程的依据。
什么是方程的解?什么是解方程?
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
x-7
X=
12
x
x-7+7
12
7
解方程的过程培养学生运算能力,使学生能够明晰运算的对象和意义;将自然数的运算定律推广到简单字母符号的运算。
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
学生容易出现的问题,抛开了天平的情境,再图示、文字信息中找到等量关系,列方程并解方程。
列方程时学生容易写x=486+62,y=180-60-50这样的算数思维,我们要引导学生找到等量关系,列出方程,让学生说一说方程左右两边分别表示什么意思。
(五)《解方程(二)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质,会用等式的性质解ax=b类型的简单方程,培养应用意识和运算能力。
学生经历猜想-验证-应用的过程
注意描述天平变化的过程;举乘除法的例子进行不完全归纳。
利用等式性质解方程,结合教师追问和多媒体课件演示,让学生说清解方程的依据及每一步的等式两边的具体操作。
(五)《解方程(二)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质,会用等式的性质解ax=b类型的简单方程,培养应用意识和运算能力。
x
x÷3
9
x÷3×3
9
9
9
(六)《猜数游戏》
教学目标
1.在具体情境中,将稍复杂的ax±b=c方程转化成简单方程求解,培养运算能力,推理意识。
2.会用方程解决简单实际问题,培养应用意识。
3.知道检验方程的方法,能检验方程的解是否正确。
1.找关键词:比...多...、比...少、......的几倍是...、...等于....、...是...。
2.找到等量关系,设x,列方程解答。
(六)《猜数游戏》
教学目标
1.在具体情境中,将稍复杂的ax±b=c方程转化成简单方程求解,培养运算能力,推理意识。
2.会用方程解决简单实际问题,培养应用意识。
3.知道检验方程的方法,能检验方程的解是否正确。
淘气心中数是30,智慧老人心中数是淘气数的2倍再加20,智慧老人心中数是多少?
围绕此题讨论:算术解法与方程解法的区别在哪里?联系在哪里?哪一题更适合用方程来解?
让学生感知:列方程时,等量关系是不变的,也就是“天平”一直在那里。方程就是把未知的数量变成x,然后当作已知的条件去列式。列方程时,“已知数”和“未知数”都是有用的。
对于学生的难点是:算数方法和方程法的冲突。
(六)《猜数游戏》
教学目标
1.在具体情境中,将稍复杂的ax±b=c方程转化成简单方程求解,培养运算能力,推理意识。
2.会用方程解决简单实际问题,培养应用意识。
3.知道检验方程的方法,能检验方程的解是否正确。
解决ax±b=c的方程时,要先把ax看作一个整体,根据等式的性质把方程变成ax=c±b的形式,再等式两边÷a。重在让学生说清解方程过程。
把稍微复杂的方程转化成简单方程过程中,体现了化归思想,依据运算律将复杂方程简单化。
在本单元教学中,学生经历寻找规律-表达规律的过程,体会用字母表示数的一般性,发展符号意识;在结合情境建立模型,用字母表示等量关系的学习中经历了具体到抽象的过程,培养了模型意识。通过观察、描述、抽象过程总结出等式的基本性质,并利用等式基本性质解方程,落实了推理意识、应用意识、运算能力的核心素养。
第一,方程这一内容,学生最需要获得的到底是什么?
第二,基于这样的需要,我们该如何来教?
第三,要怎么判断学生是否已掌握方程思想?
要看学生列出来的方程,左边和右边是不是都是有意义且简单的描述。一种比较理想的做法是,学生在列出方程后,老师要进一步让他们来描述左边是什么,右边是什么,让他们自己体会到列的方程是不是个好的模型。如果发现方程左右两边的意义并不是很好描述,可以重新经历找相等关系、建立方程模型的过程。
本单元教学需注意
1.要鼓励学生用等式的性质解方程,而不是加减法各部分之间的关系。
2.遵循循序渐进的原则。
3.将“列”方程和“解”方程区别开来。
感 谢 聆 听
《认识方程》单元结构化教学思考
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
目 录
(一)学习内容分析
1.内容要求:
在新课标的要求中,方程属于数与代数领域第三学段(5、6年级)和第四学段(7-9年级)的内容。
第三学段属于数量关系主题下的内容要求是:根据情境理解等式的基本性质;在具体情境中,探索用字母表示事物的关系、性质、规律的方法,感悟用字母表示事物的一般性。
第四学段要求经历现实问题中量的分析,借助用字母表达的未知数,建立两个量之间关系的过程,知道方程是现实问题中含有未知数的等量关系的数学表达。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
(一)学习内容分析
2.学业要求:
第三学段(5、6年级)能在具体问题中感受等式的基本性质。能在具体情境中,用字母或含有字母的式子表示数量之间的关系、性质和规律,感悟用字母表示具有一般性。
第四学段(7-9年级)能根据具体问题中的数量关系列出方程,理解方程的意义;认识方程解的意义,经历估计方程解的过程;掌握等式的基本性质,能运用等式的基本性质进行等式的变形;能根据等式的基本性质解一元一次方程。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
(一)学习内容分析
1.结合具体情境,学会用字母表示数与数量关系,发展符号意识。
2.结合具体情境,体会等量关系,能用方程表示简单情境中的等量关系,了解方程的作用,发展模型意识。
3.了解等式的性质,能用等式的性质解简单的方程,发展推理意识,培养运算能力。
4.会用方程解决简单实际问题,进一步理解等量关系,发展应用意识。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
基于核心素养的教学目标:
符号意识
推理意识
模型意识
应用意识
运算能力
(一)学习内容分析
1.会用字母表示数与数量关系。
2.结合具体情境,能用方程表示等量关系。
3.利用等式的性质解方程。
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
单元教学重点:
1.理解字母表示数的一般性。
2.结合具体情境,能用方程表示等量关系。
3.利用等式的性质解方程。
单元教学难点:
(二)明确知识结构
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
用字母表示数是数学表征和进行数学思考的重要形式
方程是一类事物普遍适用的数学模型
(三)明确学习方法结构
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
(三)明确学习方法结构
确定核心素养下的单元目标,建立结构化的知识结构和学习方法结构。
一
数量关系
第一学段:运算意义的理解
第二学段:建立加法乘法模型
第三学段:用字母表示关系或规律
核心知识
符号意识
推理意识
模型意识
应用意识
运算能力
学 情 分 析
二
目 录
学 情 分 析
二
学 生 已 有 基 础
有一定的算术知识。
已初步接融了一点代数知识。
不熟悉用等号将未知数与已知数联系起来这样的形式。
对字母参与运算并不熟悉。
不能很好地用数学语言表达等量关系。
学 生 存 在 问 题
学 情 分 析
二
第一,方程这一内容,学生最需要获得的到底是什么?
第二,基于这样的需要,我们该如何来教?
第三,要怎么判断学生是否已掌握方程思想?
学 情 分 析
二
第一,方程这一内容,学生最需要获得的到底是什么?
第二,基于这样的需要,我们该如何来教?
第三,要怎么判断学生是否已掌握方程思想?
结 合 课 例 具 体 分 析
三
目 录
列方程
解方程
应用
(一)字母表示数
教学目标
1.结合具体情境,会用字母表示数和数量关系、性质和规律,发展符号意识。
2.经历描述、抽象、概括的过程,感悟用字母表示数的一般性,发展推理意识。
(1)根据学情,是否需要把数青蛙的情境拆分开,先从一组关系开始入手。
(2)让学生经历思考、交流过程。明确数量关系的重要性。
(3)4×a既可以表示数量关系,也可以表示青蛙的腿数。
(一)字母表示数
教学目标
1.结合具体情境,会用字母表示数和数量关系、性质和规律,发展符号意识。
2.经历描述、抽象、概括的过程,感悟用字母表示数的一般性,发展推理意识。
4a还能解决哪些生活中的问题?
这些例子有什么共同点?
(二)等量关系
教学目标
1.结合具体情境,理解数学中的相等关系,会用式子表示等量关系,发展模型意识。
关键:
一是找相等关系。二是找相等的左右两边分别是什么?
天平里有没有相等关系?在哪里?
左边是什么?右边又是什么呢?
你能用文字和数学符号记录下来吗?
=
鹅的质量
2只鸭子和一只鸡的质量
(二)等量关系
教学目标
1.结合具体情境,理解数学中的相等关系,会用式子表示等量关系,发展模型意识。
两两一组出示,且不出示姚明身高226cm,直接出示妹妹说的话:姚明身高是我的2倍。
布置任务:你能用画一画、写一写的方法表示姚明与妹妹身高的关系吗?学生独立思考操作。
表示出正确的等量关系,有所标注
(二)等量关系
教学目标
1.结合具体情境,理解数学中的相等关系,会用式子表示等量关系,发展模型意识。
你能用含有文字的式子表示等量关系吗?
让学生解释等式两边分别表示什么意思。
模型是数量关系一般性的表达,是四则运算意义的抽象。本课教学中,经历找相等关系,用数学符号记录相等关系的过程,使学生经历了抽象、建模的过程,发展模型意识。
(三)认识方程
教学目标
1.结合具体情境,了解方程的意义,会根据等量关系列方程,发展模型意识、符号意识。
2.经历描述、抽象、概括,积累等量关系转化成方程的活动经验,发展推理意识。
突破列方程的难点在于:
学生各种各样不同的情境中,找题目中的等量关系,又怎样能帮助学生突破找等量关系的难点,引导学生变算术的思维为代数的思维。将未知量看成是一个量,与已知量之间建立联系,写出相等关系的式子,即把字母当成数字列算式。
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
每个天平的第二次状态一定要描述过程,而不是直接看结果。
不在于会背诵,在于通过天平平衡的过程,用数学的语言描述抽象等式的性质过程,发展推理意识,体会数学从一般到特殊的论证过程,也要对性质进一步理解。
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
利用等式性质解方程这个教学难点,方程解的过程一定也要结合图出发。
提问:为什么要减2呢?
通过教师连续追问和面向全体的“说一说”,让学生理解解方程的依据。
什么是方程的解?什么是解方程?
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
x-7
X=
12
x
x-7+7
12
7
解方程的过程培养学生运算能力,使学生能够明晰运算的对象和意义;将自然数的运算定律推广到简单字母符号的运算。
(四)《解方程(一)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质、“方程解”的意义,会用等式的性质解x±a=b类型的简单方程,培养应用意识和运算能力。
学生容易出现的问题,抛开了天平的情境,再图示、文字信息中找到等量关系,列方程并解方程。
列方程时学生容易写x=486+62,y=180-60-50这样的算数思维,我们要引导学生找到等量关系,列出方程,让学生说一说方程左右两边分别表示什么意思。
(五)《解方程(二)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质,会用等式的性质解ax=b类型的简单方程,培养应用意识和运算能力。
学生经历猜想-验证-应用的过程
注意描述天平变化的过程;举乘除法的例子进行不完全归纳。
利用等式性质解方程,结合教师追问和多媒体课件演示,让学生说清解方程的依据及每一步的等式两边的具体操作。
(五)《解方程(二)》
教学目标
1.通过观察天平变化的具体情境,类比、抽象得到等式的性质,发展推理能力。
2.理解等式的性质,会用等式的性质解ax=b类型的简单方程,培养应用意识和运算能力。
x
x÷3
9
x÷3×3
9
9
9
(六)《猜数游戏》
教学目标
1.在具体情境中,将稍复杂的ax±b=c方程转化成简单方程求解,培养运算能力,推理意识。
2.会用方程解决简单实际问题,培养应用意识。
3.知道检验方程的方法,能检验方程的解是否正确。
1.找关键词:比...多...、比...少、......的几倍是...、...等于....、...是...。
2.找到等量关系,设x,列方程解答。
(六)《猜数游戏》
教学目标
1.在具体情境中,将稍复杂的ax±b=c方程转化成简单方程求解,培养运算能力,推理意识。
2.会用方程解决简单实际问题,培养应用意识。
3.知道检验方程的方法,能检验方程的解是否正确。
淘气心中数是30,智慧老人心中数是淘气数的2倍再加20,智慧老人心中数是多少?
围绕此题讨论:算术解法与方程解法的区别在哪里?联系在哪里?哪一题更适合用方程来解?
让学生感知:列方程时,等量关系是不变的,也就是“天平”一直在那里。方程就是把未知的数量变成x,然后当作已知的条件去列式。列方程时,“已知数”和“未知数”都是有用的。
对于学生的难点是:算数方法和方程法的冲突。
(六)《猜数游戏》
教学目标
1.在具体情境中,将稍复杂的ax±b=c方程转化成简单方程求解,培养运算能力,推理意识。
2.会用方程解决简单实际问题,培养应用意识。
3.知道检验方程的方法,能检验方程的解是否正确。
解决ax±b=c的方程时,要先把ax看作一个整体,根据等式的性质把方程变成ax=c±b的形式,再等式两边÷a。重在让学生说清解方程过程。
把稍微复杂的方程转化成简单方程过程中,体现了化归思想,依据运算律将复杂方程简单化。
在本单元教学中,学生经历寻找规律-表达规律的过程,体会用字母表示数的一般性,发展符号意识;在结合情境建立模型,用字母表示等量关系的学习中经历了具体到抽象的过程,培养了模型意识。通过观察、描述、抽象过程总结出等式的基本性质,并利用等式基本性质解方程,落实了推理意识、应用意识、运算能力的核心素养。
第一,方程这一内容,学生最需要获得的到底是什么?
第二,基于这样的需要,我们该如何来教?
第三,要怎么判断学生是否已掌握方程思想?
要看学生列出来的方程,左边和右边是不是都是有意义且简单的描述。一种比较理想的做法是,学生在列出方程后,老师要进一步让他们来描述左边是什么,右边是什么,让他们自己体会到列的方程是不是个好的模型。如果发现方程左右两边的意义并不是很好描述,可以重新经历找相等关系、建立方程模型的过程。
本单元教学需注意
1.要鼓励学生用等式的性质解方程,而不是加减法各部分之间的关系。
2.遵循循序渐进的原则。
3.将“列”方程和“解”方程区别开来。
感 谢 聆 听
