冀教版六年级上册数学6.2 比例尺(课件)(共39张PPT)
文档属性
| 名称 | 冀教版六年级上册数学6.2 比例尺(课件)(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-28 00:00:00 | ||
图片预览










文档简介
(共39张PPT)
6.2比例尺
■考点一 按1∶1画图的含义
第 1 课时 比例尺的意义
1.含义:画出的图形与要求的尺寸一样,我们就说这样的图是按1 : 1画的。
2.特征:按1:1画出的图形和原图完全一样 ,既没有放大,也没有缩小。
例 1 下面不是按1:1画出左图画片的是( )。
第 1 课时 比例尺的意义
第 1 课时 比例尺的意义
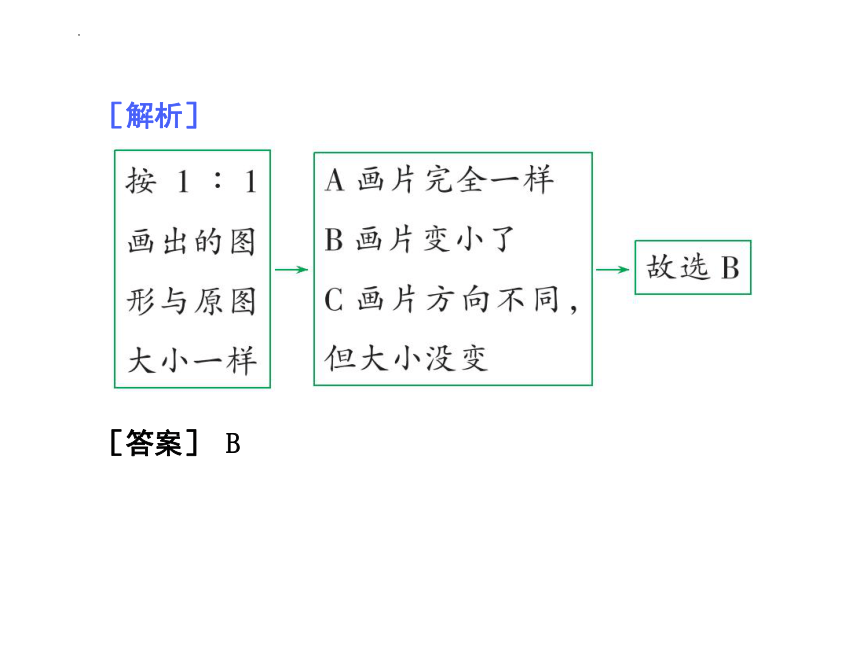
[解析]
[答案] B
■考点二 认识比例尺
第 1 课时 比例尺的意义
1.一幅图的图上距离与实际距离的比,就是这幅图的比例尺。如图上1厘米表示实际长度10 厘米,我们就说这幅图的比例尺是 1 : 10。
2.比例尺的书写规则:比的前项写1,表示图上1厘米;后项写几,表示图上1厘米代表实际的厘米数。
3.如果一个比例尺的后项为 1,说明这个比例尺是放大比例尺。如2:1就是用图上2厘米表示实际长度1厘米,是把原图放大后画出来的。
第 1 课时 比例尺的意义
重难突破
比例尺可以带单位吗
答:不能。比例尺是图上距离与实际距离的比,表示的是两个数的关系,不是具体数值,所以不能带单位。
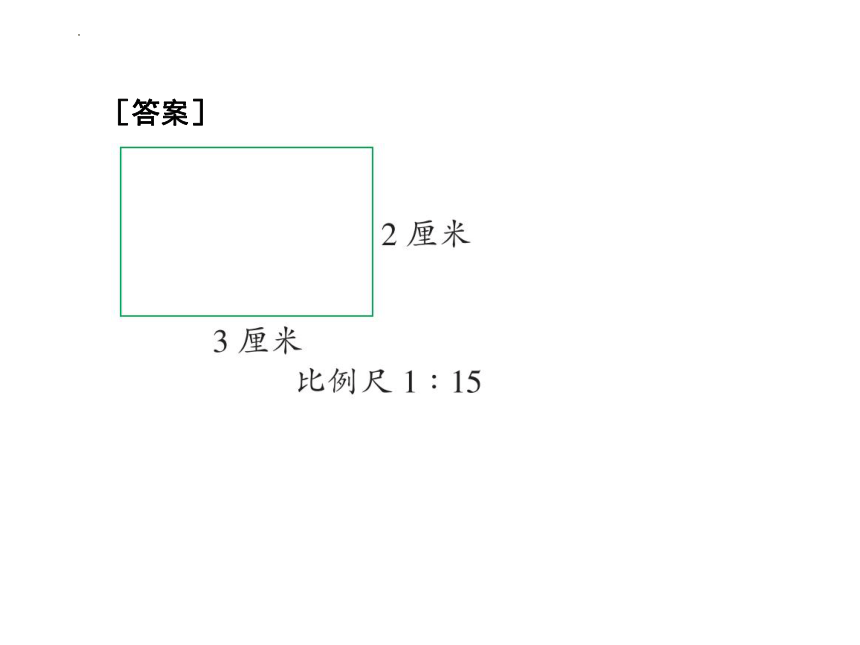
例 2 小亮想画一个长45厘米、宽30厘米的镜框示意图,可在练习本上根本画不下,后来他按1:15的比例尺画了这个图,你能画出小亮画的镜框示意图吗
第 1 课时 比例尺的意义
[解析]
第 1 课时 比例尺的意义
[答案]
第 1 课时 比例尺的意义
■易错易混分析 误认为比例尺的前项都是1
第 1 课时 比例尺的意义
例 3 所有比例尺的前项一定都是1。 ( )
[解析]缩小比例尺的前项一般是1,但放大比例尺的前项却不一定是1。
[答案] ×
易错警示:通常缩小比例尺的前项为1,放大比例尺的后项为1。
■考点一 比例尺的意义及简单应用
第 2 课时 比例尺的应用
1.比例尺的书写形式:图上距离:实际距离=比例尺或
=比例尺。
2.比例尺的实质:比例尺实质上一个比,前项表示图上距离,后项表示实际距离,比例尺的后面不能带单位名称。
3.给出比例尺和图上距离求实际距离时,根据“实际距离=图上距离÷比例尺”求实际距离。
4.给出比例尺和实际距离求图上距离时,根据“图上距离=实际距离×比例尺”求图上距离。
第 2 课时 比例尺的应用
重难突破
为什么可以用除法计算实际距离
答:因为 =比例尺,图上距离相当于比的前项,实际距离相当于比的后项,求实际距离就是求比的后项,所以可以用“实际距离=图上距离÷比例尺”来计算。
例 1 小明家和奶奶家相距120 米,画在一幅地图上的距离是3厘米,求这幅地图的比例尺。
第 2 课时 比例尺的应用
第 2 课时 比例尺的应用
[解析] 比例尺=图上距离:实际距离
3厘米 120米
[答案] 3厘米:120米=3厘米: 12000厘米=1 : 4000
答:这幅地图的比例尺是1 : 4000。
例 2 下面是育英小学的平面图,你能计算出学校的实际的长和宽各是多少米吗
第 2 课时 比例尺的应用
第 2 课时 比例尺的应用
[解析] 测量出育英小学平面图上的长为6厘米,宽为4厘米。
第 2 课时 比例尺的应用
[答案] 图上长:6厘米
实际长:6÷ =12000(厘米)=120(米)
图上宽:4厘米
实际宽:4÷ =8000(厘米) =80(米)
答:学校的实际的长是120米,宽是80米。
■考点二 比例尺的复杂应用
第 2 课时 比例尺的应用
遇到一些数值特别大的比例尺时,可以先把比例尺转化成1厘米表示实际距离多少千米,再根据测量的图上距离,相乘求出两地的实际距离。在生活中我们可以根据地图上的比例尺对两地的实际距离进行估测。
例 3 在比例尺是1:3000000的地图上,量得 A地到B地的距离约为4.5 厘米,那么A地到B地的实际距离大约是多少千米
第 2 课时 比例尺的应用
[解析]实际距离=图上距离÷比例尺
4.5厘米 1:3000000
第 2 课时 比例尺的应用
[答案] 方法一:4.5÷ = 13500000(厘米)=135(千米)
方法二:3000000厘米=30千米
30×4.5=135(千米)
答:A地到B地的实际距离大约是135千米。
例 4 甲、乙两地的实际距离约为120千米,在比例尺是 1:2000000 的地图上,甲地到乙地的距离大约是多少厘米
第 2 课时 比例尺的应用
[解析]图上距离=实际距离×比例尺
120千米
第 2 课时 比例尺的应用
[答案] 120千米=12000000厘米
12000000× =6(厘米)
答:甲地到乙地的距离大约是6厘米。
■易错易混分析 求比例尺时忽略了统一单位
第 2 课时 比例尺的应用
例 5 在一幅地图上,10厘米的线段表示500千米的实际距离,这幅地图的比例尺是( )。
[解析]比例尺=图上距离∶实际距离=10厘米∶500千米=10厘米∶50000000厘米=1∶5000000。
[答案] 1∶5000000
易错警示:图上距离一般用厘米作单位,实际距离一般用米或千米作单位,计算时要先统一单位。
■考点一 线段比例尺的认识
第 3 课时 线段比例尺
1.用一条标有数量的线段来表示和地面上相对应的实际距离的比例尺,就是线段比例尺,如: 。以前学习的比例尺是用数字形式表示的,就是数值比例尺,如:1:500。
2.线段比例尺和数值比例尺的转化:根据线段比例尺,写出图上距离和实际距离的比,统一单位后再化成最简单的整数比的形式。
第 3 课时 线段比例尺
重难突破
线段比例尺和数值比例尺转化时,需要注意什么
答:(1)转化的计算过程要统一单位。
(2)线段比例尺上有单位,但改写成数值比例尺时,后面一定不能带单位。
例 1 一幅地图的比例尺是1 : 3000000你能用线段比例尺表示出来吗 。
第 3 课时 线段比例尺
[解析] 比例尺为1 : 3000000
图上1厘米代表实际距离30千米
[答案]
■考点二 线段比例尺的应用
第 3 课时 线段比例尺
例 2 量一量,算一算。
亮亮家和火车站的实际距离是多少米
[解析]
第 3 课时 线段比例尺
[答案] 500×2=1000(米)
答:亮亮家和火车站的实际距离是1000米。
例 3 一辆汽车正在向正南方向行驶。从下图看,城市甲在汽车( )方向, 与汽车的实际距离是( )千米。
第 3 课时 线段比例尺
[解析]
第 3 课时 线段比例尺
第 3 课时 线段比例尺
[答案] 南偏西45° 50
■易错易混分析 混淆数值比例尺和线段比例尺
第 3 课时 线段比例尺
例 4 比例尺 和比例尺1∶20表示的意义相同。 ( )
[解析]两个比例尺都有20,但表示的意义不相同。线段比例尺是用图上1厘米的距离表示实际距离20千米,而1∶20是用图上1厘米的距离表示实际距离20厘米。
[答案] ×
易错警示:要想判断线段比例尺和数值比例尺所表示的意义是否相同,要先把它们化成相同形式的比例尺,再进行判断。
■考点 用比例尺解决问题
第 4 课时 用比例尺解决问题
1.设计游览路线时,先要明确各景点的位置,再根据比例尺计算出相邻两个景点的实际距离,最后根据要求确定游览路线。
2.根据所给平面图计算实际面积,首先要借助直尺测量出图上距离,然后再根据比例尺求出实际距离,最后根据相应形状的面积公式计算出实际面积。
例 1 下面是公园的平面图,算一算,全部游览完至少要走多少米
第 4 课时 用比例尺解决问题
第 4 课时 用比例尺解决问题
[解析]
第 4 课时 用比例尺解决问题
[答案] 20×1=20(米) 20×3=60(米)
20×5=100(米) 20×2.5=50(米)
20×3=60(米)
20+60+100+50+60=290(米)
答:全部游览完至少要走290米。
例 2 算一算,旱冰场的实际占地面积是多少平方米
第 4 课时 用比例尺解决问题
第 4 课时 用比例尺解决问题
[解析]
第 4 课时 用比例尺解决问题
[答案] 测量得出图中的旱冰场长2.5厘米,宽1.5厘米。
2.5÷ =5000(厘米)=50(米)
1.5÷ =3000(厘米)=30(米)
50×30=1500(平方米)
答:旱冰场的实际占地面积是1500平方米。
6.2比例尺
■考点一 按1∶1画图的含义
第 1 课时 比例尺的意义
1.含义:画出的图形与要求的尺寸一样,我们就说这样的图是按1 : 1画的。
2.特征:按1:1画出的图形和原图完全一样 ,既没有放大,也没有缩小。
例 1 下面不是按1:1画出左图画片的是( )。
第 1 课时 比例尺的意义
第 1 课时 比例尺的意义
[解析]
[答案] B
■考点二 认识比例尺
第 1 课时 比例尺的意义
1.一幅图的图上距离与实际距离的比,就是这幅图的比例尺。如图上1厘米表示实际长度10 厘米,我们就说这幅图的比例尺是 1 : 10。
2.比例尺的书写规则:比的前项写1,表示图上1厘米;后项写几,表示图上1厘米代表实际的厘米数。
3.如果一个比例尺的后项为 1,说明这个比例尺是放大比例尺。如2:1就是用图上2厘米表示实际长度1厘米,是把原图放大后画出来的。
第 1 课时 比例尺的意义
重难突破
比例尺可以带单位吗
答:不能。比例尺是图上距离与实际距离的比,表示的是两个数的关系,不是具体数值,所以不能带单位。
例 2 小亮想画一个长45厘米、宽30厘米的镜框示意图,可在练习本上根本画不下,后来他按1:15的比例尺画了这个图,你能画出小亮画的镜框示意图吗
第 1 课时 比例尺的意义
[解析]
第 1 课时 比例尺的意义
[答案]
第 1 课时 比例尺的意义
■易错易混分析 误认为比例尺的前项都是1
第 1 课时 比例尺的意义
例 3 所有比例尺的前项一定都是1。 ( )
[解析]缩小比例尺的前项一般是1,但放大比例尺的前项却不一定是1。
[答案] ×
易错警示:通常缩小比例尺的前项为1,放大比例尺的后项为1。
■考点一 比例尺的意义及简单应用
第 2 课时 比例尺的应用
1.比例尺的书写形式:图上距离:实际距离=比例尺或
=比例尺。
2.比例尺的实质:比例尺实质上一个比,前项表示图上距离,后项表示实际距离,比例尺的后面不能带单位名称。
3.给出比例尺和图上距离求实际距离时,根据“实际距离=图上距离÷比例尺”求实际距离。
4.给出比例尺和实际距离求图上距离时,根据“图上距离=实际距离×比例尺”求图上距离。
第 2 课时 比例尺的应用
重难突破
为什么可以用除法计算实际距离
答:因为 =比例尺,图上距离相当于比的前项,实际距离相当于比的后项,求实际距离就是求比的后项,所以可以用“实际距离=图上距离÷比例尺”来计算。
例 1 小明家和奶奶家相距120 米,画在一幅地图上的距离是3厘米,求这幅地图的比例尺。
第 2 课时 比例尺的应用
第 2 课时 比例尺的应用
[解析] 比例尺=图上距离:实际距离
3厘米 120米
[答案] 3厘米:120米=3厘米: 12000厘米=1 : 4000
答:这幅地图的比例尺是1 : 4000。
例 2 下面是育英小学的平面图,你能计算出学校的实际的长和宽各是多少米吗
第 2 课时 比例尺的应用
第 2 课时 比例尺的应用
[解析] 测量出育英小学平面图上的长为6厘米,宽为4厘米。
第 2 课时 比例尺的应用
[答案] 图上长:6厘米
实际长:6÷ =12000(厘米)=120(米)
图上宽:4厘米
实际宽:4÷ =8000(厘米) =80(米)
答:学校的实际的长是120米,宽是80米。
■考点二 比例尺的复杂应用
第 2 课时 比例尺的应用
遇到一些数值特别大的比例尺时,可以先把比例尺转化成1厘米表示实际距离多少千米,再根据测量的图上距离,相乘求出两地的实际距离。在生活中我们可以根据地图上的比例尺对两地的实际距离进行估测。
例 3 在比例尺是1:3000000的地图上,量得 A地到B地的距离约为4.5 厘米,那么A地到B地的实际距离大约是多少千米
第 2 课时 比例尺的应用
[解析]实际距离=图上距离÷比例尺
4.5厘米 1:3000000
第 2 课时 比例尺的应用
[答案] 方法一:4.5÷ = 13500000(厘米)=135(千米)
方法二:3000000厘米=30千米
30×4.5=135(千米)
答:A地到B地的实际距离大约是135千米。
例 4 甲、乙两地的实际距离约为120千米,在比例尺是 1:2000000 的地图上,甲地到乙地的距离大约是多少厘米
第 2 课时 比例尺的应用
[解析]图上距离=实际距离×比例尺
120千米
第 2 课时 比例尺的应用
[答案] 120千米=12000000厘米
12000000× =6(厘米)
答:甲地到乙地的距离大约是6厘米。
■易错易混分析 求比例尺时忽略了统一单位
第 2 课时 比例尺的应用
例 5 在一幅地图上,10厘米的线段表示500千米的实际距离,这幅地图的比例尺是( )。
[解析]比例尺=图上距离∶实际距离=10厘米∶500千米=10厘米∶50000000厘米=1∶5000000。
[答案] 1∶5000000
易错警示:图上距离一般用厘米作单位,实际距离一般用米或千米作单位,计算时要先统一单位。
■考点一 线段比例尺的认识
第 3 课时 线段比例尺
1.用一条标有数量的线段来表示和地面上相对应的实际距离的比例尺,就是线段比例尺,如: 。以前学习的比例尺是用数字形式表示的,就是数值比例尺,如:1:500。
2.线段比例尺和数值比例尺的转化:根据线段比例尺,写出图上距离和实际距离的比,统一单位后再化成最简单的整数比的形式。
第 3 课时 线段比例尺
重难突破
线段比例尺和数值比例尺转化时,需要注意什么
答:(1)转化的计算过程要统一单位。
(2)线段比例尺上有单位,但改写成数值比例尺时,后面一定不能带单位。
例 1 一幅地图的比例尺是1 : 3000000你能用线段比例尺表示出来吗 。
第 3 课时 线段比例尺
[解析] 比例尺为1 : 3000000
图上1厘米代表实际距离30千米
[答案]
■考点二 线段比例尺的应用
第 3 课时 线段比例尺
例 2 量一量,算一算。
亮亮家和火车站的实际距离是多少米
[解析]
第 3 课时 线段比例尺
[答案] 500×2=1000(米)
答:亮亮家和火车站的实际距离是1000米。
例 3 一辆汽车正在向正南方向行驶。从下图看,城市甲在汽车( )方向, 与汽车的实际距离是( )千米。
第 3 课时 线段比例尺
[解析]
第 3 课时 线段比例尺
第 3 课时 线段比例尺
[答案] 南偏西45° 50
■易错易混分析 混淆数值比例尺和线段比例尺
第 3 课时 线段比例尺
例 4 比例尺 和比例尺1∶20表示的意义相同。 ( )
[解析]两个比例尺都有20,但表示的意义不相同。线段比例尺是用图上1厘米的距离表示实际距离20千米,而1∶20是用图上1厘米的距离表示实际距离20厘米。
[答案] ×
易错警示:要想判断线段比例尺和数值比例尺所表示的意义是否相同,要先把它们化成相同形式的比例尺,再进行判断。
■考点 用比例尺解决问题
第 4 课时 用比例尺解决问题
1.设计游览路线时,先要明确各景点的位置,再根据比例尺计算出相邻两个景点的实际距离,最后根据要求确定游览路线。
2.根据所给平面图计算实际面积,首先要借助直尺测量出图上距离,然后再根据比例尺求出实际距离,最后根据相应形状的面积公式计算出实际面积。
例 1 下面是公园的平面图,算一算,全部游览完至少要走多少米
第 4 课时 用比例尺解决问题
第 4 课时 用比例尺解决问题
[解析]
第 4 课时 用比例尺解决问题
[答案] 20×1=20(米) 20×3=60(米)
20×5=100(米) 20×2.5=50(米)
20×3=60(米)
20+60+100+50+60=290(米)
答:全部游览完至少要走290米。
例 2 算一算,旱冰场的实际占地面积是多少平方米
第 4 课时 用比例尺解决问题
第 4 课时 用比例尺解决问题
[解析]
第 4 课时 用比例尺解决问题
[答案] 测量得出图中的旱冰场长2.5厘米,宽1.5厘米。
2.5÷ =5000(厘米)=50(米)
1.5÷ =3000(厘米)=30(米)
50×30=1500(平方米)
答:旱冰场的实际占地面积是1500平方米。
