河南省信阳高级中学北湖校区2024-2025学年高二(上)开学数学试卷(含答案)
文档属性
| 名称 | 河南省信阳高级中学北湖校区2024-2025学年高二(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 68.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-28 10:13:29 | ||
图片预览



文档简介
2024-2025学年河南省信阳高级中学北湖校区高二(上)开学数学试卷
一、单选题:本题共7小题,每小题5分,共35分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,平行四边形是水平放置的一个平面图形的直观图,其中,,,则原图形与间的距离为( )
A.
B.
C.
D.
2.为了得到函数的图象,只要把函数图象上所有的点( )
A. 向左平移个单位长度 B. 向右平移个单位长度
C. 向左平移个单位长度 D. 向右平移个单位长度
3.已知函数的定义域为,则函数的定义域为( )
A. B.
C. D.
4.直线:与:平行,则实数的值是( )
A. 或 B. C. 或 D.
5.已知,,是三个非零平面向量,则下列叙述正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
6.已知,是两条不同的直线,,是两个不重合的平面,则有下列命题
,,;
,,;
,,;
,.
其中正确命题的个数为( )
A. B. C. D.
7.在三棱锥中,线段上的点满足,线段上的点满足,则三棱锥
和三棱锥的体积之比为( )
A. B. C. D.
二、多选题:本题共5小题,共30分。在每小题给出的选项中,有多项符合题目要求。
8.已知为虚数单位,则( )
A. 若复数的共轭复数为,则
B. 若,,则的充要条件是
C. 若复数,则,
D. 若复数,则
9.已知,,且,则( )
A. B.
C. D.
10.下列说法不正确的有( )
A. 若两条直线与互相平行,则实数的值为
B. 若直线不经过第三象限,则在第二象限
C. 过点且在两坐标轴上的截距相等的直线的方程为
D. 已知直线和以,为端点的线段相交,则实数的取值范围为或
11.中,角,,所对的边为,,,下列叙述正确的是( )
A. 若,则是等腰三角形
B. 若,则一定是等边三角形
C. 若,则
D. 若,则
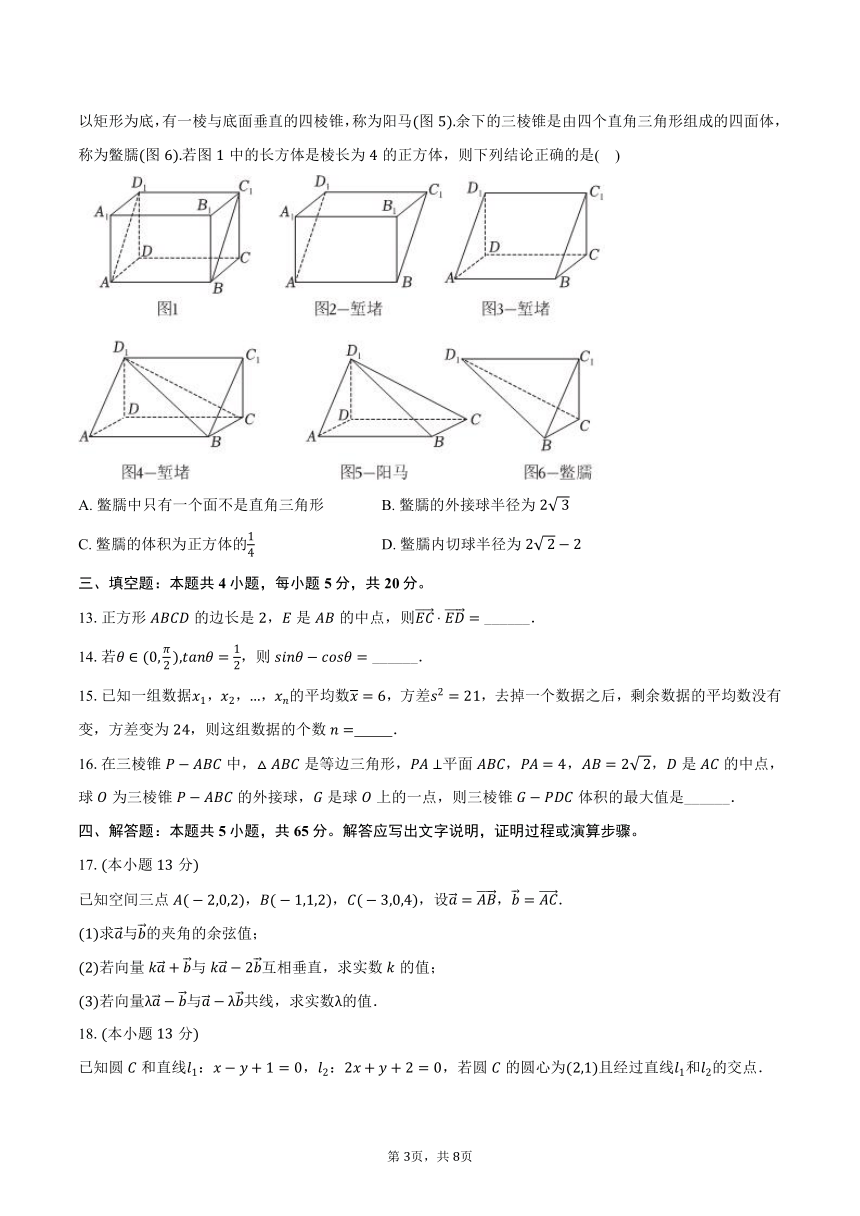
12.阳马和鳖臑是我国古代对一些特殊锥体的称谓,取一长方体按下图斜割一分为二,得两个一模一样的三棱柱图,图,称为堑堵再沿堑堵的一顶点与相对的棱剖开图,得四棱锥和三棱锥各一个以矩形为底,有一棱与底面垂直的四棱锥,称为阳马图余下的三棱锥是由四个直角三角形组成的四面体,称为鳖臑图若图中的长方体是棱长为的正方体,则下列结论正确的是( )
A. 鳖臑中只有一个面不是直角三角形 B. 鳖臑的外接球半径为
C. 鳖臑的体积为正方体的 D. 鳖臑内切球半径为
三、填空题:本题共4小题,每小题5分,共20分。
13.正方形的边长是,是的中点,则 ______.
14.若,则 ______.
15.已知一组数据,,,的平均数,方差,去掉一个数据之后,剩余数据的平均数没有变,方差变为,则这组数据的个数 .
16.在三棱锥中,是等边三角形,平面,,,是的中点,球为三棱锥的外接球,是球上的一点,则三棱锥体积的最大值是______.
四、解答题:本题共5小题,共65分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知空间三点,,,设,.
求与的夹角的余弦值;
若向量与互相垂直,求实数的值;
若向量与共线,求实数的值.
18.本小题分
已知圆和直线:,:,若圆的圆心为且经过直线和的交点.
Ⅰ求圆的标准方程;
Ⅱ直线:与圆交于,两点,且,求直线的方程.
19.本小题分
在中,内角,,的对边分别是,,,且.
求角的大小;
若,且的面积为,求边上的中线长.
20.本小题分
如图,三棱锥中,,,,为中点.
证明;
点满足,求二面角的正弦值.
21.本小题分
作为世界乒坛本赛季收官战,首届世界乒乓球职业大联盟世界杯总决赛年月日在新加坡结束男女单打决赛的较量,国乒包揽双冠成为最大赢家我市男子乒乓球队为备战下届市运会,在某训练基地进行封闭式训练,甲、乙两位队员进行对抗赛,每局依次轮流发球,连续赢个球者获胜,通过分析甲、乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响,已知某局甲先发球.
求该局打个球甲赢的概率;
求该局打个球结束的概率.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:空间三点,,,,.
,,
设与的夹角为,
则.
,,
,
,
向量与互相垂直,
,
整理,得,
解得实数的值为或.
,,
,
,
向量与共线,
,解得实数的值为或.
18.解:Ⅰ联立,解得,
故直线和的交点为,
,
故圆的标准方程为;
Ⅱ直线:与圆交于,两点,且,
则,解得,
故直线的方程为.
19.解:,由正弦定理得:,
因为,所以,
故,即,
因为,所以,故,
所以,所以.
在中,由余弦定理,得,
因为,所以,
所以,
设的中点为,则,
两边同时平方得:,
所以,
即边上的中线长为.
20.证明:连接,,
,为中点.
,
又,,
与均为等边三角形,
,
,,
平面,
平面,
.
解:设,
,
,,
,
,
又,,
平面,
以为原点,建立如图所示空间直角坐标系,
,,,,
,
,
,,,
设平面与平面的一个法向量分别为,,
则,令,解得,
,令,解得,,
故,,
设二面角的平面角为,
则,
故,
所以二面角的正弦值为.
21.解:设甲发球甲赢为事件,乙发球甲赢为事件,该局打个球甲赢为事件,
由题知,,,,
,
该局打个球甲赢的概率为.
设该局打个球结束时甲赢为事件,乙赢为事件,打个球结束为事件,易知,为互斥事件,
,,,
,
,
,
该局打个球结束的概率为.
第1页,共1页
一、单选题:本题共7小题,每小题5分,共35分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,平行四边形是水平放置的一个平面图形的直观图,其中,,,则原图形与间的距离为( )
A.
B.
C.
D.
2.为了得到函数的图象,只要把函数图象上所有的点( )
A. 向左平移个单位长度 B. 向右平移个单位长度
C. 向左平移个单位长度 D. 向右平移个单位长度
3.已知函数的定义域为,则函数的定义域为( )
A. B.
C. D.
4.直线:与:平行,则实数的值是( )
A. 或 B. C. 或 D.
5.已知,,是三个非零平面向量,则下列叙述正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
6.已知,是两条不同的直线,,是两个不重合的平面,则有下列命题
,,;
,,;
,,;
,.
其中正确命题的个数为( )
A. B. C. D.
7.在三棱锥中,线段上的点满足,线段上的点满足,则三棱锥
和三棱锥的体积之比为( )
A. B. C. D.
二、多选题:本题共5小题,共30分。在每小题给出的选项中,有多项符合题目要求。
8.已知为虚数单位,则( )
A. 若复数的共轭复数为,则
B. 若,,则的充要条件是
C. 若复数,则,
D. 若复数,则
9.已知,,且,则( )
A. B.
C. D.
10.下列说法不正确的有( )
A. 若两条直线与互相平行,则实数的值为
B. 若直线不经过第三象限,则在第二象限
C. 过点且在两坐标轴上的截距相等的直线的方程为
D. 已知直线和以,为端点的线段相交,则实数的取值范围为或
11.中,角,,所对的边为,,,下列叙述正确的是( )
A. 若,则是等腰三角形
B. 若,则一定是等边三角形
C. 若,则
D. 若,则
12.阳马和鳖臑是我国古代对一些特殊锥体的称谓,取一长方体按下图斜割一分为二,得两个一模一样的三棱柱图,图,称为堑堵再沿堑堵的一顶点与相对的棱剖开图,得四棱锥和三棱锥各一个以矩形为底,有一棱与底面垂直的四棱锥,称为阳马图余下的三棱锥是由四个直角三角形组成的四面体,称为鳖臑图若图中的长方体是棱长为的正方体,则下列结论正确的是( )
A. 鳖臑中只有一个面不是直角三角形 B. 鳖臑的外接球半径为
C. 鳖臑的体积为正方体的 D. 鳖臑内切球半径为
三、填空题:本题共4小题,每小题5分,共20分。
13.正方形的边长是,是的中点,则 ______.
14.若,则 ______.
15.已知一组数据,,,的平均数,方差,去掉一个数据之后,剩余数据的平均数没有变,方差变为,则这组数据的个数 .
16.在三棱锥中,是等边三角形,平面,,,是的中点,球为三棱锥的外接球,是球上的一点,则三棱锥体积的最大值是______.
四、解答题:本题共5小题,共65分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知空间三点,,,设,.
求与的夹角的余弦值;
若向量与互相垂直,求实数的值;
若向量与共线,求实数的值.
18.本小题分
已知圆和直线:,:,若圆的圆心为且经过直线和的交点.
Ⅰ求圆的标准方程;
Ⅱ直线:与圆交于,两点,且,求直线的方程.
19.本小题分
在中,内角,,的对边分别是,,,且.
求角的大小;
若,且的面积为,求边上的中线长.
20.本小题分
如图,三棱锥中,,,,为中点.
证明;
点满足,求二面角的正弦值.
21.本小题分
作为世界乒坛本赛季收官战,首届世界乒乓球职业大联盟世界杯总决赛年月日在新加坡结束男女单打决赛的较量,国乒包揽双冠成为最大赢家我市男子乒乓球队为备战下届市运会,在某训练基地进行封闭式训练,甲、乙两位队员进行对抗赛,每局依次轮流发球,连续赢个球者获胜,通过分析甲、乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响,已知某局甲先发球.
求该局打个球甲赢的概率;
求该局打个球结束的概率.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:空间三点,,,,.
,,
设与的夹角为,
则.
,,
,
,
向量与互相垂直,
,
整理,得,
解得实数的值为或.
,,
,
,
向量与共线,
,解得实数的值为或.
18.解:Ⅰ联立,解得,
故直线和的交点为,
,
故圆的标准方程为;
Ⅱ直线:与圆交于,两点,且,
则,解得,
故直线的方程为.
19.解:,由正弦定理得:,
因为,所以,
故,即,
因为,所以,故,
所以,所以.
在中,由余弦定理,得,
因为,所以,
所以,
设的中点为,则,
两边同时平方得:,
所以,
即边上的中线长为.
20.证明:连接,,
,为中点.
,
又,,
与均为等边三角形,
,
,,
平面,
平面,
.
解:设,
,
,,
,
,
又,,
平面,
以为原点,建立如图所示空间直角坐标系,
,,,,
,
,
,,,
设平面与平面的一个法向量分别为,,
则,令,解得,
,令,解得,,
故,,
设二面角的平面角为,
则,
故,
所以二面角的正弦值为.
21.解:设甲发球甲赢为事件,乙发球甲赢为事件,该局打个球甲赢为事件,
由题知,,,,
,
该局打个球甲赢的概率为.
设该局打个球结束时甲赢为事件,乙赢为事件,打个球结束为事件,易知,为互斥事件,
,,,
,
,
,
该局打个球结束的概率为.
第1页,共1页
同课章节目录
