初中数学人教版九年级上册 第22章 二次函数 章末复习教案(表格式)
文档属性
| 名称 | 初中数学人教版九年级上册 第22章 二次函数 章末复习教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 105.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 00:00:00 | ||
图片预览

文档简介
义务教育学校课时教案
备课时间: 上课时间:
课题 章末复习 主备人
教学目标 1.掌握本章重要的知识点,能用相关函数知识解决具体问题.2.通过梳理本章知识,回顾解决实际问题中所涉及数形结合思想、方程思想、分类讨论思想的过程,加深对本章知识的理解.3.在利用本章知识解决具体问题过程中,进一步增强数学应用意识,感受数学的应用价值,激发学习兴趣.
核心素养 思维能力:通过对不同类型的二次函数问题进行分析和解决,锻炼逻辑思维、抽象思维和逆向思维等,能够从复杂的问题中找到关键信息,运用合适的方法解决问题。
运算能力:在求解二次函数的顶点、对称轴、与坐标轴的交点,以及运用待定系数法求解析式等过程中,都需要进行精确的数学运算。
空间观念:在根据二次函数的解析式想象其图像的形状、开口方向、对称轴位置等方面,需要具备一定的空间想象能力。模型观念:将实际问题转化为二次函数的数学模型,明确变量之间的关系,构建函数表达式。这需要学生能够提取关键信息,简化实际情境,建立数学结构。
数据观念:对实际问题中的数据进行分析和处理,确定自变量和因变量的取值范围,以及函数的最值等情况,从而为解决问题提供依据。
德育渗透 课堂中通过学生画二次函数的图像,让学生感受抛物线的对称美、和谐美,可以让学生在生活中寻找对称美,数学美。课堂中结合当时情境,遇上“国庆节、中秋节”,课堂中可以穿插知识,让同学们感受中国传统文化,更要传承中华传统美德,弘扬“社会主义核心价值观”。
教学重点 本章知识结构梳理及其应用.
教学难点 灵活运用二次函数性质解决实际问题.
学情分析
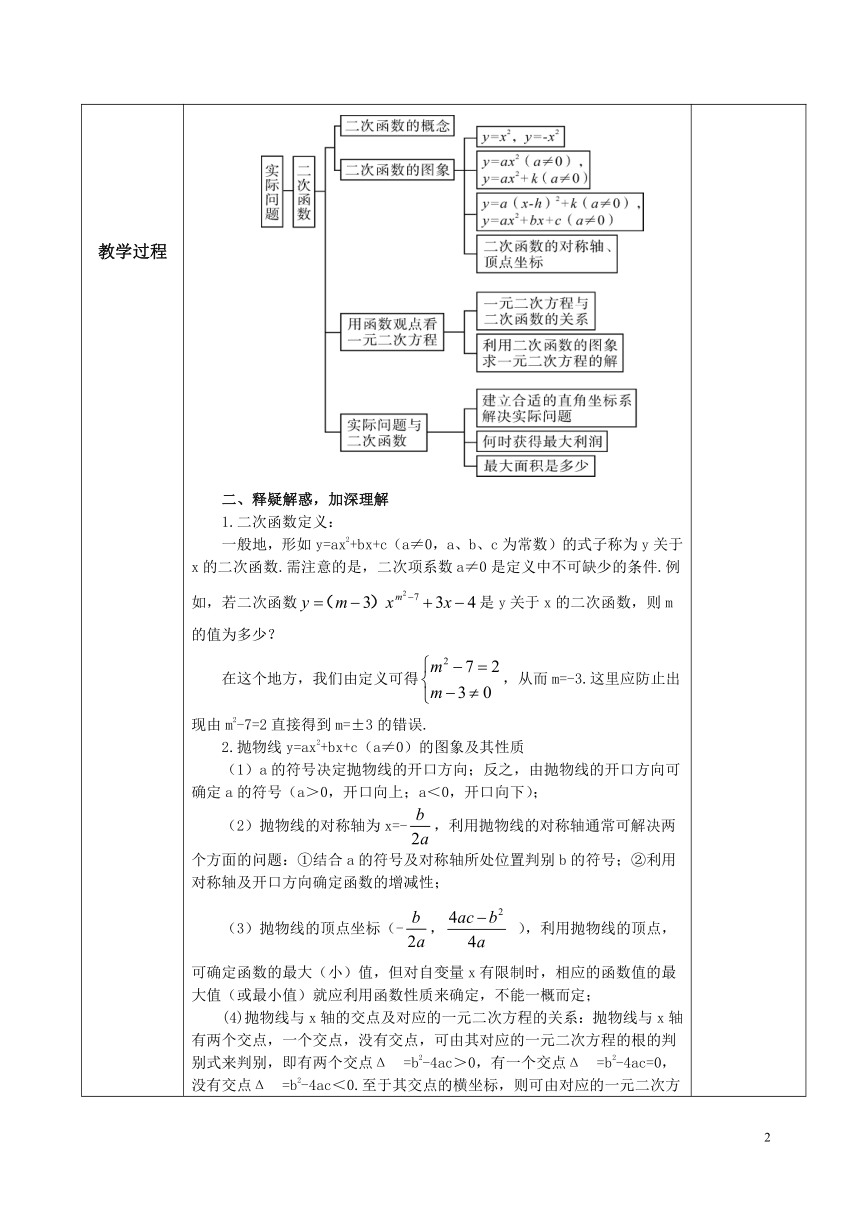
教学过程 一、知识框图,整体把握二、释疑解惑,加深理解1.二次函数定义:一般地,形如y=ax2+bx+c(a≠0,a、b、c为常数)的式子称为y关于x的二次函数.需注意的是,二次项系数a≠0是定义中不可缺少的条件.例如,若二次函数是y关于x的二次函数,则m的值为多少?在这个地方,我们由定义可得,从而m=-3.这里应防止出现由m2-7=2直接得到m=±3的错误.2.抛物线y=ax2+bx+c(a≠0)的图象及其性质(1)a的符号决定抛物线的开口方向;反之,由抛物线的开口方向可确定a的符号(a>0,开口向上;a<0,开口向下);(2)抛物线的对称轴为x=-,利用抛物线的对称轴通常可解决两个方面的问题:①结合a的符号及对称轴所处位置判别b的符号;②利用对称轴及开口方向确定函数的增减性;(3)抛物线的顶点坐标(-, ),利用抛物线的顶点,可确定函数的最大(小)值,但对自变量x有限制时,相应的函数值的最大值(或最小值)就应利用函数性质来确定,不能一概而定;(4)抛物线与x轴的交点及对应的一元二次方程的关系:抛物线与x轴有两个交点,一个交点,没有交点,可由其对应的一元二次方程的根的判别式来判别,即有两个交点?Δ=b2-4ac>0,有一个交点?Δ=b2-4ac=0,没有交点?Δ=b2-4ac<0.至于其交点的横坐标,则可由对应的一元二次方程得到.三、典例精析,复习新知例1已知二次函数的图象如图所示,现有下列结论:①b2-4ac>0,②a>0,③b>0,④c>0,⑤9a+3b+c<0,则其中结论正确的个数是( )A.2个 B.3个 C.4个 D.5个【解析】由开口方向可知②a>0正确,结合对称轴x=1>0,即->0,可知b<0,故③错;又抛物线与x轴有两个交点,有Δ=b2-4ac>0,从而①正确;而抛物线交y轴于负半轴,因此c<0;利用抛物线的对称性知,抛物线与x轴的另一个交点应在3~4之间,故当x=3时,y=9a+3b+c<0,因而结论正确的个数有3个,应选B.需注意的是,在判别9a+3b+c<0时,由抛物线的对称轴为x=1及抛物线的对称性,得到当x=3和x=-1时,它们的函数值应相同,从而作出正确判别.例2已知二次函数y=x2+bx+c,其图象对称轴为x=1,且经过(2, ).(1)求此二次函数的表达式;(2)该图象与x轴交于B、C两点(B点在C点左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC的面积最大,并求出最大面积.【分析】在(1)中,由对称轴x=1,可得到关于b的方程,从而可得二次函数表达式;在(2)中,一方面应利用解方程方法得到B、C点坐标,再结合图象知,当E点处于此抛物线的顶点时,S△EBC最大,可得结论.例3某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:(1)求y与x之间的函数关系式;(2)若该商品的销售单价在45元~70元之间浮动,①销售单价定为多少元时,销售利润最大?此时销售量为多少?②商场想要在这段时间内获得4550元的销售利润,销售单价应定为多少?【分析】在(2)中,可先得到销售利润w(元)与销售单价x之间的函数关系式为w=y·(x-25),再结合函数性质及自变量范围是45≤x≤70可得①的结论,并通过解方程,获得②的结论.需要注意的是,本例中“销售单价在45元~70元之间浮动”已暗含着自变量x的取值是受限制的,因而确定销售利润的最大值及求获得4550元利润时,销售单价是多少时,一定应结合函数图象,利用函数性质作出合理说明,不可轻下结论.【教学说明】师生共同回顾本章主要知识点,教师适时给予评讲,阐明应用各知识点时需注意哪些问题,加深学生理解.对于所选例题,既可让学生自主完成,也可合作交流获得结论,根据需要可适当增减例题,对所选例题,教师应给予诱导,适时点拨,达到巩固所学知识的目的.四、师生互动,课堂小结1.通过这节课的学习你有哪些问题?2.回顾本章知识,你还有哪些问题?【教学说明】学生相互交流,进一步加深对本章知识的理解,针对学生存在的疑问,可当堂解决,也可课后个别辅导,帮助他(她)完善对本章知识的认知. 二次备课
板书设计 章末复习 概念练习1练习2
作业设计与布置 作业类型 作业内容 试做时长
基础性作业 基本性作业(必做)
鼓励性作业(选择)
挑战性作业(选择)
拓展性作业
作业反馈记录
教学反思
备课组长审核签字 教研组长审核签字 年级部审核签字 党支部审核签字
时间 时间 时间 时间
备课时间: 上课时间:
课题 章末复习 主备人
教学目标 1.掌握本章重要的知识点,能用相关函数知识解决具体问题.2.通过梳理本章知识,回顾解决实际问题中所涉及数形结合思想、方程思想、分类讨论思想的过程,加深对本章知识的理解.3.在利用本章知识解决具体问题过程中,进一步增强数学应用意识,感受数学的应用价值,激发学习兴趣.
核心素养 思维能力:通过对不同类型的二次函数问题进行分析和解决,锻炼逻辑思维、抽象思维和逆向思维等,能够从复杂的问题中找到关键信息,运用合适的方法解决问题。
运算能力:在求解二次函数的顶点、对称轴、与坐标轴的交点,以及运用待定系数法求解析式等过程中,都需要进行精确的数学运算。
空间观念:在根据二次函数的解析式想象其图像的形状、开口方向、对称轴位置等方面,需要具备一定的空间想象能力。模型观念:将实际问题转化为二次函数的数学模型,明确变量之间的关系,构建函数表达式。这需要学生能够提取关键信息,简化实际情境,建立数学结构。
数据观念:对实际问题中的数据进行分析和处理,确定自变量和因变量的取值范围,以及函数的最值等情况,从而为解决问题提供依据。
德育渗透 课堂中通过学生画二次函数的图像,让学生感受抛物线的对称美、和谐美,可以让学生在生活中寻找对称美,数学美。课堂中结合当时情境,遇上“国庆节、中秋节”,课堂中可以穿插知识,让同学们感受中国传统文化,更要传承中华传统美德,弘扬“社会主义核心价值观”。
教学重点 本章知识结构梳理及其应用.
教学难点 灵活运用二次函数性质解决实际问题.
学情分析
教学过程 一、知识框图,整体把握二、释疑解惑,加深理解1.二次函数定义:一般地,形如y=ax2+bx+c(a≠0,a、b、c为常数)的式子称为y关于x的二次函数.需注意的是,二次项系数a≠0是定义中不可缺少的条件.例如,若二次函数是y关于x的二次函数,则m的值为多少?在这个地方,我们由定义可得,从而m=-3.这里应防止出现由m2-7=2直接得到m=±3的错误.2.抛物线y=ax2+bx+c(a≠0)的图象及其性质(1)a的符号决定抛物线的开口方向;反之,由抛物线的开口方向可确定a的符号(a>0,开口向上;a<0,开口向下);(2)抛物线的对称轴为x=-,利用抛物线的对称轴通常可解决两个方面的问题:①结合a的符号及对称轴所处位置判别b的符号;②利用对称轴及开口方向确定函数的增减性;(3)抛物线的顶点坐标(-, ),利用抛物线的顶点,可确定函数的最大(小)值,但对自变量x有限制时,相应的函数值的最大值(或最小值)就应利用函数性质来确定,不能一概而定;(4)抛物线与x轴的交点及对应的一元二次方程的关系:抛物线与x轴有两个交点,一个交点,没有交点,可由其对应的一元二次方程的根的判别式来判别,即有两个交点?Δ=b2-4ac>0,有一个交点?Δ=b2-4ac=0,没有交点?Δ=b2-4ac<0.至于其交点的横坐标,则可由对应的一元二次方程得到.三、典例精析,复习新知例1已知二次函数的图象如图所示,现有下列结论:①b2-4ac>0,②a>0,③b>0,④c>0,⑤9a+3b+c<0,则其中结论正确的个数是( )A.2个 B.3个 C.4个 D.5个【解析】由开口方向可知②a>0正确,结合对称轴x=1>0,即->0,可知b<0,故③错;又抛物线与x轴有两个交点,有Δ=b2-4ac>0,从而①正确;而抛物线交y轴于负半轴,因此c<0;利用抛物线的对称性知,抛物线与x轴的另一个交点应在3~4之间,故当x=3时,y=9a+3b+c<0,因而结论正确的个数有3个,应选B.需注意的是,在判别9a+3b+c<0时,由抛物线的对称轴为x=1及抛物线的对称性,得到当x=3和x=-1时,它们的函数值应相同,从而作出正确判别.例2已知二次函数y=x2+bx+c,其图象对称轴为x=1,且经过(2, ).(1)求此二次函数的表达式;(2)该图象与x轴交于B、C两点(B点在C点左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC的面积最大,并求出最大面积.【分析】在(1)中,由对称轴x=1,可得到关于b的方程,从而可得二次函数表达式;在(2)中,一方面应利用解方程方法得到B、C点坐标,再结合图象知,当E点处于此抛物线的顶点时,S△EBC最大,可得结论.例3某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:(1)求y与x之间的函数关系式;(2)若该商品的销售单价在45元~70元之间浮动,①销售单价定为多少元时,销售利润最大?此时销售量为多少?②商场想要在这段时间内获得4550元的销售利润,销售单价应定为多少?【分析】在(2)中,可先得到销售利润w(元)与销售单价x之间的函数关系式为w=y·(x-25),再结合函数性质及自变量范围是45≤x≤70可得①的结论,并通过解方程,获得②的结论.需要注意的是,本例中“销售单价在45元~70元之间浮动”已暗含着自变量x的取值是受限制的,因而确定销售利润的最大值及求获得4550元利润时,销售单价是多少时,一定应结合函数图象,利用函数性质作出合理说明,不可轻下结论.【教学说明】师生共同回顾本章主要知识点,教师适时给予评讲,阐明应用各知识点时需注意哪些问题,加深学生理解.对于所选例题,既可让学生自主完成,也可合作交流获得结论,根据需要可适当增减例题,对所选例题,教师应给予诱导,适时点拨,达到巩固所学知识的目的.四、师生互动,课堂小结1.通过这节课的学习你有哪些问题?2.回顾本章知识,你还有哪些问题?【教学说明】学生相互交流,进一步加深对本章知识的理解,针对学生存在的疑问,可当堂解决,也可课后个别辅导,帮助他(她)完善对本章知识的认知. 二次备课
板书设计 章末复习 概念练习1练习2
作业设计与布置 作业类型 作业内容 试做时长
基础性作业 基本性作业(必做)
鼓励性作业(选择)
挑战性作业(选择)
拓展性作业
作业反馈记录
教学反思
备课组长审核签字 教研组长审核签字 年级部审核签字 党支部审核签字
时间 时间 时间 时间
同课章节目录
