2024-2025学年山东省济南市槐荫区西城实验学校八年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年山东省济南市槐荫区西城实验学校八年级(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-28 00:00:00 | ||
图片预览




文档简介
2024-2025学年山东省济南市槐荫区西城实验学校八年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )
A. B. C. D.
2.下列长度的三条线段能组成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
3.某细菌的直径为毫米,数据用科学记数法表示为( )
A. B. C. D.
4.下列命题中的真命题是( )
A. 相等的角是对顶角 B. 若两个角的和为,则这两个角互补
C. 若,满足,则 D. 同位角相等
5.星期天,小王去朋友家借书,下图是他离家的距离千米与时间分钟的函数图象,根据图象信息,下列说法正确的是( )
A. 小王去时的速度大于回家的速度
B. 小王在朋友家停留了分钟
C. 小王去时所花的时间少于回家所花的时间
D. 小王去时走上坡路,回家时走下坡路
6.的三个内角::::,则这个三角形是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 等腰三角形
7.下列各式能用平方差公式计算的是( )
A. B.
C. D.
8.如图,≌,若,则的长度为( )
A.
B.
C.
D.
9.如图,直线,,,则( )
A.
B.
C.
D.
10.如图,在锐角三角形中,直线为的中垂线,射线为的角平分线,且直线与射线相交于点若,,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题4分,共24分。
11.计算: ______.
12.如图,是的中线,是边上的中点,连接,若的面积为,则的面积为______.
13.有一棵树苗,刚栽下去时树高为米,以后每年长米,则树高米与年数年之间的关系式为______.
14.如图,把一张长方形纸片沿折叠后,、分别在、的位置上,与的交点为,若,则______.
15.如图,在下列网格中,小正方形的边长均为,点、、都在格点上,则的度数为______.
16.如图,在中,,,线段,的垂直平分线交于点,则的长度为______.
三、解答题:本题共10小题,共80分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算;
化简:.
18.本小题分
计算:先化简,再求值:,其中,.
19.本小题分
如图,、为直角,与相交于点,,求证:推理过程请注明理由
20.本小题分
如图,点、分别在、上,于点,,,求证:.
证明:因为已知,
所以 ______
又因为已知,
所以______同位角相等,两直线平行,
所以______,
所以 ______
又因为 ______平角的定义
所以 ______,
又因为已知,
所以______,
所以______
21.本小题分
甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离开城的距离千米与甲车行驶的时间小时之间的函数关系如图所示,则下列结论:
在上述变化过程中,自变量是______,因变量是______;
,两城相距______千米;
乙车比甲车晚出发______小时,______填甲车或乙车先到达城;
乙车出发______后小时追上甲车;
当甲、乙两车相距千米时,______.
22.本小题分
如图,在长为,宽为的长方形铁片上,挖去长为,宽为的小长方形铁片.
计算剩余部分即阴影部分的面积;
求出当,时的阴影面积.
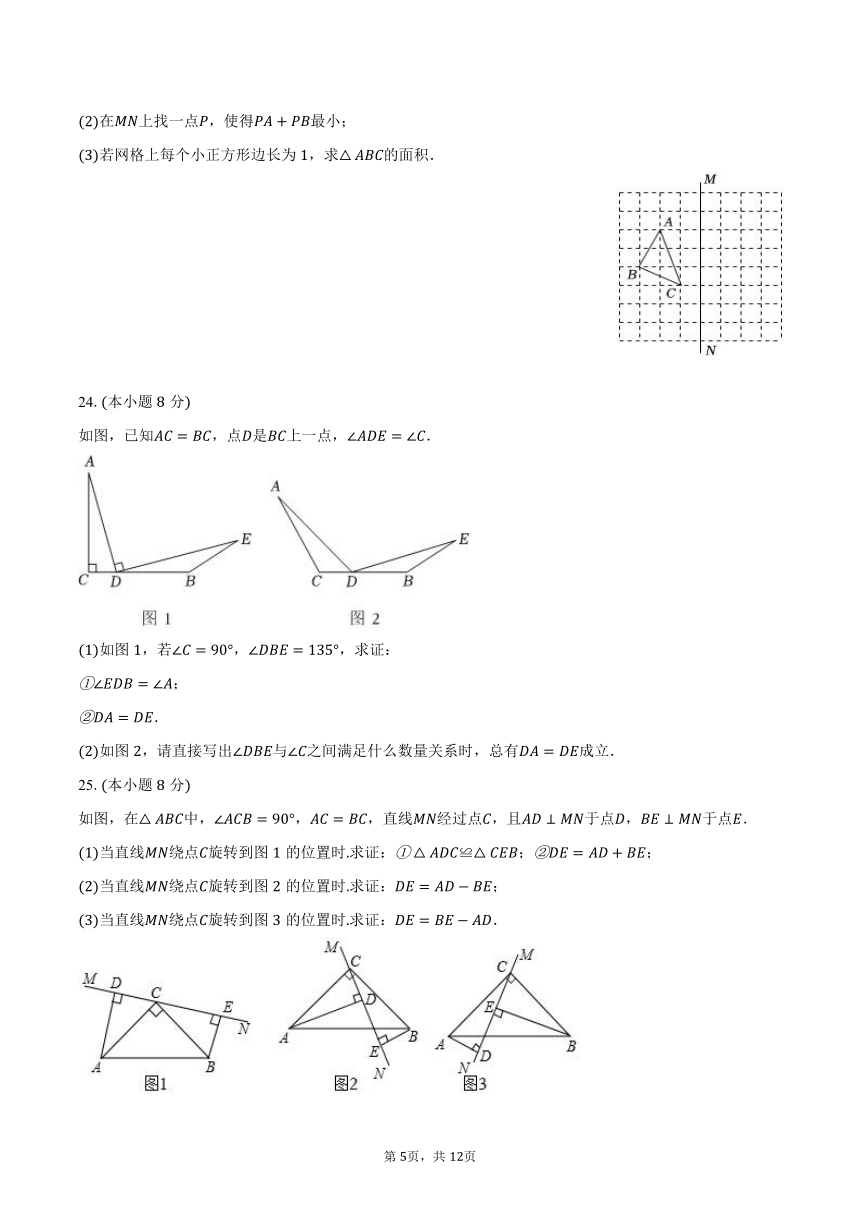
23.本小题分
如图所示,在正方形网格上有一个.
作关于直线的对称图形不写作法;
在上找一点,使得最小;
若网格上每个小正方形边长为,求的面积.
24.本小题分
如图,已知,点是上一点,.
如图,若,,求证:
;
.
如图,请直接写出与之间满足什么数量关系时,总有成立.
25.本小题分
如图,在中,,,直线经过点,且于点,于点.
当直线绕点旋转到图的位置时求证:≌;;
当直线绕点旋转到图的位置时求证:;
当直线绕点旋转到图的位置时求证:.
26.本小题分
如图,在等边中,边厘米,若动点从点开始,按的路径运动,且速度为厘米秒,设点的运动时间为秒.
当时,判断与的位置关系,并说明理由;
当的面积为面积的一半时,求的值;
另有一点,从点开始,按的路径运动,且速度为厘米秒,若、两点同时出发,当、中有一点到达终点时,另一点也停止运动.当为何值时,直线把的周长分成相等的两部分.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:
;
.
18.解:原式
,
当,时,
原式
.
19.证明:、为直角,
,
在和中,
,
≌,
.
20.证明:因为已知,
所以.
又因为已知,
所以同位角相等,两直线平行,
所以两直线平行,同位角相等,
所以
又因为平角的定义
所以,
又因为已知,
所以同角的余角相等,
所以内错角相等,两直线平行
21.甲车行驶的时间;两车离开城的距离;
;
;乙;
;
或或或.
22.解:根据题意可得,
;
,时,
原式.
23.解:如图所示,即为所求;
连接交于,点即为所求;
.
24.证明:,
,
;
在上截取,连接,如图,
,
,
,
,
,即:,
由知:,
在和中,
,
≌,
;
解:当时,总有成立.理由如下:
如图,在上截取,连接,
在上截取,
,
,
,,,
,
,
,
当时,,
≌,
.
25.证明:,
,而于,于,
,,
,
在和中,
,
≌,
由知≌,
,,
;
,
.
,
≌,
,,
.
,
.
,
≌,
,,
.
26.解:判断:,
理由如下:如图,
,
,
,
;
当的面积为面积的一半时,点为中点或点为中点,则或,
或,
当的面积为面积的一半时,的值为或;
当点在边上,且点在边上时,,
则,
,
当点在边上,且点在边上时,,,
则,
,
所以当为或秒时,直线把的周长分成相等的两部分.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )
A. B. C. D.
2.下列长度的三条线段能组成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
3.某细菌的直径为毫米,数据用科学记数法表示为( )
A. B. C. D.
4.下列命题中的真命题是( )
A. 相等的角是对顶角 B. 若两个角的和为,则这两个角互补
C. 若,满足,则 D. 同位角相等
5.星期天,小王去朋友家借书,下图是他离家的距离千米与时间分钟的函数图象,根据图象信息,下列说法正确的是( )
A. 小王去时的速度大于回家的速度
B. 小王在朋友家停留了分钟
C. 小王去时所花的时间少于回家所花的时间
D. 小王去时走上坡路,回家时走下坡路
6.的三个内角::::,则这个三角形是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 等腰三角形
7.下列各式能用平方差公式计算的是( )
A. B.
C. D.
8.如图,≌,若,则的长度为( )
A.
B.
C.
D.
9.如图,直线,,,则( )
A.
B.
C.
D.
10.如图,在锐角三角形中,直线为的中垂线,射线为的角平分线,且直线与射线相交于点若,,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题4分,共24分。
11.计算: ______.
12.如图,是的中线,是边上的中点,连接,若的面积为,则的面积为______.
13.有一棵树苗,刚栽下去时树高为米,以后每年长米,则树高米与年数年之间的关系式为______.
14.如图,把一张长方形纸片沿折叠后,、分别在、的位置上,与的交点为,若,则______.
15.如图,在下列网格中,小正方形的边长均为,点、、都在格点上,则的度数为______.
16.如图,在中,,,线段,的垂直平分线交于点,则的长度为______.
三、解答题:本题共10小题,共80分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算;
化简:.
18.本小题分
计算:先化简,再求值:,其中,.
19.本小题分
如图,、为直角,与相交于点,,求证:推理过程请注明理由
20.本小题分
如图,点、分别在、上,于点,,,求证:.
证明:因为已知,
所以 ______
又因为已知,
所以______同位角相等,两直线平行,
所以______,
所以 ______
又因为 ______平角的定义
所以 ______,
又因为已知,
所以______,
所以______
21.本小题分
甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离开城的距离千米与甲车行驶的时间小时之间的函数关系如图所示,则下列结论:
在上述变化过程中,自变量是______,因变量是______;
,两城相距______千米;
乙车比甲车晚出发______小时,______填甲车或乙车先到达城;
乙车出发______后小时追上甲车;
当甲、乙两车相距千米时,______.
22.本小题分
如图,在长为,宽为的长方形铁片上,挖去长为,宽为的小长方形铁片.
计算剩余部分即阴影部分的面积;
求出当,时的阴影面积.
23.本小题分
如图所示,在正方形网格上有一个.
作关于直线的对称图形不写作法;
在上找一点,使得最小;
若网格上每个小正方形边长为,求的面积.
24.本小题分
如图,已知,点是上一点,.
如图,若,,求证:
;
.
如图,请直接写出与之间满足什么数量关系时,总有成立.
25.本小题分
如图,在中,,,直线经过点,且于点,于点.
当直线绕点旋转到图的位置时求证:≌;;
当直线绕点旋转到图的位置时求证:;
当直线绕点旋转到图的位置时求证:.
26.本小题分
如图,在等边中,边厘米,若动点从点开始,按的路径运动,且速度为厘米秒,设点的运动时间为秒.
当时,判断与的位置关系,并说明理由;
当的面积为面积的一半时,求的值;
另有一点,从点开始,按的路径运动,且速度为厘米秒,若、两点同时出发,当、中有一点到达终点时,另一点也停止运动.当为何值时,直线把的周长分成相等的两部分.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:
;
.
18.解:原式
,
当,时,
原式
.
19.证明:、为直角,
,
在和中,
,
≌,
.
20.证明:因为已知,
所以.
又因为已知,
所以同位角相等,两直线平行,
所以两直线平行,同位角相等,
所以
又因为平角的定义
所以,
又因为已知,
所以同角的余角相等,
所以内错角相等,两直线平行
21.甲车行驶的时间;两车离开城的距离;
;
;乙;
;
或或或.
22.解:根据题意可得,
;
,时,
原式.
23.解:如图所示,即为所求;
连接交于,点即为所求;
.
24.证明:,
,
;
在上截取,连接,如图,
,
,
,
,
,即:,
由知:,
在和中,
,
≌,
;
解:当时,总有成立.理由如下:
如图,在上截取,连接,
在上截取,
,
,
,,,
,
,
,
当时,,
≌,
.
25.证明:,
,而于,于,
,,
,
在和中,
,
≌,
由知≌,
,,
;
,
.
,
≌,
,,
.
,
.
,
≌,
,,
.
26.解:判断:,
理由如下:如图,
,
,
,
;
当的面积为面积的一半时,点为中点或点为中点,则或,
或,
当的面积为面积的一半时,的值为或;
当点在边上,且点在边上时,,
则,
,
当点在边上,且点在边上时,,,
则,
,
所以当为或秒时,直线把的周长分成相等的两部分.
第1页,共1页
同课章节目录
